一道极限题的十一种解法

曾 亮，高德超

（广东理工学院 基础课教学研究部，广东 肇庆 526100）

极限理论是微积分学的理论基础，极限方法是微积分学的基本分析方法[1]，掌握好极限方法对学好微积分具有重要的意义。由于极限方法的多样性和分散性，尤其是0/0型极限，很多学生在初学时感觉不好掌握，所以教师在教学的某个阶段，有必要对该类型极限的常用方法做个总结。笔者在复习和总结0/0型极限的常用方法时，以一道简单极限题为例，给出了十一种解法，串联了所学极限的常用方法，并对使用各种方法的关键点和注意事项做了说明，不仅激发了学生学习极限的兴趣，达到梳理巩固所学知识点的目的，还锻炼了学生的发散思维能力[2]。

下面，先给出一个本文将要用到的结论。

注使用两边夹准则之前，可以通过绘图、取特殊值等方法预先估计所求极限的结果，然后再重点研究放缩技巧。需避免过度放缩，以保证不等式两端的极限值相等。

解法2（利用极限的四则运算法则和第一个重要极限）：

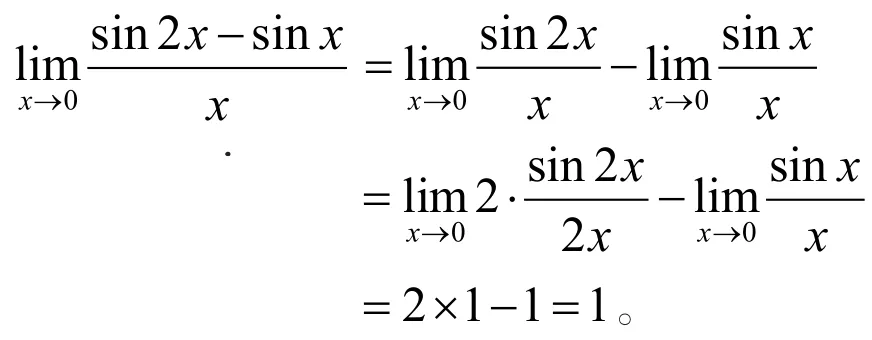
注若将所求极限看作为两函数之和（或差）的极限，则根据极限的四则运算法则，必须要求两函数的极限都存在。

解法3（提取公因式和利用等价无穷小代换）：

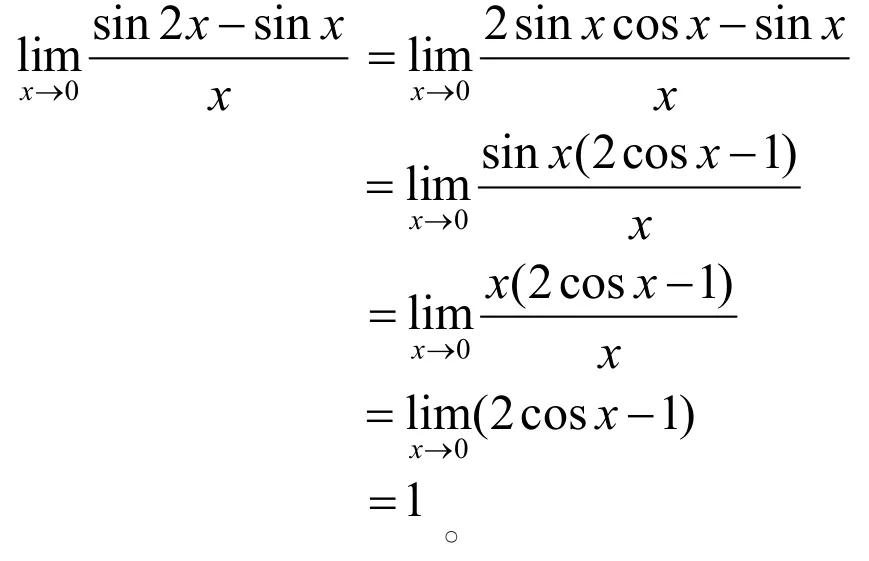
注由于等价无穷小代换一般只能对乘积的因子代换，所以对于函数和差形式可考虑将其化为乘积形式，其中比较常用的方法就是提取公因式。对于此题，除了提取公因式sinx，还可以提取公因式sin2x。

解法4（利用和差化积公式和等价无穷小代换）：

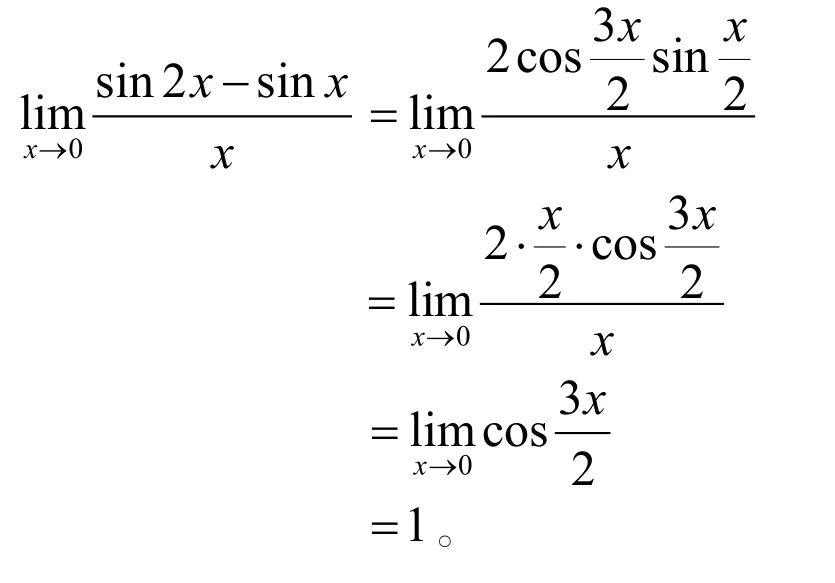
注对于正弦函数或余弦函数的和差形式，若不方便使用提取公因式化乘积形式的方法，还可以利用和差化积公式化为乘积形式。

解法5（利用等价无穷小代换）：

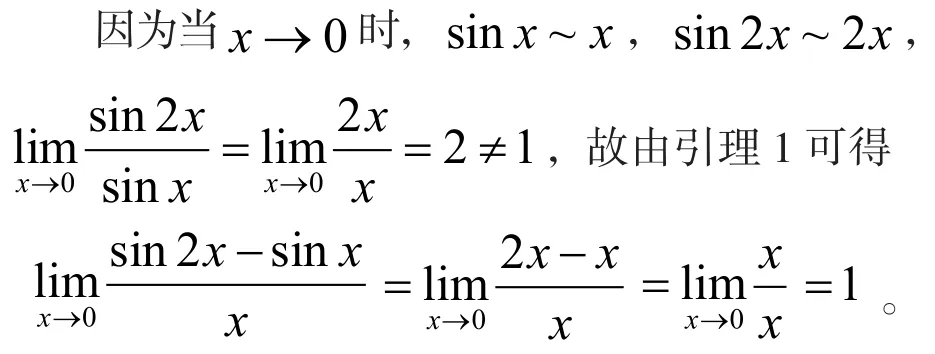
注对于无穷小的和差形式，除了化为乘积形式之外，还可以考虑是否满足引理1的条件。若满足，则可以做整体代换。

解法6（利用泰勒公式）：

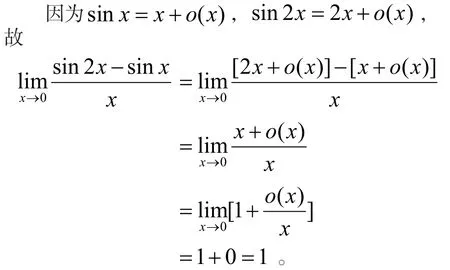
注当函数和差形式不能直接利用或不方便利用等价无穷小代换时，可以考虑利用泰勒公式展开，阶数的展开应遵循“上下同阶”原则和“幂次最低”原则[4]。

解法7（利用导数的定义）：

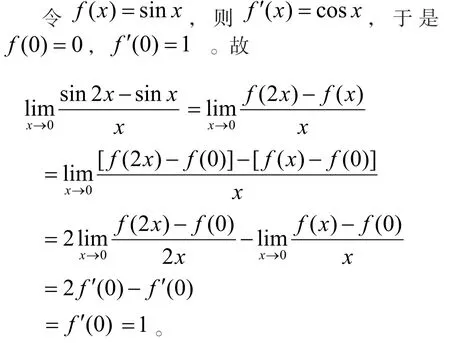
注当极限表达式容易变形为某函数的增量与自变量的增量的比值时，则可以考虑利用导数的定义计算所求极限。

解法8（利用洛必达法则）：

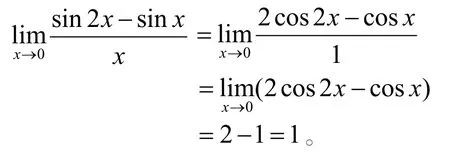
注利用洛必达法则之前，必须判别所求极限是否满足洛必达法则的使用条件。

解法9（利用拉格朗日中值定理）：

令f(t)=sint，显然f(t)在闭区间[x,2x]（或[2x,x]）上连续，在开区间(x,2x)（或(2x,x)）内可导，且计算有f′(t)=cost.由拉格朗日中值定理得：

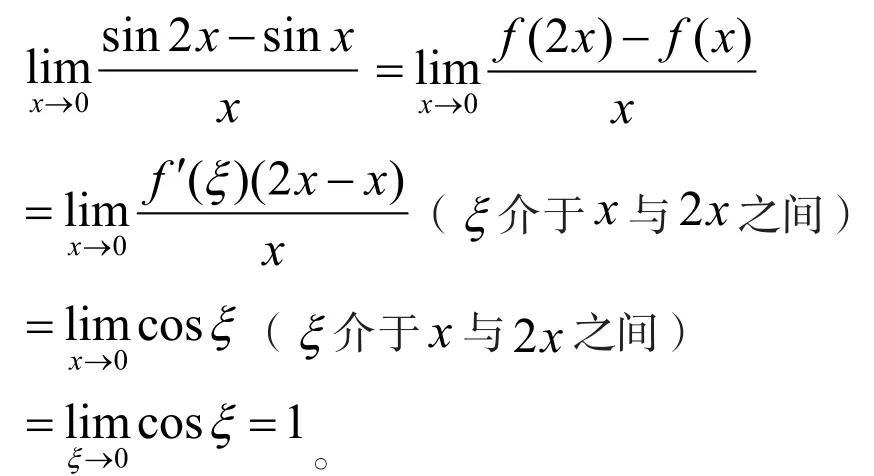
注当极限表达式的分子或分母为两同类函数之差的形式时，可以考虑利用拉格朗日中值定理求极限。

解法10（利用柯西中值定理）：

令f(t)=sint，g(t)=t，则f′(t)=costg′(t)=1.显然f(t)和g(t)在闭区间[x,2x]（或，[2x,x]）上连续，在开区间(x,2x)（或(2x,x)）内可导，且g′(t)在(x,2x)（或(2x,x)）内每一点处均不为零，则由柯西中值定理可得：

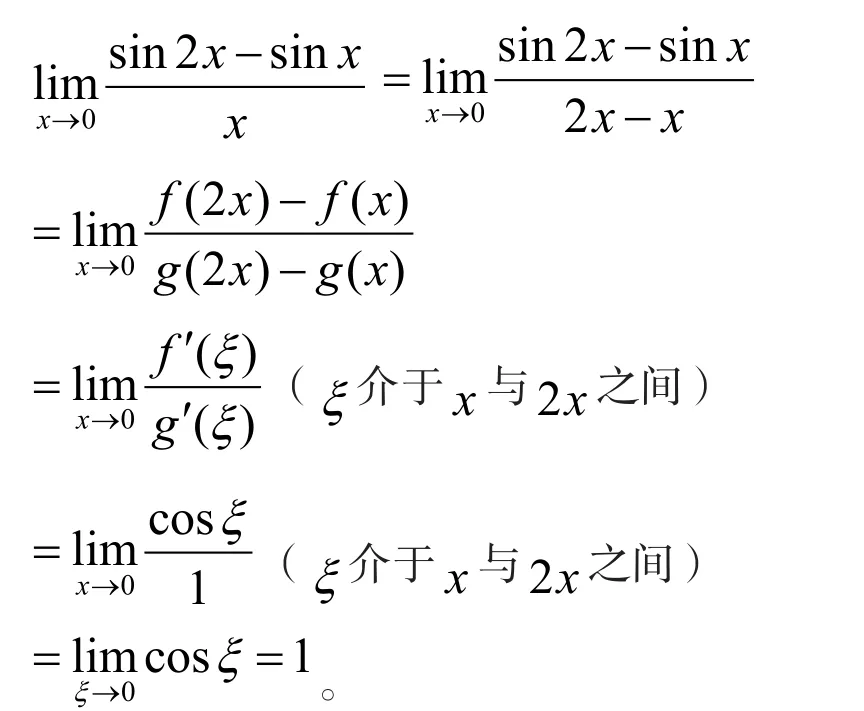
注柯西中值定理是拉格朗日中值定理的推广，当极限表达式的分子和分母都可以表示为两同类函数之差的形式且使用拉格朗日中值定理失效时，可考虑使用柯西中值定理。

解法11（利用积分中值定理）：

注对表达式含有积分的极限，可利用积分中值定理将其转化为一般的极限（不含积分），再利用其他方法求解，但要注意中值点在所在区间的任意性。

针对极限方法的多样性，无论教师在教学中还是学生在平时学习中，应挖掘好题，注重一题多解，有助于打破思维定势，提升学生运用数学知识的能力和发散思维能力，这样在面对各种极限题时，总能找到最合适的求解方法。