基于遗传算法和免疫算法的垃圾清运路径规划
——以安阳工学院为例
2022-04-15李亚茹
李 航,刘 然,张 洁,李亚茹
(安阳工学院,河南 安阳 455000)
随着垃圾分类的力度日益加大,高校为了满足垃圾收集,在校园内投放了大量的垃圾桶,但是垃圾回收车的路径常为随机运动,这使得运输产生了较多的往复,增加了运输时间和成本,一些研究运用蚁群算法进行路径优化[1-8],一些则采用遗传算法将之转变为TSP问题求解[9-15]。实际垃圾收运问题涉及回收中心、车辆装载、往复运输等约束条件,因此垃圾收运可以化归为CVRP问题,垃圾中转站设置可以化归为FLP问题,为了更加有效的设置中转站并调动垃圾车清运,采用GA算法和IA算法进行优化设计。
1 垃圾运输问题提出及其数学模型
安阳工学院校园内现有垃圾回收点77处,垃圾中转站1处,垃圾回收车7辆,每辆垃圾回收车最大载量为400 L,每次全园区清运总费用约1 150元,在无时间窗限制的情况下,垃圾回收车均以空车状态从垃圾中转站出发,遍历77处垃圾回收点,当回收达到最大载量后需要回到中转站卸载而后再投入工作,直至所有垃圾清运完成,其数学模型可以描述为:园区内有1处垃圾中转站,中转站有m辆垃圾回收车,记为V={k},k=1,2,……m,每辆垃圾回收车载重为L,站点集合记为P={i},i=1,2,……n,各站点垃圾数量为Qi,从站点i到j的路程记为Dij,Cij为收运成本,规划收运路线最短,分配垃圾回收车数量m最少。
目标函数如下式所示:

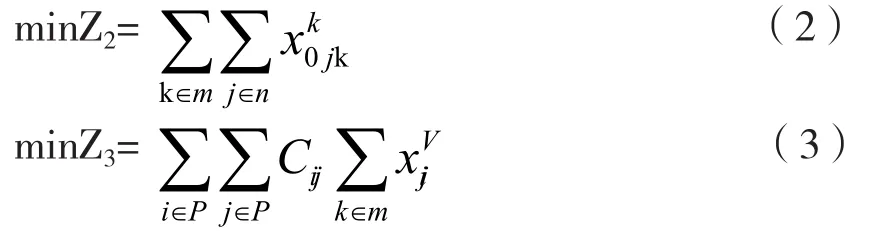
约束条件如下式所示:
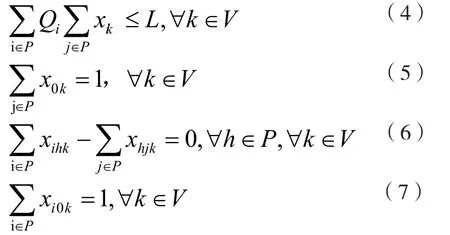
其中,式(1)表示垃圾回收车行程最短;式(2)表示垃圾回收车数量使用数最少;式(3)表示最小清运成本;式(4)表示垃圾回收车不能超载;式(5)、式(6)、式(7)表示垃圾回收车从垃圾中转站0出发,如果某处垃圾站点已经被回收则其他垃圾车不再处理,回收完成后所有垃圾回收车最终返回中转站。
实际案例中垃圾回收点和垃圾中转站散点图如图1所示,网格单位为米。

图1 垃圾回收点和垃圾中转站散点图
2 遗传算法求解
2.1 编码
对于n个目标点的CVRP问题使用自然数编码,即坐标系内各点用自然数(n≥1)标记,本例中中转站数量为1,编号标记为0,各垃圾回收点从1开始标记,受载重的约束,垃圾回收车ki从0开始收运并累积每个回收点的垃圾数量,超过最大载量时返回0点,并继续遍历,直到园区内垃圾均回收。
2.2 种群初始化
根据目标点规模数量初始化一个种群作为初始解,本例采用随机生成法,取值50。
2.3 适应度函数
将P1|P2|P3|……|Pn|作为一个采用自然数编码的染色体,为回收点Pi到Pj的距离,个体适应度Fitness可表述为

即遍历n个回收点再返回0点路程的倒数,适应度函数的值越大染色体表现越好,反之则越差。
2.4 遗传算子
个体被选中的概率与其适应度函数成正比,数量为n群体中,个体i被选中遗传到下一代的概率Si的可表述为式(9),在遗传算子的基础上,采用轮盘赌算法确定个体是否被遗传到下一代。

2.5 交叉运算
采用部分映射多点杂交,产生个数为Nu的随机数,则父代个体基因串被分成Nu个基因段,A(i)表示父代个体A的第i个基因段,Ai=1……Nu,交叉概率取0.9。
2.6 变异运算
采用基本位变异,变异概率设定为0.05,即种群内所有基因的5%进行变异,迭代数为100。
遗传算法初始相关参数如表1。

表1 遗传算法初始参数
2.7 优化结果
本例中仅存在一个垃圾中转站,5辆垃圾回收车即可完成整个园区的清运工作,较当前设置可以节省2辆垃圾回收车,5辆垃圾回收车总路程为5 986.84 m,路径图及清运总成本变化趋势如图2所示,清运路径如表2所示,回收成本降到600元左右,降比约48%。

表2 遗传算法路径表

图2 中转站数=1时清运路径优化图及总成本变化趋势图
分析优化结果可知,路线5仅经过了5个回收点,且与多条路径之间产生交叉点,导致清运线程增加。在该模式下,处于园区边缘的回收点垃圾存放量较少,垃圾回收车仅需访问1次即可完成该点清运,因此Pc=0.9时,模型趋向纯粹随机搜索,遗传算法结果的收敛性较差,重新设置Pc=0.5,Pm=0.01,并增加迭代次数为200,优化清运路线及总成本变化趋势如图3所示,5辆垃圾回收车路径如表3,总路程5 853.33 m,回收成本为595元。

表3 Pc=0.5、MAXGEN=200路径表
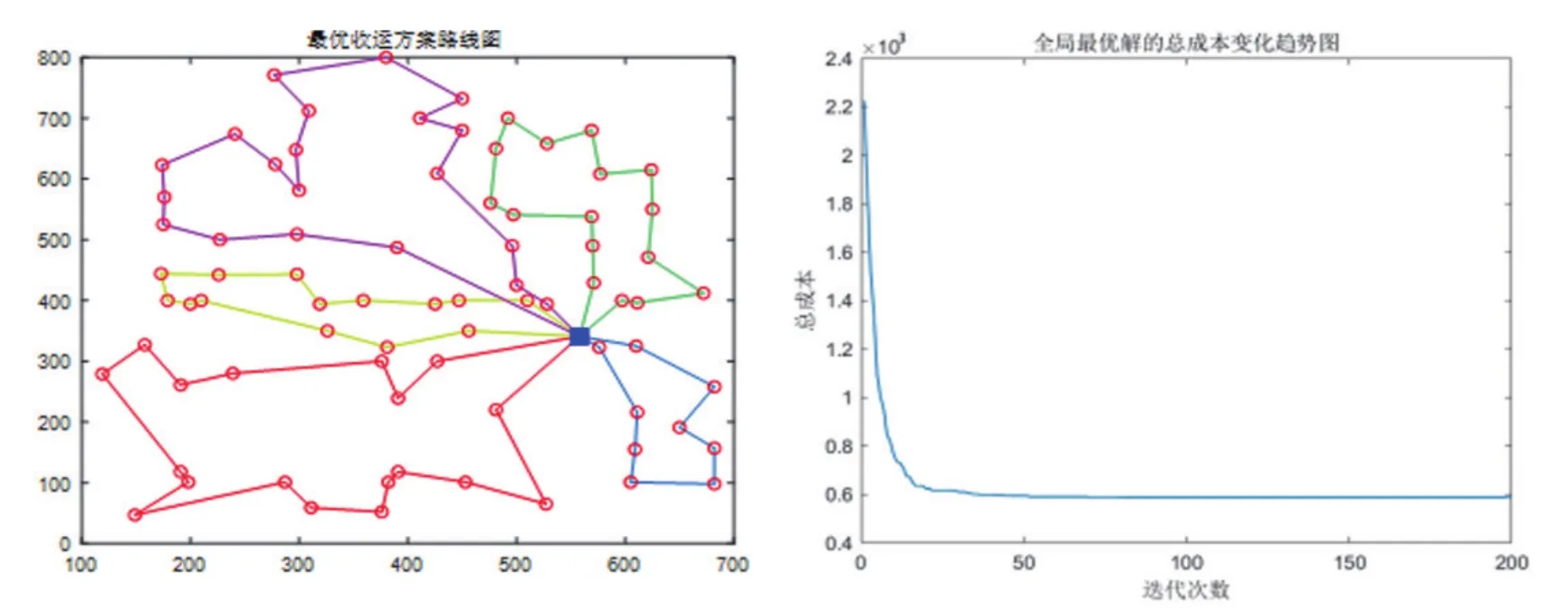
图3 Pc=0.5、MAXGEN=200路径优化路线图及总成本变化趋势图
3 选址问题的提出及其数学模型
由上述遗传算法结果可知,1处垃圾中转站无法保证垃圾回收车就近卸载,实际上延长了清运路线,适当增加中转站数量并求解其位置可以进一步减少清运路线和清运成本。此处选择使用免疫算法对多基址选取进行模拟优化[16-22],在遗传算法得出5辆垃圾回收车的前提下,其数学模型可以描述为:园区内有大于1处的垃圾中转站,记为Hi,所有中转站共有5辆垃圾回收车,记为V={k},k=1,2,……5,每辆垃圾回收车载重为L,垃圾站点集合记为P={i},i=1,2,……n,各站点垃圾数量为Qi,从垃圾回收站点i到垃圾中转站j的路程记为dij,垃圾中转站距离由其服务的垃圾回收车的距离上限记为S,到回收点i的清运距离小于S的备选中转站集合记为Mi,垃圾回收站点与垃圾中转站的分配关系记为Jij,该值为0-1变量,Jij=1表示回收站点与垃圾中转站j匹配,否则Jij=0,点j是否选为垃圾中转站由0-1变量表示,记为hi,hj=1表示选为中转站,否则hj=0,综上在满足距离上限的前提下,从所有回收点找出中转站并回收垃圾,目标函数是各中转站到回收站点的清运量和清运距离的乘积之和最小。
目标函数如式(10)所示:

约束条件如式(11)-式(15)所示:

式中,式(10)表示垃圾回收站点到垃圾中转站距离乘积之和最小;式(11)表示5辆垃圾回收车只能由一个垃圾中转站发出;式(12)表示没有中转站则不会接受垃圾回收车返程卸载;式(13)表示垃圾中转站总数量;式(14)表示Jij和hj两个变量;式(15)表示垃圾回收站点与垃圾中转站距离未超过上限值。
4 免疫算法求解
4.1 初始化记忆库
设置非空记忆库,保证初始抗体群从记忆库中产生,每个选址方案形成一个长度为t的抗体(t表示垃圾中转站数量),每个抗体表示被选为中转站的序列,本例中t=3,记忆库容量=20。
4.2 多样性评价参数
多样性评价由抗体与抗原间的亲和力、抗体与抗体间的亲和力、抗体浓度以及繁殖概率得出,本例中采用精英保留策略,每次更新记忆库均先将与抗原亲和度最高的个体存入记忆库,针对垃圾中转站选址模型,设定多样性评价参数Ps=0.9。
4.3 免疫操作
采用轮盘赌算法选择单点交叉机制以及随机变异,得交叉概率Pc=0.8,变异概率Pm=0.01,迭代次数为200,垃圾中转站数为2。
免疫算法初始相关参数如表4。

表4 遗传算法初始参数
4.4 优化结果
将垃圾中转站数量分别设定为2个、3个、4个、5个,选址位置及收敛曲线如图4所示。本例中,当垃圾中转站数量超过3个后,垃圾回收车及中转站利用率迅速降低,因此,综合评价园区内可设置垃圾中转站数量为3,其坐标分别为A[191,261],B[381,323],C[527,65],对应垃圾回收点数量分别为16,48,13。

图4 垃圾中转站数量分别为2、3、4、5时选址位置图及收敛曲线图
以3个垃圾中转站再次进行遗传算法路径优化,路径图和总成本图如图5所示,5个垃圾回收车的清运总路径为5 326.94 m,清运成本约为502元,较“2.7”环节计算结果总路径进一步减少550 m,清运成本降低约90元,分析变化趋势图可以发现曲线有较大波动但是收敛效果较佳。
图5 中转站数=3时清运路径图及总成本变化趋势图
5 结论
以安阳工学院为例研究了垃圾中转站设置和垃圾清运路线,得出校园内站点分布相对集中、中转站数量相对较少,不同分区内垃圾数量的差异较大,处于边缘的垃圾回收站点通常仅需一次访问,在没有时间窗限制的条件下,垃圾回收车路径优化主要由交叉概率Pc、变异概率Pm两个参数控制,当Pc=0.5和Pm=0.01时收敛平稳的结论。
园区内当前仅有一个垃圾中转站,本研究增加了边缘垃圾中转站的访问路径,根据免疫算法将园区内中转站设定为3个,可以在现有垃圾回收点不变的情况下,进一步优化清运路径及降低费用。
