拉格朗日中值定理的10个推广

(玉溪师范学院 数学与信息技术学院,云南 玉溪 653100)

拉格朗日中值定理是数学分析中很重要的定理，同时在高等数学中也占有重要的地位，它可以研究函数在整个区间的整体性.在各类大型考试中，拉格朗日中值定理也占有很重要的位置，是主要的考点，经常会出现在一些理论分析和证明题中.本文主要阐述拉格朗日中值定理在实函数论中的推广，通过这些推广可以拓宽拉格朗日中值定理的使用范围.

本文探究了拉格朗日中值定理的10个推广，并根据拉格朗日中值定理的推广来解决实际问题.总体看,不同的推广有不同的特点，且每个推广与拉格朗日中值定理之间是相互联系的.

1 拉格朗日中值定理

下面介绍本文涉及的定理：

定理(拉格朗日中值定理) 若函数f(x)满足：

(1)在闭区间[a,b]上连续；

(2)f(x)在开区间(a,b)内可导.

则在开区间(a,b)内至少存在一点ξ，使得

显然，当f(a)=f(b)时，拉格朗日中值定理就是罗尔中值定理.

这表明罗尔中值定理是拉格朗日中值定理的一个特殊情况.

2 拉格朗日中值定理的推广

定理1 设函数f(x),g(x)在[a,b]上连续，在(a,b)内可导，则至少存在一点ξ∈(a,b)，使得

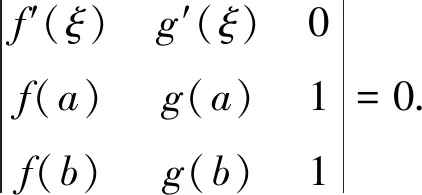
因为f(x)在[a,b]上连续，在(a,b)内可导，且F(a)=F(b)=0，

则由罗尔中值定理可得，存在一点ξ∈(a,b)，使得F′(ξ)=0.即

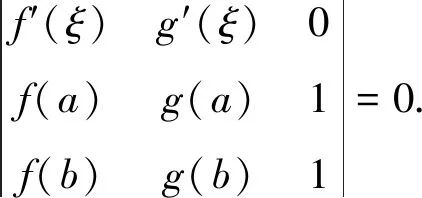
定理2 设函数f1(x),f2(x),…,fn(x)在[a,b]上连续，在(a,b)内可导，存在一点ξ∈(a,b)，使得

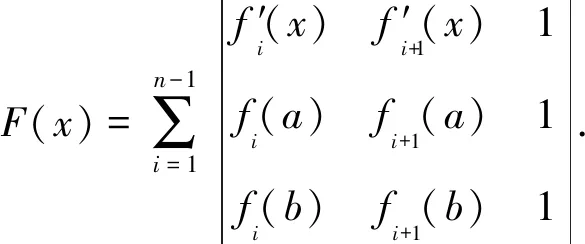
因为F(x)在[a,b]上连续，在(a,b)内可导，且F(a)=F(b)=o，

则由罗尔中值定理可得，存在一点ξ∈(a,b)，使得F′(x)=0.即

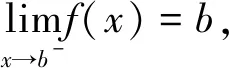
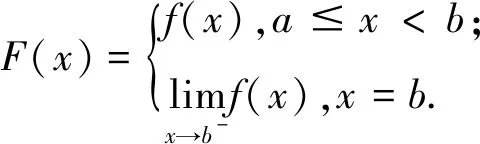
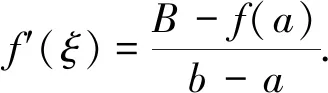
类似可证：

类此可证：

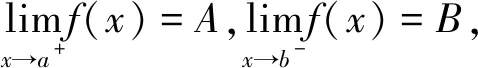
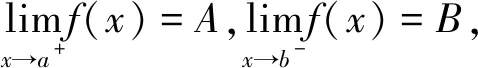
证明设f(x)仅在c∈(a,b)不可微，则由拉格朗日中值定理可得，存在ξ1∈(a,c)，ξ2∈(c,b),其中，ξ∈(a,b)，使得

f(c)-A=f′(ξ1)(c-a)，ξ1∈(a,c)，

B-f(c)=f′(ξ2)(b-c)，ξ2∈(c,b).

令，|f′(ξ)|=max{|f′(ξ1)|,|f′(ξ2)|}则

|B-A|≤|f′(ξ)|(b-a).

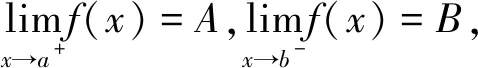
证明设f(x)仅在c∈(a,b)内不可微，则由拉格朗日中值定理可得，存在ξ1∈(a,c)，ξ2∈(c,b),其中，ξ∈(a,b)，使得

f(c)-A=f′(ξ1)(c-a)，ξ1∈(a,c)，

B-f(c)=f′(ξ2)(b-c)，ξ2∈(c,b),

取实数α1,α2，使得α1(b-a)=c-a，α2(b-a)=b-c,则α1+α2=1,α1>0,α2>0，且

B-A=[α1f′(ξ1)+α2f′(ξ2)](b-a).

定理7 设函数f(x)在[a,b]上连续，在(a,b)内存在右导数f′+(x)，当f(a)>f(b)(或f(a)

证明存在m，使得f(a)>m>f(b).

令E={x|f(x)

在c的领域内，当a

同理可证：

推论2 设函数f(x)在[a,b]上连续，且在(a,b)内存在左导数f′-(x)，当f(a)f(b))时，则存在一点c∈(a,b)，使得f′-(c)≥0(或f′-(c)≤0).

定理8 设函数f(x)在[a,b]上连续，在(a,b)内存在右导数f′+(x)，且f(a)=f(b)，则存在x1,x2∈(a,b)，使得f′+(x1)≤0,f′+(x2)≥0.

证明①若f(x)=f(a)，则对任意的x1，有

所以f′+(x1)=0，结论成立.

②若f(x)≠f(a)，则存在一点c∈(a,b)，使得f(c)>f(a)；或存在一点d∈(a,b)，使得f(d)

由定理7可得，存在x1,x2，且a

f′+(x1)≤0,f′+(x2)≥0.

同理可证：

推论3 设函数f(x)在[a,b]上连续，在(a,b)内存在左导数f′-(x)，且f(a)=f(b)，则存在x1,x2∈(a,b)，使得f′-(x1)≤0,f′-(x2)≥0.

对F(x)求右导数，得:

因为函数F(x)在区间[a,b]上连续，在(a,b)内存在f′+(x)，且F(a)=F(b)=0.

由定理7可得，存在x1,x2∈(a,b)，使得F′+(x1)≤0,F′+(x2)≥0.即

推论4 设函数f(x)在[a,b]上连续，且在(a,b)内存在左导数f′-(x1)，则存在x1,x2∈(a,b)，使

定理10 设函数f(x),g(x)在(a,b)内存在右导数f′+(x),g′+(x)，且f(x),g(x)在[a,b]上连续，则存在x1,x2∈(a,b)，使

(f(b)-f(a))g′+(x1)-(g(b)-g(a))f′+(x1)≤0，

(f(b)-f(a))g′+(x2)-(g(b)-g(a))f′+(x2)≥0.

对F(x)求右导数，得:

F′+(x)=(f(b)-f(a))g′+(x)-(g(b)-g(a))f′+(x).

因为F(x)在[a,b]上连续，F′+(x)在(a,b)内存在，且F(a)=F(b)=0.

由定理7可得，存在x1,x2∈(a,b)，使得F′+(x1)≤0,F′+(x2)≥0.所以有，

(f(b)-f(a))g′+(x1)-(g(b)-g(a))f′+(x1)≤0，

(f(b)-f(a))g′+(x2)-(g(b)-g(a))f′+(x2)≥0.

推论5 设函数f(x),g(x)在(a,b)内存在f′-(x),g′-(x)，且f(x),g(x)在[a,b]上连续，则存在x1,x2∈(a,b)，使

(f(b)-f(a))g′-(x1)-(g(b)-g(a))f′-(x1)≤0，

(f(b)-f(a))g′-(x2)-(g(b)-g(a))f′-(x2)≥0.