稳健ARMA 残差控制图的构建及在金融市场的应用

黄水仁 刘玉记 胡杰

(广东财经大学统计与数学学院,广州,510320)

1 引言

在统计过程控制中,传统控制图的基本假设是要求数据服从独立同分布.但是在大数据时代背景下,数据的性质和分布变得更加复杂,导致受控过程违背了独立同分布的基本假设.特别是金融数据,它们的自相关性以及异方差性会表现得更加明显.数据的这些特征会导致常规控制图监控失效，使得监控结果与实际情况存在偏差，导致控制图出现错报和漏报的概率增大.

国内外有不少专家学者对这一问题进行深入探讨.对于存在自相关性的数据目前比较流行的是Alwan[1]提出的残差控制图方法,国内学者孙静[2]、张志雷[3]、范翔[4]和肖艳[5]等也对这一问题进行了研究,他们将呈现自相关过程的监控问题转化为相应的残差的监控,从而用自回归移动平均(Auto-Regressive Moving Average,ARMA)模型来拟合自相关过程,得到相应的残差序列;对于具有异方差性的数据,目前最流行的是Severin 和Schmid[6]、夏远强[7]、Sermad 和Roland[8]等学者提出的用波动的上、下控制限替代固定的上、下控制限来构建控制图的方法; 对于自相关性和异方差性并存的数据,王志坚[9]、李雄英[10]等分别提出用ARMA-GARCH 型残差控制图和ARMA-TGARCH 型残差控制图对受控过程进行监控.但是在金融市场上,由于数据量庞大,离群值通常会很多,若采用迭代的自适应微调法,先识别超出均值控制限的点,再对它们进行删除处理会存在一定的困难,特别是传统残差控制图对离群值非常敏感.因此当使用ARMA 残差控制图对数据进行分析时需要一个新算法,这个算法既要考虑到如何消除或者降低离群值的影响,又要尽可能提供避免逐一识别离群值的这个功能.这就需要一种稳健、高抗差性的方法来检测样本中的离群值,使其结果比较合理地反映事实.

比较成熟的稳健统计的估计量是由Huber 提出的,它能在满足经典假设的条件下获得优良的结果,甚至在某些假设条件不能满足的情况下,也只是受到轻微的影响.Huber[11-13],Maronna[14]以及Roussrruw[15]等学者把稳健估计量扩展为除了能反映大多数样本数据的特征不受离群值干扰之外，还能把样本中的离群值检测出来.国内外也有专家学者使用稳健统计的思想对传统方法进行改进.Yang 和Su[16]、仲建兰[17]、王斌会[18]、刘晓华[19]以及宋鹏[20]等分别使用可变抽样区间、Fast-MCD、异方差和中心正则化等稳健统计量对传统马尔可夫链、传统因子分析方法、传统ARCH 模型和传统样本协方差矩阵估计等方法进行稳健性改进,并且构建出稳健模型分析算法.研究结果均表明当数据中存在离群值时,稳健估计算法比传统方法具有更高的抗差性和抗干扰性,这些研究为本文的方法构建提供了有益的基础和借鉴.

2 传统ARMA 控制图的原理及其不稳健性

2.1 传统ARMA 控制图的原理

设受控的ARMA(p,q)过程为:

其中,γ(0)为受控过程Xt的方差,ρ(k)∈(-1,1).

定义统计量Zt如下:

其中φ表示回归系数,θ表示平均偏移系数,且α=1-φ+θ.经过迭代后,有

其中,β=φα-θ.Zt的协方差为:

当k=0 时,得到Zt的方差

由Zt的均值和标准差可得到传统ARMA 控制图的上控制限(UCL)、中心线(CL)以及下控制限(LCL):

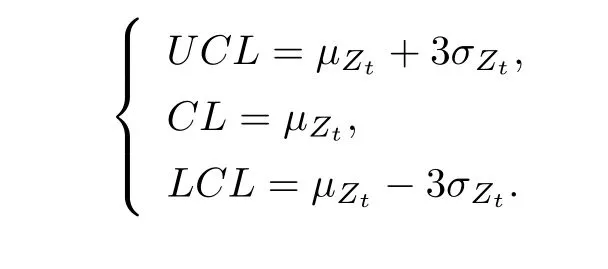
2.2 传统ARMA 控制图的不稳健性

在传统ARMA 模型中,受控过程的自相关函数和偏自相关函数是由其样本自协方差函数得到的,而这两个统计量都对离群值比较敏感,有时仅仅一个离群值就可能使得计算结果与实际情况偏离较远.为了说明离群值的存在可能会影响传统ARMA 控制图的计算结果,本文使用R 软件模拟出一组样本量为50 且服从标准正态分布的随机数(称为数据组1),构造两个离群值-3.50 和3.50,分别代替数据组1 中的第24 号和26 号样本值,得到的新数据组称为数据组2,详见表1.

表1 数据组1 和数据组2

根据表1 的两组数据,利用传统ARMA 方法绘制出各自的控制图,结果见图1,其中“虚线”表示不存在离群值时传统ARMA 控制图的控制限,“实线”表示存在离群值时传统ARMA 控制图的控制限;“实心点”代表正常值,“空心点”代表离群值.

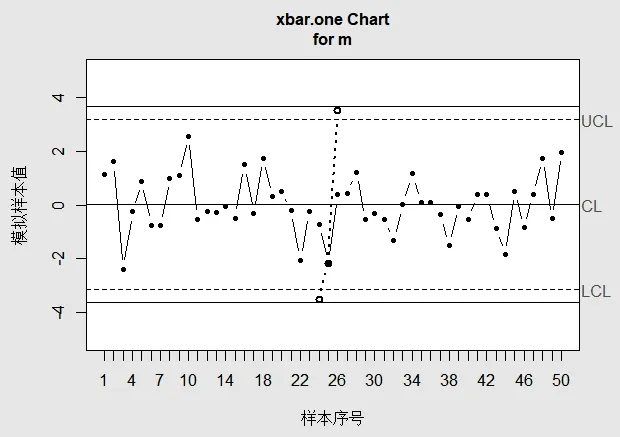
图1 不存在离群值和存在离群值的传统ARMA 控制图

由图1 可知,当数据中不存在离群值时,传统ARMA 控制图的上、下控制限分别为-3.15 和3.16;当数据中存在少量离群值时,传统ARMA 控制图的上、下控制限发生了变化,变为-3.64 和3.67,此时传统ARMA 控制图并不能识别出第24 和26 号离群值,即出现了漏发报警的现象.这是因为当数据中存在离群值时,传统ARMA 控制图的控制限被拉大,导致离群值没有被检测到,以至于出现了漏发报警的现象.这说明统计量的不稳健性会直接导致传统ARMA 控制图的监控结果与实际情况产生偏差,因此,在相关的模型中需要运用稳健统计方法来对其进行改进.

3 稳健ARMA 残差控制图的构建

本文通过借鉴Huber 的M 估计基本理论,采用Hampel 权函数对原序列进行变换,再对变换后得到的新序列进行建模,得到稳健的ARMA 控制图模型.

Hampel 权函数的表达式如下:

其中,a,b,c的值可以取任意大于0 的实数,这里参考文献[9],分别取值1.5,3.0,4.5.当残差绝对值小于aσ时,权重赋值为1,观测的序列取原序列;当残差绝对值大于或等于aσ而小于bσ时,权重赋值为aσ/|εi|;当残差绝对值大于或等于bσ而小于cσ时,权重赋值为(a/|εi|)(cσ-|εi|)/(c-b),由此可知,权重随着残差绝对值的增大而逐渐减小;当残差绝对值大于或等于cσ时,权重赋值为0,即该部分的观测值不予采用.

稳健的样本自协方差可表示为:

其中,ω为Hampel 权函数,εt为序列Xt的残差.通过Hampel 权函数对原序列有差异性地赋予权重,有效地减轻了离群值带来的影响,较大地提高了监测的准确性.

本文根据加权后的稳健样本自相关函数和偏自相关函数的特点来选择ARMA 模型的类型,确定模型的阶数,从而构建出稳健的ARMA 控制图,其上控制限(UCL)、中心线(CL)和下控制限(LCL)分别为:

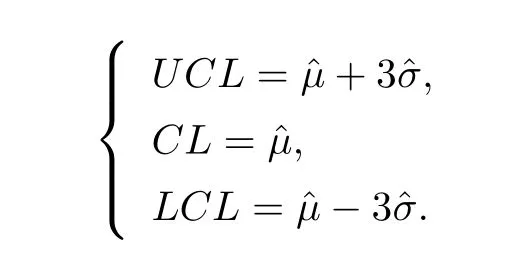
由于残差控制图的中心线和上、下控制限均是波动的,经过对样本自协方差、均值和标准差的稳健改进,得到稳健样本自协方差ˆγ(k)、稳健均值ˆμ和稳健标准差ˆσ,从而增强ARMA 残差控制图对离群值的识别能力,降低其漏报或者虚报的概率.

4 模拟实验

为了比较传统ARMA 残差控制图和稳健ARMA 残差控制图对离群值的识别能力,本文对服从ARMA(1,1)模型的受控过程抽取容量为300 的样本,并由此分别构造离群率为ε=0,ε=5%,ε=10%和ε=15%的序列.离群率ε=0(即序列中不含离群值)的序列即为原序列; 当离群率ε=5%时,数据序列中含有15 个离群值,依此类推.

下面分别是离群率ε=0,5%,10%和15%的序列图(见图2 和图3).

图2 不含离群值和含5%离群值的序列图

图3 含10%离群值和15%离群值的序列图

对含有不同比例离群值的序列分别建立传统的和稳健的时间序列ARMA 模型,结果见表2.

表2 含不同比例离群值时传统和稳健ARMA 模型系数的比较

从表2 可知,当数据中含不同比例的离群值时,传统ARMA 模型的系数变化较稳健ARMA 模型的系数变化偏大,说明传统ARMA 模型容易受到离群值的影响,而稳健ARMA 模型较稳定,受离群值的影响程度较小.因此,稳健ARMA 模型对离群值具有一定的抗差性和抗干扰性.

为了进一步考察稳健ARMA 模型在含有不同比例离群值的序列上的表现,下面分别根据传统与稳健ARMA 模型所得到的自相关序列构建残差控制图,比较其对离群值的检测效果.

对不含离群值的序列,比较结果如图4 所示(“虚线”表示传统ARMA 残差控制图的上、下控制限,“实线”表示稳健ARMA 残差控制图的上、下控制限,下同).由图4 可知,当数据中不存在离群值时,传统ARMA 残差控制图的上、下控制限分别是-3.0007 和3.217;稳健ARMA 残差控制图的上、下控制限分别是-2.874 和3.13,两者的控制限几乎重合.

当数据中含有10%,即30 个离群值时,图5 显示,传统ARMA 残差控制图识别出了22 个离群值,正确报警率约为73.3%,漏报警率约为26.7%;而稳健ARMA 残差控制图识别出了29 个离群值,正确报警率达到了96.7%,稳健效果达到了较佳的状态.

当数据中含有15%,即45 个离群值时,图6 显示,传统ARMA 残差控制图识别出了16 个离群值,正确报警率约为35.6%,漏报警率约为64.4%;而稳健ARMA 残差控制图识别出了43 个离群值,正确报警率达到了95.6%,且传统ARMA 残差控制图能识别出来的离群值,稳健ARMA 残差控制图均能识别出来,说明相对传统ARMA 残差控制图,稳健ARMA 残差控制图受离群值的影响程度较小,对离群值具有一定的抗干扰能力.

综上,随着数据中所含离群值数量的不断增加,传统ARMA 残差控制图受离群值的影响程度越来越明显,漏发报警率越来越高;而稳健ARMA 残差控制图比较稳定,受离群值的影响不明显,对离群值的识别程度还是很高,且传统ARMA 残差控制图能识别出来的离群值,稳健ARMA 残差控制图均能识别出来.相反地,稳健ARMA 残差控制图能识别出来的离群值,传统ARMA 残差控制图不一定能识别出来,这说明稳健ARMA 残差控制图对离群值的抗干扰性较强.

图4 不含离群值时传统与稳健ARMA 模型的残差控制图

图5 含10%离群值的传统与稳健ARMA 残差控制图

图6 含15%离群值的传统与稳健ARMA 残差控制图

5 实证分析

为了比较稳健ARMA 残差控制图与传统ARMA 残差控制图在实际应用中对离群值的监控效果,本节选取搜狐(SOHU)公司2018 年7 月2 日至2020 年6 月30 日的502 个股票收盘价为样本数据(数据来源于雅虎财经).由于2018 年7 月4 日美国金融市场休市,7 月30 日受美股涨跌影响,搜狐股价大跌超20%,而2020 年中国受新冠疫情影响,搜狐的股价又出现大跌,所以该股票数据中存在一定数量的离群值,这与本文的研究目标相吻合.

我们采用差分法将搜狐股票的收盘价数据转化为对数收益率数据rt,分别作出该样本数据的对数收益率图和直方图,见图7.

从图7 可初步判断数据中可能存在离群值.为了进一步判断离群值的存在是否会导致数据偏离正态分布,我们对rt进行Jarque Bera 检验.检验结果显示P-value＜2.2e-16,说明搜狐的收益率序列不服从正态分布,即收益率序列中含有离群值.

然后对搜狐的对数收益率序列进行ADF 检验,结果显示P-value 是0.01,说明有99%的把握拒绝收益率序列中存在单位根,这表明搜狐的收益率序列是平稳的.对收益率序列构建ACF 和PACF图(见图8 和9),经过多次试验比较,最终确定传统ARMA(p,q)模型中的p=1,q=1 时为最优.

图7 搜狐样本数据的对数收益率图(左)和直方图(右)

图8 搜狐收益率序列ACF 图

接着对传统ARMA(1,1)模型的参数进行估计,结果如表3 所示:

表3 传统ARMA(1,1)模型的参数估计结果

由表3 显示的结果可得到如下的传统ARMA(1,1)模型:

根据此模型可得到对数收益率的残差序列,然后计算残差序列的均值和标准差,即可构建出传统ARMA 模型的残差控制图,如图10 所示.

由图10 可知,传统ARMA 残差控制图的上、下控制限分别为-0.13 和0.13.传统方法识别出了6 个离群值,分别是第18,205,273,427,429 和450 号样本.

接下来使用稳健统计方法将对数收益率的残差序列进行稳健处理.根据AIC 原则,可建立稳健ARMA(2,2)模型,其参数估计结果如表4 所示.

表4 稳健ARMA(2,2)模型的参数估计结果

由表4 的结果可得到如下的稳健ARMA(2,2)模型:

利用此模型构建出稳健ARMA 残差控制图,并将其与传统ARMA 残差控制图进行比较,结果如图11 所示(图中,虚线表示传统ARMA 残差控制图的上、下控制限,实线表示稳健ARMA 残差控制图的上、下控制限).

由图10 可知,由传统ARMA 模型构建的残差控制图只能识别出6 个离群值.这是由于离群值的存在,使得传统ARMA 残差控制图的控制限被拉高了,才导致某些离群值没有被检测出来;而稳健ARMA 残差控制图的上、下控制限分别约为-0.0882 和0.0876,稳健ARMA 残差控制图能识别出18 个离群值(见表5).

表5 识别的离群值序号

由表5 可知,传统ARMA 残差控制图能识别出来的离群值,稳健ARMA 残差控制图也能识别出来,而稳健ARMA 残差控制图能识别出来的离群值,传统ARMA 残差控制图不一定能识别出来.可见,稳健ARMA 模型的残差控制图对离群值有着较好的抗御能力.

综合上节模拟实验和本节实证研究得到的结果可知,传统ARMA 残差控制图易受离群值的影响,导致控制限被拉高,从而出现漏发报警的缺点;而本文构建的稳健ARMA 残差控制图不仅对离群值具有较好的抗干扰性,而且其控制限和控制中心不易受离群值的影响,能够较好地监测到离群值的位置,并正确地发出警报.特别是,稳健ARMA 残差控制图能较好地处理金融市场中呈自相关的股票数据的监控问题,能给投资者提供有益的决策信息,有较好的实际意义.

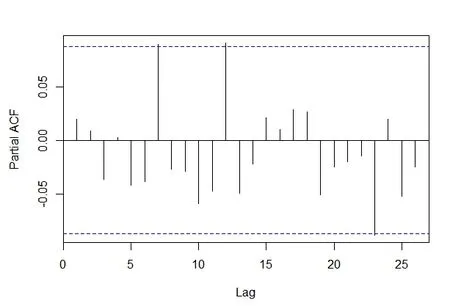
图9 搜狐收益率序列PACF 图

图10 搜狐股价对数收益率的传统ARMA 残差控制图

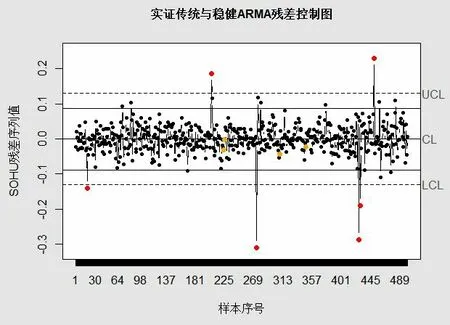
图11 传统和稳健ARMA 残差控制图