一种抽样二阶随机算法

王静 王湘美

(贵州大学数学与统计学院,贵阳,550025)

1 引言

考虑以下优化问题:

其中每个fi:Rd →R 是定义在欧氏空间上的连续可微函数.这类问题在数据拟合、回归分析、参数估计、无线传感网络中的分布式优化、神经网络训练、机器学习等方面有广泛的应用.梯度法和牛顿法等确定性算法是求解优化问题的经典算法.然而当问题(1.1)的规模很大(n很大)时,确定性算法每次迭代要计算所有fi的梯度(牛顿法还要计算所有fi的Hessian 矩阵),这导致每步迭代的计算成本和存储成本都很高.因此,一些学者提出并研究了求解大规模问题(1.1)的一阶随机算法和二阶随机算法.一阶随机算法(也称为随机梯度算法)是结合梯度算法和随机算法的思想提出来的.自从1951 年Robbins 等[1]提出采用常值步长的随机梯度算法SGD 后,一阶随机算法已经成为训练学习模型的重要算法.SGD 算法为了保证收敛,其迭代步长随着迭代次数的增加需趋于零,这通常会导致算法迭代到一定次数后收敛速度变慢.后来,Roux 等[2]提出了随机平均梯度算法SAG,该算法为每个样本保留一个旧梯度,在每次更新时随机选取一个样本计算新梯度来替换掉该样本的旧梯度,然后用所有样本梯度的平均值作为下一步更新的负方向.Roux 等证明了在一定条件下SAG 算法线性收敛.但是SAG 算法需要为每个样本设置一个内存空间，这就导致内存很大.为了解决这个问题,Johnson 等[3]提出了随机方差减小梯度算法SVRG.SVRG 算法相对于SAG 算法而言,不需要在内存中为每个样本都保留一个梯度,节省了内存资源.当使用小批样本梯度的均值估计全部样本梯度的均值时会产生方差.Johnson 等指出SAG 算法和SVRG 算法之所以线性收敛,是因为两种算法都减小了方差的干扰.之后，在减小方差这一思想的影响下,学者们提出了许多一阶随机梯度算法,见文献[4-7].另外,应用在Pytorch 和Tensorflow 中的随机一阶算法见文献[8-14].

与一阶随机算法相比,二阶随机算法除了用到一阶导数信息还要用到二阶导数信息.牛顿法是经典的二阶优化算法,它在一定条件下具有二阶收敛速度,其迭代公式如下:

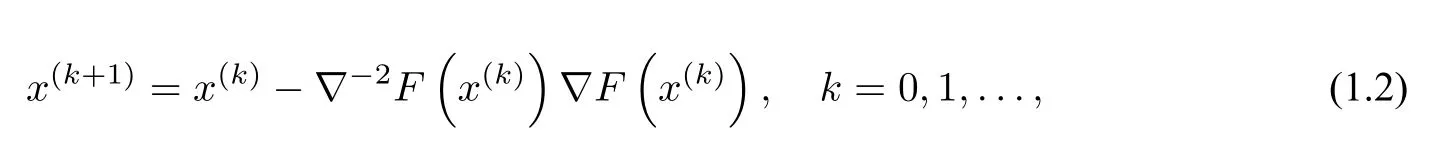
本文将Lissa 算法和SSN 算法结合起来，给出一种SSN-Lissa 算法.该算法首先采用SSN 算法的抽样方法计算随机梯度,然后采用Lissa 算法基于泰勒公式A-1=(I -A)i估计Hessian矩阵的逆,并采用类似于SSN 算法的步长规则计算步长.此外,我们还对SSN-Lissa 算法的全局线性收敛性进行证明,并通过数值实验说明SSN-Lissa 算法比Lissa 算法和SSN 算法精度更高,每步迭代的时间成本更低.

本文余下部分安排如下:第二节介绍预备知识;第三节给出SSN-Lissa 算法及其收敛性证明;第四节通过数值实验验证SSN-Lissa 算法的有效性.

2 预备知识

设v ∈Rd,V ∈Rd×d.我们用‖v‖和‖V‖分别表示向量v的2-范数和矩阵V的谱范数.对于两个实对称矩阵A和B,用A ≥B表示A-B是半正定矩阵.对于二阶连续可微函数f:Rd →R,我们用∇f(x)和∇2f(x)分别表示f在点x处的梯度和Hessian 矩阵;若Hessian 矩阵∇2f(x)可逆,则用∇-2f(x)表示它的逆矩阵.

下面的引理是常见的，容易用定义证明，其中I表示d阶单位矩阵.

引理1设A ∈Rd×d.如果‖A‖≤1 且A正定,则有

我们对问题(1.1)中的函数做以下假设.

假设H1fi二阶连续可微,且存在0＜mi ≤Mi ≤1,使得

显然,在此假设下,存在0＜γ ≤K ≤1,使得

注1在本文的算法收敛性分析中,需要假设H1成立.幸运的是,对于很多机器学习问题的模型,例如岭回归模型、逻辑回归模型等,假设H1都是成立的,详见附录表3 或参考文献[9,15,17,18,19,24].

(2.4)表明函数F强凸且∇2F的特征值介于γ和K之间.此时优化问题(1.1)的解x*存在、唯一，且满足

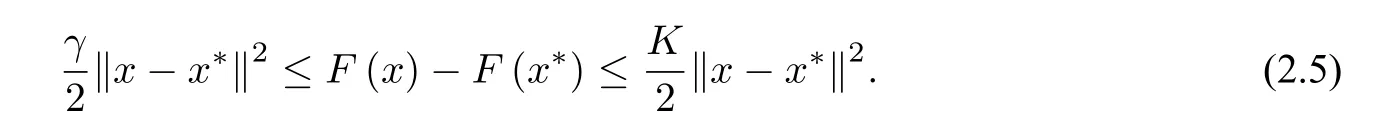
我们称κ=为问题(1.1)的条件数.

设X ∈Rd×d是d阶随机矩阵.用E[X]表示X的数学期望.由(2.2),(2.3)和(2.4)式,可以得到如下引理(见文献[18]).

引理2设优化问题(1.1)中函数F满足(2.3)和(2.4),{h1,h2,···,hT}是总体的一组样本,其中T为样本数.令

设A是一个随机事件,用Pr(A)表示事件A发生的概率.以下引理是关于随机矩阵范数的概率估计(见[23,Theorem 1.3]).

引理3设Y是d阶随机实对称矩阵,且满足E(Y)=0,Pr(‖Y‖≤R)=1.则对于任意t ≥0有

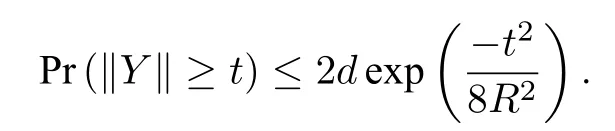
引理4设由(2.6)定义,ε1∈(0,1).如果样本数T满足

由(2.4)知∇2F(x)正定且‖∇2F(x)‖≤1.再由引理1 可得

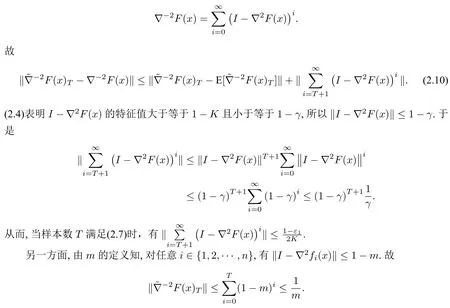
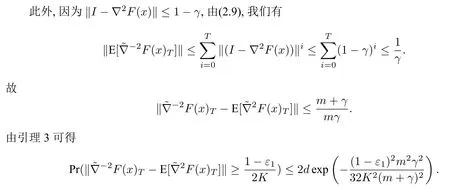
结合(2.10)可知(2.8)成立.

下面的估计式将在算法收敛性分析中起到重要作用.

命题1设由(2.6)定义,ε1∈(0,1).如果样本数T满足(2.7),则

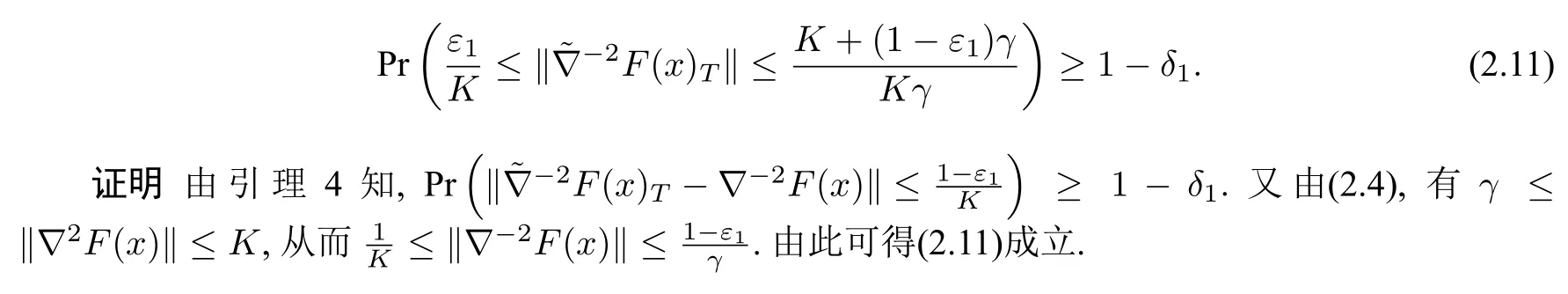
设非空集合S ⊆{1,2,···,n},用符号|S|表示集合S中元素的个数.定义函数g:Rd →R 如下:

我们称g(x)为∇F(x)的一个随机抽样.

下面的引理给出在概率意义下g和∇F的近似程度(见[19,Lemma 2]).为此我们需要以下假设.

假设H2存在函数G:Rd →R 使得对任意的i=1,2,···,n，有

引理5设H2成立.若对任意的ε2,δ2∈(0,1),|S|满足

则有

注2在假设H2中，需要事先确定G(x).幸运的是,在很多机器学习问题中，G(x)常常可以事先给出,详见附录表4.

3 SSN-Lissa 算法及收敛性分析

为求解问题(1.1),我们给出以下二阶随机算法(SSN-Lissa 算法).

注3SSN-Lissa 算法是将Lissa 算法([18,Algorithm 1])和SSN 算法([19,Algorithm 4])结合起来的一种二阶算法，与Lissa 算法异同之处主要体现在以下两个方面:一是两种算法采用相同的Hessian 矩阵逆的近似计算方法,但是Lissa 算法采用函数的全梯度,而SSN-Lissa 算法采用随机梯度;二是步长的选取不一样,Lissa 算法步长为1,而SSN-Lissa 算法采用步长(3.2).SSN-Lissa与SSN 算法的异同则主要体现在两种算法采用相同方式产生随机梯度,但是对Hessian 矩阵或者Hessian 矩阵逆的估计不一样.

注4SSN-Lissa 算法一次迭代可以分为两步.第一步用公式(2.12)计算当前迭代点的随机梯度,其中抽取的函数个数|S|满足(2.13).这里需要设置参数δ2∈(0,1)与ε2.δ2,ε2越小,随机梯度越接近真实梯度∇F(x(k));第二步是估计当前迭代点的Hessian 矩阵的逆,抽取的Hessian 矩阵的样本数,即Taylor 展开的深度T越大，越接近真实Hessian矩阵的逆∇-2F(x(k)).

我们分别按以下方式选取参数ε2和步长αk（k=1,2,···）:

其中ε,ε1,β ∈(0,1)为任意给定的常数.此时,SSN-Lissa 算法有如下收敛性结果.

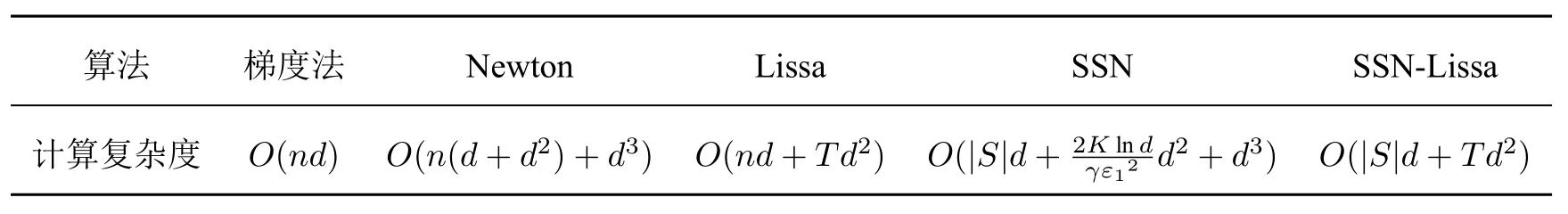
表1 确定性算法、随机算法一次迭代的计算复杂度对比

注6从表1 看出,当|S|和T远小于问题的规模n时,随机算法(Lissa,SSN,SSN-Lissa)的计算成本远小于确定性算法(例如梯度法,Newton 法).在下一节的数值实验中,n=9847.在三次迭代之后，|S|≤120,T=5,SSN-Lissa 算法的|S|和T都远小于n,同时也比SSN 算法和Lissa 算法计算成本低.当训练样本数n和优化参数d都很大时,SSN-Lissa 算法更加具有优势,这一点在后面的数值实验中也有体现.

4 数值实验

实验采用MNIST-49 数据集进行二分类学习,数据集包含9847 张训练样本图片,1991 张测试样本图片.我们采用附录中逻辑斯蒂回归模型进行训练.在训练中,设置参数λ=0.5,β=0.4,δ2=0.7,ε1分别设置为0.9,0.7,0.5,0.3,0.1,其他参数我们按照下表设置.

表2 实验参数的设置

由定理1 我们知道SSN-Lissa 算法是概率意义下的下降算法,故我们在运行算法时采用如下更新方式:当F(x(k+1))＜F(x(k))时我们更新迭代点,当时则不更新迭代点.算法随机产生初始迭代点,通过SSN-Lissa 算法对数据进行20 次训练,比较当选择不同ε1时SSN-Lissa 算法的性能(图1).

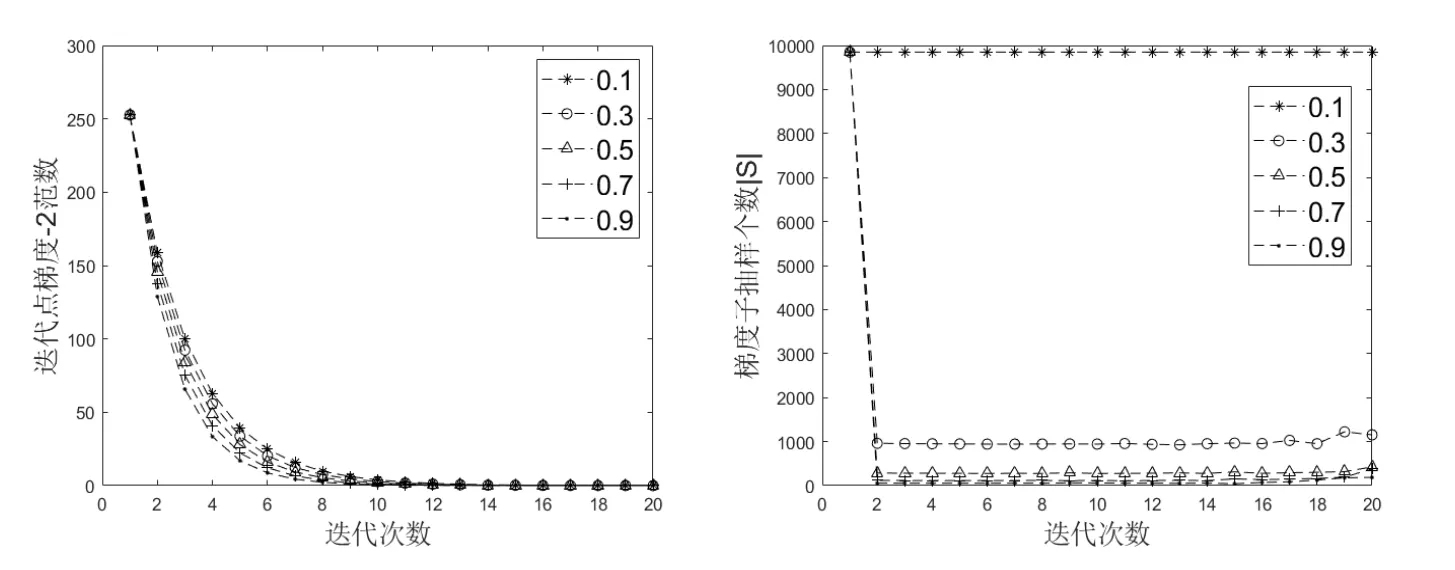
图1 选择不同ε1,对改进SSN-Lissa 算法性能进行比较

从图1 可以看出,SSN-Lissa 算法是下降算法.由于算法的初始点是随机产生的,故SSN-Lissa算法是全局收敛.同时,我们观察到,当参数ε1变大时,算法的收敛速度变快.这一现象不难理解,定理1 说明算法的收敛速度取决于的值，且ε1越大,收敛速度越快.当设置ε1＞0.5时,|S|≤120,仍然线性收敛.不仅如此,随着ε1的增大,|S|的期望在减小.值得注意的是,随着ε1的增大,|S|在减小(意味着每一步迭代所消耗的时间成本降低).我们观察到|S|在第2 步之后变化不大，故我们仅计算前几步|S|，以后的|S|用前几步|S|的平均值替代,进一步降低了每一步迭代所消耗的时间成本.

图2 是关于SSN-Lissa 算法、Lissa 算法、SSN 算法在运行时间和函数值的比较.迭代20 次，其中SSN-Lissa 算法设置ε1=0.9，|S|采取两种方案:一种方案是每一步更新|S|;另一种方案是仅更新前两步|S|,第三步以后的|S|用前两步|S|的平均值替代.Lissa 算法和SSN 算法分别按照文献[18]和[19]提供的数值实验设置参数.

对比图2 中的三种算法,SSN-lissa 算法每步迭代的时间成本最低.这是因为SSN-Lissa 算法随机计算部分函数梯度而Lissa 需要计算所有函数梯度,并且SSN-Lissa 算法直接估计Hessian 矩阵的逆,比SSN 算法(先估计Hessian 矩阵然后在计算逆)时间成本低.通过对比不同初始点的选取对三种算法的影响,发现当初始点离最优点较远时(中间图)SSN-Lissa 的函数值下降最快,其次是SSN.这是因为SSN-Lissa 算法和SSN 算法都可以达到全局线性收敛,而Lissa 算法仅在初始点接近最优点时达到线性收敛.当初始点在最优点附近时(右边图)Lissa 算法函数值在第一步有很快的下降,之后趋于平稳,而SSN-Lissa 算法虽然刚开始没有Lissa 算法下降快,但是迭代6 次之后就达到了Lissa 算法的精度.

我们接下来的工作有两个方面,第一方面是在SSN-Lissa 算法中考虑方差减小的思想;另一方面是用其他方式近似求Hessian 矩阵的逆.

图2 SSN-Lissa(ε1=0.9),SSN,Lissa 三种算法性能对比

附录A

考虑带正则化的高斯先验的最大后验问题(详见[19]),其目标函数为:

其中0＜λ ≤0.5 为正则化参数,表示n组训练数据,其中ai ∈Rd,bi ∈R.根据bi的不同取值,对应采用不同的模型Φ(t).例如当bi ∈R,Φ(t):=0.5t2时,采用的模型为岭回归模型(RR);当bi ∈{0,1},Φ(t)=ln(1+exp(t)) 时,采用的模型为逻辑回归模型(LR); 当bi ∈{0,1,2,···},Φ(t)=exp(t)时,采用的模型为泊松回归模型(PR).有关更多细节和应用程序,请参阅[24].值得注意的是,为了使数据比较集中,可以对全部ai进行等倍缩放处理,使得‖ai‖2≤0.5,bi的值保持不变.为了减少符号的滥用,在不影响理解的情况下,预处理后的数据依然记为.容易验证F的梯度和Hessian 矩阵分别为

在SSN-Lissa 算法的收敛性证明中需要问题(1.1)中函数满足条件假设H1,表A1 说明岭回归模型、逻辑回归模型满足假设H1.

表A1 假设H1 中mi 和Mi

引理5 中的|S|依赖于G(x(k)),表A2 给出了G(x)的一些估计.从表A2 可以看到,每次估计G(x(k))只需要计算‖x(k)‖.

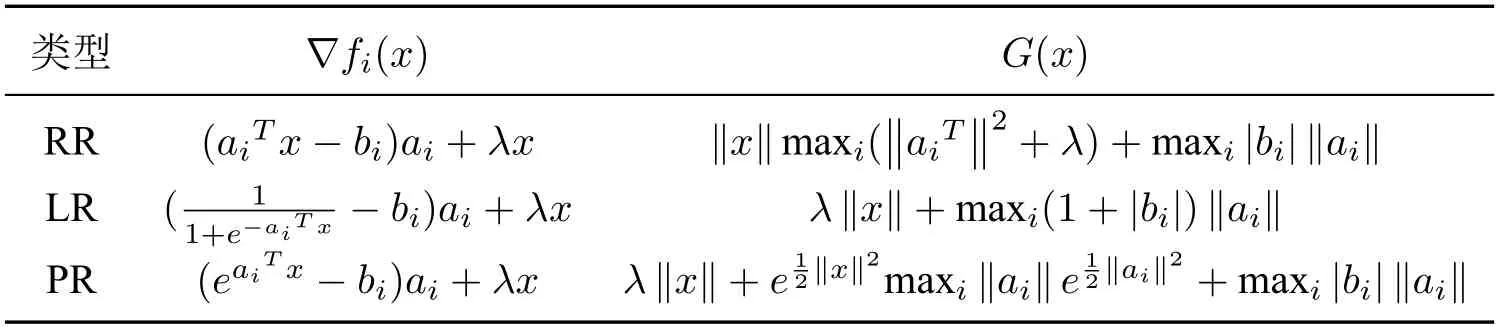
表A2 假设H2 中G(x)的估计