The Greatest Common Divisor of Certain Set of Binomial Coefficients
2022-04-15XiaoJiaqiYuanPingzhiLinXucan
Xiao Jiaqi Yuan Pingzhi Lin Xucan
(School of Mathematical Science,South China Normal University,Guangzhou 510631,China)
Abstract In this paper,we prove that if n ≥4 and a ≥0 are integers satisfying,thenwhere,and the product in the right hand side runs through all primes p such that n=pm+b(n,p),m ∈N and 0 ≤b(n,p)≤a.As an application of our result,we give an answer to a problem in Hong[3].
Key words Binomial coefficient Greatest common divisor
1 Introduction


and proposed the following interesting problem:
Problem 1.1Letn ≥2 be an integer andb(n)be defined as above.Find the explicit formula for
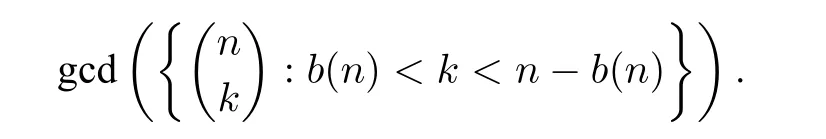
In 1859,Kummer[6]got the following result.
Theorem 1.1For any integers 0≤k ≤nand any primep:
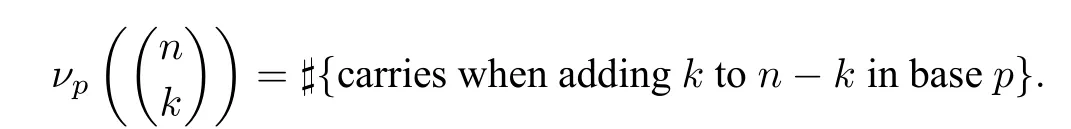
For any primep,we denote the sum of the standard base-pdigits ofnbyσp(n),i.e.σp(n):=ifn=withr ≥0 andaibeing integers such thatar >0 and 0≤ai ≤p-1 for all integersiwith 0≤i ≤r.
The main purpose of this paper is to give an answer to the above mentioned problem of Hong.We give an explicit formula for the greatest common divisor of the set of the binomial coefficients,wherekruns over all the integers betweenaandn-a.Letn ≥4 be a positive integer.For any primep ≤n,letpm,m ∈N be the largest prime power ofpwhich is less than or equal ton,and letb(n,p)=n-pm,thenn=pm+b(n,p),m ∈N.The main result of this paper is as follows.
Theorem 1.2Letn ≥4 anda ≥0 be integers with.Then
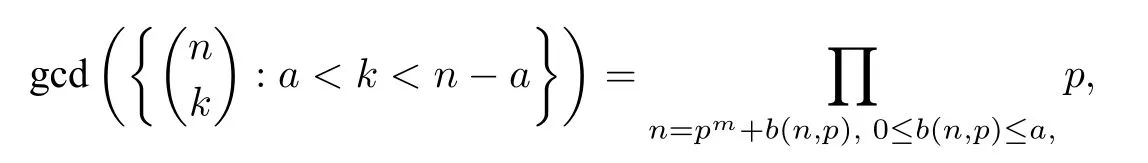
where the product runs through all primespsuch thatn=pm+b(n,p),m ∈N and 0≤b(n,p)≤a.
By the result of[11],we know thatb(n)≤,n=pm+b(n)for some positive integerm.Moreover,pis the only prime withn=pm+b(n,p),m ∈N and 0≤b(n)≤b(n,p).Therefore,as an immediate consequence of Theorem 1.2,we have the following result,which gives an answer to the above problem of Hong.
Corollary 1.1For any integern >0,letb(n)≥0 be the smallest integerbsuch that the binomial coefficients,whereb <k <n-b,has a(non-trivial)common divisor.Thenn=pm+b(n)for some primepand positive integerm,and
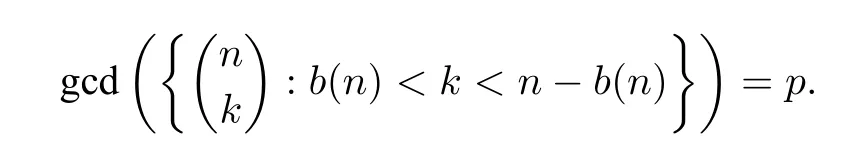
Remark 1.1It is easy to check that
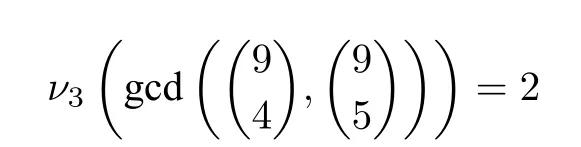
The arrangement of the paper is follows:In the Section 2,we prove several preliminary lemmas.Then we use these lemmas to prove Theorem 1.2 in Section 3.
2 Preliminaries
In this section,we prove some lemmas that are needed in the proof of Theorem 1.2.The following Lemma is essential in the sequel.


Lemma 2.3Letn ≥2,abe positive integers witha <n/2 and letpbe a prime.Ifn=pm+b(n,p),m ∈N and 0≤b(n,p)≤a,thenσp(k)+σp(n-k)≥p+σp(b(n,p))for every positive integerkwitha <k <n-a.
ProofBy the assumptions,we have


3 Proof of Theorem 1.2
In this section,we prove Theorem 1.2.


where the product runs through all primespsuch thatn=pm+b(n,p),m ∈N and 0≤b(n,p)≤a.This completes the proof of Theorem 1.2.
