The Difference of Mostar Index and Irregularity of Unicyclic and Bicyclic Graphs with Small Diameter
2022-04-15WuTingzengZengXiaolin
Wu Tingzeng Zeng Xiaolin
(School of Mathematics and Statistics,Qinghai Minzu University,Xining 810007,China)
Abstract Let G be a connected graph.Gao et al.first introduced the invariant of G:ΔM(G)=Mo(G)-irr(G),and raised a problem:how to determine the extremal graphs among all connected graphs of order n with respect to ΔM(G),where Mo(G)and irr(G)stand for the Mostar index and irregularity of G,respectively.In this paper,we characterize the upper bounds of ΔM(G)over all unicyclic graphs and bicyclic graphs with diameter 3,and determine the extremal graphs.
Key words Mostar index Irregularity Unicyclic graph Bicyclic graph Diameter
1 Introduction
Given a simple loopless finite undirected graphG=(V,E)with vertex setV={v1,v2,...,vn}and edge setE={e1,e2,...,em}.Letu ∈V.The degree of a vertexuis denoted bydu.The length of a shortest path between verticesuandvofGis called the distance connectinguwithv,denoted byd(u,v).The maximum distance between any two vertices ofGis called the diameter ofG.
Letuandvbe two vertices ofG,nuandnvdenote the number of vertices ofGcloser to vertexuthan to vertexvand the number of vertices ofGcloser to vertexvthan to vertexu.The Mostar index of a connected graphGis defined as[1]

which is well elaborated[2-7].
A graphGis called irregular if not all its vertices have a same degree.The irregularity ofGis defined as

which is introduced by Bell [10].For more studies on the irregularity of graphs,see [8,9,11] among others.
The ΔM(G)of a connected graphGis defined as
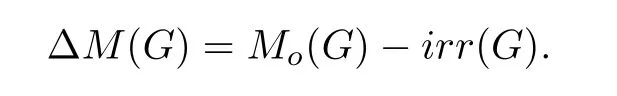
Gao et al.[12]first introduced the ΔM(G),and raised the following problem.
Problem 1.1How to determine the extremal graphs among all connected graphs of ordernwith respect to ΔM(G)?
In this paper,we determine the upper bounds of ΔM(G) over unicylic graphs and bicyclic graphs with diameter 3.The rest of this paper is organized as follows.In Section 2,we characterize the upper bound of ΔM(G)over all unicyclic graphs with diameter 3.In Section 3,we characterize the upper bound of ΔM(G)over all bicyclic graphs with diameter 3.In the final section,we summarize our results,and present a further problem.
2 The upper bound of ΔM(G)over unicyclic graphs with diameter 3
Feng et al.[13] determined all the unicyclic graphs withnvertices and diameter 3:S+(a,b),C3(a,b,c),C4(a,b)andC5(a,b),see Figure 1.In this section,we characterize the upper bound of ΔM(G)over all those unicyclic graphs.
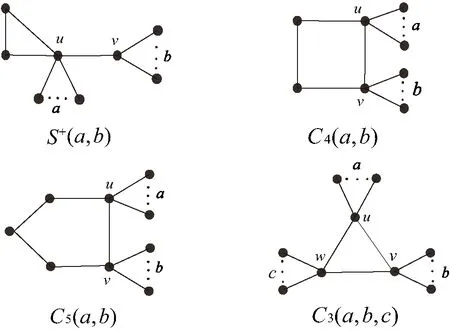
Figure 1 All unicyclic graphs with n vertices and diameter 3
Lemma 2.1LetG ∈S+(a,b).

ProofBy (1.1) and (1.2),we obtain thatMo(S+(a,b))=a(n -1) +b(n -3)+2n -4 andirr(S+(a,b))=a2+5a+b2-b+4.Thus,ΔM(G)=-a2+(n-6)a-b2+(n-2)b+2n-8.Now we use the method of Lagrange multipliers to find the upper bound of ΔM(G).Let
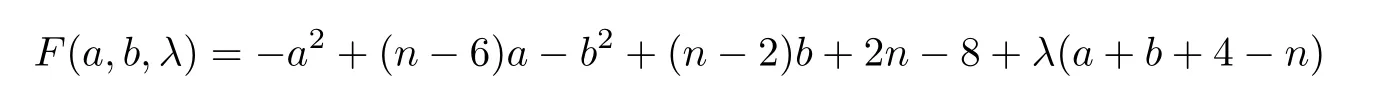
subject toa+b+4-n=0.Taking partial derivatives ofF(a,b,λ)with respect toa,bandλ,respectively,we obtain that

subject toa+b+4-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we obtain that



3 The upper bound of ΔM(G)over bicyclic graphs with diameter 3
In this section,we characterize the upper bound of ΔM(G)over all the bicyclic graphs withnvertices and diameter 3,which are showed in Figure 2.
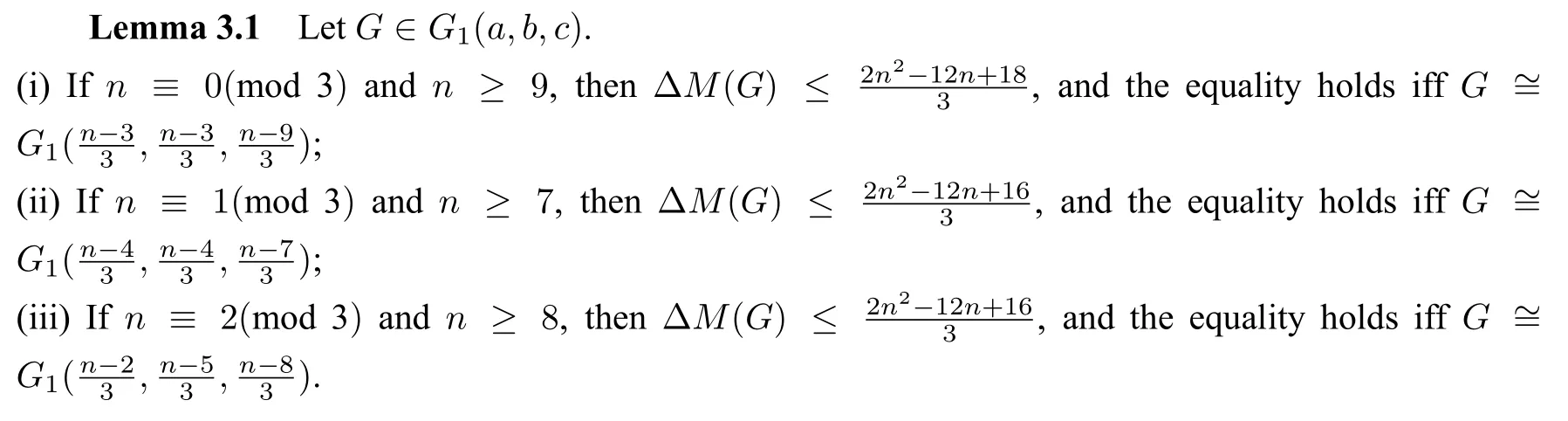
ProofBy(1.1)and(1.2),we can obtain thatMo(G1(a,b,c))=na+(n-2)b+(n-4)c+2n-10 andirr(G1(a,b,c))=a2+3a+b2+b+c2+3c.Thus,ΔM(G)=-a2+(n-3)a-b2+(n-3)bc2+(n-7)c+2n-10.Now we use the Lagrange multipliers to find the upper bound of ΔM(G).Let

subject toa+b+5-n=0.Taking the partial derivatives ofF(a,b,c,λ)with respect toa,b,candλ,respectively,we have
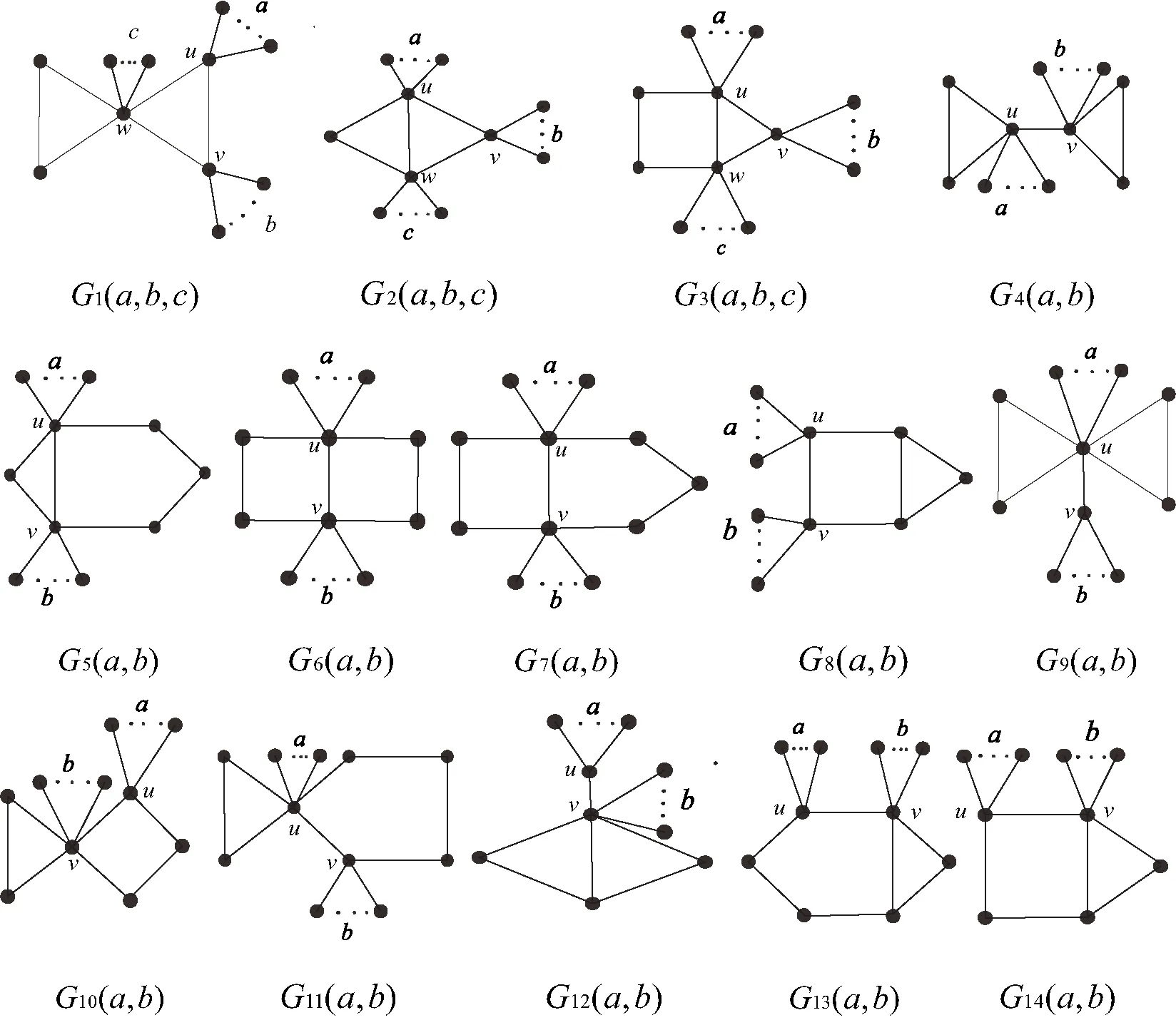
Figure 2 Bicyclic graphs with n vertices and diameter 3

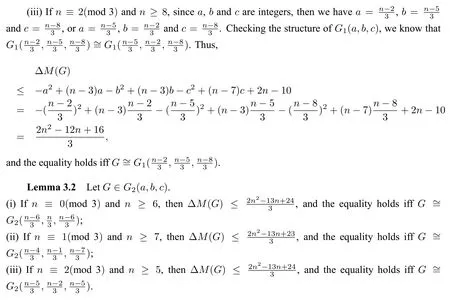
ProofBy(1.1)and(1.2),we can get thatMo(G2(a,b,c))=(n+1)a+nb+(n -3)c+2 andirr(G2(a,b,c))=a2+5a+b2+b+c2+c+2.Thus,ΔM(G)=-a2+(n-4)a-b2+(n-1)b-c2+(n-4)c.According to the method of Lagrange multipliers,we have
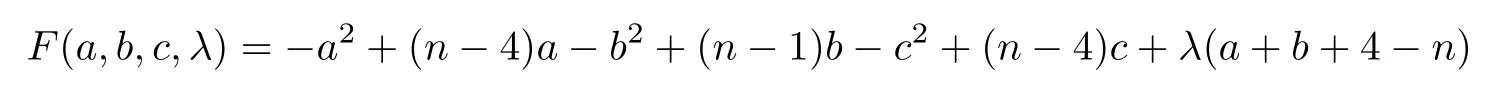
subject toa+b+4-n=0.Taking the partial derivatives ofF(a,b,c,λ)with respect toa,b,candλ,respectively,we get that


ProofBy (1.1) and (1.2),we haveMo(G3(a,b,c))=(n+3)a+nb+(n -3)c+2 andirr(G3(a,b,c))=a2+5a+b2+b+c2+c+2.Thus,ΔM(G)=-a2+(n-2)a-b2+(n-1)b-c2+(n-4)c.Now we use the method of Lagrange multipliers.Let

subject toa+b+5-n=0.Taking the partial derivatives ofF(a,b,c,λ)with respect toa,b,candλ,respectively,we have


ProofBy(1.1)and(1.2),we haveMo(G4(a,b))=(n-1)a+(n-3)b+4n-12 andirr(G4(a,b))=a2+5a+b2+3b+4.Thus,ΔM(G)=-a2+(n-6)a-b2+(n-6)b+4n-16.According to the method of Lagrange multipliers,we have

subject toa+b+6-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we get that

subject toa+b+6-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we obtain that

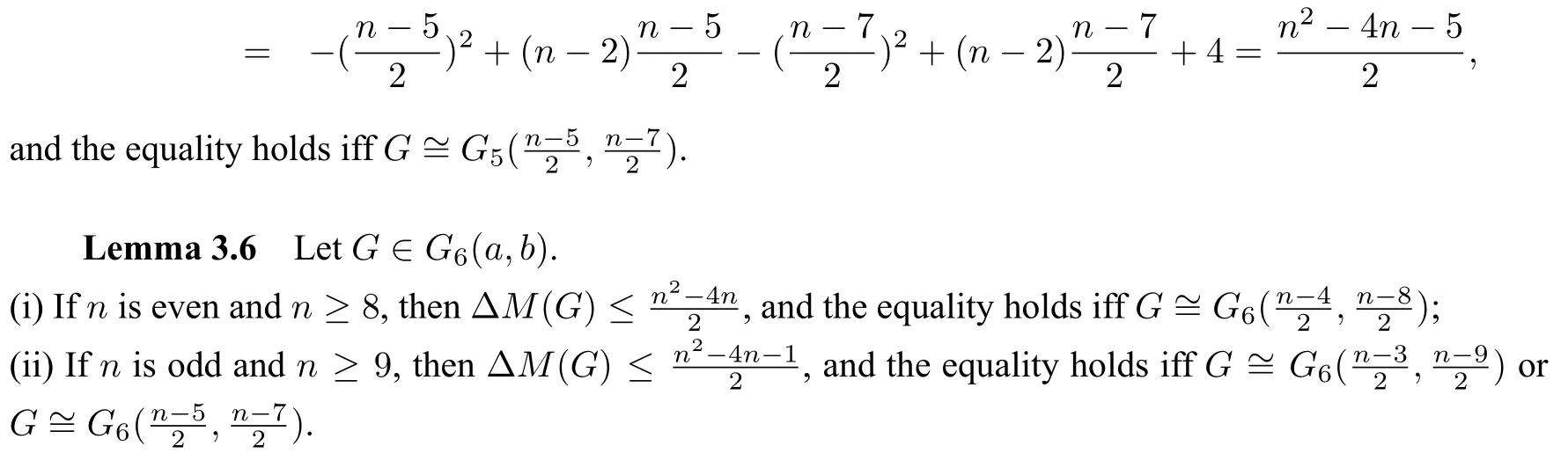
ProofSimilarly,by(1.1)and(1.2),we obtain thatMo(G6(a,b))=(n+5)a+(n-1)b+8 andirr(G6(a,b))=a2+5a+b2+3b+4.Thus,ΔM(G)=-a2+na-b2+(n-4)b+4.According to the method of Lagrange multipliers,we have
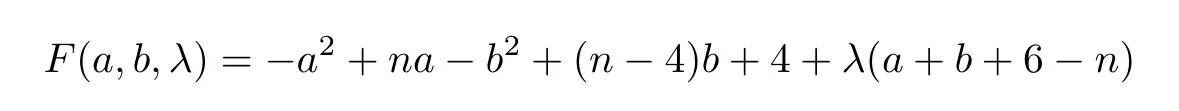
subject toa+b+6-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we get that

ProofBy(1.1)and(1.2),we haveMo(G7(a,b))=(n+5)a+(n+1)b+12 andirr(G7(a,b))=a2+5a+b2+3b+4.Thus,ΔM(G)=-a2+na-b2+(n-2)b+8.According to the method of Lagrange multipliers,we have
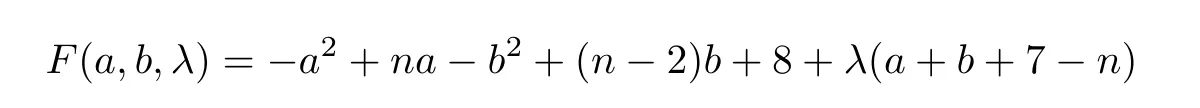
subject toa+b+7-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we obtain that

ProofBy (1.1) and (1.2),we haveMo(G8(a,b))=(n+3)a+(n -1)bandirr(G8(a,b))=a2+3a+b2+b.Thus,ΔM(G)=-a2+na-b2+(n-2)b.By the method of Lagrange multipliers,we have
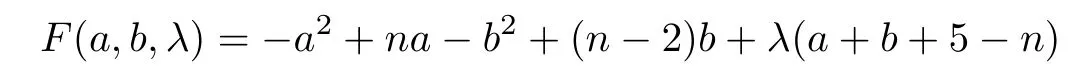
subject toa+b+5-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we have
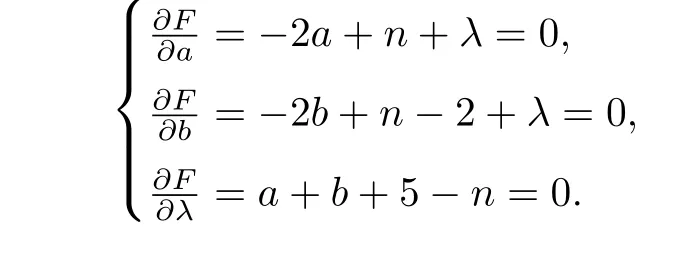

ProofBy (1.1) and (1.2),we can get thatMo(G9(a,b))=(n -1)a+(n -3)b+4n -8 andirr(G9(a,b))=a2+9a+b2-b+16.Thus,ΔM(G)=-a2+(n-10)a-b2+(n-2)b+4n-24.Now we use the method of Lagrange multipliers.Let
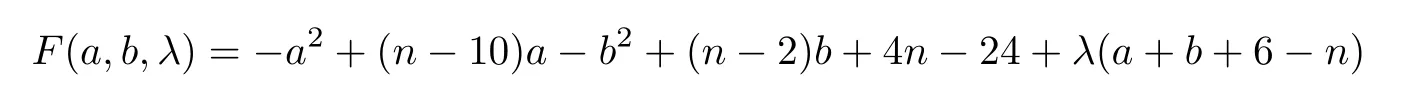
subject toa+b+6-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we get that
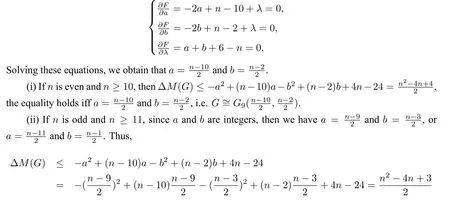
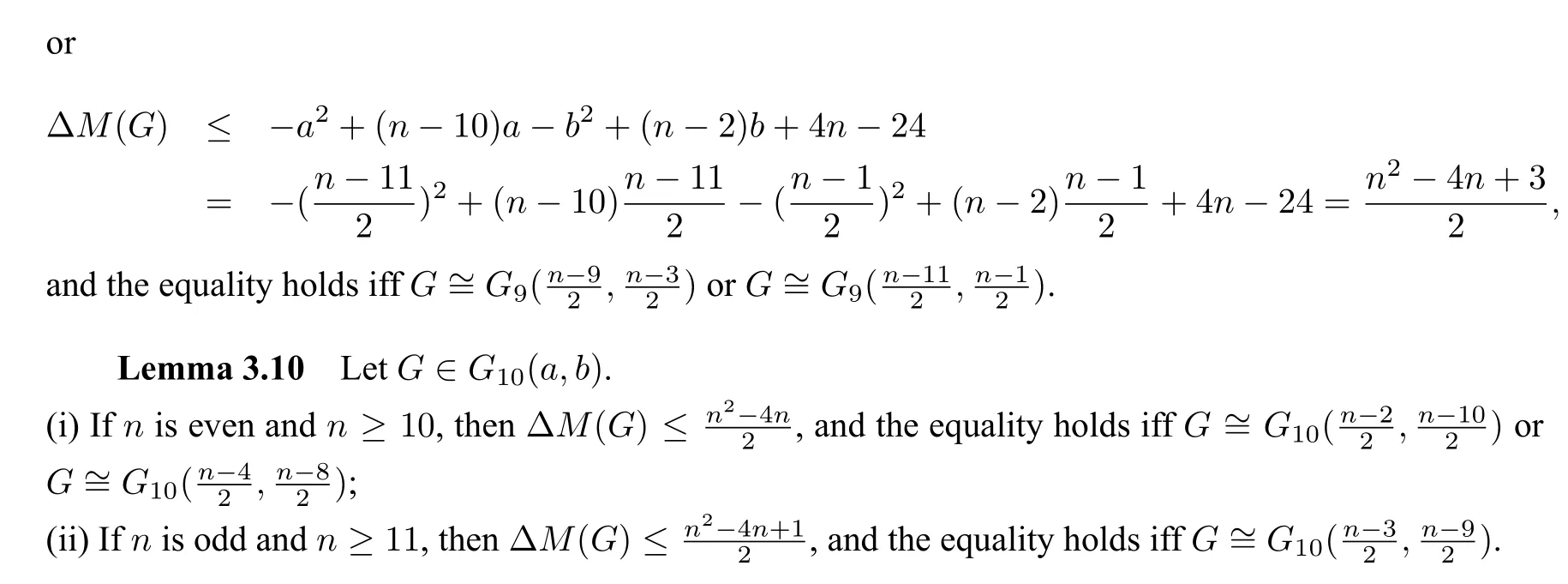
ProofBy(1.1)and(1.2),we can get thatMo(G10(a,b))=(n+4)a+nb+6 andirr(G10(a,b))=a2+3a+b2+5b+6.Thus,ΔM(G)=-a2+(n+1)a-b2+(n-5)b+2.We use the method of Lagrange multipliers.Let
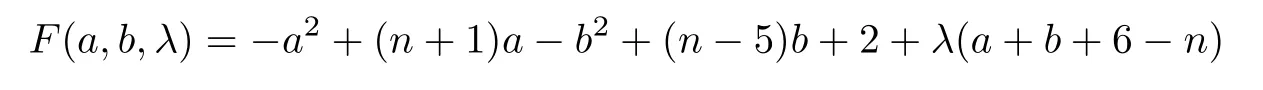
subject toa+b+6-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we obtain that

ProofSimilarly,by (1.1) and (1.2),we haveMo(G11(a,b))=(n+4)a+(n+2)b+16 andirr(G11(a,b))=a2+7a+b2+b+8.Thus,ΔM(G)=-a2+(n-3)a-b2+(n+1)b+8.By the method of Lagrange multipliers,we have

subject toa+b+7-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we have

ProofBy (1.1) and (1.2),we haveMo(G12(a,b))=(n+2)a+nb+4 andirr(G12(a,b))=a2+a+b2+5b+4.Thus,ΔM(G)=-a2+(n+1)a-b2+(n-5)b.Now we use the method of Lagrange multipliers to find the upper bound of ΔM(G).Let

subject toa+b+5-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we obtain that
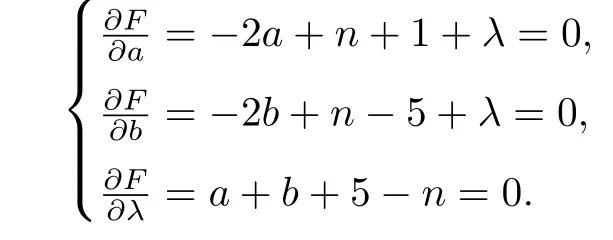

ProofBy(1.1)and(1.2),we haveMo(G13(a,b))=(n+3)a+(n+1)b+4 andirr(G13(a,b))=a2+3a+b2+3b+2.Thus,ΔM(G)=-a2+na-b2+(n-2)b+2.According to the method of Lagrange multipliers,we have

subject toa+b+6-n=0.Taking the partial derivatives ofF(a,b,λ) with respect toa,bandλ,respectively,we get that


ProofBy(1.1)and(1.2),we haveMo(G14(a,b))=(n+1)a+(n+1)b+2+2|a-(b+1)|andirr(G14(a,b))=a2+2a+b2+4b+3+|a-(b+1)|.Thus,ΔM(G)=-a2+na-b2+(n-4)b-2 or ΔM(G)=-a2+(n-2)a-b2+(n-2)b.Now we use the Lagrange multipliers to find the upper bound of ΔM(G).First,we discuss the maximum of ΔM(G)when ΔM(G)=-a2+na-b2+(n-4)b-2.Let
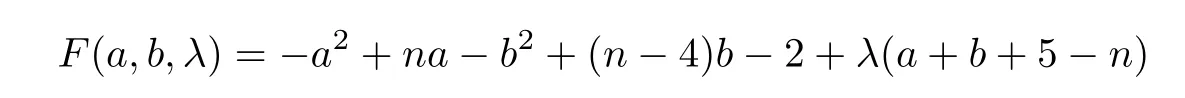
subject toa+b+5-n=0.Taking the partial derivatives ofa,bandλinF(a,b,λ),we have

subject toa+b+5-n=0.Taking the partial derivatives ofa,bandλinF(a,b,λ),we have

Combining the maximum values in Lemmas 3.1-3.14,we can get the following result.
Theorem 3.1be the set of all bicyclic graphs withnvertices and diameter 3.For anywe have
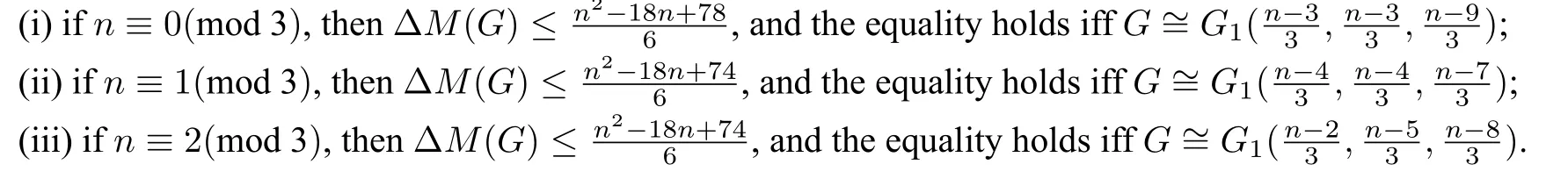
4 A futher problem
In this paper,we chararcterized the upper bounds of ΔM(G)for allG ∈Naturally,one may consider the following problem,which is probably much more difficult.
Problem 4.1Given aGhow can we determine the minimum value of ΔM(G)?
