基于自然邻居邻域图的无参数离群检测算法

冯骥，冉瑞生，魏延

（重庆师范大学 计算机与信息科学学院，重庆 401331）

随着大数据技术和数据密集型科学的发展，数据已经渗透到各个行业和业务功能中，成为了生产的一个重要因素。越来越多的国家、政府、行业、企业等机构已经意识到大数据正在成为组织最重要的资产，数据分析能力也已经成为组织的核心竞争力。目前，国家、政府已经把大数据应用推进了人们的生活中，大数据研究也成为了“十三五”期间的重点发展项目。

离群检测也是大数据战略中举足轻重的核心技术，在大数据技术发展日新月异之际，包括离群检测在内，数据挖掘中聚类、分类等技术也随之不断地进步与发展。离群检测的目的在于检测出数据集中那些被怀疑由异常机制产生的奇异数据，广泛应用于欺诈检测[1]、异常检测[2]、图像检测[3]、医学分析[4]、信号异常检测[5]等，并取得了众多令人满意的结果。

然而迄今为止，对离群的定义没有一个统一的认识，因离群定义的不同，离群检测算法的检测结果也会有所不同。本文将同时考虑全局离群点和局部离群点，提出了基于加权自然邻居邻域图的离群检测算法(weighted natural neighborhood graph outlier detection algorithm，WNaNG)。该算法利用加权自然邻居邻域图计算局部自然邻居离群度，找出离群度最高的n个离群点，而无需人为地预设邻域参数k。在此基础上，本算法可以利用离群度的离散图辅助挖掘出合理的离群点，或利用长尾理论直接根据离群度的分布找到合理的离群点区间，进而去除参数n，在无需邻域参数k的基础上将算法完善为完全无参数的离群检测算法。

1 传统离群检测算法

为了解决局部离群点的问题，基于密度的离群检测算法被陆续提出(例如LOF算法)。与距离度量不同的是，基于密度的离群检测算法通过定义各种不同的局部离群度来检测局部离群点。局部离群度往往能够准确地反映出数据点与其周围点密度特性上的差异，进而可以通过局部离群度的大小直观地找到离群点。这种方法在面对局部离群点时，往往能够取得更好的检测效果。

近年来，随着数据挖掘研究领域的不断深入，针对不同的应用领域，研究人员提出了大量的改进算法。Kim等[6]利用k-d树和近似k-最近邻居方法提出了一种高效的离群检测算法；Campello等[7]则提出了一种基于层次密度的数据挖掘算法，该算法提高了传统的基于密度的聚类效果，并通过计算得到层次化的聚类结果进行聚类、离群检测和数据可视化等多项任务。苟和平等[8]利用DBSCAN(density-based spatial clustering of applications with noise)算法对样本进行去噪和裁剪提出了KNN(k-nearest neighbor)算法的改进算法；周芳芳等[9]以体数据的标量值与梯度模直方图的密度分布为基础对传统算法进行了改进；周国兵等[10]基于算法空间复杂度的考虑提出了Bit kmeans算法；王习特等[11]提出了BOD(BDSP-based outlier detection)分布式离群点检测算法解决了传统的集中式算法处理效率受限的问题；陆海青等[12]提出的图像分割算法需根据图像噪声的强度适当地选取邻域窗口大小，并根据邻域窗口中各像素的灰度差异，利用指数函数进一步控制邻域像素的影响权重，实现像素灰度的自适应加权，从而提高像素灰度计算的准确性；赵冠哲等[13]提出的异常检测方法针对移动数据中历史位置和好友圈信息进行高效的检测，并在检测方法中探讨了针对不同情况时邻域参数的选择策略；张美琴等[14]提出了一种基于加权聚类集成的标签传播算法，该算法利用逆邻居的思想完成了计算基聚类集，进而利用基聚类集的加权相似性矩阵得到社区划分结果。

上述算法在各自的应用领域中均取得了令人满意的效果，进一步推动了相关技术的发展，却也同时凸显出了另一个亟待解决的问题——邻域参数对算法效率的影响。大多数基于距离和基于密度的离群检测算法的核心都架构于k-最近邻居思想，因此邻域参数的选择也就是k值的设置。k值较大会导致短路，使得算法在离群点检测中错误地将部分局部离群点归到正常点的范围中，而k值较小则会导致数据簇的不完整，将边缘点与稀疏点错误地归为局部离群点。更为困难的是，选择一个恰当具有非普适性的k值，在一个数据集中合适的k值通常在其他数据集中都会成为一个不恰当的选择。解决邻域参数的选取问题出现了两种思考的方向：探寻具有普适性的邻域参数选择方法，或降低邻域参数的敏感性。

Ha等[15]利用不稳定因子提出了一种新的对参数不敏感的离群检测算法INS(instability factor)。INS改善了KNN算法中离群检测算法对参数敏感的问题，使得离群检测的准确率能够在较大的范围内不会随着参数的改变而产生很大的变化，且可以检测出数据集中的全局和局部离群点。但是INS算法对参数的不敏感性牺牲了一部分离群检测的准确率，即INS的离群检测结果趋于稳定时检测准确率往往低于邻域参数选择合理时的其他算法。而且INS算法很难同时检测出局部离群点和全局离群点，检测局部离群点时需要调整不稳定因子的设定。

通过以上分析可以得知，现有的离群检测算法各自有各自的优势。但是，无论是基于距离的还是基于密度的算法都存在一个参数k值的设置问题，那就是如何选择一个合适的邻居个数k值。为了解决这一问题，本文选择结合自然邻居的思想提出适用于离群检测的普适性邻域参数选择方法。基于自然邻居形成过程无参的特性，本文提出了一种离群检测算法，该算法能够在已知离群点参数n的情况下无需邻域参数k找到数据集中的离群点。最后，算法探讨了完全无参数化的离群检测算法，在挖掘出正确的离群点的同时去除邻域参数k和离群点数量参数n。

2 基于自然邻居思想的离群检测算法

2.1 自然邻居概述

自然邻居思想是笔者及课题组成员提出的一种无尺度的概念，与传统的KNN方法相比，该思想能够在无需邻域参数k的情况下构建出合理的邻居关系，为后续的数据挖掘方法提供分析基础[16]。该思想包含以下几个核心概念。

定义1 搜索稳定状态(search stable state)

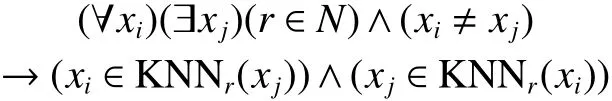
定义2 自然邻居(natural neighbor)

定义3 自然邻居特征值(natural neighbor eigenvalue)

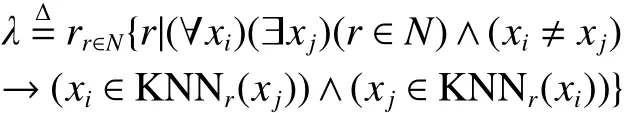
定义4 自然邻居邻域图(natural neighborhood graph)

在定义 1～4 中，数据集 X={x1, x2, ···, xn}，KNNr(xi)代表点xi的r邻域，即前r个邻居构成的集合，λ是自然邻居特征值，NN(xi)代表点xi的自然领域。自然邻居概念的定义在提出时就对该概念的扩展性进行了展望分析，而本文正是在此基本概念基础上，提出并构造加权自然邻居邻域图，并以此为基础完成无参数的离群点的检测算法。

2.2 基于加权自然邻居邻域图的离群检测算法

定义5 加权自然邻居邻域图(weighted natural neighborhood graph)。加权自然邻居邻域图反映了自然稳定状态时数据集中数据点之间的邻居关系，每一条加权边反映了对应的两个数据点首次互为邻居关系时的最近邻居搜索状态。加权自然邻居邻域图权值的形式化描述为

权值的取值范围为 [1，λ]。

定义6 自然邻居离群因子(natural neighbor outlier factor)。数据点p的自然邻居离群因子f (p)满足：

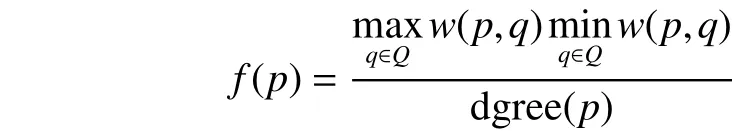
其中，集合Q ={q|e =(p,q)∈ E}，即Q为数据点p的所有自然邻居所构成的数据子集。

在完善了加权自然邻居邻域图和自然邻居离群因子的定义后，本文提出基于加权自然邻居邻域图的离群检测算法，算法流程如图1所示。

图1 基于加权自然邻居邻域图的离群检测算法流程图Fig. 1 Flowchart of the WNaNG outlier detection algorithm

算法1 基于加权自然邻居领域图的离群检测

输入 目标数据集X，离群点总数n；

输出 加权自然邻居邻域图G，局部离群点个数nl，全局离群点。

1) 初始化k=0，并创建数据集X对应的k-d树T；

2) 令k=k+1，并利用k-d树T找到数据集中每个点的k最近邻居；

3) 分析当前的邻居关系，将互为k最近邻居的两点构成一条边，并记录当前的k作为该边的权值；

4) 重复执行步骤2)～3)，直到数据集X中所有点都至少具有一个邻居，或连续r次未增加新的边，其中；

5) 将加权自然邻居邻域图中没有边的点标记为全局离群点，并计算出剩余的局部离群点个数nl；

6) 根据当前所有已知边的信息构造加权自然邻居邻域图。

自然邻居搜索算法通过自然邻居搜索过程和自然邻居邻域图的简单分析，找到了全局离群点，同时给出了剩余数据的加权自然邻居邻域图。算法得到的加权自然邻居邻域图将会被用于局部离群点挖掘过程，找到数据集中最终的局部离群点。

算法2 局部离群点挖掘算法

输入 加权自然邻居邻域图G=(V, E)，局部离群点个数nl；

输出 局部离群点。

1) 对邻域图进行遍历，找到每个点的所有加权边；

2) 根据定义6计算所有点的自然离群因子f；

3) 对所有点的自然离群因子进行降序排序，前nl个点即为局部离群点。

局部离群点挖掘算法首先计算加权自然邻居邻域图中点的自然邻居离群因子，其次依照离群因子的大小得到局部离群点。

2.3 自然邻居离群因子离散图分析

在上述算法的局部离群点挖掘算法中，剩余离群点依然需要人为设置，如算法中则是用离群点数量参数n减去已经找到的全局离群点个数。为了进一步完成无参数的离群点检测算法，本文尝试通过对自然邻居离群因子的离散图进行分析，去除离群点数量参数n，使得本文提出的离群检测算法具有更强的自适应性。因此，本文有针对性地构造了一个具有多个局部离群点的人工数据集，并针对其局部离群点的情况和自然邻居离群因子的值进行分析。

在图2中可以看到，数据点1、2、3、4和162、163、164、165为局部离群点。从图3中可以看出，图2中提到的离群点所对应的局部离群因子均远远高于普通数据点的局部离群因子，因此如果以自然邻居离群因子离散图作为辅助决策，可以直观地通过其数据分布确定自然邻居离群因子的阈值，并以此阈值作为局部离群点的判定标准，达到去除离群点数量参数n的目的。这种结合图形化展示的离群点检测方法使得离群点的度量和检测能够进行更为直观地展示。

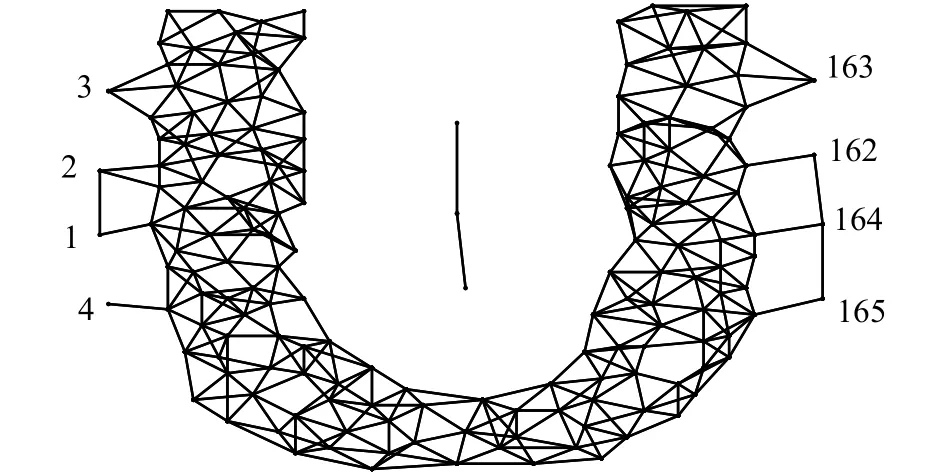
图2 自然邻居邻域图和局部离群点示意Fig. 2 Natural neighbor graph and local outliers

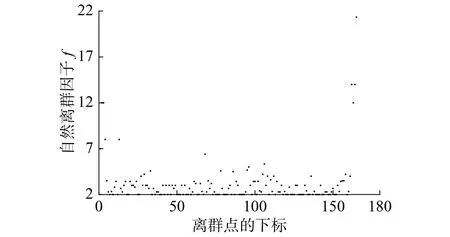
图3 数据集中各个数据点对应的自然邻居离群因子Fig. 3 Natural neighbor outlier factor of each data point

另外，若希望离群检测摆脱人为的参数设置和图像化辅助决策，在此选择对自然邻居离群因子进行降序排序，离群度的分布形态与长尾分布具有极高的相似度，因此可以尝试利用长尾分布的相关理论进行自然邻居离群因子的阈值确定，实现无需人为干涉、无需邻域参数k和离群点数量参数n的自适应离群检测算法。

2.4 算法复杂度分析

首先，自然邻居搜索算法在自然邻居查找和自然稳定状态的获取阶段时间复杂度为。其次，全局集群点和离群簇的挖掘均可以在邻居搜索的过程中完成，且并不会在数量级级别增加算法的时间复杂度。因此当前阶段的时间复杂度为。

在算法的第二阶段，局部离群点挖掘算法的时间复杂度要低于上一阶段。首先，自然邻居邻域图中的任意点最多具有λ条边，最少具有一条边。因此，自然邻居离群因子阶段的时间复杂度为，其中λ为一个较小的整数，因此该阶段实际复杂度为。之后的聚类分析具体操作时只需要对上一阶段中的数据簇结果进行简单的修改，而该修改操作的时间复杂度为。

3 实验结果

3.1 人工数据集实验

人工数据集的实验分为两部分。1)着重于展示本算法自适应性的优势，即与其他算法选择多个参数时能够获得的最好检测结果相比，本算法能够获得与之相似甚至于更好的结果，且无需选择邻域参数。在这一部分中，同一数据集中多个算法均选取相同的离群点数量n。2)分讨论算法在无需离群点数量参数n的情况下利用自然邻居离群因子查找局部离群点的算法结果。

首先进行基于邻域参数k的实验展示。本实验用到的人工数据集如图4所示。

图4中的6个数据集均包含了多个肉眼可见的离群点，其中既有局部离群点，又有全局离群点，且这6个数据集具有不同的数据分布特性，因而能更准确地反映出邻域参数对算法的影响，以及本算法的自适应性在面对数据集的多样性时的实际表现。

本文将基于加权自然邻居邻域图的数据挖掘算法与4种离群检测算法相对比，检验本算法与当前离群检测算法之间的性能差异，被选取的对比算法为KNN、LOF、INFLO和INS。

图5用曲线图展示了5种不同的离群检测算法在6个数据集中的检测精确率。为了更好地反映准确率随着邻域参数取值的变化而上下波动的详细情况，这里将x轴设定为邻域参数k的不同取值，y轴则是各个算法在选取每一个k值时对应的离群检测准确率。本算法克服了传统的邻域选择问题，即无需在算法中设置参数k，则在图5的所有子图中，WNaNG算法的准确率是确定的，即对固定的数据集，WNaNG算法只有一个确定的离群检测结果。为了算法对比效果的展示，WNaNG算法的准确率采用直线进行标示。

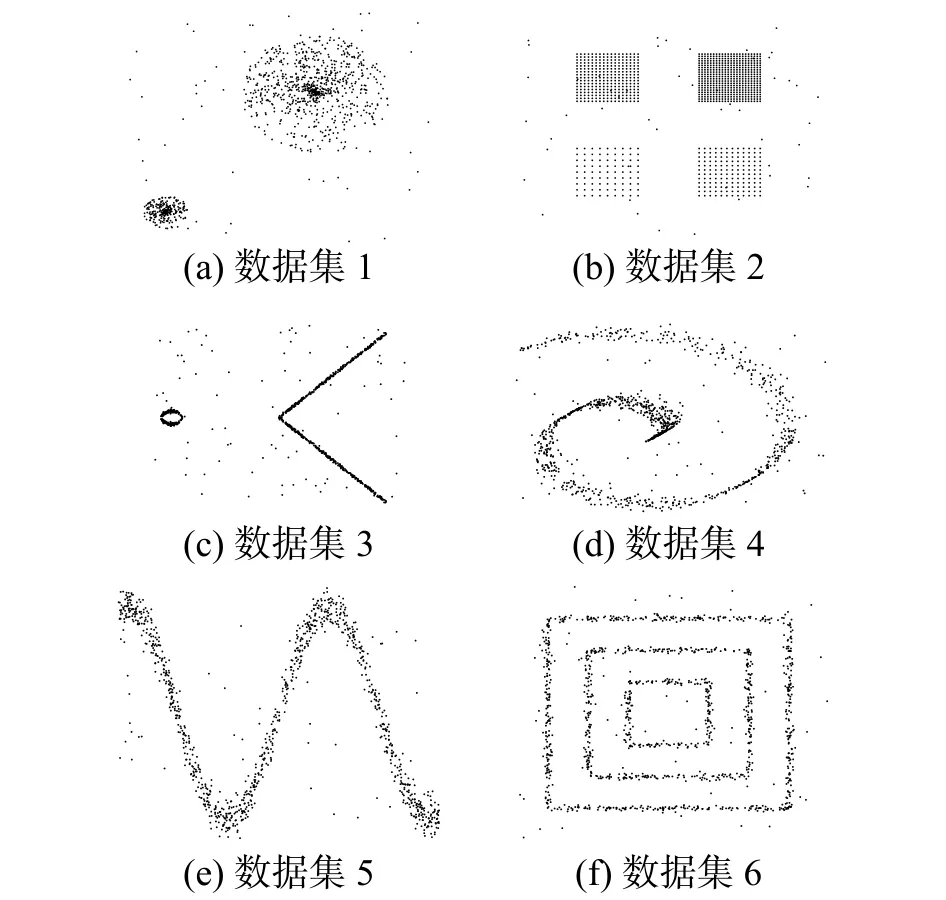
图4 包含离群点的6个人工数据集Fig. 4 Six synthetic data sets of the outliers

图5 5种离群检测算法在取不同k值时离群检测准确率对比Fig. 5 Outlier detection accuracies of five detection methods over a range of k values

纵观所有子图，WNaNG算法的普适性高于其余算法，能够在6个数据集中均取得令人满意的结果。若对每一个算法在各个数据集中均选择一个最优的参数k与本算法相比较，在数据集1中其余5种算法的最优算法略高于本算法，而在其余几个数据集中，其最优值基本仅能与本算法取得相似的检测效果，大部分的邻域参数值所对应的检测效果均与本算法有一定的差距。

从算法对邻域参数的适应性上看，本算法完全摆脱了邻域参数的影响，并取得了令人满意的结果；INS算法对邻域参数的敏感度较低，因此在各个数据集中，其检测结果不易随着邻域参数的变化产生剧烈波动；其余算法则对邻域参数较为敏感，特别是当数据集分布不规则时，如最后两个数据集中，邻域参数的选取会严重影响其算法结果。

产生上述情况的原因：为了降低邻域参数对算法的影响，增强算法的适应性，往往会在某些情况牺牲一部分离群检测准确率，如INS算法。而本文提出的WNaNG算法合理地利用了自适应的邻居特性，因而在保证了检测准确率的情况下移除了邻域参数的影响。本算法在与其余算法进行比较时检测结果呈现一条直线，并不是代表算法的检测结果不会随着k值的变化而产生变化，而是算法无需人为设置参数k。因此可以得到结论：WNaNG算法不仅解决了邻域参数的选取问题，更能在具有不同特性的数据集中取得稳定且准确的离群检测结果。本文将进一步讨论WN-aNG算法利用自然邻居离群因子查找局部离群点的实验结果。

图6展示了5个不同分布特点的数据集利用自然邻居离群因子进行局部离群点检测的检测结果。从实验结果中可以看到，在前两个数据集中，自然邻居离群因子的分布相对较为均匀，对应的数据集中局部离群点的特征也较弱；而在后几个数据集中，自然邻居离群因子的分布呈现较大的差异，能够通过分布图明显地划分出一个或者多个自然邻居离群因子突变界限，而这种情况也与实际数据分布相吻合，其数据集中的局部离群点在分布上也呈现出多层级的特点，即不同范围的离群点其局部离群特征也具有较大的差异性。

图6 局部离群点与自然邻居离群因子离散图Fig. 6 Local outliers and NaNOF scatter

3.2 真实数据集实验

真实数据集中本文采用的对比算法为KNN、LOF、INFLO和INS算法，算法对应的两个数据集分别为UCI 网站的CANCER和IRIS，采用的评价指标是离群检测的ROC曲线(receiver operating characteristic curve)，其横、纵坐标为离群点检测率和离群点数目，通过积分面积验证数据集在对应的k值选择中离群检测的效率。在两个人工数据集的实验结果中，基于加权自然邻居邻域图的数据挖掘算法由于不需要邻域参数，因此图中所展示的k为算法自适应得出的对应数据集的自然邻居特征值，其余算法则是其对应的邻域参数k的取值。

图7中的实验结果分为顶部和底部两组，顶部的实验结果为算法在对应的邻域参数k值的范围中选取得到的最差实验结果，而底部为该范围中最好的实验结果。从当前数据集可以看到，以离群点检测命中率作为检测结果时，INS和本算法的表现相对较差。这主要是由于，在CANCER数据集中，部分离群点被算法归为了簇，继而难以被检测出来，而其他3个算法能够更快地随着参数n的增加而找到那部分离群点。

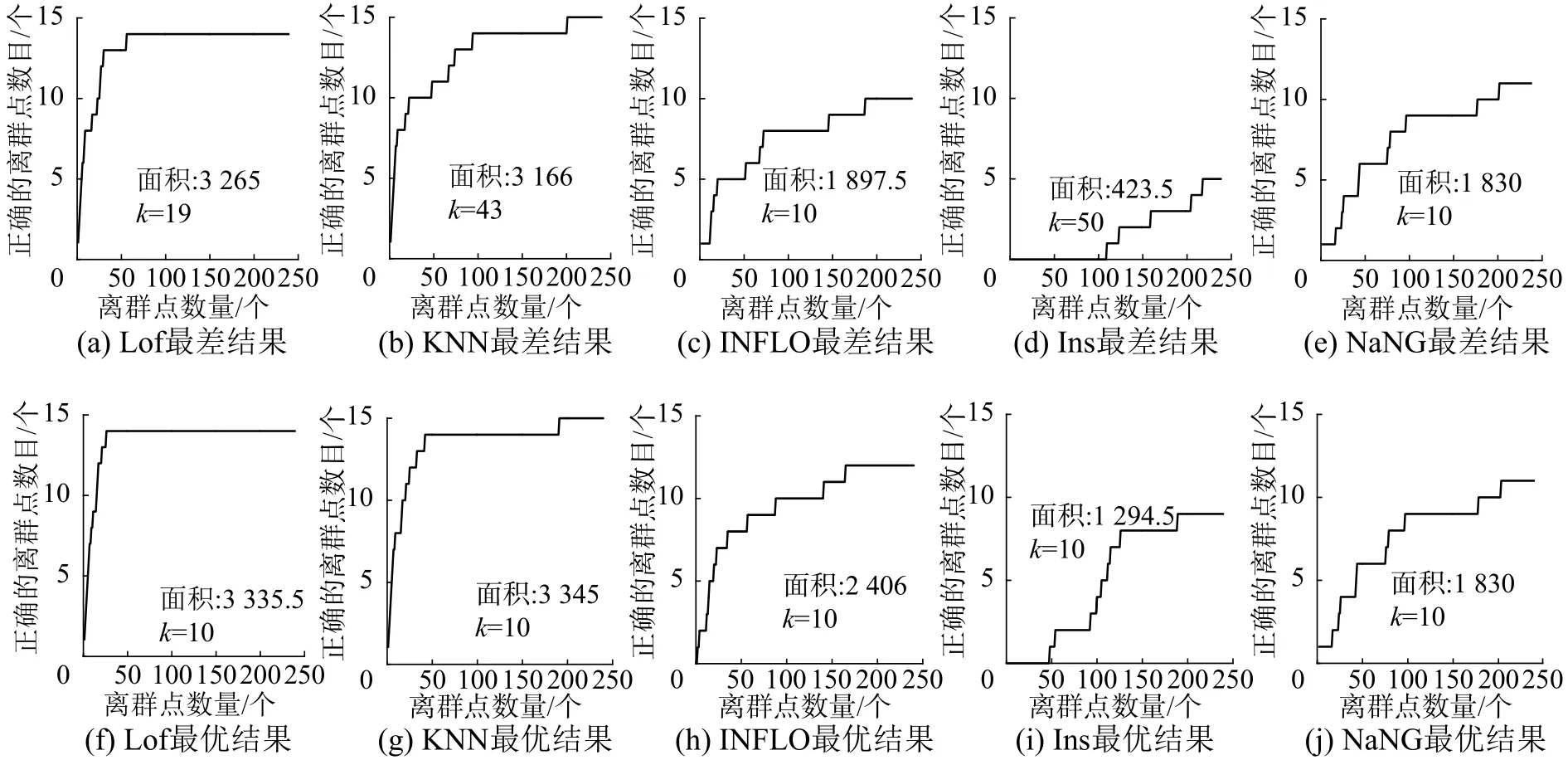
图7 CANCER数据集的ROC曲线下面积Fig. 7 Area under the ROC curves of CANCER

图8 的布局和图7相同，也是由最差实验结果和最佳实验结果组成。在IRIS数据集中，因为离群点中离群簇的情况比CANCER更少，因此WNaNG算法的结果有了明显的好转。特别是当n=50时，仅本算法就能够找到所有的离群点。

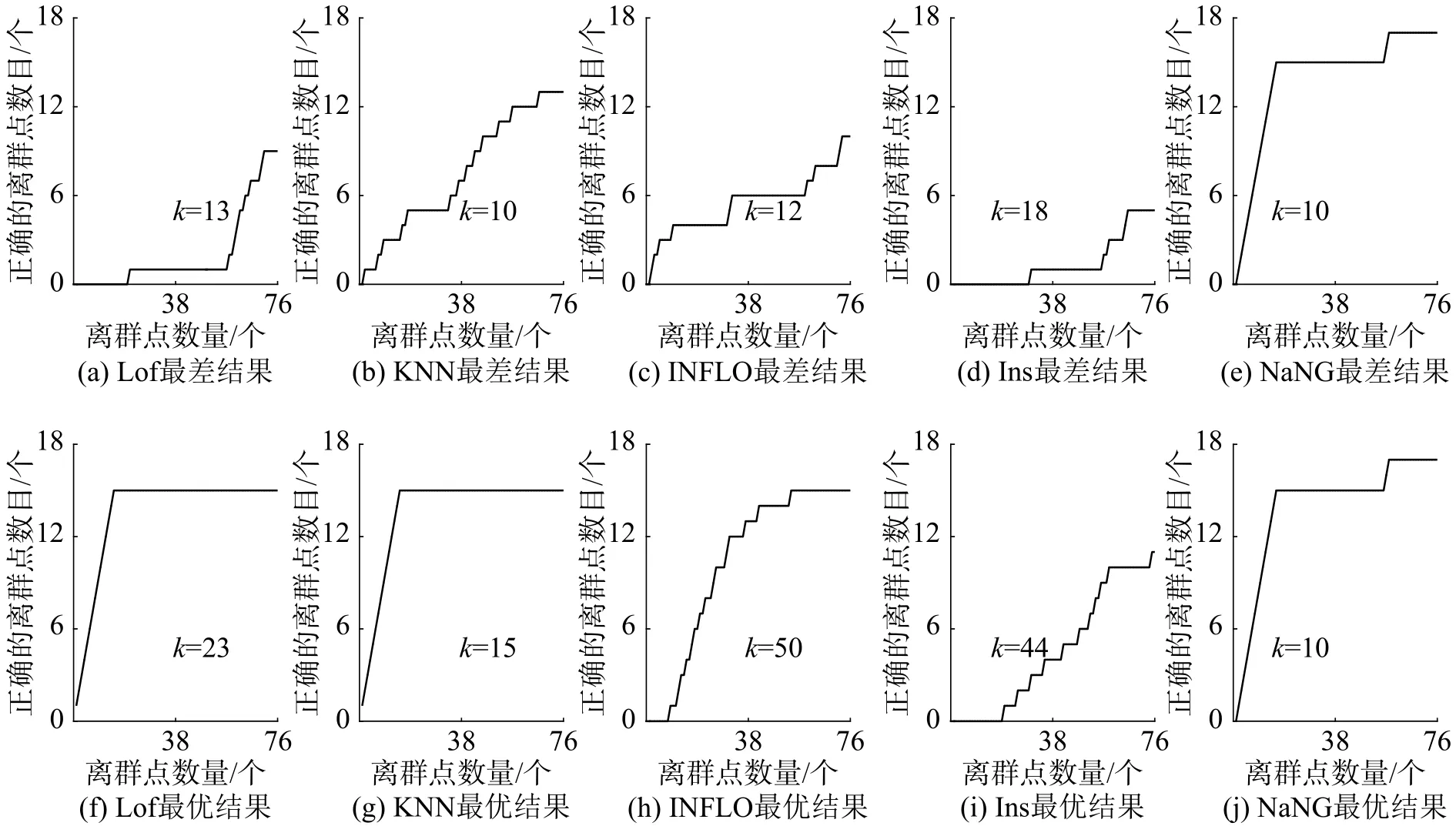
图8 IRIS数据集的ROC曲线下面积Fig. 8 Area under the ROC curves of IRIS

总结上述两个人工数据集的实验结果可以发现：WNaNG算法的离群检测结果不需要邻域参数，因此不存在邻域选择影响算法效率的问题；算法在两个数据集中均表现较为稳定，对不同的数据集均能获得较好的效果。INS算法需要邻域参数，虽然其对参数的容忍度较高，但从本实验中依然可以看到参数取值的最差情况和最好情况所对应的检测结果差距较大。其余3个算法在不同数据集、不同参数的情况下表现出了较大的波动，且针对不同数据集参数的最优取值之间没有规律，需要根据具体问题独立尝试。

4 结束语

针对离群检测中邻域参数、离群点总数参数以及局部离群点等问题，本文结合自然邻居思想提出了一种自适应的离群检测算法WN-aNG。该算法在不同的数据集中运行时无需人为设置邻域参数，并能够根据数据集自身的分布特征获得令人满意的检测结果。另外，WN-aNG能够更为准确地挖掘出局部离群点和全局离群点并予以区分，这也为离群点解释、释义空间的构建等数据挖掘的后续步骤提供了强有力的支持。