基于神经网络和遗传算法的铸锭晶体硅质量控制及工艺优化

郝佩瑶，朱金伟，廖继龙，郑丽丽，张 辉

(1.清华大学航天航空学院，北京 100084；2.江苏协鑫硅材料科技发展有限公司，徐州 221001；3.清华大学工程物理系，北京 100084)

0 引 言

效率、寿命和成本是太阳能电池研发中最重要的三个因素[1]。对应到硅片的生产中，需要以低成本生长出高质量的硅锭。影响铸锭晶体硅质量的热场控制核心参数包括晶体生长速度与生长界面温度梯度之比V/G、壁面热流q、生长界面高度差Δh和硅熔体内部温差ΔT等。以提高生产效率及晶体质量为目标研究晶体生长的热场特性，采用基于物理模型的数值方法模拟晶体生长过程成为有效的途径，一部分研究集中于通过二维或三维数值模拟优化热场[2-5]，如改变坩埚形状、加热器位置、隔热笼分隔块位置等。除了优化热场结构，另外一部分研究针对晶体生长过程的工艺控制参数进行优化[6-9]。然而使用传统的数值模拟方法及实验会耗费大量时间，如文献[8]中为了优化晶体生长工艺，需进行上千次稳态数值模拟。若对铸锭晶体硅生长过程进行一次瞬态数值模拟通常需要10 h左右[10]，实验则需要花费数天。另外数值模拟所采用的理论模型由于存在简化和假设，也导致模拟结果不能完全反映实际情况。人工神经网络作为机器学习的一种方法，可以通过对大量数据进行学习和归纳，充分挖掘样本数据中所蕴含的内在联系，实现快速准确预测，在一定程度上，训练完成的人工神经网络可以视为数值模拟的替代方法。

Asadian等[11]以Cz法生长YAG单晶为研究对象，通过二维稳态数值模拟的数据构建人工神经网络，以获得平直的晶体生长界面为目标，使用遗传算法对操作参数如提拉速率、晶体旋转速率、坩埚壁温度等进行优化。Dropka等[12]通过二维稳态CFD建模研究行进磁场形成的强制对流对于铸锭晶体硅生长界面形状的影响，将其用于人工神经网络训练的数据来源，寻找磁场参数和晶体生长参数之间的关系，并针对生长界面的平坦化使用高斯过程对磁场参数进行优化。Tsunooka等[13]针对SiC溶液生长过程对比了神经网络预测与CFD仿真模拟的计算速度，在该问题中预测速度比数值模拟快107倍。Dang等[10]使用二维瞬态模型对铸造准单晶硅的生长过程进行模拟，并将其作为人工神经网络训练的数据来源，以获得平直的晶体生长界面、降低晶体中的热应力和缩短晶体生长的时间作为优化目标，使用遗传算法对加热器降温速率和底部隔热笼的移动速率进行优化。Qi等[14]采用二维稳态整场模型模拟直拉单晶硅的生长过程，并将其用于训练人工神经网络，针对提高晶体生长界面平整度与降低界面氧浓度，结合遗传算法获得优化的晶体旋转速率和坩埚旋转速率。Dang等[15]将机器学习与遗传算法应用于SiC晶体的溶液生长过程优化。Yu等[16]采用机器学习与遗传算法相结合的方法对SiC晶体的溶液生长系统几何形状进行了优化。

以上研究主要通过人工神经网络等机器学习方法建立工艺参数与晶体生长过程参数之间的映射模型，大多以获得平直晶体生长界面为目标，采用优化算法对工艺参数进行优化。但是由于侧面加热，加之坩埚、熔体、晶体具有不同的热导率，使得实际晶体生长界面呈现曲面形状，而在坩埚侧壁则容易产生过冷区域，导致边缘异质形核形成随机取向多晶区，这些因素都会对晶体质量产生影响。针对铸锭晶体硅生长过程中的质量控制问题，采用人工神经网络与遗传算法相结合的方法研究晶体硅铸锭过程的重要参量V/G、壁面热流q、晶体生长界面高度差Δh、硅熔体温差ΔT对铸锭晶体硅的质量影响机理和规律，实现生长工艺的优化。首先采用人工神经网络方法建立工艺控制参数与以上参量的映射模型，并基于该模型研究工艺控制参数对晶体生长过程的影响规律，结合遗传算法对工艺控制参数进行优化以提高晶体质量，最后基于实际铸锭晶体硅生长过程的质量检测数据研究V/G对晶体生长过程及其质量的影响和控制策略。

1 物理和数学模型

建立人工神经网络模型首先需要确定的便是输入与输出变量，即选取哪些工艺参数和热场参数用于研究晶体生长过程。下面对所要研究的物理问题进行描述，说明所选择的4个热场参数对于晶体质量影响的重要性及必要性，确定输入与输出变量后以此为基础介绍人工神经网络与遗传算法的原理，最后说明建立人工神经网络模型所需的数据来源。

1.1 物理问题

图1为晶体硅铸锭炉示意图。加热器为顶侧五面加热结构，顶加热器附近和换热台顶部中心各有一热电偶，在晶体生长过程中通过底部隔热笼不断下移来增强辐射换热，使晶体生长持续进行，顶加热器采用定温控制，即通过热电偶1处的温度(TC1)来控制加热器功率，氩气从隔热笼顶部中心不断通入，用于冷却和带走杂质。在实际生产过程中，由于大多采用一个变压器控制侧加热器与顶加热器，侧、顶加热器的功率比在熔化、生长全过程中是固定的，难以适应晶体生长过程中热场的变化而得到高质量的晶体，因此如何动态调整功率比以实现高质量晶体生长，是需要研究解决的一个问题。

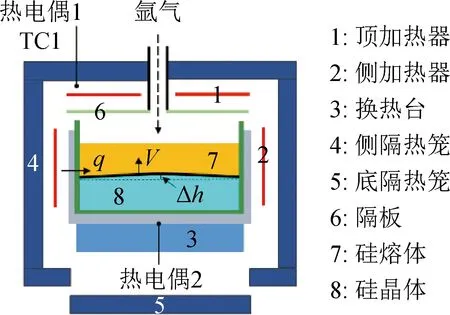
图1 晶体硅铸锭炉示意图Fig.1 Schematic diagram of silicon ingot furnace

在晶体硅铸锭过程中，平直或微凸的生长界面有利于保证晶粒垂直生长，减小水平方向的温度梯度，从而减小晶体内部的热应力，降低位错密度。另外由于分凝效应[17]，晶体硅生长的过程中杂质不断在生长界面处富集，微凸的生长界面能够促使杂质排向硅锭边缘，提高硅锭中间部分的品质。值得注意的是生长界面与坩埚壁接触处经常由于坩埚冷壁效应而成核，导致生长界面边缘出现下凹的形态，从而引起边缘多晶特别是孪晶侵入，降低硅锭的质量。为了提高硅锭品质，需尽量减小生长界面与壁面接触处的下凹程度，因此除了控制生长界面的高度差Δh以保证平直或微凸的界面，还需要对该处单位面积通过的热量q进行控制。

定向凝固技术的两个重要工艺参数是晶体生长速度V和生长界面处熔体中的温度梯度G，V/G是控制晶体长大形态的重要判据，在提高G的前提下增加V，才能获得较高质量的晶体[18]。由于晶体硅中存在的C、O等杂质以及B、P等掺杂剂的分凝系数k0一般小于1，使得在晶体生长的同时杂质不断被排到熔体中，在生长界面前沿形成溶质边界层，而熔体的凝固点随溶质浓度的增加而降低。如图2所示，在界面处熔体的凝固点由最初的Tm降为T0，在远离界面处凝固点仍为Tm。当熔体内温度梯度为正值但较小(温度分布②③)时，在温度曲线与凝固点变化曲线相交所形成的阴影区内，熔体的实际温度始终低于凝固点温度，使得这一部分熔体处于过冷状态。晶体生长过程中因干扰而在界面上产生的凸缘由于处在过冷度较大的熔体中，生长速度较快而不能自行消失，使得生长界面不稳定，这种因组分变化而产生的过冷现象被称为组分过冷，由此而形成的胞状组织使得晶体中溶质偏聚较为严重，因此需要通过改变工艺条件来控制组分过冷的出现。

从图2可以看出，当熔体内温度梯度增大到一定程度时(温度分布①)，温度分布曲线在生长界面处与凝固点变化曲线相切，熔体实际温度始终高于凝固点温度，因此不会出现组分过冷现象。考虑熔体中的对流输运，不产生组分过冷的临界条件为[17]：

(1)

式中:CL为熔体中溶质的平均浓度;D为溶质在熔体中的扩散系数;k0为溶质的分凝系数;δ为溶质边界层厚度;m为液相线斜率;V为晶体生长速度;G为生长界面处熔体的温度梯度。其中熔体对流对于组分过冷的影响主要体现在影响溶质边界层厚度δ上，对流强度越大，溶质边界层越薄。因此，为了避免组分过冷以及提高晶体质量，需尽量减小V/G，合理控制晶体生长速度V，并使界面前沿熔体的温度梯度G与其相匹配。

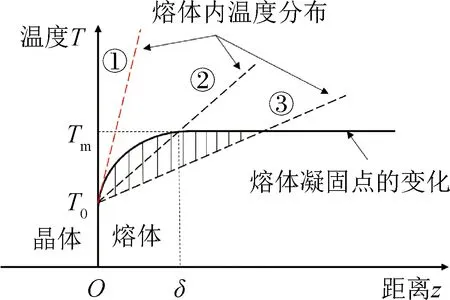
图2 熔体凝固点变化及组分过冷区的形成Fig.2 Solidification point and the formation of the subcooling zone of the composition

此外，为了保证凝固只发生在生长界面，硅熔体内部及表面不出现冷点，熔体温度必须高于凝固点温度，但是熔体的最高温度要控制在一个合理的范围内。这是因为温度过高会使化学反应速率加剧，杂质生成量增多，同时熔体过高的温度也增加了能耗。因此需要尽量减小硅熔体内部的温度差ΔT。

除了将V/G、q、Δh、ΔT作为评价铸锭晶体硅质量的准则，在实际生产过程中通常需要保证TC1温度在较小范围内变化以实现稳定的晶体生长。另外改变底部隔热笼开口以及侧、顶加热器功率比时，总功率P需随之做出一定调整以合理控制晶体生长速度。因此将这两个参数也作为研究对象，通过人工神经网络建立晶体生长工艺(底部隔热笼开口、侧、顶加热器功率比)与以上6个参数TC1、P、V/G、q、Δh、ΔT之间的映射关系，实现晶体生长过程中晶体质量参数与热场参数的快速预测，从而进一步理解工艺对于晶体质量的影响规律。

1.2 人工神经网络模型

人工神经网络是一种使用类似于大脑神经突触连接的结构进行信息处理的数学模型，其网络自身通常是对某种算法或函数的逼近。神经网络通常由输入层、输出层、隐藏层组成，其基本组成单位是神经元，而隐藏层中则包含若干非线性处理层，下面以一个2层神经网络(见图3)为例进一步说明其工作原理。

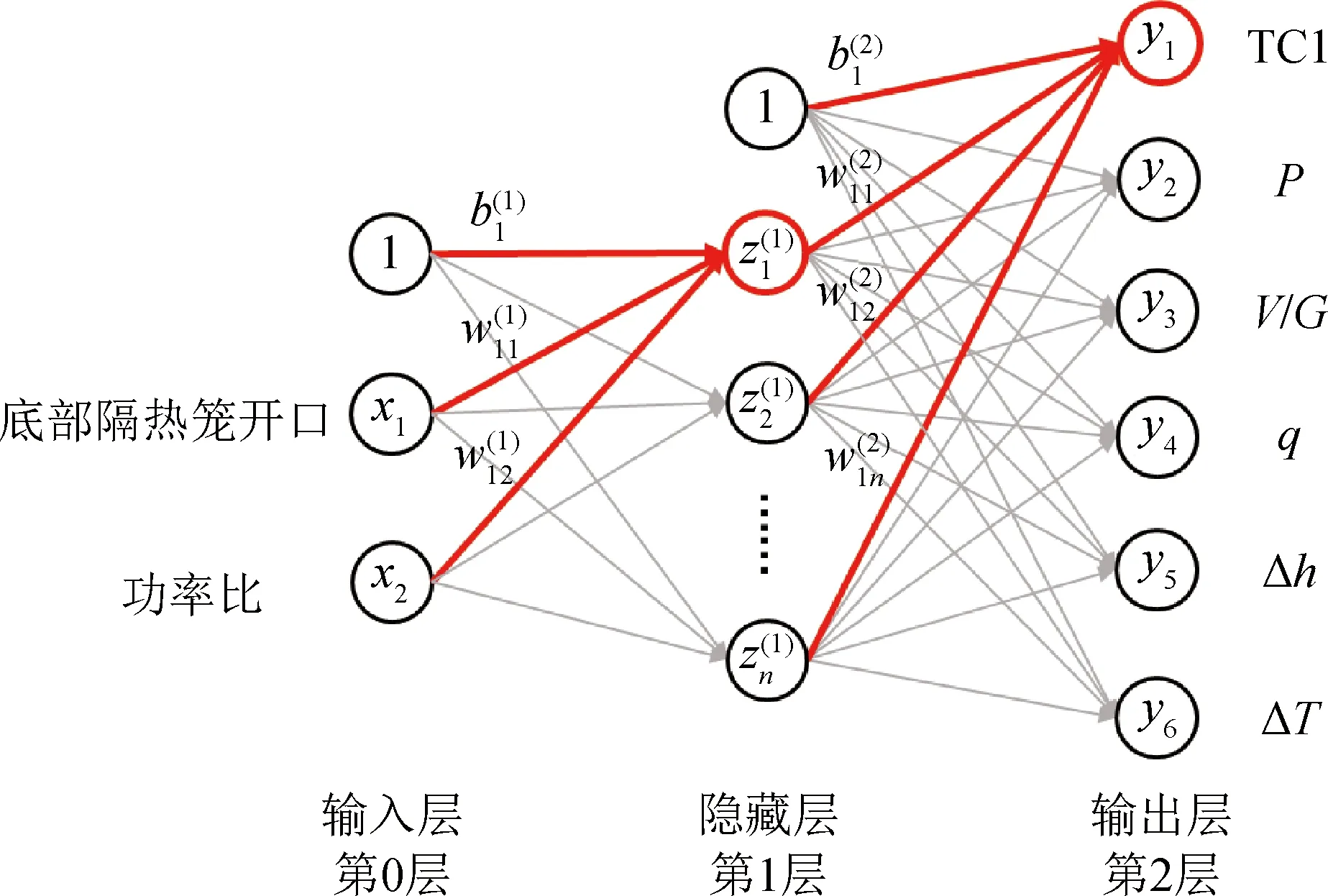
图3 2层神经网络示意图Fig.3 Schematic diagram of a two-layer neural network

对于晶体硅铸锭过程，选择底部隔热笼开口和功率比两个工艺控制参量为输入层的神经元，TC1、P、V/G、q、Δh、ΔT六个参数为输出层的神经元。在隐藏层中通过一系列非线性处理，建立输入与输出的映射关系。在神经网络中，各层的每一个神经元均为上一层所有神经元加权组合的函数，标有“1”的神经元为一偏置神经元，用于控制神经元被激活的容易程度[19]。现以第1层与第2层的第一个神经元为例表示其输出结果：

(2)

(3)

定义神经网络输出层的预测值与实际值之间的均方误差为损失函数：

(4)

神经网络的训练过程即为通过对大量数据进行运算，以减小损失函数为目标寻找最优的权重参数，并获得泛化能力，对于未观测过的新数据也能够做到准确预测，也就是说，神经网络能够学习到大量数据中隐含的内在规律。最基本的寻找最优参数的方法为随机梯度下降法(SGD)，沿损失函数关于参数的梯度方向不断更新参数，以W表示需要更新的权重参数矩阵，α为学习率，随机梯度下降法的表达式如下所示：

(5)

当损失函数减小到一定范围并保持稳定，可使用未包含在训练集中的数据对训练完成的神经网络进行检验，此即为神经网络的验证及测试过程。

本文采用Pytorch深度学习框架建立人工神经网络模型，通过反向传播算法训练神经网络，采用Adam[20]优化算法更新权重参数，为了提高运算速度以及避免在反向传播中出现梯度消失的问题，使用ReLU函数作为激活函数，由式(6)表示。为抑制过拟合以及降低结果对权重初始值的依赖性，在激活之前加入Batch Norm[21]层对数据分布进行正规化，使数据分布的均值为0、方差为1。

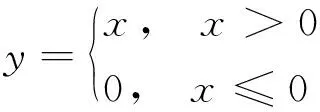
(6)

1.3 优化方法

本文的优化目标是减小或增大V/G、q、Δh、ΔT，是多目标优化问题。对于单目标优化问题，任何两个解都能够通过一个目标来评价其优劣，最终可以得到全局最优解。而在多目标优化问题中，经常会存在各目标间的冲突，一个解在某个目标上是最好的，但在其他目标上可能是最差的，因此很难找到一个能同时满足各目标要求的最优解。基于此，需引入多目标优化问题的合理解集：Pareto最优解[22]，即不比其他任何解差的解集。以一个双目标函数f1和f2的最大化为例说明Pareto最优解的概念，如图4所示，对于解x1和x2来说，f1(x1)>f2(x2) 但同时f2(x2)>f2(x1)，因此很难评价解x1和x2孰优孰劣。Pareto最优解集中的任意解相比于其他任何解都不处于劣势，即不存在更优的解，所以也将Pareto最优解称为非劣解。求得多目标优化问题的Pareto最优解集后，通常可以在解集的范围内依照经验选取符合问题需求的若干解。

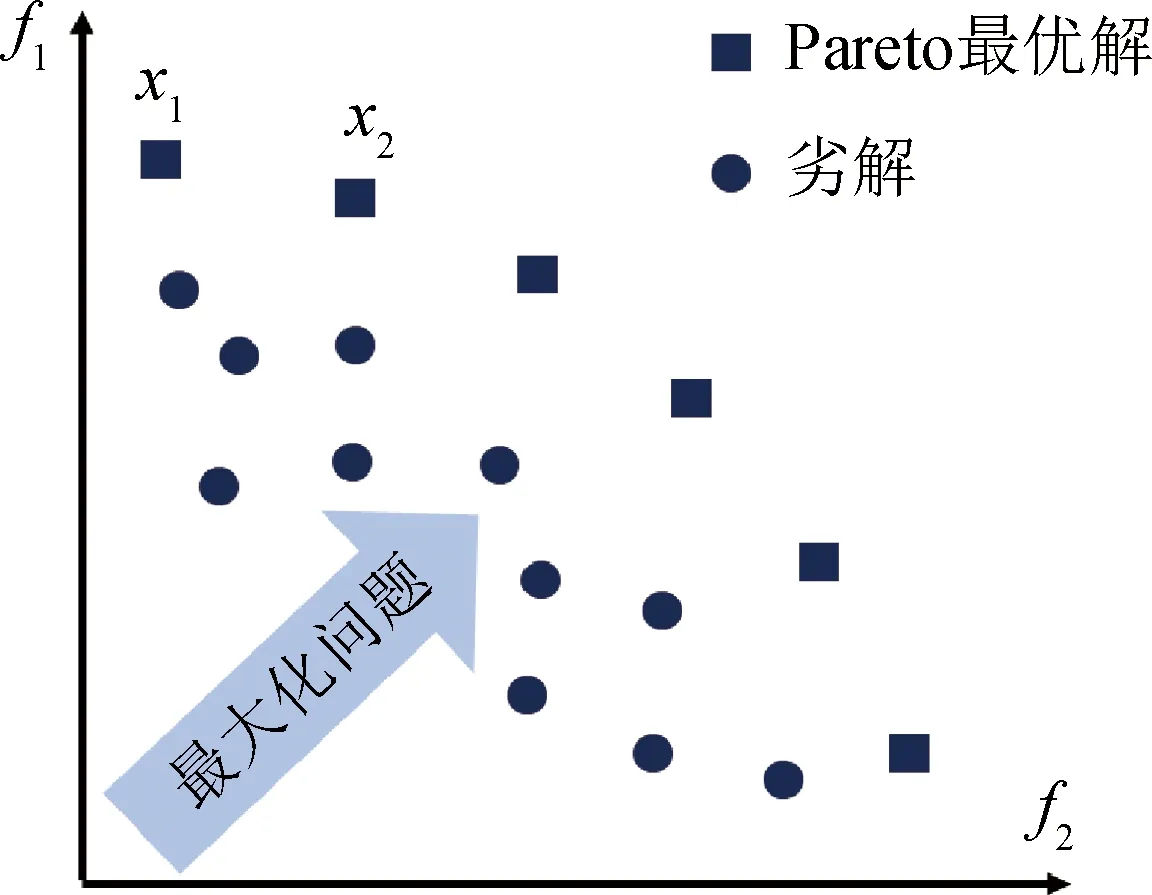
图4 一个双目标函数最大化问题的Pareto最优解示意图Fig.4 A schematic of the Pareto optimal solutions of a double-objective-function maximization problem

针对本文研究的多目标优化问题，采用遗传算法作为优化方法。遗传算法通过模拟自然进化过程来搜索一定范围内的最优解，从一个初始种群开始，经过多代选择、交叉、变异等演化行为，最终得到最适应当前环境(适应度高，即符合优化需求)的末代种群。首先对数据进行二进制编码，在各工艺参量的给定取值范围内随机产生一组初始候选解，并将其作为初代种群，随后经过一系列选择、交叉、变异等遗传操作逐步选出优化的工艺参量。图5所示为遗传算法与人工神经网络相结合的优化流程图。

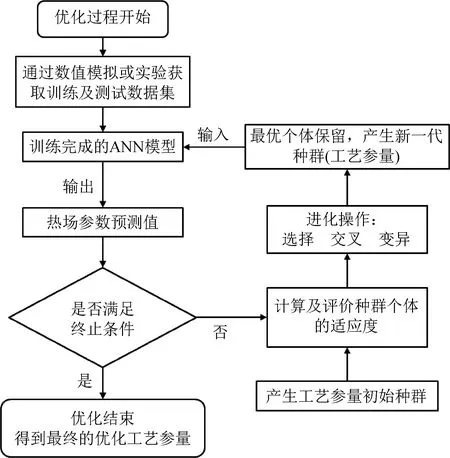
图5 神经网络结合遗传算法的优化过程Fig.5 Optimization process of ANN combined with GA

1.4 数据产生

建立人工神经网络模型所需要的大量数据来自数值仿真模拟预测和实验测量，实际生产和实验中所能测得的数据种类有限，难以满足研究需求，因此本文采用基于实际生产过程的数值仿真模拟获得不同工况下的V/G、q、Δh、ΔT等参量。由于晶体生长过程非常缓慢，流体运动较小，假设系统为准稳态、不可压流，同时将铸锭炉视为二维轴对称，对晶体硅生长过程的整场输运方程进行求解[23]，其中考虑热传导、热场各部件表面间的热辐射、结晶潜热、气体对流等。对于硅熔体部分，由于其流动非常微弱，为简化计算，流动对能量输运的影响通过考虑等效的热导率来计算。

根据底部隔热笼开口大小、功率比和总功率的不同，晶体生长高度也不同，数值模拟在几个特定隔热笼开口下采用一系列不同的功率比，通过不断调整总功率P以使晶体硅的中心高度达到预期高度。采用与实际生产中相近的功率比在底部隔热笼开口分别为70 mm、80 mm、85 mm、90 mm、95 mm时进行数值模拟，并将模拟得到的TC2温度与生产中测得的TC2温度进行对比，如图6所示，二者变化趋势相近，说明数值模拟能够较真实地反映实际生产过程。

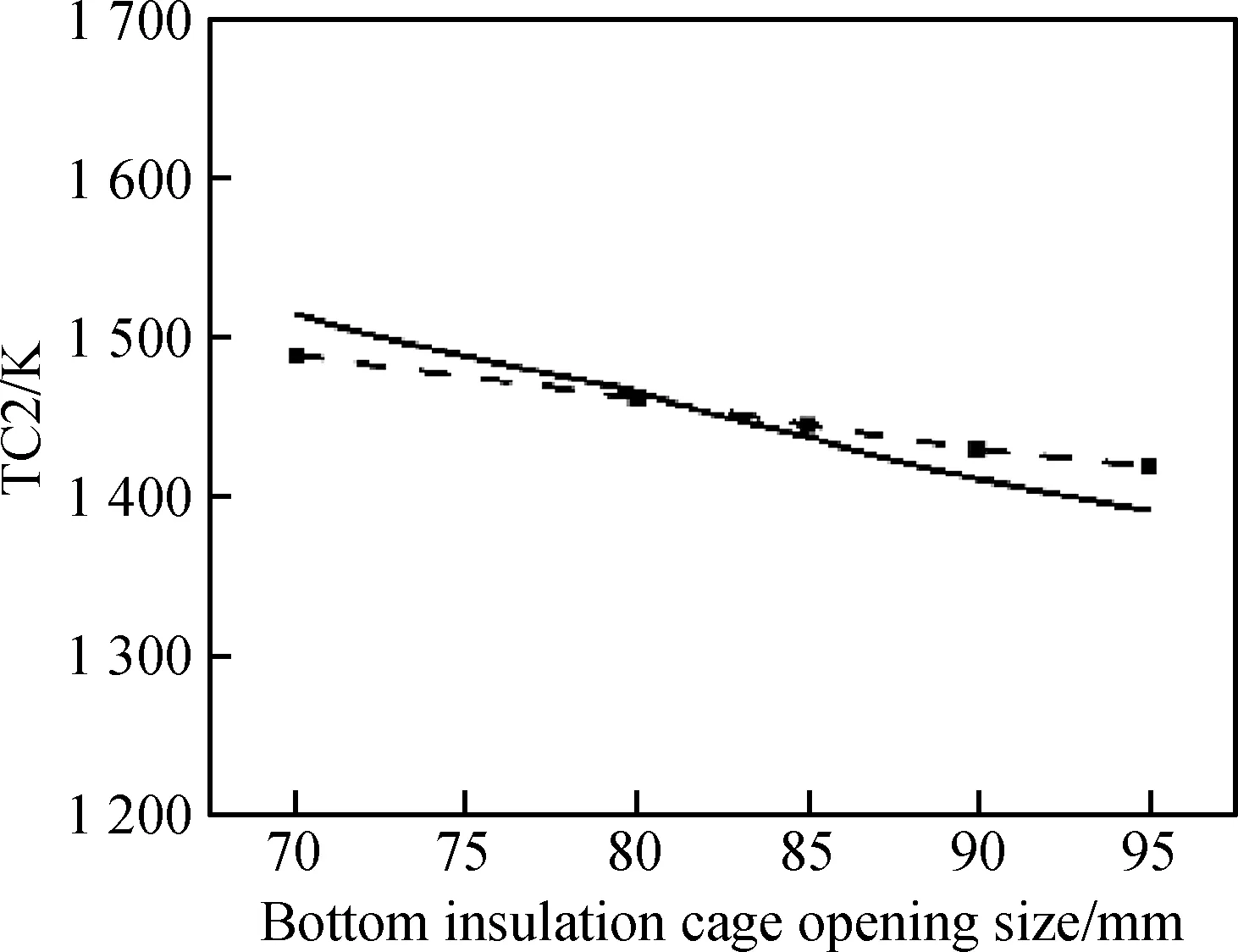
图6 晶体生长过程数值模拟(虚线)与实验(实线)的TC2温度对比Fig.6 TC2 comparison between numerical simulation (dash line) and experiment (solid line) during the crystal growth

对于需要进行研究的参量V/G、q、Δh、ΔT，本文假设在同一时刻生长界面上各点的生长速度V相等，将生长界面各点的V/G平均值作为该工况的V/G值。监测生长界面与坩埚接触处的壁面热流，热流方向以从坩埚流向硅区域为正。根据大量数值仿真模拟的结果，|q|<100左右时生长界面边缘形状较为平直，q很小(负值)或很大(正值)时则分别呈现过凹或过凸的形态。生长界面的高度差Δh定义为中心高度与边缘高度之差，为方便之后的工艺优化过程，在计算过程中q与Δh均取其绝对值。对于硅熔体温度差，则通过监测硅熔体内部的最高温度来获得。通过前面的分析可以得出，减小晶体生长过程中的V/G、|q|、|Δh|、ΔT，可以提高晶体质量。

2 结果与讨论

基于上述人工神经网络和遗传算法在铸锭晶体硅中的参量选择原则，下面分别介绍如何通过已有的数据建立工艺参量与晶体硅质量参数之间的神经网络映射模型，将其作为遗传算法的数据来源，实现晶体生长过程中工艺控制参数的优化，最后基于实际生产中硅锭的检测数据，研究V/G对于晶体生长过程及其质量的影响和控制策略。

2.1 人工神经网络模型的建立

根据实际生产过程及其工艺选取5个典型的隔热笼开口，分别为70 mm、80 mm、85 mm、90 mm、95 mm，功率比在1～4范围内取值，通过调整总功率P使得在相同的隔热笼开口下生长界面中心达到同一高度，从相应模拟结果中计算得到TC1、V/G、|q|、|Δh|、ΔT，通过多次数值模拟得到76组数据，对于神经网络输入数据(隔热笼开口、功率比)作min-max归一化处理，即对原始数据进行线性变换，使其映射到[0,1]之间。对于输出数据(TC1、P、V/G、q、Δh、ΔT)则采用z-score归一化，使经过处理的原始数据符合标准正态分布。为减小训练难度，将其概率分布在标准正态分布基础上平移至均值为2。经过归一化处理的76组训练数据采用五折交叉验证法进行神经网络模型的调优，寻找能使神经网络泛化性能最优的超参数值，其中超参数即为神经网络中需要人为给定的网络结构参数，如隐藏层层数、各层神经元个数、学习率等。五折交叉验证法的示意图如图7所示，将训练数据集随机分成五等份，每次取其中一份作为验证集，其余4份作为训练集，这样循环五次作为一次交叉验证，通过多次交叉验证来寻找合适的超参数值，由于采用了无重复抽样技术，每次交叉验证过程中每组数据只有一次被划入训练集或验证集的机会。另外，再通过多次数值模拟得到14组不包含在训练数据内的数据作为独立测试集，用于测试模型的泛化性能。

经过多次交叉验证，找到合适的超参数值，采用2层隐藏层，每层各128个神经元，初始学习率设定为0.01，并随着训练过程的进行不断减小。使用该网络结构进行的五次迭代过程损失函数变化如图8所示，可以看到验证集的损失函数值稳定在0.01，训练集损失函数稳定在1×10-3与1×10-4之间，根据训练集与验证集划分方式的不同，训练过程和结果均有一定的差异，但从图中可以看出五次交叉验证的结果相差不大。五个不同验证集TC1、P、V/G、q、Δh、ΔT的平均相对误差E分别为：4.99%、2.53%、4.80%、4.60%、7.23%、2.56%。然后在全部训练数据集上重新训练模型，并使用独立的测试集对模型性能做出最终评价，得到6个参数预测结果的平均相对误差分别为：1.49%、1.44%、2.99%、1.39%、2.66%、1.58%。因此可以认为该神经网络能够在本文给定范围内较准确地预测热场特性，并具有一定的泛化能力。使用该神经网络计算并输出1组热场参数仅需0.01 s(使用1个2.90 GHz CPU，单线程)，若采用数值仿真模拟则大约需要183 s(使用1个2.90 GHz CPU,3线程)。

图7 五折交叉验证法示意图Fig.7 Diagram of five-fold cross-validation

图8 五次交叉验证过程训练数据(实线)及验证数据(虚线)的损失函数变化情况Fig.8 Changes in the loss function of the training (solid line) and validation data (dash line) during five-fold cross-validation process

图9显示在底部隔热笼开口分别为70 mm、85 mm和95 mm时使用该神经网络的预测值分析功率比对晶体生长过程热场的影响规律，其中纵坐标为经过z-score归一化以及概率分布平移处理后的值。在底部隔热笼开口大小不同时，各参量随功率比的变化规律均有一定的改变，但整体上仍然有共同点。在同一个隔热笼开口下，随着功率比的增大，顶加热器功率逐渐减小，侧加热器功率逐渐增大，熔体中的温度梯度减小，V/G持续增大，ΔT则先减小后增大。随着底部隔热笼开口增大，V/G整体上有下降趋势，ΔT的变化幅度也逐渐减小。|Δh|和|q|的变化图线显示，随着功率比增大，生长界面由凹变凸，生长界面与坩埚壁接触处也由凹变凸，然而需要注意的是隔热笼开口70 mm时，在功率比变化的全范围内生长界面边缘呈现下凹的形态，这是因为侧加热器与坩埚底部有一定的距离，在隔热笼开口较小时，较小的晶体生长高度使得热量容易从没有侧加热器遮挡的坩埚侧壁部分散出，导致了该处生长界面下凹。

从图9(a)～(c)也可以看到，由于各参量变化趋势不同，因此很难找到能使V/G、|q|、|Δh|、ΔT同时达到最小的功率比，这也就说明了多目标优化中的最优解集并非指绝对最优解，而是在各参量间做出取舍之后的相对最优解。

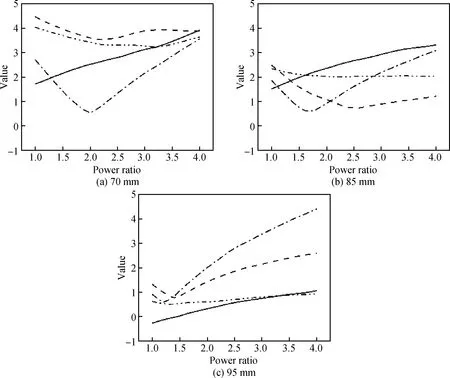
图9 不同底部隔热笼开口下的热场参数V/G(实线)、|q|(虚线)、|Δh|(点划线)、ΔT(双点划线)随功率比的变化情况Fig.9 Dependences of thermal field parameters V/G (solid line), |q| (dash line), |Δh| (dot dash line), ΔT (double-dot dash line) on power ratio, at different bottom insulation cage opening sizes

2.2 遗传算法对工艺控制参数的优化

本文的优化目标为减小V/G、|q|、|Δh|、ΔT。工艺的优化需保证在晶体生长过程中TC1变化幅度较小，以实现晶体的稳定生长，另外需要使晶体生长界面高度差Δh为正并且尽量接近0，以得到微凸的界面。设定种群规模为20，即每一代进化中都有20组决策变量，分别固定底部隔热笼开口为70 mm、80 mm、85 mm、90 mm、95 mm，功率比则在取值范围内进行随机初始化，经过5 000代进化后，决策变量由随机分布逐渐聚集，5次进化结果如图10所示，在每次进化中聚集的点集即为相应工况下的Pareto最优解集，即不比其他任何解更差的非劣解集。由于多目标优化中各目标之间的冲突性，很难同时使四个热场参数同时达到最优，而且由于实际晶体生长过程工艺参数调整需有连续性，不能在Pareto最优解集中随意选择工艺参数。因此按照以下准则从各Pareto最优解集中选取一系列优化的功率比：①使Δh为正且尽量接近0；②减小|q|且尽量使|q|<100；③在不同的隔热笼开口下TC1变化幅度较小。优化前(虚线)、后(实线)的工艺参数变化如图11所示，初始工艺的功率比始终为3，优化工艺的功率比则在2附近波动，先增大后减小；总功率整体上小于初始工艺，从而降低了能耗；优化工艺的TC1变化幅度也小于初始工艺。

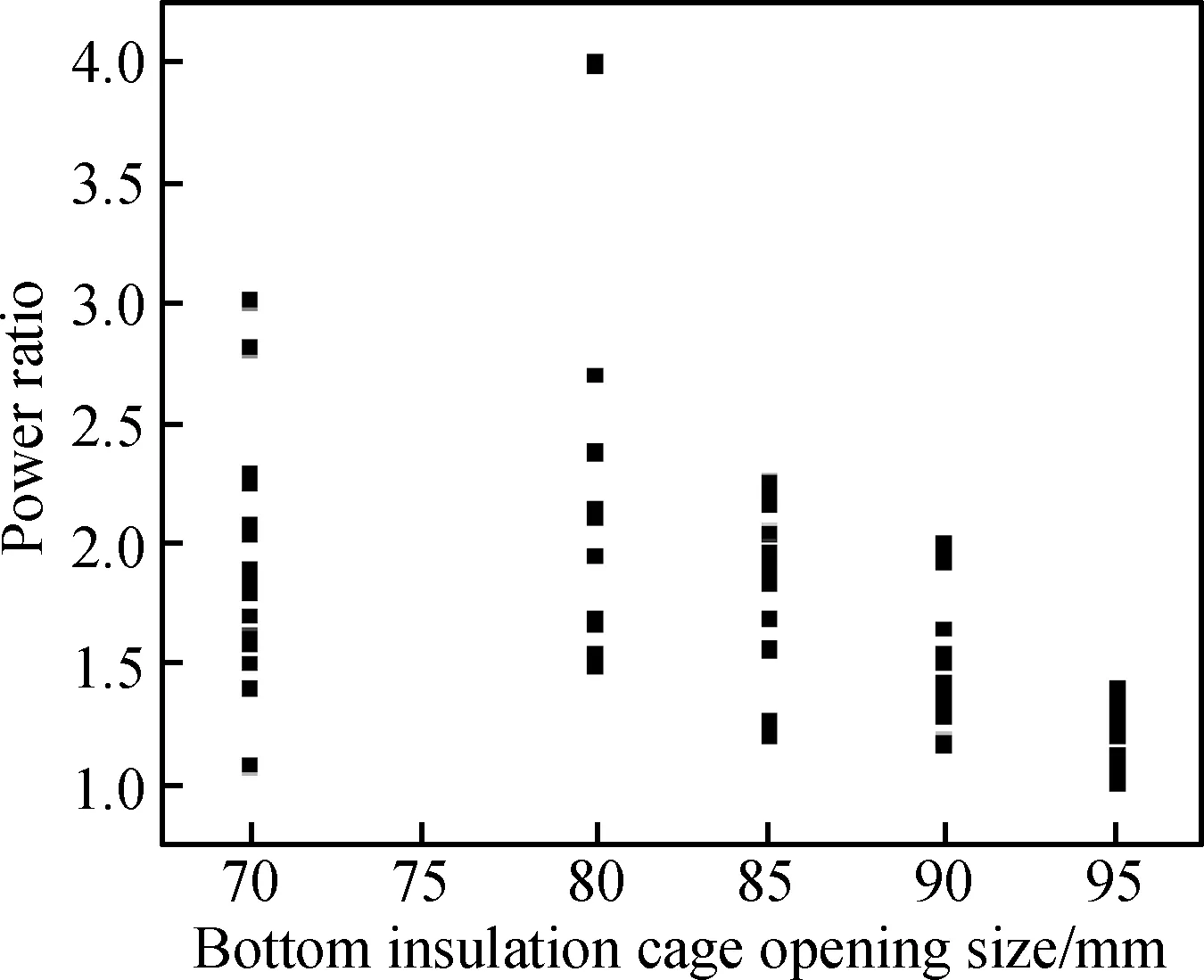
图10 使用遗传算法进化5 000代后的Pareto最优解集Fig.10 Results after 5 000 generations of evolution using genetic algorithm

通过数值模拟求解相应热场，计算得到热场参数，并与初始工艺的热场参数值进行比较，如图12所示。由1.4节可知减小晶体生长过程中的V/G、|q|、|Δh|、ΔT，可以提高晶体质量。优化工艺的(a)V/G和(c)生长界面高度差Δh在该晶体生长范围内均小于初始工艺的相应值；(b)壁面热流q在除隔热笼开口80 mm之外的工况，其绝对值均小于初始工艺的相应值；优化工艺得到的(d)硅熔体温差ΔT则在该晶体生长范围的前半段略大于初始工艺，后半段略小于初始工艺。由于优化工艺的功率比小于初始工艺，侧加热器功率减小，顶加热器功率相对增大，硅熔体内的温度梯度增加，在本文中晶体生长速度V相同的情况下，V/G减小；坩埚侧壁温度略有降低，晶体生长前期界面边缘过凹以及后期界面过凸的问题也得以改善；优化过程并不涉及铸锭炉结构和晶体生长速度的改变，优化前后硅熔体温差变化不大，因此不将此参量作为影响晶体硅质量的主要因素。晶体生长过程中不同阶段的界面随底部隔热笼开口大小变化如图13所示，R表示从界面中心到界面边缘的坐标，z表示界面高度，可以看到优化后的晶体界面趋于平直，且在晶体生长前期界面边缘的下凹程度得以减轻。因此综合来看，优化后的工艺实现了晶体质量的提高，并减小了总功率。

图11 优化前(虚线)及优化后(实线)的(a)功率比、(b)总功率和(c)TC1分别随底部隔热笼开口的变化Fig.11 Before (dash line) and after (solid line) optimization for the response of (a) power ratio, (b) total power and (c) TC1 to the bottom insulation cage opening size, respectively

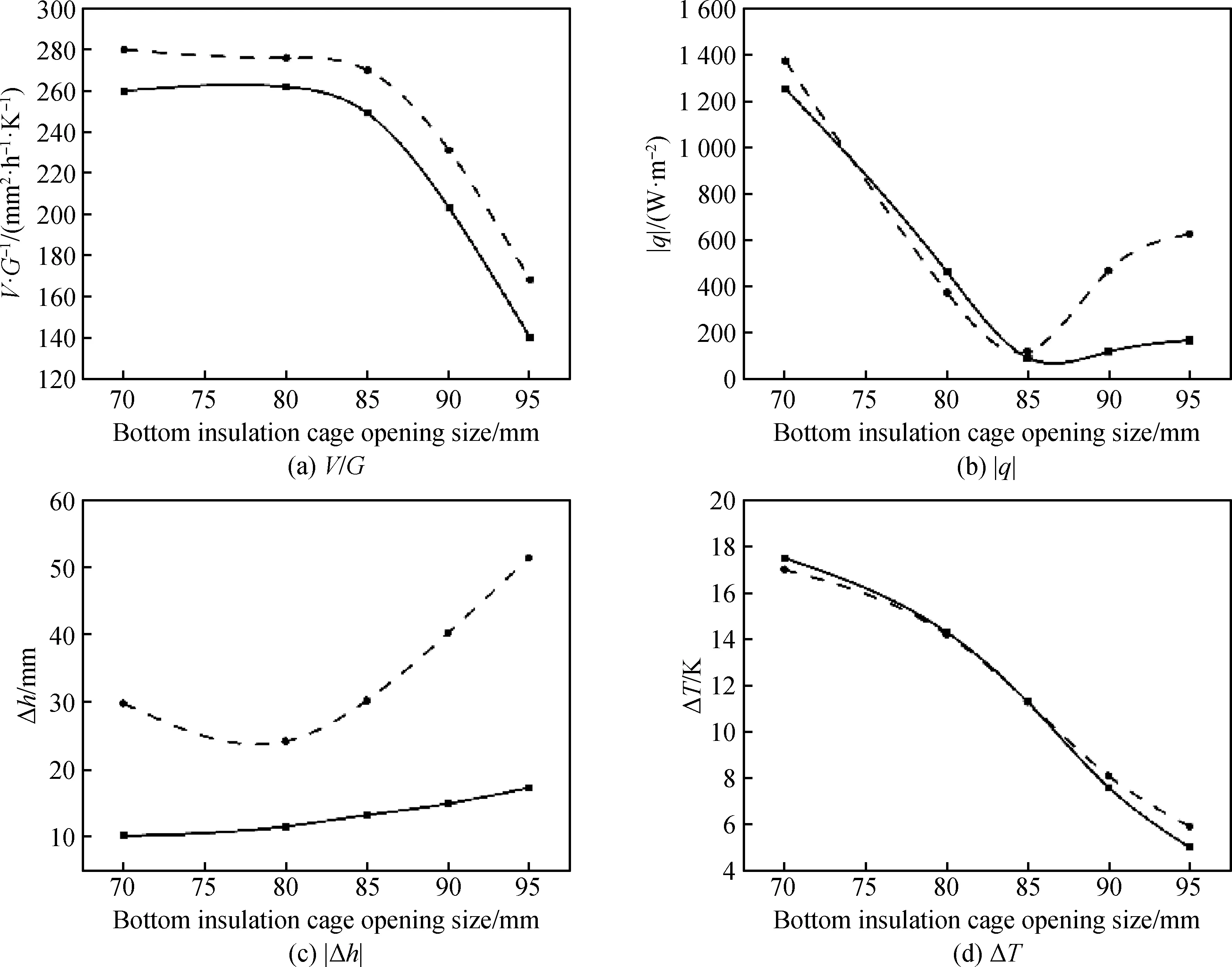
图12 优化前(虚线)及优化后(实线)热场参数随底部隔热笼开口的变化Fig.12 Before (dash line) and after (solid line) optimization for the response of thermal field parameters to the bottom insulation cage opening size, respectively

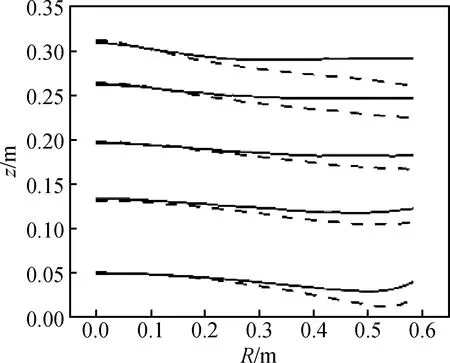
图13 优化前(虚线)及优化后(实线)的晶体生长界面位置z的变化Fig.13 Crystal growth interface location z before (dash line) and after (solid line) optimization

2.3 V/G的横向分布对晶体质量的影响

铸锭晶体硅的生长速度V呈现前期快、后期慢的趋势，参考实际生产过程，本文采用如图14(a)所示的晶体生长速度随时间变化曲线，底部隔热笼开口随时间变化曲线如图14(b) 所示。从图12(a)可以看到生长界面上的平均V/G初始变化平缓，在晶体生长中后期则迅速减小，一方面因为后期晶体生长速度减慢，另一方面则是由于熔体高度不断减小，熔体内温度梯度增大的缘故。下面给出使用优化前后工艺在不同生长高度时界面上的V/G分布曲线，如图15所示，优化后的工艺使得V/G在整体上减小的同时，在横向上的分布也更加均匀。在晶体生长前期(h=50 mm)，生长界面边缘均出现V/G的突增，这与换热台四周添加的一圈保温棉有关，使得生长界面边缘的温度梯度较小。在晶体生长中期(h=131 mm,h=194 mm)，从界面中心到界面边缘的V/G变化趋于平缓，而在晶体生长后期(h=264 mm,h=311 mm)，界面中心的V/G明显大于界面边缘，且随晶体生长的进行，差值逐渐增大。

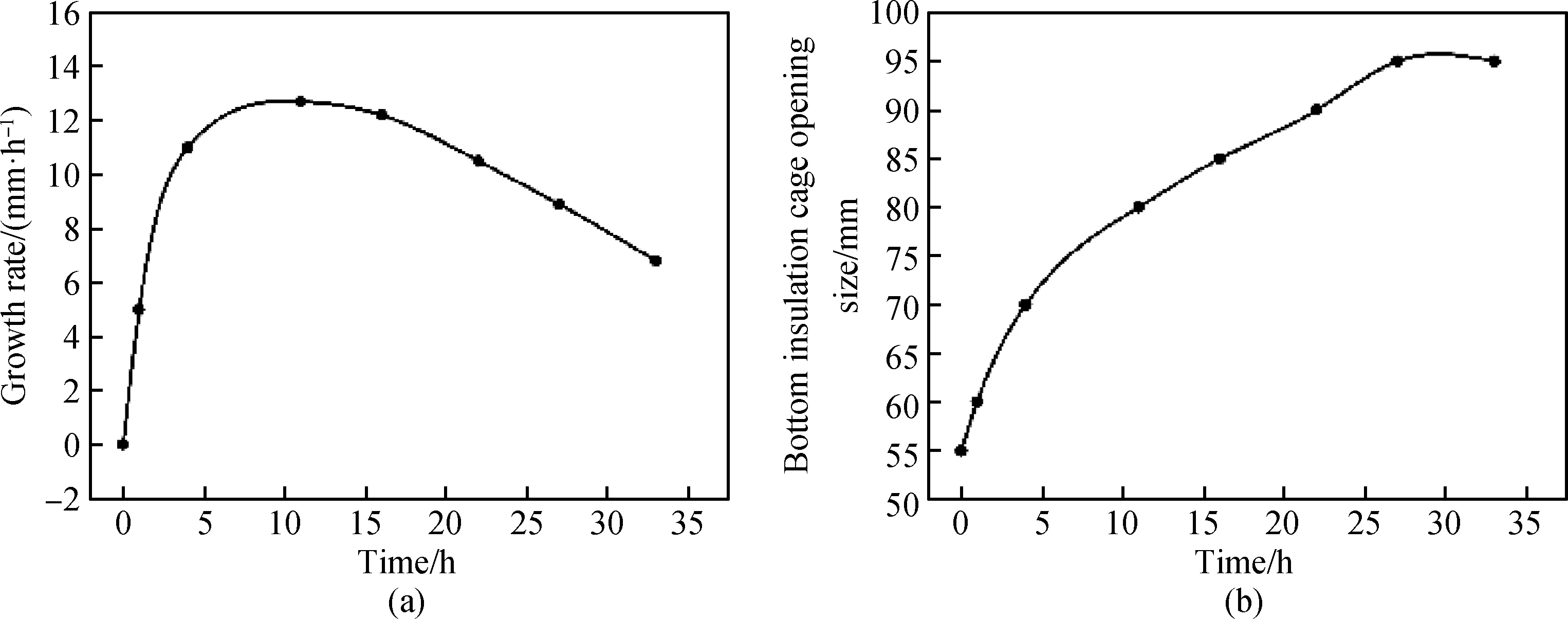
图14 (a)晶体生长速度和(b)底部隔热笼开口随时间的变化Fig.14 Variations of (a) crystal growth rate, and (b) the bottom insulation cage opening size with time, respectively

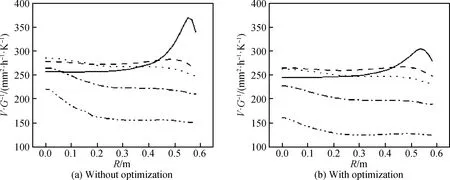
图15 不同晶体生长高度h=50 mm(实线),h=131 mm(虚线),h=194 mm(点线),h=264 mm(点划线), h=311 mm(双点划线)时界面V/G沿径向的分布Fig.15 Interface V/G distribution along the radial direction at the crystal growth height, h of 50 mm (solid line), 131 mm (dash line), 194 mm (dot line), 264 mm (dot dash line), 311 mm (double-dot dash line), respectively

为了进一步研究V/G对晶体生长过程的影响，对切除边皮并开方后的硅锭侧面进行光致发光(PL)检测及少子寿命检测。图16(a)为PL检测图，其中的阴影区表示缺陷，每个小锭下方标出的数字即为缺陷面积占检测面积的百分比。从硅锭中心到两侧边缘缺陷面积占比逐渐增多，但分布并不完全对称，边缘处的阴影线从侧面倾斜向上，此即为硅熔体与冷壁接触，因异质形核产生的随机取向多晶区，也导致了相应的缺陷。对硅锭端面进行PL检测，如图17所示，硅锭边缘的缺陷面积较大，通过控制壁面热流q可以抑制边缘多晶向中心扩展，减小边缘的缺陷区，从而提高硅锭的质量以及利用率。

图16(b)为少子寿命检测图，红色区域为低少子寿命区，金属杂质含量较多，相应也存在大量缺陷，晶体生长高度h=50 mm即位于硅锭尾部的大阴影区内，随着晶体生长的进一步进行，缺陷数量减少且分布较为均匀，对应于晶体生长中期(h=131 mm,h=194 mm)的V/G变化也较为平缓。而在晶体生长后期，虽然V/G整体上减小了，但从PL检测图中可以看到缺陷再次增多，这说明随着熔体不断减少，杂质在熔体中不断富集，其他因素对于晶体硅质量的影响更大，而这也是需要进一步探究的问题，同时硅锭中心的阴影区有增大的趋势，这与前面提到的V/G在界面中心大于界面边缘的变化规律相符合。因此除了减小V/G，增加其在横向上的均匀度也是提高晶体质量的重要因素。

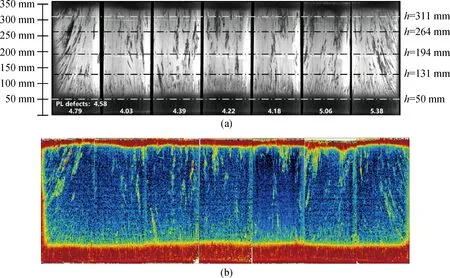
图16 硅锭侧面的(a)PL检测图,(b)少子寿命检测图Fig.16 (a) PL inspection image, (b) minority carrier lifetime inspection image on the side of the silicon ingot

图17 硅锭端面的PL检测图Fig.17 PL inspection diagram of silicon ingot end face

3 结 论

本文基于数值模拟与实验数据建立了工艺控制参数与影响晶硅质量的热场参数之间的神经网络模型，并结合遗传算法以减小V/G、|q|、|Δh|、ΔT为目标优化工艺控制参数。训练完成的神经网络能够做出快速且较准确的预测，4个热场参数测试结果的平均相对误差分别为： 2.99%、1.39%、2.66%、1.58%，且该神经网络映射模型使不同工况下的热场参数计算速度相比数值仿真模拟大大提升。将神经网络作为遗传算法搜索的数据来源，根据底部隔热笼开口大小不同选取5个典型工况，分别对其功率比进行优化，在进化5 000代后得到的Pareto最优解中选取符合需求的工艺参量进行数值模拟，优化后V/G、|q|、|Δh|基本上在该晶体生长范围内实现减小，在一定程度上提高了晶体质量，并且减小了总功率，从而降低了能耗。

最后结合实际生产中硅锭的PL检测图和少子寿命检测图分析了V/G对晶体质量的影响。在晶体生长中期V/G沿径向变化较为平缓，对应缺陷相对较少且分布均匀，因此增加V/G在横向上的均匀度也是提高晶体质量的重要因素，晶体生长前期及后期出现的大量缺陷则受杂质等其他因素影响更大。硅锭边缘的缺陷主要产生于随机取向多晶区，通过控制壁面热流q可以抑制边缘多晶向中心扩展，提高硅锭的质量和利用率。

本文采用经过实验数据验证的数值模拟结果建立人工神经网络模型，优化结果也通过数值模拟进行了对比验证，后续的研究计划是通过理论结合实验，进一步验证优化工艺的可行性，并用于指导实际生产。除了热场方面，晶体硅生长过程中的氩气流场与杂质输运过程对于晶体质量来说也至关重要，且目前尚无铸锭晶体硅的生长界面探测技术与反馈控制，如何将机器学习方法应用于此，也需要进行进一步的研究。