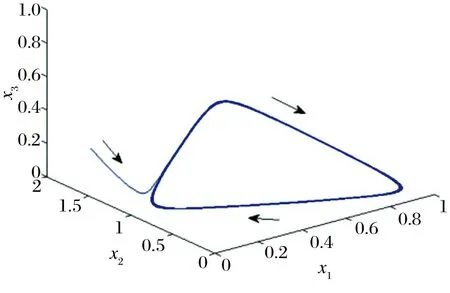
三种系统非线性微分方程的奇点分析与模拟
2022-04-13耿杰
耿 杰
(安徽信息工程学院 通识教育与外国语学院, 安徽 芜湖 241000)
通过常微分方程的理论,可以发现在局部的定性分析中,非线性系统在正常点附近的轨线结构是一般的, 但在奇点附近会出现复杂的情况, 也因此奇点成为了非线性系统定性理论中一个非常重要的研究对象[1]. 奇点的稳定性和极限环的存在性对于其他各个学科的研究都有一定的帮助, 例如经济学(经济增长模型)、 生物学(捕食模型)等[2]. 这就需要对非线性微分方程的奇点的稳定性和极限环的存在性及唯一性有一定的了解[3]. 本文通过奇点与极限环的特性与定理分别建立二次系统、 三次系统与三维系统的数值模型, 验证微分方程奇点稳定性与准确性.
1 奇点与极限环的概述
1.1 奇点与极限环的概念
(1)奇点的概念
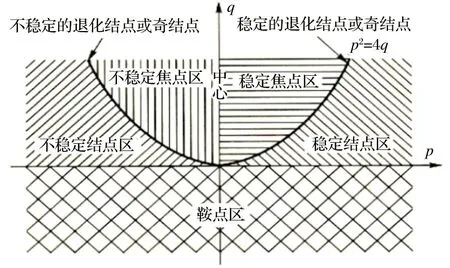
图1 奇点的类型和特征方程根之间的关系图
(2)极限环的概念与判别方法
孤立的闭轨线称为极限环. 如图2所示.
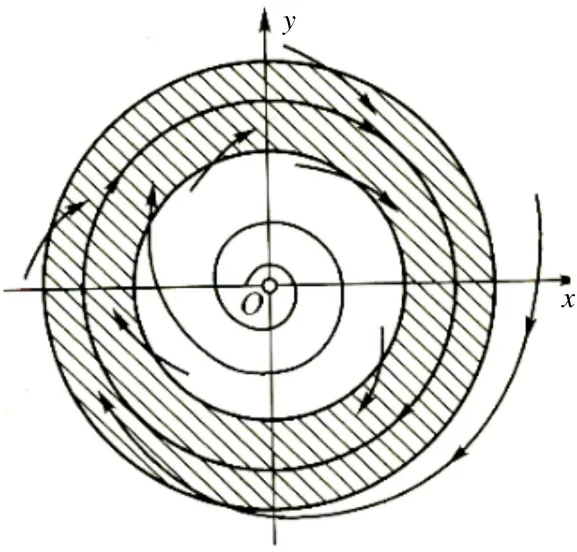
图2 极限环
当极限环附近的轨线均正向(即时)趋近于它时, 称此极限环是稳定的; 如果轨线是负向(即时)趋近此极限环, 则称它是不稳定的. 当此极限环的一侧轨线正向趋近于它, 而另一侧轨线负向趋近于它时, 称此极限环是半稳定的.
1.2 解的稳定性与极限环的存在性
(1)二次系统的奇点与极限环
文献[4]研究了如下二次系统:
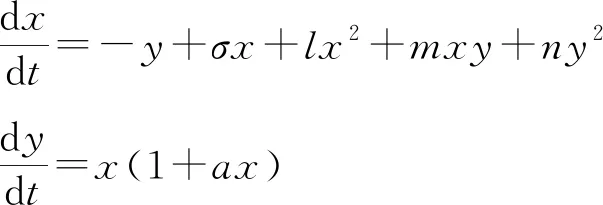
(1)
其中a>0,σ,l,m,n为实数. 可以很清晰地看出, 系统(1)的一次线性近似方程的系数矩阵为
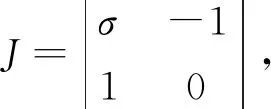
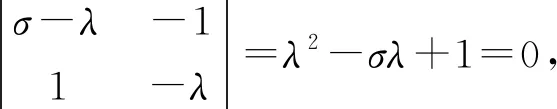
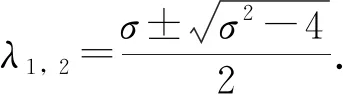
定理1当σ<0时, 零解(奇点)是渐近稳定的; 当σ>0时, 零解(奇点)是不稳定的.
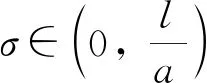
文献[5]研究了如下二次系统:
(2)
其中aij,c均为常数. 系统(2)在奇点O(0, 0)的一阶线性近似方程组的系数矩阵为
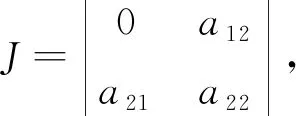
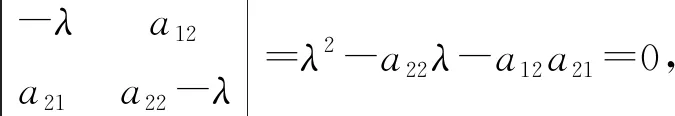
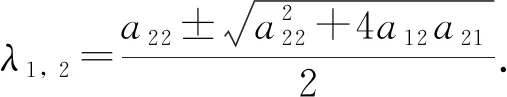
定理3考虑系统(2), 那么
(ⅰ)当a22<0,a12a21<0时, 系统(2)的奇点O(0, 0)渐近稳定;
(ⅱ)当a22>0,a12a21<0时, 奇点O(0, 0)是不稳定的.
对于系统(2)的极限环存在性及个数问题, 通过一定的计算分析, 得到如下结论:
定理4[5]如果a12=0或c=0,a22≠0, 则系统不存在围绕原点的极限环.
定理5[5]如果a12+a21=0,a22+ca21<0,a21<0,c>0,a22>0, 则系统围绕原点的极限环最多只有1个.
文献[5]还研究了二次系统:
(3)
其中aij,β均为常数. 这里, 可以清晰地看出, 系统(3)的一阶线性近似方程组的特征方程是
(a22+a12a21)=0,
系统特征根:
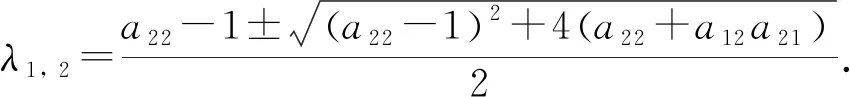
定理6当a22+a12a21<0,a22<1时, 系统(3)的零解渐近稳定; 当a22+a12a21<0,a22>1时, 零解是不稳定的.
关于系统(3)的极限环存在性问题, 通过计算以及分析, 给出了如下定理:
文献[6]研究了如下二次系统.
(4)
经过分析, 得到了如下结论:
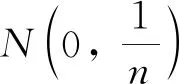
(2)三次系统的奇点与极限环
文献[7]研究了如下三次系统:
(5)
其中A0>0,A1≥-1,A1,A2,A3不等于零. 经过分析, 得到了如下结论:
定理8[7]考虑系统(5), 那么
(ⅰ)O(0, 0)是系统(5)的鞍点;
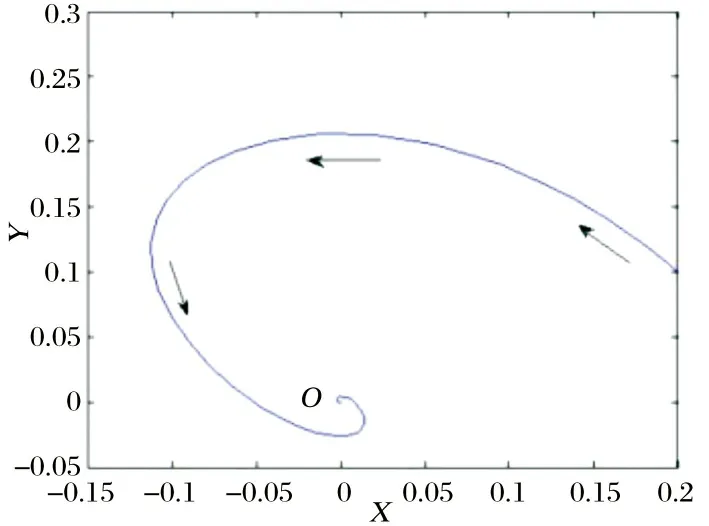
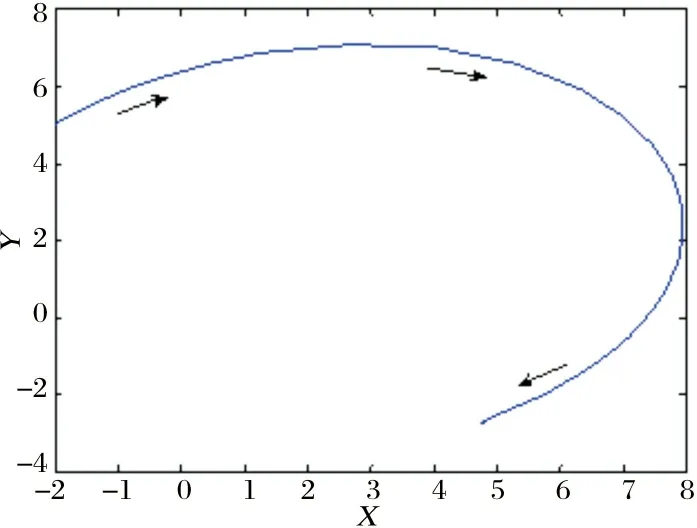
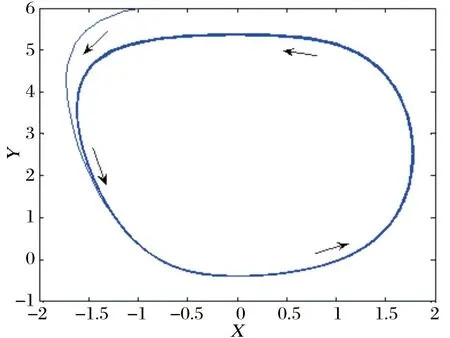
(ⅱ)当-1 文献[8]研究了如下三次系统: (6) 通过计算分析, 对于极限环的存在性问题得到了如下结论: 文献[9]研究了如下系统: (7) 其中c≠0. 经过分析, 得到了如下结论. 定理11[9]设b=0, 当ac≥0时, 系统(7)不存在极限环; 当ac≤0时, 系统(7)存在唯一极限环, 且当a>0时是稳定的, 当a<0时是不稳定的. (3)三维系统的奇点与极限环 文献[10]研究了如下三维二次系统: (8) 经过分析, 得到了如下结论: 考虑文献[4]二次系统(1), 即 (9) 其中a>0,σ,l,m,n为实数. 在系统(9)中, 令a=2,σ=-1,l=0.5,m=1,n=0.8, 则有a>0,σ<0, 即满足定理1的条件. 依定理, 系统(9)的奇点O(0, 0)是渐近稳定的. 通过MATLAB软件计算, 知O(0,0)是渐近稳定的, 如图3所示. 图3 系统(9)奇点 考虑文献[5]二次系统(3), 即 (10) 其中a12,a21,a22,β为常数. 在系统(10)中, 令a12=1,a21=-2,β=0.25,a22=2, 则满足定理7的条件, 依据定理, 系统(10)不存在极限环, 通过MATLAB软件计算分析, 该数值下系统(10)不存在极限环, 如图4所示. 图4 系统(10)极限环 考虑文献[8]三次系统(6), 即 (11) 在系统(11)中, 令β=-1,ζ=1,l=0.5,α=-0.8, 则满足定理10的条件, 依据定理, 系统(11)存在唯一的极限环, 并且是稳定的极限环. 通过MATLAB软件计算, 该数值下存在极限环, 如图5所示. 图5 系统(11)极限环 考虑文献[10]三维系统(8), 即 (12) 在系统(12)中, 令α=1.5,β=0.5, 则α+β=2, 即满足定理9的条件, 则系统(12)存在极限环. 运用MATLAB软件计算分析, 该数值下系统(12)存在极限环, 如图6所示. 图6 系统(12)极限环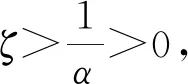
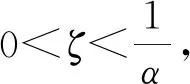
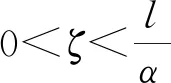
2 MATLAB数值模拟分析
2.1 二次系统数值模拟
2.2 三次系统数值模拟
2.3 三维系统数值模拟