基于Weibull型分布的最大和最小次序统计量矩计算
2022-04-13钟韵宁
钟韵宁
(福建师范大学 数学与信息学院, 福建 福州 350117)
次序统计量是数理统计中一类常用的统计量, 它不独立, 服从的分布也不相同。在任意总体分布上次序统计量的相应高阶矩计算存在一定的复杂性. 对于t分布[1]、 数正态分布[2]、 伽玛分布[3]、 卡方分布[4]的次序统计量矩计算已经有学者作出了一定的推导, 本文思考了一个双参数韦布尔(Weibull)分布. 该分布在可靠性系统分析中具有不可缺少的地位, 通常应用于各种产品材料的磨损累计的失效分布与器件设备的使用寿命等方面[5], 这些都是人们比较关注的问题. 并进一步对该分布总体的最大最小次序统计量、 样本极差和样本中位数作了一些分析, 推导出了相应的高阶原点矩的计算公式.
Weibull分布的分布函数[6-7]表示为
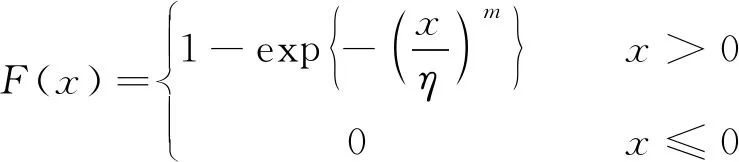
密度函数表示为
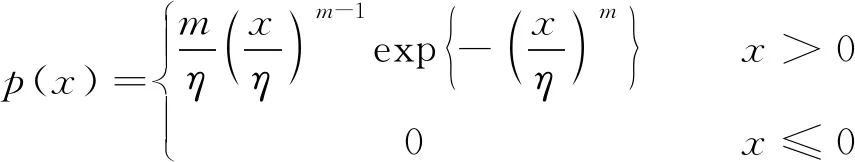
其中x是随机变量,m>0是形状参数,η>0是尺度参数(比例参数).
当m=1时, 它是指数分布; 当m=2时, 它是Rayleigh分布.
1 引理
引理1设总体分布为Weibull 分布,X1,X2, …,Xn为其样本,X(i)称为该样本的第i个次序统计量, 它的取值是将样本X1,X2, …,Xn从小到大排列后得到的第i个值,i=1, …,n. 则
X(n)=max{X1,X2, …,Xn} 的密度函数表示为
pX(n)(z)
X(1)=min{X1,X2, …,Xn} 的密度函数表示为
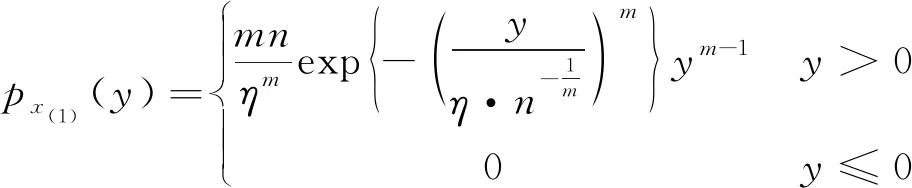
证明
记X(n)=max{X1,X2, …,Xn}, 令X(n)Z,
当z>0时, 由分布函数的定义有
FX(n)(z)=Pr(Z≤z)=Pr(max{X1,X2, …,Xn}≤z)=Pr(X1≤z,X2≤z, …,Xn≤z)

当z≤0时,FX(n)(z)=0.
即X(n)的分布函数表示为

所以X(n)的密度函数表示为
pX(n)(z)
记X(1)=min{X1,X2, …,Xn}, 令X(1)Y,
当y>0时, 由分布函数的定义有
FX(1)(y)=Pr(Y≤y)=Pr(min{X1,X2, …,Xn}≤y)=1-Pr(min{X1,X2, …,Xn}>y)
=1-Pr(X1>y)·Pr(X2>y)…Pr(Xn>y)
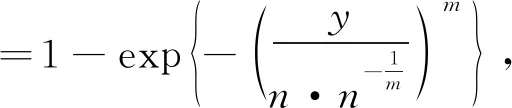
当y≤0时,FX(1)(y)=0.
即X(1)的分布函数表示为
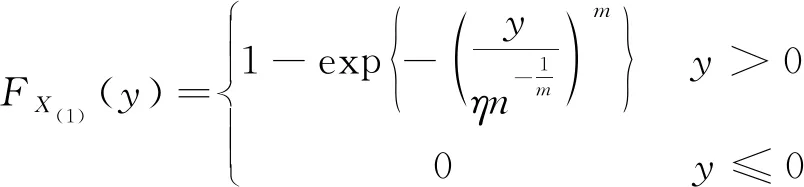
所以X(1)的密度函数表示为
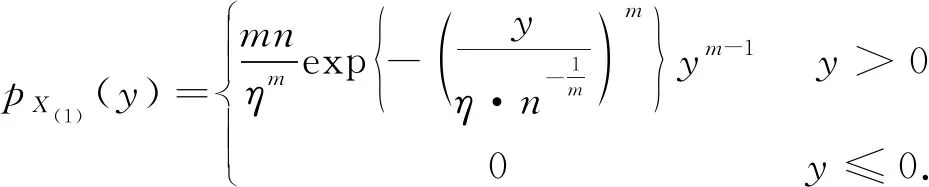
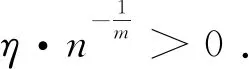
引理2设总体分布为Weibull 分布,X1,X2, …,Xn为其样本, 设X(1)和X(n)分别是样本的最小和最大次序统计量, 则(X(1),X(n)) 的联合密度函数表示为
ym-1zm-1.
证明
令 (X(1)X(n))(Y,Z),
当y≤z时,
F(X(1), X(n))(y,z) =Pr(Y≤y,Z≤z)
=Pr(Z≤z)-Pr(Y>y,Z≤z)
=Pr(X1≤z)…Pr(Xn≤z)-Pr(y Pr(y 当y>z时,F(X(1), X(n))(y,z)=0 即(X(1),X(n))的联合分布函数表示为 所以y≤z时, (X(1),X(n))的联合密度函数表示为 定理1设X1,X2, …,Xn是来自Weibull分布的一个样本, 又设X(1)和X(n)分别是从Weibull分布抽取样本的最小和最大次序统计量, 则样本极差W=X(n)-X(1)和样本中程(中位数) 证明 所以由变量变换法[8]和引理2, 可以得到(W,Q)的联合密度函数表示为 定理2设随机变量X1,X2, …,Xn服从双参数Weibull分布, 又设X(1)和X(n)分别是从Weibull分布抽取样本的最小和最大次序统计量, 则 (1)X(1)的k阶原点矩表示为 (2)X(n)的k阶原点矩表示为 (3)X(1)X(n)的k阶原点矩表示为 证明 (1)令X(1)Y, 由引理1可以得到 (2)令X(n)Z, 由引理1可以得到 即X(n)的k阶原点矩表示为 (3)由引理2可以得到 ym-1zm-1ykzkdz 所以 再由不完全伽玛函数[9-10]的计算公式可以得到 所以 假设X1,X2,…,Xn是对某产品进行寿命试验抽取样本容量为n的一个样本,X(n)和X(1)是样本的最大最小次序统计量,W=X(n)-X(1)是样本极差, 在描述样本变化幅度以及离散程度上, 样本极差受异常值影响较小, 广泛应用于各类试验的研究分析, 并在研究过程中样本极差的期望和方差是必不可少的. 下面对随机变量X如果服从Weibull分布, 求解出样本极差W=X(n)-X(1)的期望和方差表达式, 具体如下所述: 该表达式有两种求解方法, 第一种是利用定理1中已有的样本极差和样本中程的联合密度函数, 代入边际密度公式 p(w=X(n)-X(1))(w) 再代入期望和方差求解公式得到样本极差的期望和方差; 第二种是利用定理2中已有的X(1)的k阶原点矩和X(n)的k阶原点矩, 令k等于1和2求得样本极差的期望和方差. 下面用更简便的第二种方法进行求解。 本文在Weibull型分布下, 详细地推导和计算了最大和最小次序统计量的密度函数, 联合密度函数, 高阶原点矩, 有明确的表达式, 并应用到样本极差的期望和方差的计算中, 对理解和运用Weibull分布的最大和最小次序统计量矩计算有一定的借鉴意义。
2 定理
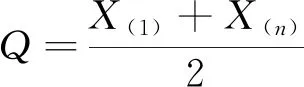


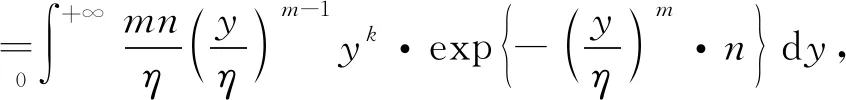


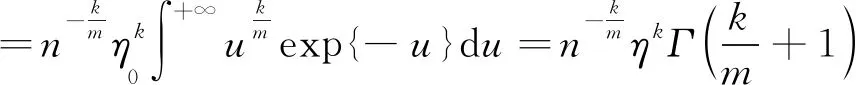

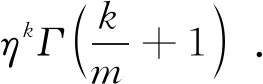
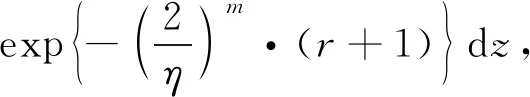


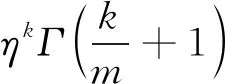

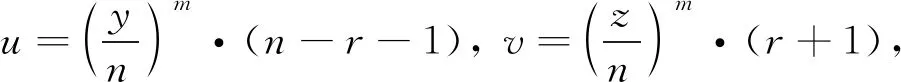

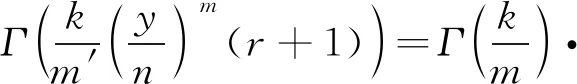
3 应用

4 结语
