一元多项式因式分解的一种方法
2022-04-13高来志
高来志
(洛阳市环境保护设计研究所, 河南 洛阳 471000)
判别一元多项式环P[x]中的一元多项式f(x)在不做开方运算条件下是否可分解, 把可分解的一元多项式分解成f(x)=g1(x)r1g2(x)r2…gl(x)rl, 目前还没有一般的有效方法[1-2]. 解决这个问题对彻底解决非线性代数方程(组)难题有重要意义. 笔者以文献[3]的消元方法为基础提出了一元多项式因式分解的一种方法.
1 构造b1,b2,…,bm的导出结式和导出多项式簇
设
f(x)=a0xn+a1xn-1+…+an(n≥3)
(1.1)
为数域P中任意给定的一个一元本原整系数多项式或一元整式实系数(复系数)多项式(f(x)的系数和常数项中没有公因子、不含分母、有理数和根式内的有理数为整数).
设
g0(x)=xm+b1xm-1+…+bm(2≤m (1.2) 为f(x)的因式. 建立f(x),g0(x)的西尔维斯特结式矩阵:[2] (1.3) 对结式矩阵(1.3)进行n步消元, 把其化成阶梯形矩阵 (1.4) 其中 i,j=n+1,n+2, …,n+m (1.5) 在m2个hij(b1,b2, …,bm)多项式中, 挑选项数少、bt(1≤t≤m)最高次幂低和个数少的m个多项式为hs(b1,b2, …,bm)多项式. 在m个hs(b1,b2, …,bm)多项式中, 择其中一个bm最高次幂最低、项数最少的多项式为hmin(bm)多项式, 剩余的m-1个多项式为hs1(bm)多项式. 由此构造b1,b2, …,bm的导出结式和导出多项式簇: res (hs1,hmin,bm)=βs1hs1(b1, …,bm-1) s1=1, …,m-1 res (hs2,hmin,bm-1)=βs2hs2(b1, …,bm-2) s2=1, …,m-2 …… res (hsm-1,hmin,b2)=βsm-1hsm-1(b1) sm-1=1 (1.6) 1) 仿照求有理根的方法, 对f(x)的首项系数和常数项做因子分解, 用f(x)的首项系数因子和常数项因子试算, 找f(x)的根. 若找到f(x)的根, 分解f(x)的一次因式. 否则f(x)中没有可分解的一次因式. 2) 对f(x)分解一次因式后, 若剩余部分是一个四次或四次以上多项式, 视这个多项式为f(x). 用上节的方法构造b1,b2, …,bm的导出结式和导出多项式簇. 仿照求有理根的方法, 对hsm-1(b1)多项式的首项系数和常数项作因子分解, 用hsm-1(b1)的首项系数因子和常数项因子试算, 找hsm-1(b1)的根. 把找出的hsm-1(b1)的根b1代入res (hsm-1,hmin,b2) 结式的三角形结式的倒数第2行, 求出b2;把b1、b2代入一个res (hsm-2,hmin,b3)结式的三角形结式的倒数第2行, 求出b3;…… ;把b1,b2, …,bm-1代入一个res (hs1,hmin,bm)结式的三角形结式的倒数第2行, 求出bm. 在g0(x)上乘一个适当整数或一个适当整式, 使其变成一元本原整系数或一元整式实系数(复系数)因式g(x)(g(x)的系数和常数项中没有公因子、不含分母、有理数和根式内的有理数为整数). 分解f(x)的因式g(x). 否则, 找求不出b1,b2, …,bm,f(x)中没有可分解的g0(x)因式. 按这种方法, 依次分解f(x)的二次和二次以上因式, 直至f(x)的可分解因式被完全分解为止. 3) 最后, 根据分解结果, 写出f(x)的分解式. 4) 如果f(x)的首项系数或常数项、hsm-1(b1)的首项系数或常数项是由多种数混合组成的多项数构成, 用如下方法进行因子分解:找出项与项中有公因子的所有组合, 把每个组合的所有项合并和把公因子提到括号外边, 把括号中内容相同的不同组合合并, 得分解的每个因子. 否则, 所给首项系数或常数项不能分解. 5) 根指数相同的根式与根式做乘除, 只许根式内的根底数与根底数做乘除, 不可化简. 证明 矩阵(1.3)是根据矩阵的线性相关定义建立起来的, 因为g0(x)是f(x)在不做开方运算条件下或做开方运算条件下的可分解因式, 对矩阵(1.3)进行n-1步消元后, 第n行的非零元素和第n+i行(1≤i≤m)的非零元素成比例, 所以,n步消元结果(1.5)式成立. (1.6)式是根据两个不同多项式有公根结式为零的定理构造出来的[2].f(x)在不做开方运算条件下存在可分解因式g0(x)时,b1,b2, …,bm直接存在于矩阵(1.3)、 矩阵(1.4)、 (1.5) 式、 (1.6) 式中, 利用(1.6)式可找求出b1,b2, …,bm;f(x)在不做开方运算条件下不可分解时,b1,b2, …,bm不存在, 从(1.6) 式中找求不出b1,b2, …,bm. (1) 最后, 得f(x)的分解式为 f(x)=3x4-8x3-4x2-2x+15 解:设g0(x)=x3+b1x2+b2x+b3是f(x) 的因式. (1) (2) (3) 解:第1步, 找出项与项中有公因子的所有组合, 把每个组合的所有项合并和把公因子提到括号外边. 第2步, 把括号中内容相同的不同组合合并, 得分解的每个因子. 第3步, 综合以上分解结果, 得多项数的因子分解式. 本文提出的一元多项式因式分解方法, 从理论上和实际上完全解决了一元有理系数多项式有理分解的判别和分解问题, 同时, 也解决了一元实系数多项式和一元复系数多项式在不做开方运算条件下因式分解的判别和分解问题.
2 一元多项式因式分解的具体方法
3 算例
3.1 试分解因式
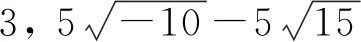
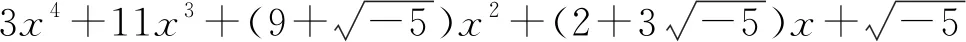
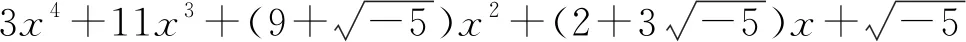
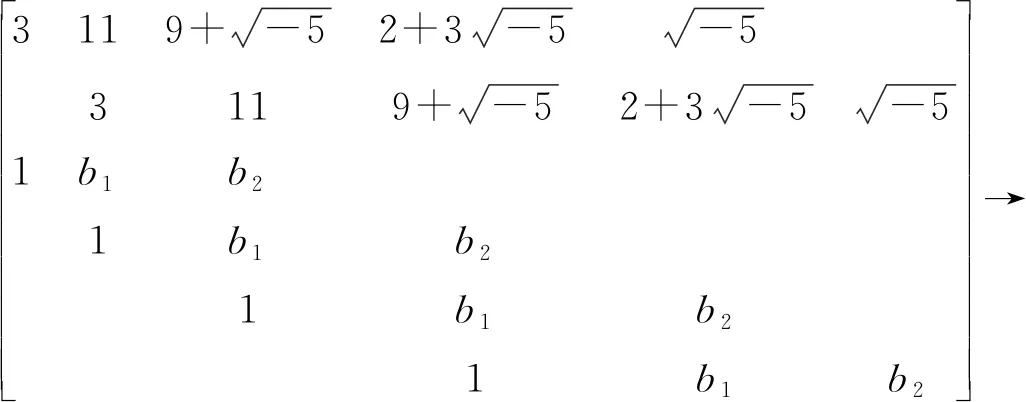

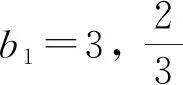
3.2 试分解三次因式
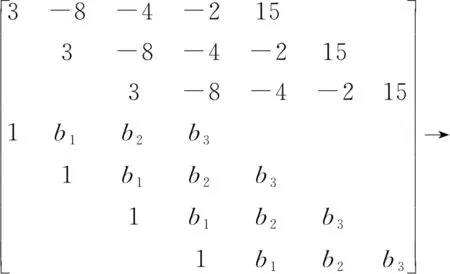
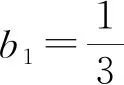
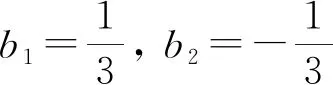
3.3 试对多项数作因子分解
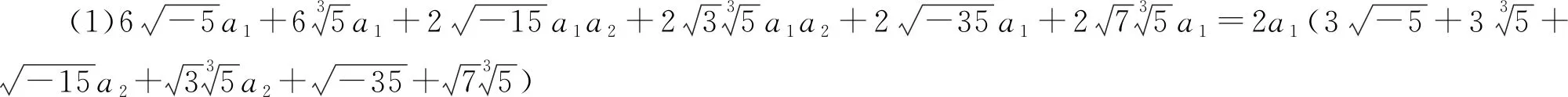
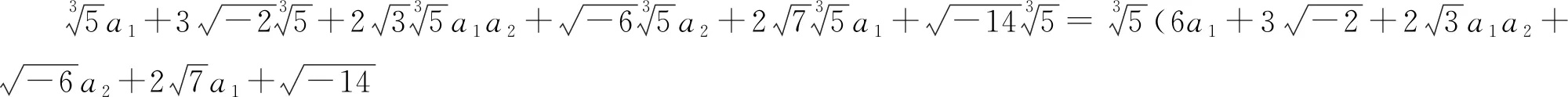
4 结论
