涉及导数应用的创新题赏析

龙大维

(云南省德宏州民族第一中学，678400)

导数是初等数学与高等数学的重要衔接点,是研究函数的单调性、极值、最值的重要工具.由于当今高考命题注重“创新意识”的考查,涉及导数应用的问题更显创新思维的活力.本文列举此类问题中的几类创新问题,供大家赏析研究.

一、新定义创新题

例1定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“躺平点”.若函数f(x)=lnx,g(x)=x3-1的“躺平点”分别为α,β,则α，β的大小关系为( )

(A)α≥β(B)α>β

(C)α≤β(D)α<β

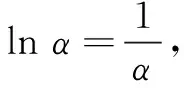
又α<β时，α≤β也成立.故选C，D.

评注本题借助函数“躺平点”的新定义,使导数的计算与方程思想、逻辑推理融为一体,用新定义迁移信息,形式新颖别致,有效考查了学生的迁移创新能力.

二、问题研究创新题

例2(2021年清华大学中学生标准学术能力(THUSSAT)诊断性测试题)有同学在研究指数函数y=2x和幂函数y=x2的图象时,发现它们在第一象限有两个交点(2，4)和(4，16).通过进一步研究,该同学提出了如下两个猜想:

(1)函数y=ex与函数y=xe的图象在第一象限有且只有一个公共点;

(2)设a>1,b>1,且a≠b，若ab>ba,则ab>e2(其中e为自然对数的底).

请你证明或反驳该同学的猜想.

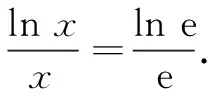
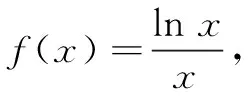
综上,方程ex=xe有唯一的实根e，猜想(1)正确.

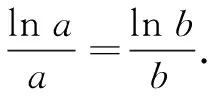
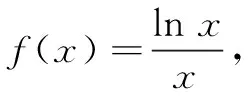
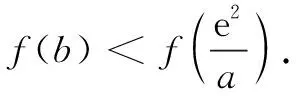
评注本题在研究函数y=2x和y=x2图象的交点个数的基础上，提出两个猜想，使问题的设问背景创新，在新颖的形式下很好地考查了导数知识的应用.本题要求学生根据问题新情境构设新函数，利用导数研究函数的单调性等知识进行推理论证，对猜想作出判断.

三、方法应用创新题

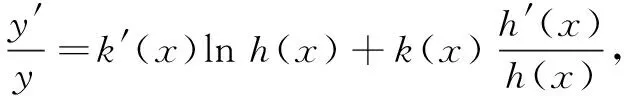
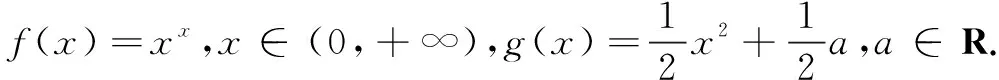
(1)求y=f(x)在x=1处的切线方程；

(2)若∀x∈(0,+∞)，f(x)≥g(x)恒成立，求a的取值范围.

解(1)由y=f(x)=xx,不妨设函数h(x)=x,k(x)=x,则由幂指函数导数公式，可得f′(x)=xx(lnx+1),所以f′(1)=1.

又f(1)=1,故所求切线方程为y-1=x-1,即y=x.

(2)先寻找必要条件：依题意，有f(1)≥g(1)，解得a≤1.下面证明其充分性：当a≤1时，f(x)≥g(x)在(0,+∞)恒成立.

令M(x)=F′(x),则M′(x)=xx(lnx+1)2+xx-1-1=exln x(lnx+1)2+e(x-1)ln x-1.由x-1与lnx同号，得(x-1)lnx≥0，从而e(x-1)ln x≥1.又exln x(lnx+1)2≥0，所以M′(x)≥0，M(x)即F′(x)在(0,+∞)单调增.

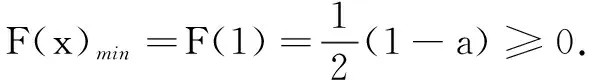
综上，得a的取值范围为(-∞,1].

评注本题首先给出幂指函数定义及求导方法,要求学生在理解新定义和求导方法的基础上,运用导数研究含幂指函数的新函数的相关问题.第(2)问先寻找不等式恒成立的必要条件,然后证明充分性成立,这一新的具体思路值得学生认真体会.