基于磁路模型的新型半包围磁芯结构设计及优化
2022-04-11谢哲慧夏能弘
谢哲慧,夏能弘
(上海电力大学电气工程学院,上海 200090)
无线电能传输是通过高频磁场将电能经气隙耦合到负载端,实现无物理接触的能量传递过程,该充电方式具有恶劣环境适应性、便于维护、安全可靠等优点,被广泛应用于各种充电场合[1-6]。然而无线电能传输系统的原副线圈之间距离较大,且在传能过程中存在大量的磁场泄漏,会造成系统耦合系数下降,因此,将系统耦合系数作为衡量无线充电系统传能性能的设计指标。
无线电能传输系统的核心部分是松耦合变压器,其优劣直接影响系统磁场的耦合和空间电磁辐射[7]。本文以一种用于机器人无线充电系统的小尺寸平面圆形线圈结构为对象进行研究,通过设计松耦合变压器的磁芯结构来提高系统传能性能。文献[8-10]提出设计不同形状的磁芯结构来增强系统的耦合性能,如铁氧体板、EE型磁芯、U型磁芯等;文献[11]分析带屏蔽结构的磁芯可增强系统传输功率,尤其是在传输距离较远的情况下;文献[12]中提出了一种应用于螺旋形发射线圈的圆柱形磁芯,但采用大量的磁芯会额外增加机器人自身负重和机械损耗,不适用于机器人无线充电系统。
本文提出了一种新型半包围磁芯结构,基于对圆盘磁芯的磁路模型以及耦合系数的磁路表达式分析,得到可以通过减小互耦区磁阻和增大自耦区磁阻来设计磁芯结构。依据系统耦合系数和线圈下方径向位置的磁通密度作为设计指标,结合Ansys Maxwel有限元仿真分析,得到最优磁芯结构参数,提高系统传能性能且减小电磁辐射对系统的影响。
1 新型半包围磁芯结构设计
1.1 等效磁路模型
1.1.1 圆盘磁芯磁路模型
由于磁芯的磁导率远大于空气的磁导率,一般在磁路分析中忽略磁芯中的磁阻,仅考虑在空气中的磁通路径,圆形线圈模型如图1所示。对图1(a)圆盘磁芯的无线充电系统进行有限元分析,经仿真结果发现,其磁场基本是对称分布的,因此可近似用YOZ面磁通分布特征进行分析。
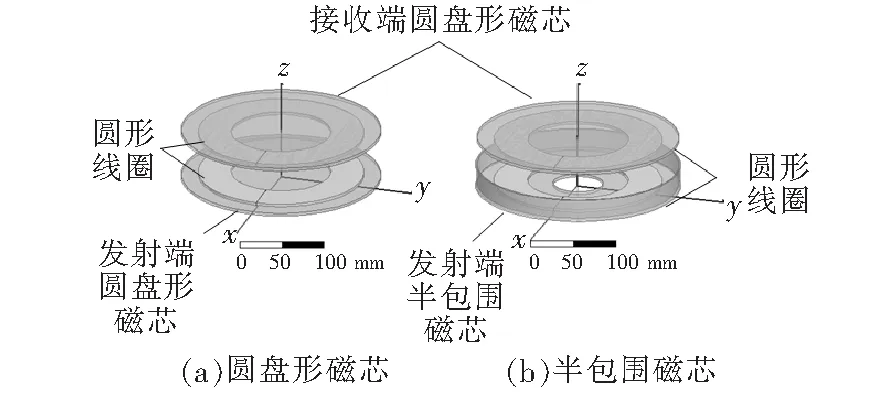
图1 圆形线圈模型Figure 1 Model of circle coil coupler
结合图2所示的圆盘磁芯磁通分布,将磁通分为互耦区与自耦区2部分[13]。互耦区为m1、m2区,磁通由原边电流产生,同时匝链副边绕组。自耦合区为L区,磁通由原边电流产生的,但未匝链副边绕组。

图2 圆盘磁芯磁通分布Figure 2 Magnetic flux distribution of disc core
令互耦合m1、m2区对应的磁阻为Rm1、Rm2,自耦合L区对应的磁阻为RL,磁动势为F,其等效磁路模型如图3所示,可推导出耦合系数的磁路表达式为
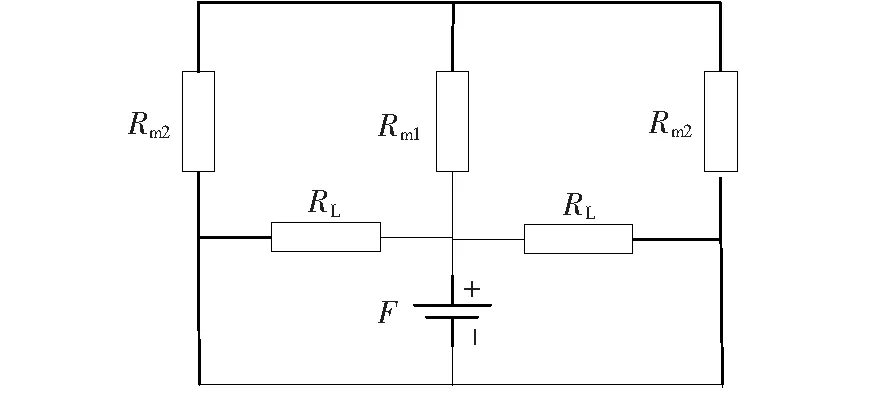
图3 等效磁路模型Figure 3 Equivalent magnetic circuit model
k=
(1)
由式(1)可知,系统耦合系数与自耦、互耦区的磁阻有关,要增大系统耦合系数,可以通过减小Rm1、Rm2和增大RL来实现。
1.1.2 半包围磁芯磁路模型
基于对圆盘磁芯的磁路模型分析,在原副线圈之间的传输距离固定的情况下,适当减小互耦区磁阻和增大自耦区磁阻可以作为设计磁芯结构的依据。其中,磁阻表达式R=l/μA,l为磁路长度,A为磁路截面积,μ为介质磁导率。由此可知,磁阻主要取决于磁路的几何尺寸和介质的磁导率。减小互耦区磁阻Rm2,可以通过减小原副边磁芯边沿之间的空气磁路长度来实现;增大自耦区磁阻RL,可以通过减小磁通经过发射端磁芯的磁路长度来实现,提出如图1(b)所示的新型半包围磁芯结构。
半包围磁芯模型相比圆盘磁芯模型,在发射端磁芯的外沿增加磁环,即m2区可以等效认为磁路中减小了一个与磁环相同几何尺寸的空气介质磁阻ΔRm2,此时m2区磁阻记为R′m2;发射端中心挖空半径为r的磁芯,即L区可以等效认为磁路增加了一个与挖去圆盘相同几何尺寸的空气介质磁阻Ra,此时L区磁阻记为R′L,其等效磁路模型如图4所示。

图4 半包围磁芯磁路模型Figure 4 Magnetic circuit model of semi-enclosed core structure
其中,R′L的磁阻表达式为
(2)
R′m2的磁阻表达式为
(3)
式中r为发射端磁芯内环半径;R为圆盘磁芯半径;h为半包围磁芯磁环壁高度;d为半包围磁芯磁环壁厚度。结合式(2)、(3)可得到系统耦合系数的磁路表达式为
(4)
由式(4)可知,系统耦合系数与磁芯内环半径r、半包围磁芯磁环壁高度h和半包围磁芯磁环壁厚度d有关。
1.2 等效电路模型
针对提出的新型半包围磁芯,采用SS补偿作为该无线电能传输系统的补偿拓扑结构,等效电路如图5所示,其中,US为高频交变电源,RL为负载电阻,Rp、Rs为原副线圈的等效电阻,LP、LS为原副线圈的等效电感,CP、CS为原副线圈的补偿电容,M为原副线圈之间的互感,I1、I2为流经原副线圈电流。
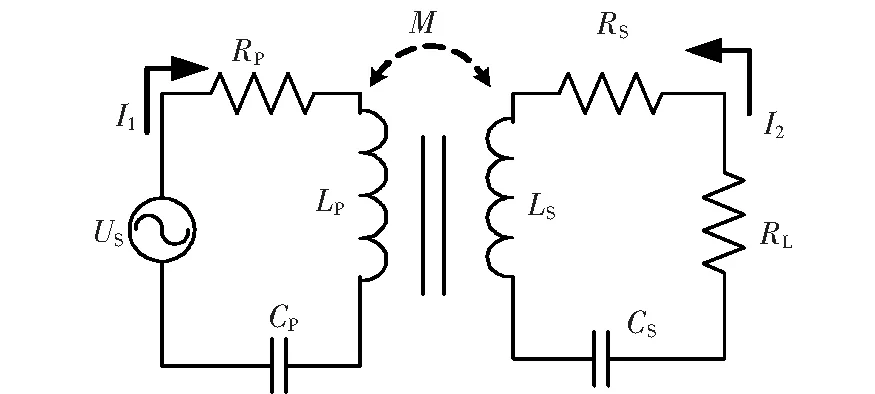
图5 等效电路模型Figure 5 Equivalent circuit model
根据KVL定律得:
(5)
则输出功率表达式为
(6)

(7)
输入功率表达式为
(8)
电感LP、LS的品质因数分别为
(9)
(10)
可推导出系统的传输效率表达式为
(11)
综上分析,得到相关结论:一次侧电流一定的情况下,系统输出功率与耦合系数有关,耦合系数越大,输出功率越大;在负载RL一定的情况下,系统效率与耦合系数k、线圈内阻和品质因数有关,对于特定的无线充电系统,线圈电阻和品质因数可看作常数[14],那么系统的传输效率仅与耦合系数相关。
2 半包围磁芯结构系统特性分析
半包围磁芯结构特征主要表现在圆盘磁芯中心挖空和增加磁环壁,其中,磁芯中心挖空是为了增大自耦区磁阻,而增加磁环壁的作用是减小互耦区的磁阻。考虑到磁路模型中互耦区包括磁芯中间部分和磁芯外径部分,磁环的位置会影响系统的传输性能。其中,系统的耦合性能和对系统周围空气的电磁辐射是衡量无线充电系统传输性能的重要因素,由于发射端主要埋于地下,本文仅考虑对发射端电路板的影响,选取发射线圈下方10 mm处径向磁通密度变化量来反映电磁辐射程度。
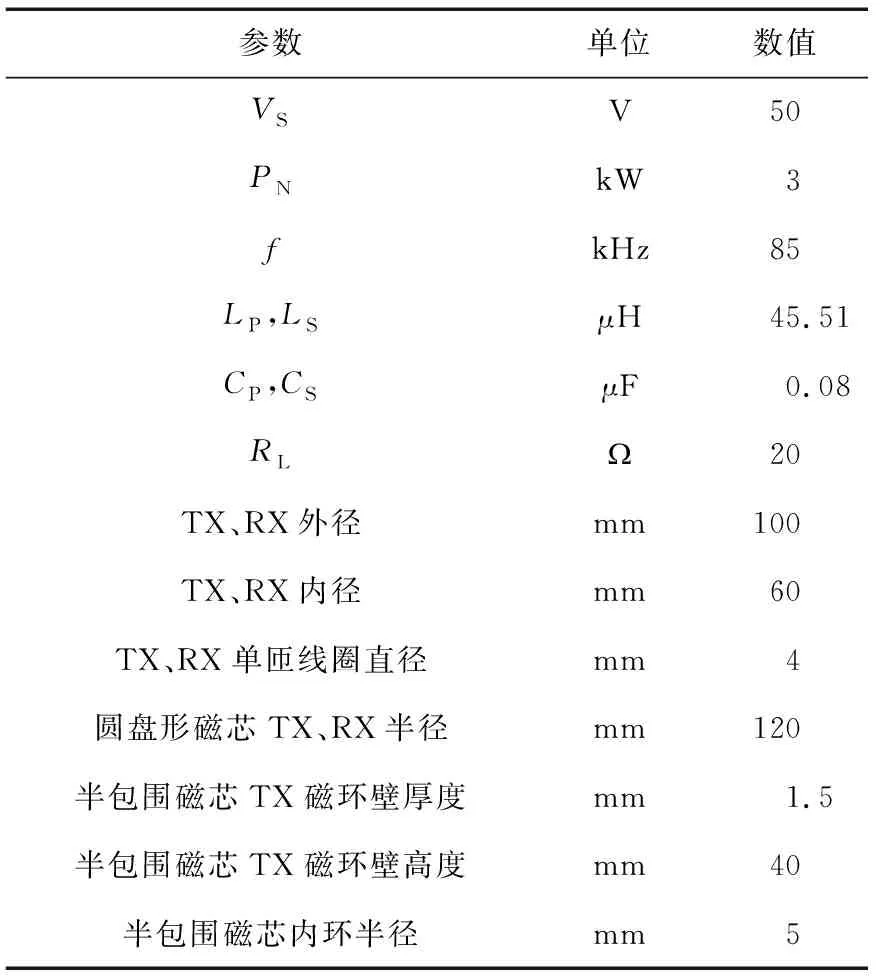
利用Ansys Maxwell分别建立了不加磁环壁的圆盘磁芯、只加内磁环壁的圆盘磁芯、只加外磁环壁的圆盘磁芯以及内外都加磁环壁的圆盘磁芯模型,仿真模型参数如表1所示,其中TX为发射线圈,RX为接收线圈。
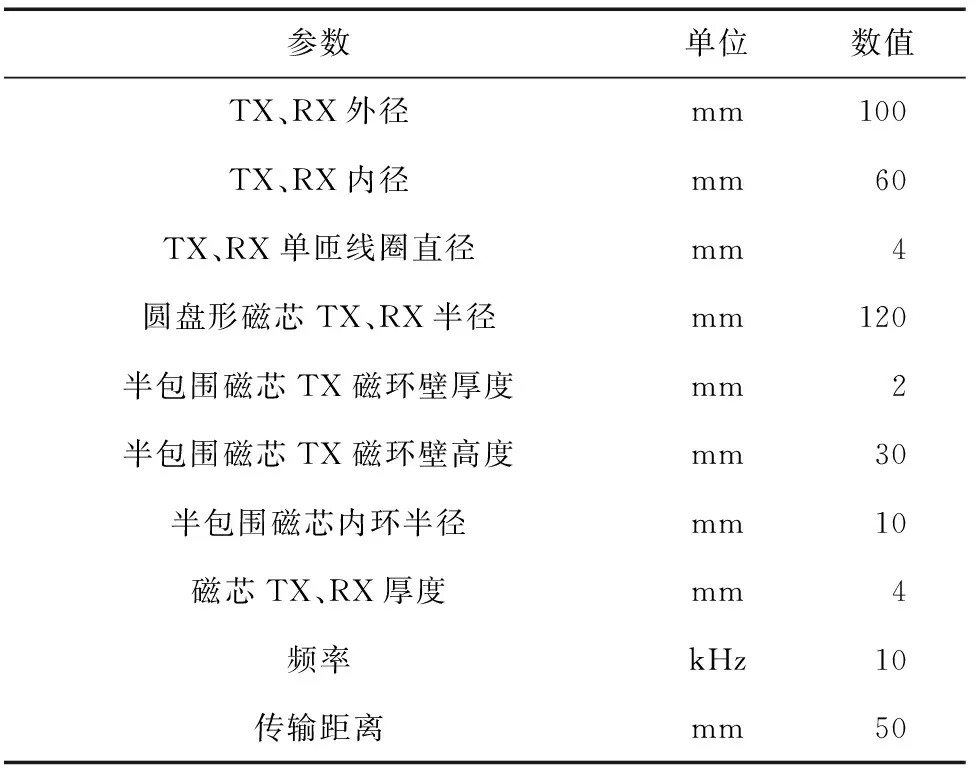
表1 仿真模型参数Table 1 Parameters of the simulation model
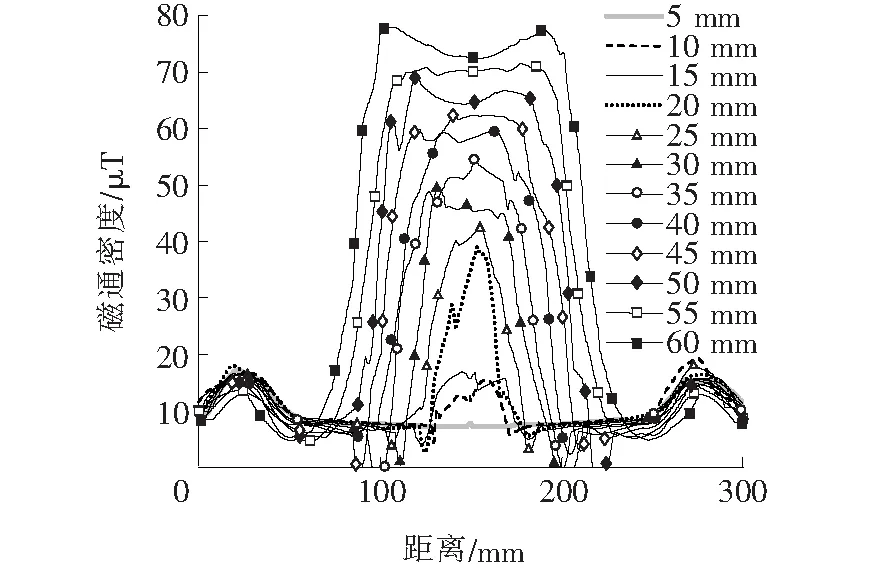
仿真结果如表2所示,在4种情况下,增加磁环壁比不加磁环壁的耦合性能提高了3.4%以上,不同位置添加磁环壁的仿真模型的耦合系数基本相同。与不加磁环壁的系统相比,只加外磁环壁的系统屏蔽效果提升了64.1%,只加内磁环壁的系统屏蔽效果提升了5.1% ,既加外磁环壁又加内磁环壁的系统屏蔽效果提升了60.2%。并且由图6所示的发射线圈下10 mm处径向磁通密度可知,采用加外磁环壁的磁芯结构时,能将磁场有效地约束在传能区域,减少磁场的泄露,增强传能区域的磁场耦合。综上所述,只需要添加外磁环壁既可提高系统内部的耦合性能,又可降低系统对外的电磁辐射。

图6 发射线圈下10 mm处径向磁通密度Figure 6 Radial magnetic flux density at 10 mm under transformer coil

表2 仿真结果Table 2 Simulation result
综上,新型半包围磁芯结构在耦合性能和电磁辐射方面较圆盘磁芯结构都有一定提升,说明该磁芯结构有可行性,下文具体分析新型半包围磁芯结构参数(磁环壁厚度d、磁环壁高度h和磁芯内环半径r)对系统耦合系数和电磁辐射的影响,分析不同磁芯结构参数下的系统特性,在分析时仅改变需要分析的结构参数,其余仿真模型参数如表1所示。
2.1 磁环壁厚度
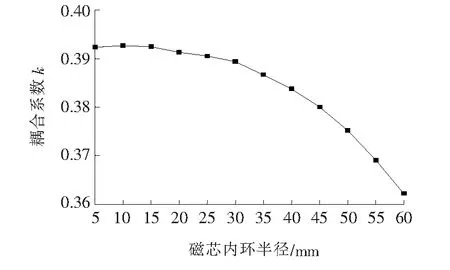
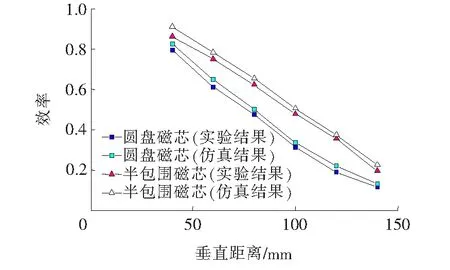
为分析不同磁环壁厚度(mm)(1 图7 半包围磁芯环厚度对系统耦合系数影响Figure 7 Influence of semi-enclosed core thickness on coupling coefficient 图8 不同磁环壁厚度对应的发射线圈下10mm处径向磁通密度Figure 8 Radial flux density at 10mm under transformer coil corresponding with different thickness 为分析不同磁环壁高度(mm)(10 图9 半包围磁芯环高度对系统耦合系数影响Figure 9 Influence of semi-enclosed core height on coupling coefficient 图10 不同磁环壁高度对应的发射线圈下10 mm处径向磁通密度Figure 10 Radial magnetic flux density at 10 mm under transformer coil corresponding to different height 圆盘磁芯中间和外边缘的磁通密度较低,磁芯利用率不高,所以采用中心挖空的磁芯结构,但考虑到线圈周围的磁通密度较高,故磁芯的内环半径必须小于线圈的内径,以减小线圈周围的磁场泄露。为分析不同磁芯内环半径(mm)(5 图11 半包围磁芯内环半径对系统耦合系数影响Figure 11 Influence of semi-enclosed core inner radius on coupling coefficient 由图11可知,系统耦合系数随着磁芯内环半径的增大而变小,且当磁芯内环半径大于30 mm时,耦合系数急剧下降;由图12可知,磁芯内环半径小于15 mm时,电磁辐射较小,随磁芯内环半径的增大,电磁辐射越强,造成该现象的原因在于适当增大磁芯内环半径,即增大以磁芯内环半径构成的介质为空气的圆盘处磁阻,可以有效地抑制系统耦合系数的下降,但是随着磁芯内环半径增大,线圈内径侧磁场会大量泄漏到空气中,导致系统耦合系数下降以及电磁辐射加剧。因此,可将磁芯内环半径作为影响系统特性的设计参数。 图12 不同磁芯内环半径对应的发射线圈下10 mm处径向磁通密度Figure 12 Radial magnetic flux density at 10 mm under transformer coil corresponding to different core inner radius 考虑系统耦合系数和电磁辐射2个关键因素,对磁环壁高度h及磁芯内环半径r进行优化。h和r均存在上下限且系统设计应尽可能减少磁芯的用量以降低成本,因此优化目标函数定义为 (11) 式中h为磁环高度;r为磁芯内环半径;hmin、hmax分别为h的最小值和最大值;rmin、rmax分别为r的最小值和最大值;k为半包围磁芯的耦合系数;kN为圆盘磁芯的耦合系数;B为半包围磁芯发射端线圈下10 mm处径向磁通密度;BN为圆盘磁芯发射端线圈下10 mm处径向磁通密度;α1、α2、α3、α4均为设定的权重系数。 通过Maxwell仿真计算得到(h,r)的目标函数值,但仿真计算时间较长。本文采用贝叶斯优化算法(bayesian optimization algorithm,BOA)对仿真模型进行优化,以得到最优(h,r)函数值。BOA是一种在目标函数未知的情况下根据已有采样点(仿真结果)求取函数最大值的有效算法,根据需求决定采样数据,不同(h,r)下的耦合系数和磁场强度均可由仿真软件计算得到,仿真结果运用于Python3环境下的优化模型,计算出目标函数。若2次目标函数值和优化变量的差分别小于0.01和0.001,则优化过程结束。否则,根据提取函数(acquisition function,AF)选择的新采样点,更新优化变量,重复之前的过程,同时更新高斯过程及提取函数。经BOA优化可得最优参数结果:磁环壁高度h为35 mm;磁芯内环半径r为15 mm。此时,新型半包围磁芯的系统耦合系数为0.392,较圆盘磁芯系统耦合系数提高了5.1%。新型半包围磁芯最大磁通密度为16.930 μT,较圆盘磁芯的系统屏蔽效果提升了1.46倍。 为了验证仿真的正确性和新型半包围磁芯结构的合理性,搭建如图13所示的实验平台。当系统谐振频率设为85 kHz、输入电压取330 V、载流密度约为4 A时,系统的铜损及线材使用率达到较好的平衡,考虑到线圈工作的电流密度,选用19股AWG-38 litz线(截面积6.28 mm2)。实验结果由矢量网络分析仪E5061B(带选件006)测量。 图13 实验平台实物Figure 13 Experimental setup 考虑到铁氧体磁芯定制模具的价格较高,实验采用几何尺寸为43 mm×10 mm×1.5 mm的铁氧体拼接而成,误差小于2%。分别将发射端为圆盘磁芯和半包围磁芯结构接入搭建的实验平台中,测不同气隙距离下系统的传输效率,实验几何参数和等效电路参数如表3所示。 表3 实验原型参数Table 3 Parameters of the experimental prototype 仿真系统与实验系统保持同参数,仿真结果由Ansys与Simplorer联合仿真得到,记录不同气隙距离下圆盘磁芯和半包围磁芯的系统传输效率变化曲线,结果如图14所示,由图14可知,新型半包围磁芯结构的传输效率优于圆盘形磁芯结构,说明半包围磁芯结构可以有效地提高传能区域的磁场耦合性能。 图14 系统效率对比Figure 14 Comparison in efficiency 本文基于磁路模型的分析,提出一种应用于机器人无线充电的小尺寸圆形线圈的新型半包围磁芯结构,得到以下结论。 1)适当减小互耦合区的磁阻和增大自耦合区的磁阻,可以有效地提高系统耦合性能,并作为磁芯设计的依据。 2)新型半包围磁芯的磁环壁高度和磁芯内环半径会影响系统的耦合性能和电磁辐射效果,而磁环壁厚度对系统特性影响不明显。 3)优化后的半包围磁芯结构较圆盘磁芯系统耦合系数提高了5.1%,线圈下方屏蔽效果提升了1.46倍。 因此,新型半包围磁芯结构具有合理性,能够有效地提高系统耦合性能,降低非传能区域的电磁辐射。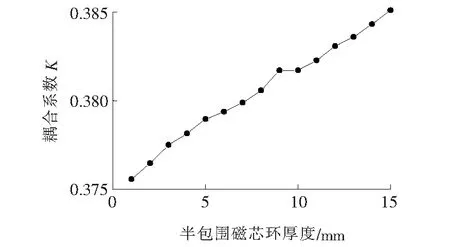

2.2 磁环壁高度
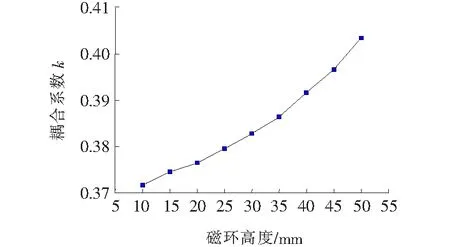
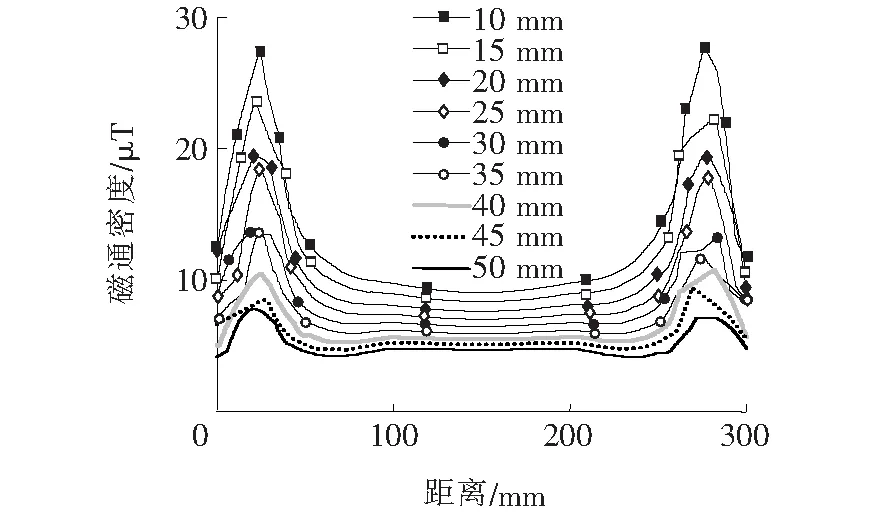
2.3 磁芯内环半径
3 半包围磁芯结构参数优化
4 实验验证

5 结语
