考虑置信水平的混合储能平抑风电波动

马 瑞，李 浩，吴震宇

(长沙理工大学电气与信息工程学院，湖南 长沙 410114)

自21世纪以来，能源问题已经成为世界性的难题。随着越来越多的新能源被发现，传统能源枯竭的问题有望得到解决，但是新能源发电由于其出力的间歇性和随机性，很难直接被电网利用，加入储能装置能有效地解决这一问题[1-2]。

目前，储能参与风电等新能源的消纳场景日益增多，其运行原理主要有差额补充、波动平抑分析和经济特性优化(即经济性评估)这3大类。文献[3]根据入网风电和储能系统时间与空间上的相关特性以及风火储联动协调，构建了考虑风储系统功率传递与能量时空多维度输移特性、储能系统能量周期性循环与功率能量转移守恒规律、风火储系统互动耦合特征影响并兼顾其功率调节与能量输移双重效用的容量多指标优化配置数学模型；文献[4]中的储能配置方法将储能运行的动作时机和动作深度作为边界条件；文献[5]通过讨论电池储能(battery energy storage system，BESS)参与电网一、二次调频的实现方法，提出了与火电机组具备同等调频能力的BESS优化配置方法；文献[6]提出了一种滑动平均与经验模态分解(empirical mode decomposition，EMD)共同参与的混合储能(hybrid energy storage system，HESS)功率和容量配置方法，并且考虑了全寿命周期成本(life cycle cost，LCC)以及风电场的经济效益，通过净效益最高寻求最优的储能配置；文献[7]提出了一种利用HESS缓解短期和长期波动的风电过滤方法，并通过基于小波变换方法进行混合储能的优化配置；文献[8]利用多场景随机规划与序贯蒙特卡洛模拟方法对风电场内储能系统优化配置，并考虑了储能寿命损耗。

以上文献在风电波动平抑周期内对风电波动率明显偏高的单一时刻也进行了相应储能配置，极大地浪费了储能设备投资。基于此，本文提出一种考虑置信水平的混合储能平抑风电波动新方法。首先对比在不同时间常数下混合储能对典型日风电出力波动的平抑效果，得到储能参考功率；然后采用EMD将储能参考功率分解成一系列本征模态函数(intrinsic mode function，IMF)，利用瞬时频率—时间曲线混叠最少将储能参考功率划分为功率型高频储能配置和能量型低频储能配置，基于储能成本对其进行合理选型；最后对湖南某地风电场实际数据进行算例仿真。仿真结果表明：考虑置信水平后，储能平抑风电波动所需要的容量和功率明显降低。

1 考虑风电波动率置信水平的出力平抑方法

本文通过低通滤波方法进行风电波动平抑，将风电出力的低频分量注入电网，其原理如图1所示。

图1 一阶低通滤波Figure 1 First-order low-pass filtering

并网功率为

(1)

式中τ为时间常数；Pf为风电的输出功率。

将式(1)离散化处理，一个模拟周期时长为Δt，当模拟时段为tk=kΔt时[12]，并网联络线第k时刻功率为

(2)

式中Pf(k)为风电第k时刻的输出功率；Pline(k-1)为并网联络线第k-1时刻功率。

由式(2)分析可知，当前时刻的并网功率受到通过前一时刻的并网功率和当前时刻的风电功率共同影响，但相邻时刻间的并网功率又存在一定相似之处，从而达到平滑并网功率，保障电能质量的作用。

传统风电波动率是风电出力曲线波动率全部小于设定值，而对于不同置信水平下风电波动率则以不同的概率小于功率波动率设定值。其中概率定义为

(3)

式中p为置信水平数值；Nx为平抑周期内波动率小于设定值的时段个数；N为平抑周期内的时段数。

2 考虑置信水平的储能功率配置方法

2.1 考虑置信水平的储能参考功率求取

风电出力的低频部分直接供给电网，高频部分由储能吸收或释放，则k时刻的储能补偿功率为

PE0(k)=Pf(k)-Pline(k)=

(4)

式(4)为储能功率求取方程，以储能放电功率为负，充电功率为正，不同置信水平下的功率求取是通过改变时间常数τ实现的，如何选取合适的τ成了关键。

2.2 混合储能系统功率分配

本文通过EMD分解储能功率需求，根据频率-时间曲线中相邻IMF的模态混叠最少进行分配[6]。将产生的高、低频信号分量分别作为功率型、能量型储能的参考功率，即

(5)

(6)

式中Ph为高频部分，作为功率型储能的参考部分；Pl为低频部分，作为能量型储能的参考部分；j为1～n的正整数。

2.3 储能周期电量平衡

由于本文是根据典型日为依据进行一天的储能配置，一个周期内储能的初始状态必须一致，所以在一天之内储能充电与放电电量之和必须为零，又由于储能电量E=P·T，即求一天之内功率之和为零。

(7)

P′E(k)=PE0(k)-ΔP

(8)

P′line(k)=Pline(k)+ΔP

(9)

式中 ΔP为储能功率平移量；P′E(k)为第k时刻储能修正功率；P′line(k)为第k时刻联络线修正功率。其中，k=1,2,…,N。

则储能修正功率为

P′EN=max[P′E(k)]

(10)

3 考虑风电波动率置信水平的储能容量配置方法

3.1 充放电量计算

由风电波动率不同置信水平下的参考功率求取储能的充放电电量，即

E[k]=

(11)

式(11)中除以3 600是将时间换算成小时，从而使得到的电量单位为kW·h。

3.2 额定容量计算

储能系统剩余的能量不断变化，一般通过系统的荷电状态来表示系统剩余能量水平，荷电状态(state of charge，SOC)计算方法为

(12)

式中S为储能系统实时荷电状态；S0为储能系统初始荷电状态；EN为储能系统额定容量。充电时，系统增加能量，E[n]为正，剩余能量增多，SOC增大；放电时，系统能量减少，E[n]为负，剩余能量减小，SOC降低。

设储能系统荷电状态最大和最小允许值分别为Smax和Smin，则

(13)

(14)

取满足以上条件的最小EN，求得：

(15)

(16)

求解可得：

(17)

3.3 初始状态确定

通过将式(13)、(14)中右侧相等，即可求得初始荷电状态为

(18)

通过储能参考功率值能够将储能能量变化的正向最大值与负向最大值求出，从而确定储能系统SOC的边界范围，通过SOC的边界范围能够得到储能的最小额定容量，进而求得储能初始状态。将储能系统调整在该初值状态，即可满足整个周期内的储能系统充放电需求。

4 混合储能选型模型

本文利用费用现值法，假定储能系统总寿命期为Yra，基准折现率为I，储能元件更新置换次数为n，建立储能的全寿命周期成本模型。

1)初始投资成本。

(19)

式中Cps为单位储能功率成本；Ces为单位储能容量成本。

2)更新替换成本。

C2=

(20)

式中Crep(k)为储能更新替换单位功率成本；Cree(k)为储能更新替换单位容量成本。

3)辅助设备成本。

(21)

式中Cbop为储能单位功率的辅助设备成本；Cboe为储能单位功率的辅助设备成本。

4)运行维护成本。

(22)

式中Comp为单位储能功率运行维护成本；Come为单位储能功率运行维护成本。

5)设备回收价值。

(23)

式中α为回收利益系数，在3%～5%之间。

综上，全寿命周期成本为

CLCC=C1+C2+C3+C4-C5

(24)

5 算例分析

仿真使用的数据为湖南某风电场数据，A风电场工程建设规模为50 MW，安装25台单机容量为2 MW的风电机组，取2016年某日96点风电出力数据进行分析，本文规定波动率平抑标准为30 min波动率低于10%，未平抑之前最大波动率达到了59%。低通滤波的关键是寻找到合适的时间常数τ，本文通过对典型日风电出力进行傅立叶频谱分析来寻找最优时间常数τ，所得典型日频谱曲线如图2所示。由图2可知，A风电场典型日风电出力的频率变化主要集中在1.16×10-5～5.67×10-4。

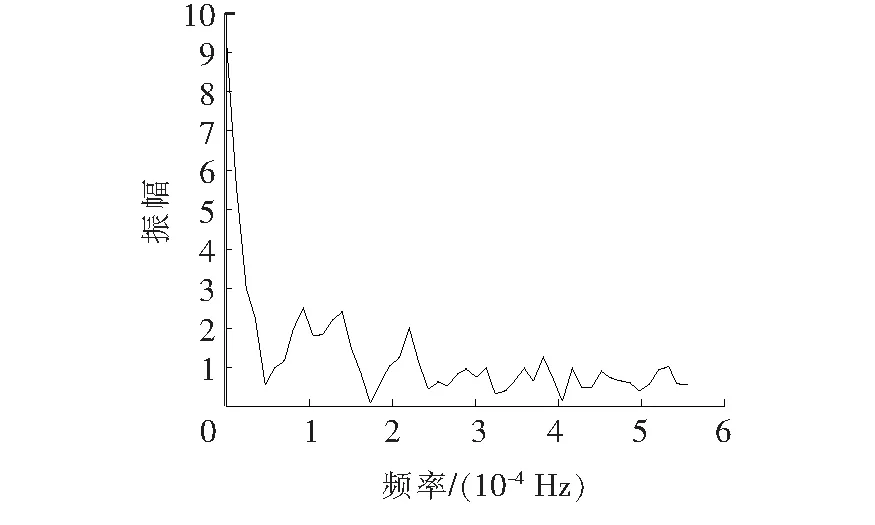
图2 A风电场典型日风电出力频谱Figure 2 A wind farm typical wind power output spectrum

根据风电场典型日出力频谱，从低频到高频依次选取几组时间常数，不同时间常数下风电出力平抑效果相差明显，如图3所示。由图3可知，当截止频率为1/39 000 Hz时，风电波动率达到规定要求。图3中不同截止频率下的波动率如表1所示。由表1可知，当时间常数为103.45 min时，波动率才能够满足要求，此时由程序求得储能修正后的参考功率为26.65 MW，其EMD分解波形如图4所示。

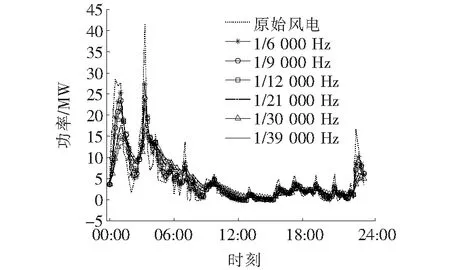
图3 不同截止频率下的入网功率Figure 3 Different cut-off frequencies into the network power

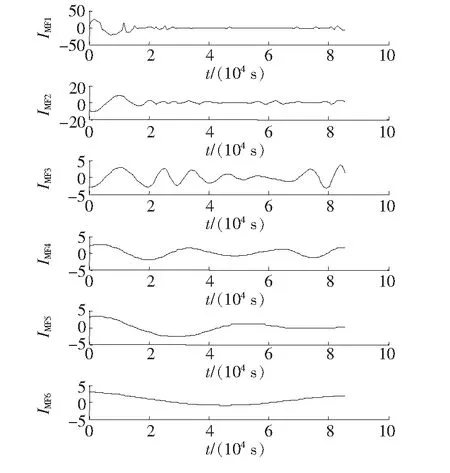
图4 全部IMF曲线Figure 4 All IMF curves

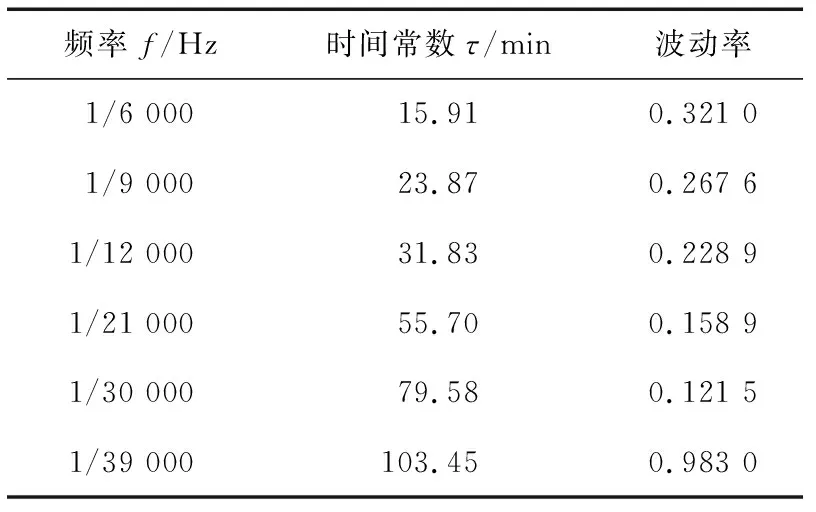
表1 不同截止频率下的波动率Table 1 Time constants and volatility at different cut-off frequencies

IMF瞬时频率—时间曲线如图5所示，由图5可知，IMF3与IMF4几乎没有重合部分，因此将IMF1到IMF3分为高频部分功率型储能参考功率，IMF4到IMF6为低频部分能量型储能参考功率。

图5 IMF瞬时频率—时间曲线Figure 5 IMF instantaneous frequency-time curve

从以上分析中难以分辨哪一种储能配置更加合理，因此本文提出了4种配置方案：配置1，锂离子电池单独运行；配置2，锂离子电池与超级电容器共同运行；配置3，锂离子电池和超导磁共同运行；配置4，锂离子电池与飞轮储能共同运行。配置方案的功率与容量分布情况如表2所示。为验证哪一种配置方案更加合理，可以通过其成本之间的差异进行选取，储能全周期寿命为10 a。将其带入混合储能选型模型，所得的成本情况如表3所示。

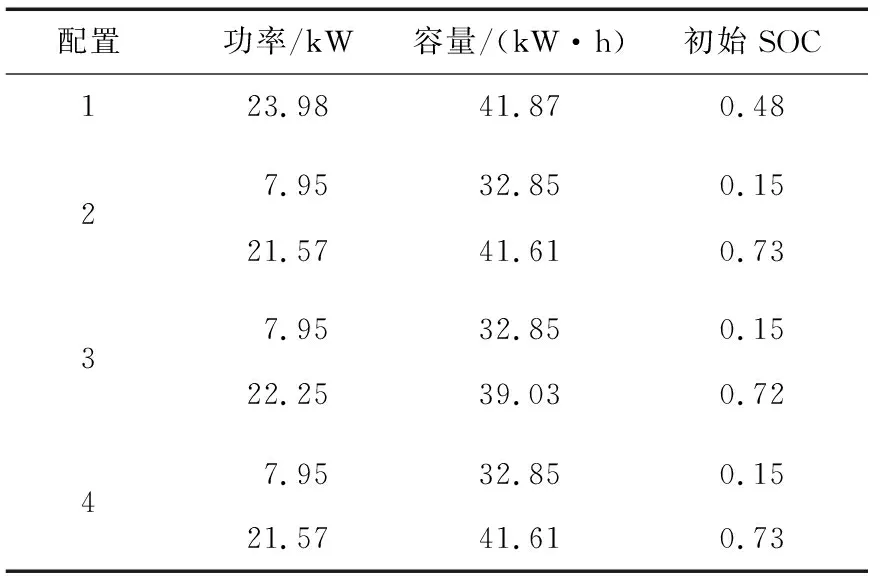
表2 不同配置方式下储能功率与容量Table 2 Energy storage power and capacity under different configurations mode

由表3可知，4种储能方式中锂离子电池与超级电容器的组合成本最低，所以本文采用锂离子电池与超级电容器的混合储能方式。其中，锂离子电池作为能量型储能系统，超级电容器作为功率型储能系统。同理可以求得不同置信水平下的混合储能功率和容量如表4所示。

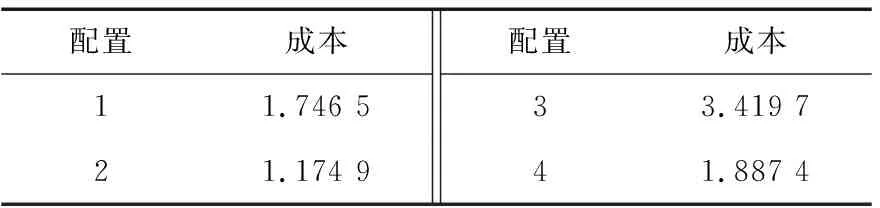
表3 不同配置方式下的储能成本Table 3 Energy storage cost under different configurations 亿元

表4 不同置信水平下储能功率和容量Table 4 Energy power and capacity at different confidence levels

由表4可知，在不同置信水平下，能量型储能系统的初始SOC均为0.15，是由于能量型储能在周期内最小充电电量为0，由式(18)可知其值不变。功率型储能系统的初始SOC也变化不大，置信水平在84.38%、87.50%和90.63%时都趋于0.65变化；置信水平在93.75%、96.88%和100%时都趋于0.73。整体而言，能量型储能初始SOC相对较低，功率型储能初始SOC相对较高。储能功率与容量基本都是随着置信水平的增大而增大，仅当置信水平从87.50%变化到90.63%时，能量型储能系统功率有所降低，这与混合储能功率分配有关。

6 结语

本文在研究混合储能平抑风电的过程中考虑了置信水平，从而得出以下结论。

1)通过幅频特性曲线选择截止频率能够在相同储能配置下使风电更为平滑。

2)适当的减小置信水平可以降低储能配置的容量和功率。

3)依据储能成本进行储能选型可使储能配置更加经济，更加客观。

考虑置信水平的混合储能平抑风电波动能以实现较小的投资成本获得最大化的平滑效果，为今后储能参与新能源消纳提出了新的解决思路，具有一定的指导意义。