低轨卫星通信信号捕获方法与实现*

祝 毅，高 波，鲁国林，刘明凯

（重庆两江卫星移动通信有限公司成都分公司，四川 成都 610096）

0 引言

随着移动通信的发展，低轨卫星通信正成为全球通信领域的热点方向，也被我国纳入新基建范畴。低轨卫星通信不仅能有效补充地面通信覆盖率，带动数字产业升级，实现经济和技术的高质量发展，还将成为大国博弈的战略制高点[1]。我国的航空、海洋、铁路及林业、矿业、油气田、电力、边防等各行业，在大气层飞行空间、海洋、荒漠、森林、山区等都有宽带移动通信的强烈需求。另外，我国企业在参与“一带一路”经济建设时，也需要信息通信技术的支撑。因此，当前我国发展低轨卫星通信的需求是现实和迫切的[2]，加速发展低轨卫星通信产业，研制低轨卫星通信设备十分必要。

目前的低轨卫星通信一般为多频时分多址接入（MultiFrequency Time Division Multiple Access，MF-TDMA）体制。在TDMA 信号的通信过程中，最关键的在于信号的时间捕获。低轨卫星通信信号具有突发时间短，多普勒频移动大的特点。信号在经过星地远距离传输后，要在接收端准确恢复发送数据则需要准确估计时间、消除频偏影响，还要解决极低信噪比下的信号检测问题[3]。传统的做法多为在TDMA 信号上加入一段特征码作为导频序列，通过滑动相关的方式捕获突发帧，但是该方法无法消除频偏影响，在复杂信道下亦不稳定。综合上述实际因素，针对信号捕获算法优化改进，并进行仿真分析，最后设计了基于现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）实现原理框图。

1 低轨卫星通信信号

采用TDMA 体制的卫星通信系统，会在时间上按照时隙为单位进行时间资源划分，多个时隙则组成一帧，帧和时隙会周期性地计数，所以无论是在接收端还是发射端都有一套本地的定时机制，它们都须以导航时间为基准同步[4]。

信号帧的格式如图1 所示，帧由时隙组成，而信号则分配固定的时隙长度。信号的空白填充为保护间隔用Pad 标识，中间由特征码和数据组成。当发送端的信号达到接收端时，经过处理时延和路径时延，接收到的信号不再是对齐时隙突发信号，因此接收端须对信号进行捕获，以准确估计信号的到达时间。

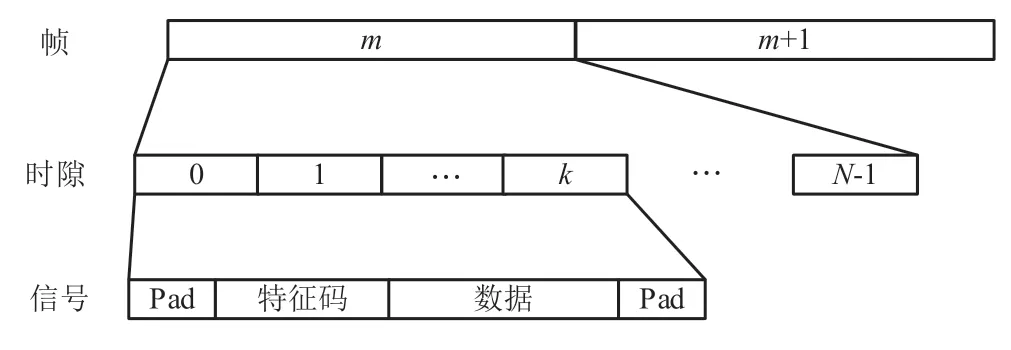
图1 信号帧格式

2 算法原理

2.1 信号捕获算法

如上文所述，传统方法对于接收到的一段突发信号需采用滑动相关[5]的方法来捕获信号，那么定义接收到的数字信号为：

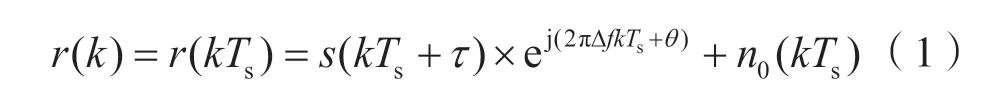
式中：r(k)为接收采样值；Ts为采样频率间隔；τ为收发延时；∆f为载波频偏；θ为相位偏差；n0(kTs)为噪声；k为采样离散点值。

假设特征码有L个符号，那么滑动相关窗的长度也应选择为L。相关时对接收信号段进行逐点滑动，滑动点应该从起始位置按符号间隔选取长度为L的点与本地特征码共轭相乘。一般情况下，采样频率是符号频率的M倍，那么选择的相关点为：

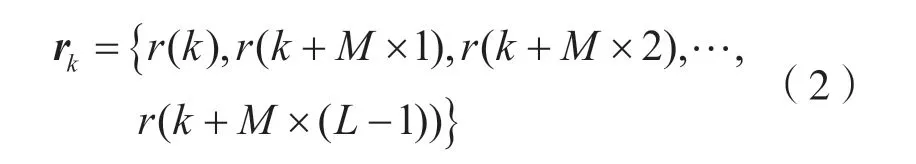
式中：k∈[-d,d]为接收信号滑动区间；d为滑动区间的边界范围。

接收信号与本地序列共轭相乘得到相关值：

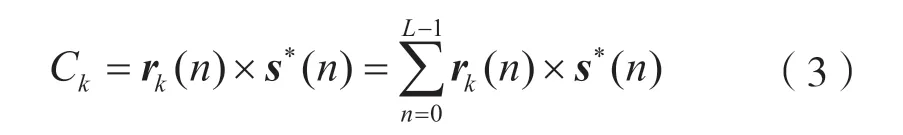
式中：s*(n)为原始发送向量共轭；rk(n)为接收向量；Ck为相关值；s(n)为发送原始样值；n0(n)为白噪声。将式（1）代入（3）计算得到：

根据滑动相关理论可知，当本地码与接收码对齐时可获得最大相关峰，即式（4）中第一项的求和最大。由于第一项在求和时还有一个频偏因子，所以其相关求和结果必定会受频偏的影响，这项频偏因子也是星地传输过程中不可避免的，它包含多普勒频偏和收发时钟偏差。再观察第二项，只有当噪声服从随机分布且L足够大时，相关求和项才趋近于0。实际情况中，为了保证数据传输效率特征码不可能很长，所以式（4）中第二项也会影响最终相关求和的结果。

下面将对式（4）中两个相关求和因子展开相关推导分析。

令：

式中：ck(n)为带频偏影响的相关因子；zk(n)为噪声与发送向量的相关因子。

2.1.1 方法1：延迟共轭差分方法

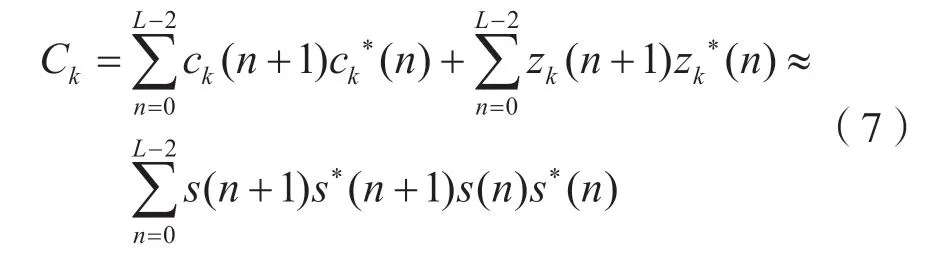
从式（7）可以看出，第一项消除了频偏的影响，第二项也改善了噪声的影响。

2.1.2 方法2：FFT 峰均比搜索方法

从频域的角度出发，对相关以后的序列做快速傅里叶变换（Fast Fourier Transform，FFT）运算得到一组频域数据[8-10]。在频域上噪声将会按照概率分布变成底噪，而相关项Ck(m)将在本地码与接收特征码对齐时出现较大峰值，这样就可以在搜索区间内找到到达时间（Time Of Arrival，TOA）位置。对相关式（4）做离散傅里叶变换：

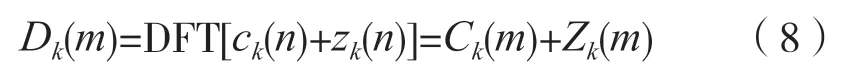
式中：DFT[]表示离散傅里叶变换。

为了方便判断比较，采用峰均比[11]作为比较因子，先计算滑动区间内的Tk，再求最大的Tk，则此时k所对应的索引a便是接收到信号的TOA 索引位置，具体的表达式为：

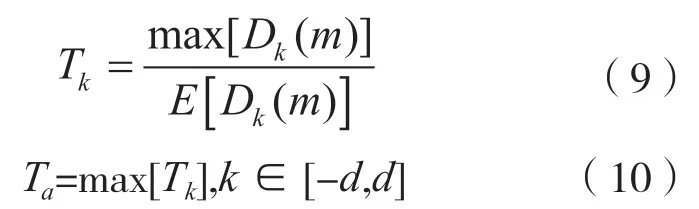
式中：Ta为信号达到位置的索引。第3 节将通过MATLAB 仿真来对比上述方法的性能。

2.2 定时精估计算法

上述的信号捕获算法虽然找到了接收信号的TOA 位置，但是该点却不是最佳采样点，这是因为数字上的采样是离散的和随机的。对一个符号内的采样，其最佳点应该是眼图的顶点，通过相关找到的TOA 位置只是位于最佳采样点的附近，所以需要进一步估计最佳采样点，而最理想的方法就是插值算法[12,13]，如图2 所示，需要获得插值系数分数间隔μk进一步估计最佳采样点。

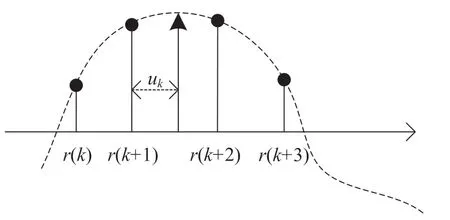
图2 分数倍插值

数字平方滤波定时频域算法指出，基带采样数据模平方及其频谱分量中含有采样时间信息，采样数据采样点的定时误差在频域可以表示为该频谱的相位旋转，通过对模平方序列进行DFT 计算得到该频谱分量的相位，进而求取定时误差[14]。

先对接收序列求模的平方：

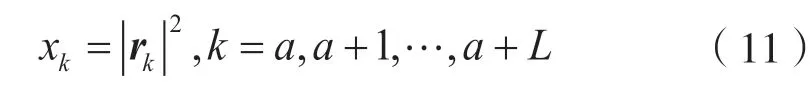
式中：a为TOA的起始点。

然后计算以a为起始点序列的傅里叶系数：

估计定时误差[15]为：

虽然抛物线插值更佳，但是为了方便工程实现，这里采用线性插值，插值系数分数间隔的计算方式为：

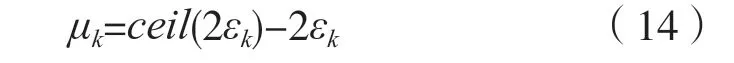
式中：ceil()表示向上取整。

在精确定时估计时，内插点的起始位置需根据定时估计调整前一个点或后一个点，新的TOA 估计点为：

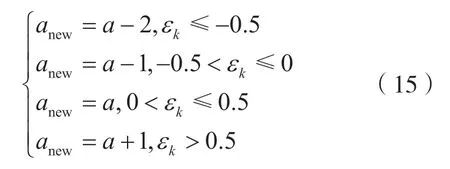
则插值以后的新序列表示为：

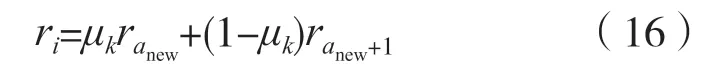
通过上述符号精估计算法，可以获得较为接近最佳采样点的估值，星座图上的点也会更加收敛。

3 算法仿真

根据实际应用场景对算法进行MATLAB 仿真。首先对方法1 和方法2的捕获性能进行仿真，设置如下条件下的仿真场景：

（1）条件1：设定符号信噪比Es/N0=5.5 dB时，符号速率16 ksps，频偏4 kHz，500 万次仿真，特征码长度20，用延迟共轭差分方法，搜索窗宽50，捕获失败的概率小于3.1×10-4。

（2）条件2：设定Es/N0=5.5 dB 时，符号速率16 ksps，频偏4 kHz，500 万次仿真，特征码长度20，用FFT 峰均比搜索方法，搜索窗宽50，捕获失败的概率小于1.5×10-5。相关窗如图3 所示。

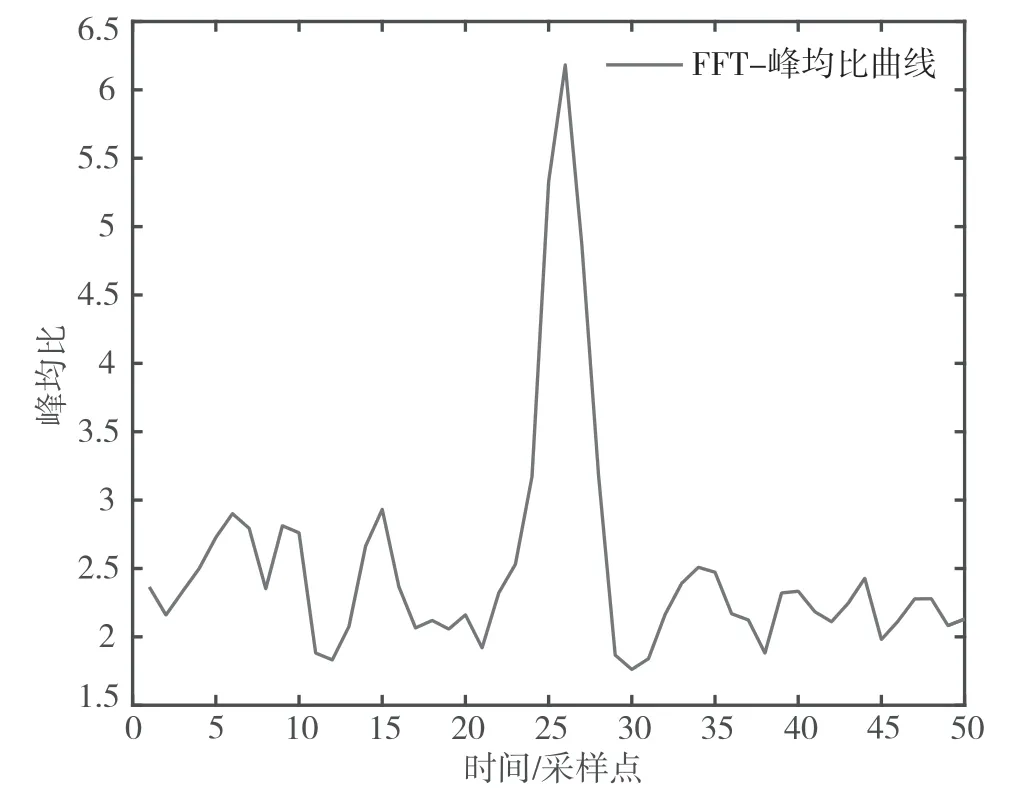
图3 FFT 峰均比搜索相关曲线

（3）条件3：设定Es/N0=-2 dB 时，符号速率30 Msps，频偏650 kHz，500 万次仿真，特征码长度1 024，搜索窗宽50 000，捕获失败的概率小于2×10-7。相关峰搜索如图4 所示。

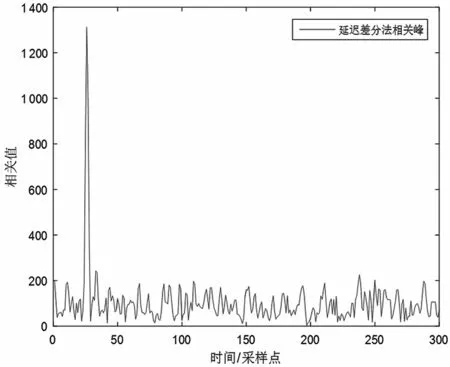
图4 延迟差分相关曲线

然后仿真对比精确定时前后的星座图，分别如图5 和图6 所示。

从图5 和图6 中可以看出，精确定时前的星座图比较发散，经过精确定时估计以后的星座图更加收敛，也更有利于后续解调译码处理。

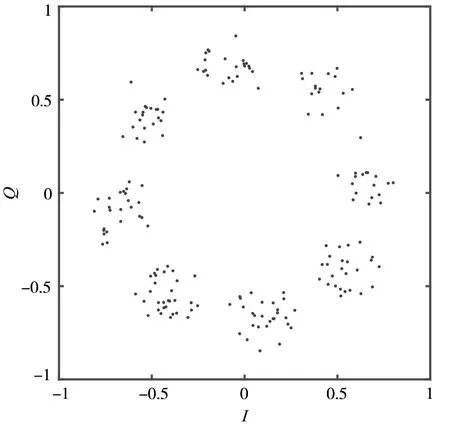
图5 精定时前星座

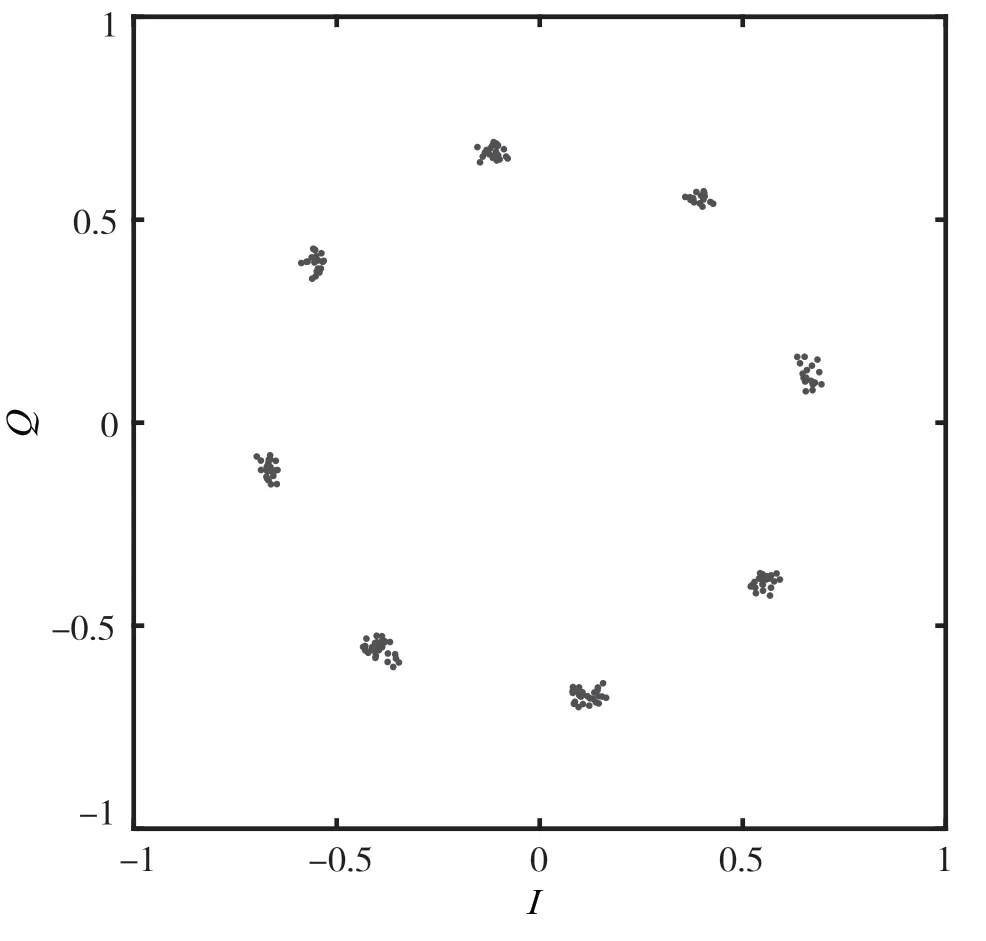
图6 精定时后星座

4 基于FPGA的算法实现

为了更好地指导工程应用实现，下面给出基于FPGA 实现的卫星通信信号捕获原理框图[16]。前级接收到的突发帧存于块存储器BRAM（Block RAM）当中，与本地特征码进行滑动相关。如图7所示为方法1的FPGA 实现原理图，其中，*代表共轭，D 代表延迟，MUX 为比较选择，CRT 模块为计数控制滑动相关，REG 为缓存寄存器。图8 为方法2的FPGA 实现原理图，其中，FFT 为快速傅里叶变换，avg 代表求均值操作，DIV 为除法操作。

图7 方法1的FPGA 实现原理

图8 方法2的FPGA 实现原理

上述两种实现均是串行流处理，如果希望提高处理速率可以对相关处和FFT 运算进行并行改进，如图9 所示。

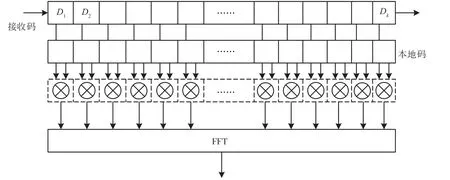
图9 并行改进FPGA 实现原理

定时精估计的FPGA 实现设计原理如图10 所示，从RAM 中读数进行求模处理。图10 中，arg符号求角度可以用坐标旋转数字计算（Coordinate Rotation Digital Computer，CORDIC）算法，这也适合FPGA 实现。Ceil 符号代表μk=ceil(2εk)-εk。

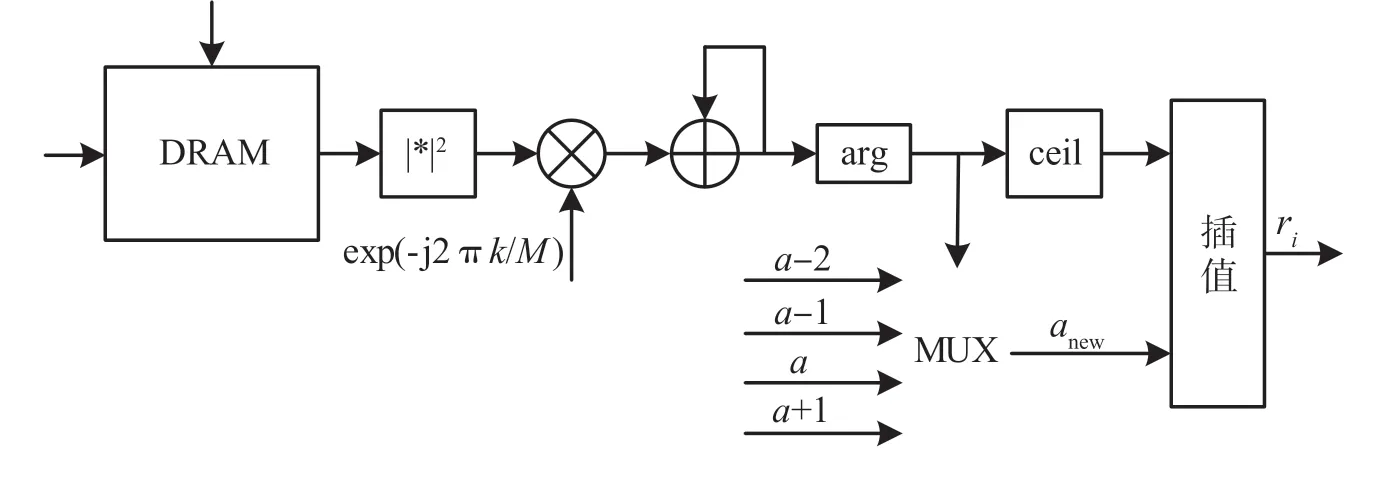
图10 精定时估计FPGA 实现原理

通过编程设计，上述算法在V7 系列690T 型号的FPGA 上实现的资源需求如表1 所示。表1 中LUT 为查找表资源，DSP 为乘法器资源，BRAM 为块存储器资源。

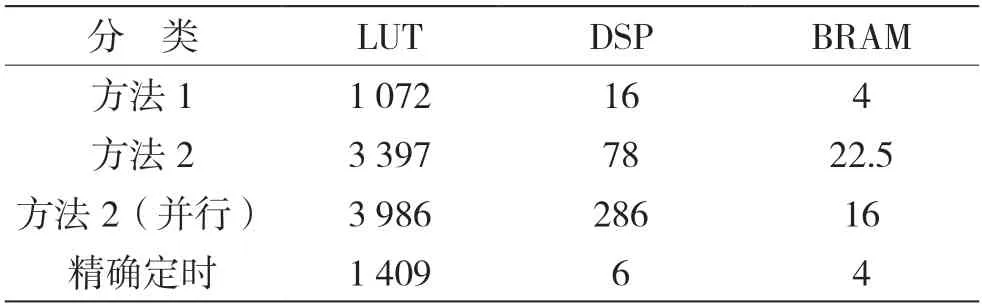
表1 资源消耗情况

5 结语

本文通过对低轨卫星通信信号捕获算法的研究和仿真，设计出了基于FPGA的实现原理。由在不同参数场景下进行仿真的结果以及FPGA 综合编译实现资源对比可以发现：方法2的捕获信噪比更优但是实现更复杂，资源消耗更多；方法1 兼顾实现难度和资源消耗，且在特征码较长时性能也足以满足实际应用，可根据实际工程择优选取。在实际应用中，如果工程上需要更快的处理速度，则可以加入并行改进的设计。