SAR 图像去噪的非局部均值算法改进*

陈 前，刘本永

（贵州大学，贵州 贵阳 550025）

0 引言

合成孔径雷达（Synthetic Aperture Radar，SAR）是拥有一定地表穿透性能的对地观测系统，进行观察时不受各种气候影响，已经被运用到多个领域。然而，SAR 图像中存在着一种固有的被称为散斑的噪声，这是由于其成像机理所导致的[1]，这些噪声会严重降低图像的标准，并对图像特征的提取和应用产生影响[2]。所以，在解释SAR 图像前，去除散斑噪声是不可或缺的一步[3]。

SAR 图像降斑的关键在于，在抑制散斑噪声的同时，保持图像结构信息。SAR 图像去噪方法主要包括空间域和变换域滤波技术两类[4]，其中空间域滤波包括Lee 滤波[5]、Kuan 滤波[6]和Frost 滤波[7]等。空间域滤波技术的基本方法是计算滤波窗口内中心点空间内像素的加权平均值，并使用计算结果作为中心点像素的估计值。空域法利用局部信息进行去噪，较好地抑制了散斑噪声，但去噪结果显得过于平滑，图像细节信息被丢失。相较于空域法，变换域法利用多尺度分析，在抑制噪声和保留细节方面都有较好的性能，常见方法有小波变换[8]、Contourlet 变换[9]等。然而，以上两类方法没有结合图像自有的结构数据来进行去噪。Buades 等人[10,11]提出了一种非局部均值（Non-local means，NL-means）算法，用于处理自然图像中的加性白噪声。该算法的基本思想是，在搜索框中通过比较相似框和以待估计像素为中心点的目标框之间的相似性，来确定对应像素的权重。近几年，有学者在此基础上进行了改进，并在图像去噪方面取得了一些成绩。Deledalle 等人[12]基于图像块的概率分布（Probabilistic Patch-Based，PPB）提出了加权平均噪声消除算法。在三维块匹配（Block Matching 3D，BM3D）算法的启发下，Parrilli 等人[13]将局部线性最小均方误差（Nonlocal Linear Minimum Mean Square Error，NLMMSE）准则和非抽样小波相结合，提出了SAR-BM3D算法，用于SAR 图像去噪。易子麟等人[14]为了改善图像块之间的相似性测量，提出了结合结构相似性指数的改进算法。

针对SAR 图像散斑噪声的特点，本文提出一种改进的非局部均值（Non-Local means，NL-means）算法来进行SAR 图像降噪。该去噪算法包含4 个处理步骤：

（1）将原始图像转换为对数图像；

（2）在对数图像上进行高斯滤波；

（3）采用所提改进算法进行滤波；

（4）将对数去噪图像转化为初始空间图像。

去噪结果表明，该算法在处理实际SAR图像时，能够有效抑制散斑噪声，更好地保持图像细节。

1 SAR 图像噪声模型

一般假设SAR 图像中的散斑噪声是乘性噪声[15]，可表示为：

式中：X为带噪SAR 图像；u为地物真实值；v为散斑噪声。

首先，采用对数工具对图像进行处理，变换公式为：

2 非局部均值算法

NL-means算法利用图像自身的冗余特性，对相似块和目标块进行测量，得到权重，再将相应的像素与其权重相乘并计算平均值，求出目标块的中心点像素值。算法框架定义为：

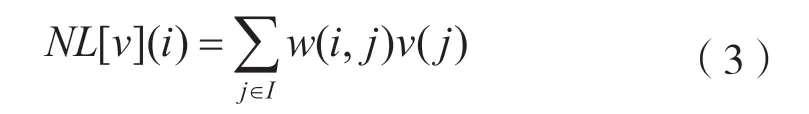
式中：v(j)为图像块中类似于像素i的像素；权重w(i,j)根据像素i与像素j的相似性来决定，0 ≤w(i,j)≤1且。

像素i与像素j之间的相似性由高斯加权欧氏距离d(i,j)来计算，其表达式为：

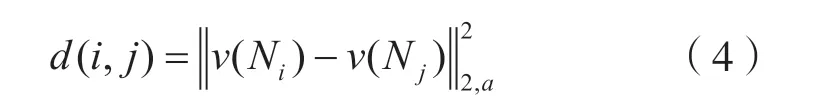
式中：Ni表示中心点在像素i上的一个固定尺寸的正方形邻近区域；Nj代表一个中心点为像素j的固定尺寸的正方形邻近区域；a表示高斯核的标准差，且a>0。高斯加权欧几里得距离越小，图像中的相似性就越大，对应的像素点的权重也就越大，权重定义为：

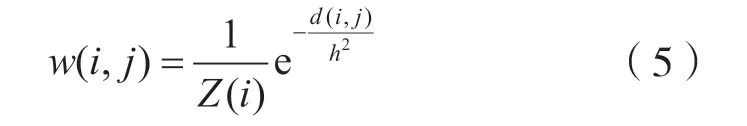
式中：Z(i)为标准化常数；参数h控制函数的衰减速度。

3 改进的非局部均值算法

传统的NL-means算法对图像同质区域的噪声去除结果较好，但是对于结构信息，如边缘和纹理，去噪结果是模糊的，这通常是由于NL-means算法中测量块之间的相似性仅考虑了灰度值信息，而不适用图像本身的结构数据。由于高斯加权欧式距离较大，边缘和纹理区域中与目标块结构相似的块也可能被赋予较小的权重，导致最后的结果差，不能很好地去除散斑噪声。为解决这一问题，考虑在NL-means算法中引入高斯加权的空间距离，并与原有的高斯加权欧式距离结合构成新的相似性度量指数。本文改进算法的结构如图1 所示。

图1 改进的NL-means 滤波器流程

针对使用高斯滤波处理图像会导致边缘模糊的问题，Tomasi 等人[16]基于高斯滤波，将图像的像素范围域信息和空间域信息作为两个高斯核函数进行非线性组合，提出的双边滤波能很好地保持图中的结构数据。在双边滤波中，根据对应点的像素值的加权组合来确定待估计点的像素值，因此权重是空域核和像素域核的组合，其表达式为：

式中：(||p-q||)为空间域核；(|I(p)-I(q)|)为像素范围域核；Wp为归一化常数；p为滑动窗口的中心点；q为滑动窗口内的任一点；I(p)为像素点p的像素值；I(q)为像素点q的像素值；σs为空间域标准差；σr为像素范围域标准差；S为滑动窗口的范围。空间距离是指从滤波窗口内对应点到中心点的欧几里得距离。空间域核的函数表示为：

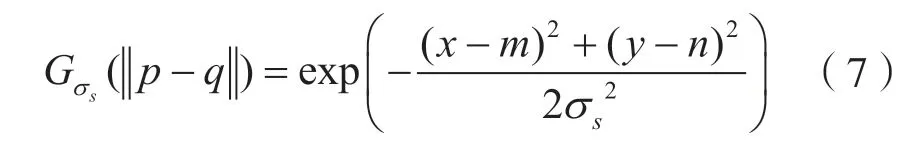
式中：(x,y)为滤波窗口当前点位置；(m,n)为滤波窗口中心点位置；σs为空间域标准差。灰度距离表示滤波窗口内对应点与中心点之间灰度差异的绝对值。像素范围域核的函数表示为：

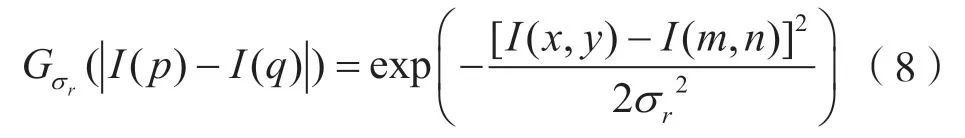
式中：I(x,y)为在滤波窗口内的当前点的像素值；I(m,n)为在滤波窗口内的中心点的像素值；σr为像素范围域标准差。

本文引入高斯加权的空间距离，和原高斯加权的欧氏距离组合，改进NL-means算法的块相似性度量指数。所提方法通过对与目标块结构类似的块进行加权处理，以达到增强边缘和纹理的目的，从而保持图像的细节信息。

高斯加权的空间距离可表示为：

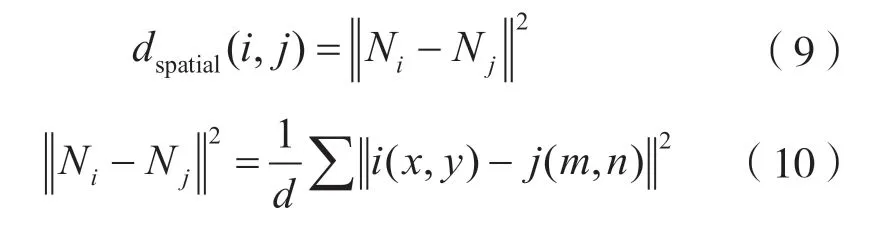
式中：Ni代表一个中心点在像素i上的固定尺寸的正方形邻近区域；Nj表示一个中心点在像素j上的固定尺寸的正方形邻近区域；i(x,y)和j(m,n)表示像素点坐标；d是高斯加权的距离核函数，其特征是离中心点越远权重越小。

通过以上的修改，把式（9）和式（4）组合，然后代入式（5）中，可得到一个全新的相似性度量指数：

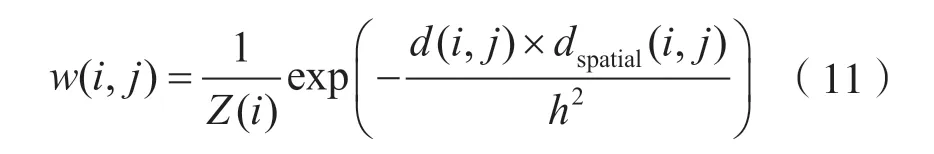
式中：Z(i)为标准化常数；参数h控制函数的衰减速度。

最后采用指数变换的方式处理去噪结果，将其转换为初始空间的去噪图像。指数变换公式为：

式中：为由所提算法处理后的对数去噪图像；为初始空间去噪图像。

4 实验及结果分析

4.1 实验数据和参数设置

在两幅实际SAR 图像上进行仿真实验，验证所提出算法。实验数据1 是一幅大小为512×512像素的城市场景SAR 图像，用SAR1 表示；实验数据2 是一幅大小512×512 像素的机场场景SAR 图像，用SAR2 表示。

对比实验分别实现了传统的Lee 滤波算法、Kuan 滤波算法、Frost 滤波算法、经典NL-means去噪算法和本文提出的改进NL-means 去噪算法。Lee 滤波器的过滤窗尺寸设定为3；Frost 滤波器的滤波窗口大小设置为5；经典NL-means 滤波器的相似框大小设置为7×7，搜索框的大小设置为21×21[3]，滤波参数h为4.5；本文改进NL-means滤波器的相似框大小设置为3×3，搜索框大小设置为11×11，滤波参数h为4.5。

4.2 去噪效果评价指标

4.2.1 峰值信噪比

峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）反映初始图像与已处理图像之间的畸变程度。PSNR值越大，代表失真越少，定义为：

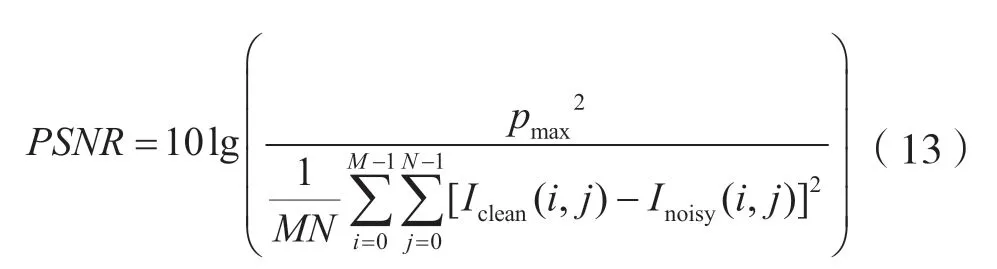
式中：pmax为图像像素灰度值的最大值；Iclean为干净图像；Inoisy为噪声图像；M为图像的高度；N为图像的宽度。

4.2.2 结构相似性

结构相似性（Structural Similarity，SSIM）[17]从图像亮度、对比度和结构数据等方面考虑初始图像和处理后的图像之间的相似程度。SSIM的范围为[-1,1]，SSIM值愈接近1，两幅图像的结构愈相似。SSIM函数表示为：

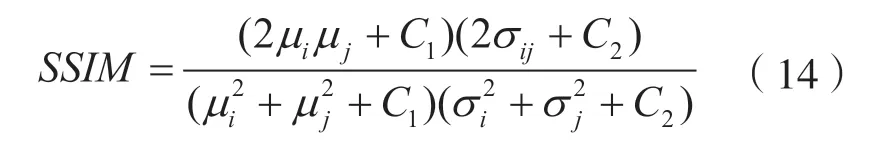
式中：μi和μj分别为像素i和j像素值的均值；σi和σj分别为像素i和j像素值的方差；σij表示图像之间的协方差；C1和C2为常数。

4.2.3 比值图像

将原图像X和去噪图像之间逐点进行比较就得到比值图像（ratio image）[18,19]。比值图像中包含的结构数据，如边缘和纹理越少，噪声分布越均匀，表明噪声去除效果越好[20]。同时，求取比值图像的方差Dratioimage，以更直观的方式比较结果好坏。

4.3 实验结果

对两幅实际SAR 图像进行了实验，得到了如图2 和图4 所示的去噪结果，并给出了对应算法的比值图像如图3 和图5 所示。

不同算法的去噪结果如图2 和图4 所示，通过观察比较可知，Lee 与Frost算法去噪效果过度平滑导致图像模糊，而Kuan算法去噪效果不够平滑，NL-means算法与改进NL-means算法在图像平坦区域更平滑，并且图像不模糊。

图2 城市场景SAR 图像SAR1 及不同算法的去噪结果

图3 SAR1 用不同算法去噪后的比值

图4 机场场景SAR 图像SAR2 及不同算法的去噪结果

图3 与图5 为不同算法所对应的比值图像（为便于观察，该图中各像素值均放大了100 倍），对比两图可以看出：Lee、Kuan 与Frost算法比值图中保留了明显的结构信息，说明去噪能力不强；NLmeans算法的比值图中含较少的结构信息，而本文所提的改进算法的比值图像包含最少的结构信息，并且噪声的分布几乎是完全随机的，说明本文算法具有最有效的去噪效果。

图5 SAR2 用不同算法去噪后的比值

表1 与表2 分别展示了对不同算法在SAR 图像上去噪效果的客观评价。通过比较PSNR可知，本文所提算法的PSNR分别为32.127 1 dB 和31.941 2 dB，分别比其他算法高出1.505 8～12.817 8 dB与1.190 8～14.054 5 dB，说明所提算法在去噪过程中的失真率低。对比SSIM可以看出，所提改进算法的结构相似性分别为0.971 4 和0.952 6，均大于其他算法的结果，表明经过所提算法处理的去噪图像在结构上与初始图像更加相似，且边缘、纹理等结构信息保留更多。

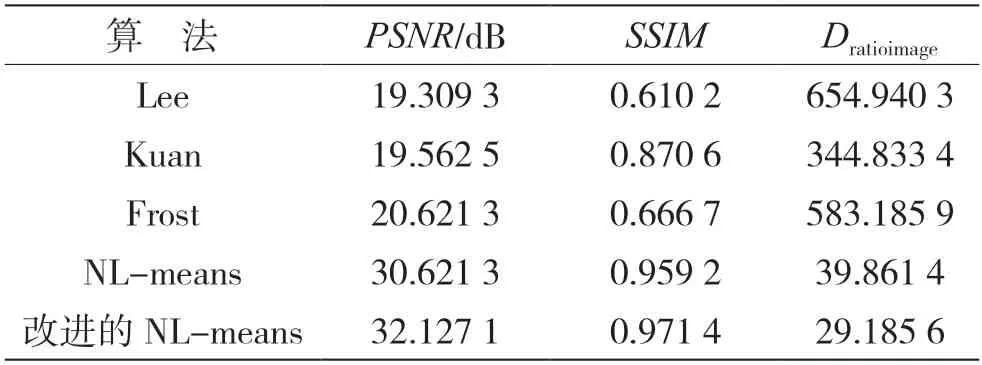
表1 不同算法在SAR1 图像上去噪效果的评价指标

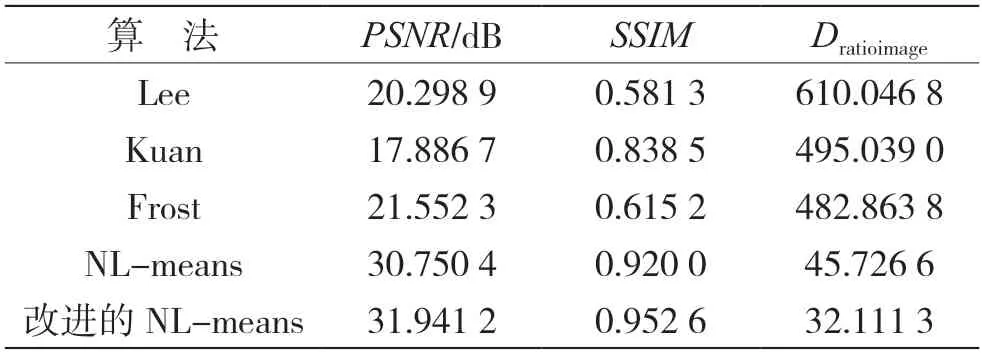
表2 不同算法在SAR2 图像上去噪效果的评价指标

综上所述，与其他算法相比，本文所提算法得到的去噪图像在视觉方面具有更好的效果，并且在PSNR、SSIM和比值图像等评价指标上的结果也更好。因此，本文的改进算法在散斑噪声抑制方面更加实用，在图像中有效地保留了结构数据。

5 结语

散斑抑制是SAR 图像处理的基础，在SAR 图像的进一步处理中起着至关重要的作用。针对经典NL-means算法在SAR 图像纹理区域去噪效果较弱的现象，探讨了基于NL-means的改进算法。具体的算法流程为：首先，通过对数变换的方式，SAR图像中的乘性噪声被重建成加性噪声；其次，使用高斯滤波进行初次滤波；再次，运用所提算法对初次滤波结果进行二次降噪；最后，在对数去噪图像上采用指数变换方法，使其转化为初始空间图像。然而，本文所提算法运算速度较慢，仅对场景内容简单的图像有较好的去噪效果，而对包含山地等场景内容图像的处理结果不理想。未来的工作将继续改进存在的问题。