一种基于Max-Log-MPA算法的改进方法*

陈宇祥，张 伟，吴思雨，周淑华

（南京邮电大学，江苏 南京 210003）

0 引言

在通信技术的发展历程中，多址接入技术是现代无线通信系统发展和演进的基础。当用户数量激增时，资源的正交性就受到限制，此时非正交多址接入（Non-Orthogonal Multiple Access，NOMA）技术成为新的关注点[1,2]。稀疏码多址接入（Sparse Code Multiple Access，SCMA）是NOAM 技术的代表之一，最早是由低密度扩频（Low Density Signature，LDS）技术发展而来[3]。无线通信系统从第一代无线通信发展到第四代无线通信，多址技术都是采用正交多址接入（Orthogonal Multiple Access，OMA）技术。OMA 技术因为资源受限，必然导致可接入的用户数目有限，正是这样，非正交多址技术也越来越受到关注。

SCMA 系统和LDS 系统较为类似，但在其基础上引入了多维调制技术，这种方式可以提升SCMA系统的增益[4,5]。SCMA 系统用户的码字存在稀疏性，这样就可以采用MPA算法进行检测[6]。本文提出一种基于相似度的阈值判断方式，以Max-Log-MPA算法为例，在取得合适的阈值的情况下来达到算法性能和复杂度之间的平衡，进一步降低算法的复杂度。

1 上行SCMA 系统模型

假设用户数目为J，同时向共享K个正交时频资源的同一基站传输数据，此时定义过载因子为，M为码本大小，简化的SCMA 模型如图1 所示。

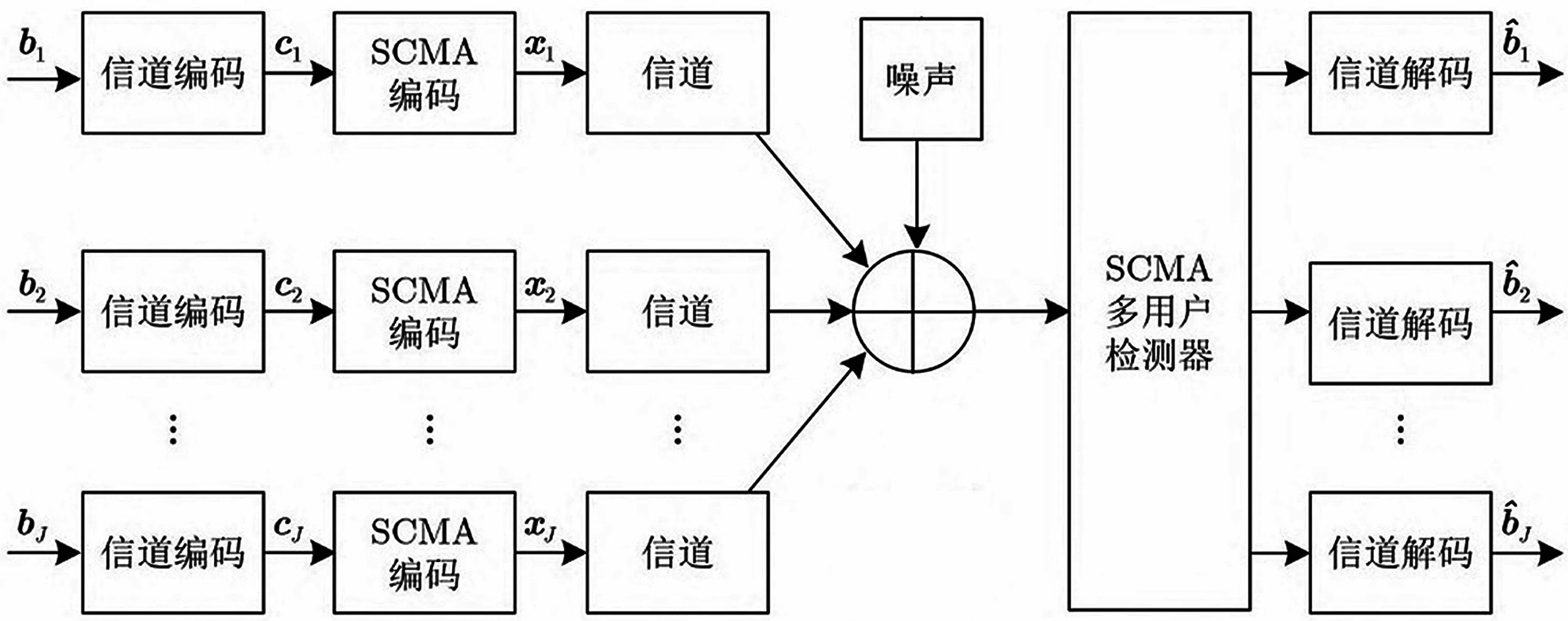
图1 简化的SCMA 上行链路模型

SCMA 系统编码映射过程如图2 所示，图中系统有6 个用户和4 个资源块，每个用户占用2 个资源块，每个用户都拥有特定的码本且码字具有稀疏性。

如图2 所示，每个码本是4×4的矩阵，其中只有2 行元素是非空白部分，表示为非0 部分，用户1 到用户6的用户码本的第4，2，2，0，1，4个码字参与编码。为了方便，本文采用F矩阵（因子矩阵）来表示这样一种结构，对应的F矩阵为：

图2 编码映射过程

式中：矩阵行代表资源数；矩阵列代表用户数。

定义dr=3，dv=2，其中dr为行重因子代表每个资源占据的用户数，dv为列重因子代表每个用户占据的资源数。由F可知，每行有3 个非零元素，每列有2 个非零元素，使用这种方式限制资源上的用户数用来减小用户之间的干扰，接收端用户信号为：

式 中：y=[y1,y2,y3,…,yK]T为用户的接收信号；hj=[h1j,h2j,h3j,…,hKj]T为 第j个用户的增益信息；xj=[x1j,x2j,x3j,…,xKj]T为第j个用户的码字信息；n为高斯噪声矢量。

一个综合题的解答往往蕴藏着较大的信息量，反思其过程，留心其中的一些数据，往往会得到意想不到的收获．下面以一道考题的一个解答为例，简析其中的数据关系，进而提出一个与矩形相关的命题，并给出几种证法．

2 MPA 和Max-Log-MPA 多用户检测算法

2.1 MPA算法

MPA算法节点分为用户节点（U）和资源节点（R），算法的每次迭代U和R都会参与，图3 是式（1）因子矩阵F对应的因子图。

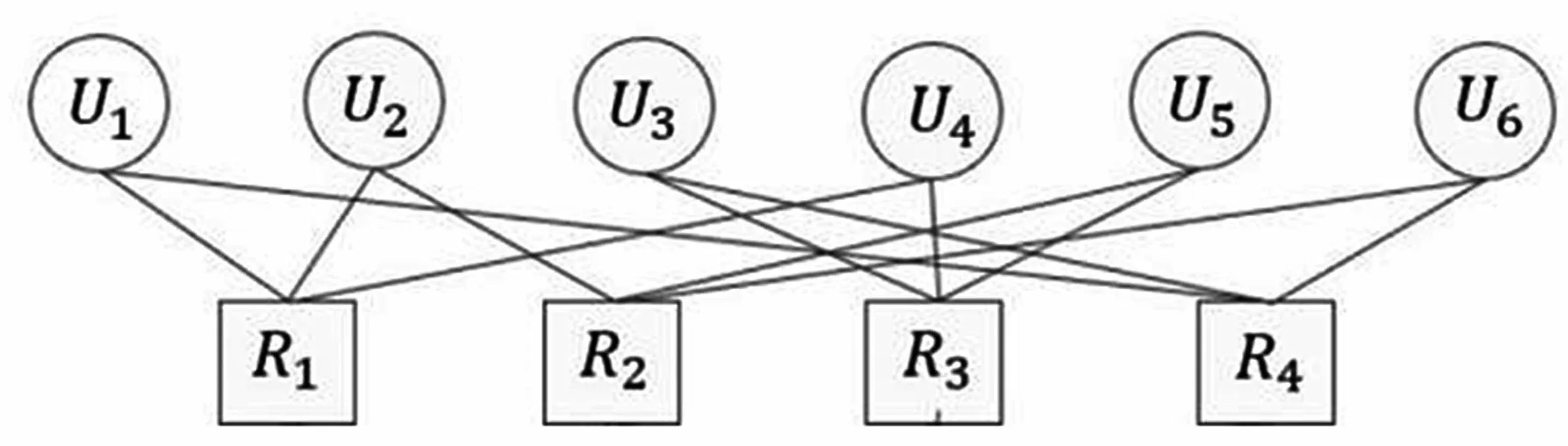
图3 因子图

xk,j为第k个资源上发送的符号，yk表示第k个资源上的接收信号，在第t次迭代中，定义为第k个资源节点向第j个用户节点迭代的消息值，定义为第j个用户节点向第k个资源节点迭代的消息值。其中，=(χ1×…×χJ)表示J个用户码本中所有码字的可能组合（M J）。

MPA算法的具体步骤如下[7,8]：

（1）对第一次参与迭代的码字xj进行初始化，ξj表示与用户节点相连的资源节点集合：

（2）资源节点的消息更新，计算资源节点k向用户节点j传递的信息：

式中：集合表示用户节点在资源节点k上所有资源节点，但是不包括用户节点j；ξk集合表示资源节点和用户节点相连的节点。

（3）用户节点上消息更新：

式中：ξjk集合表示用户节点j与其关联的资源节点，自身资源节点k除外。

（4）当t=T=tmax时，译码完成，码字概率的计算方式为：

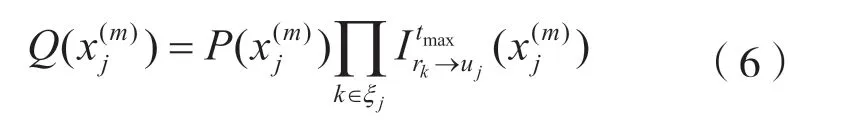
2.2 Max-Log-MPA算法

Max-Log-MPA算法通过数学方式和近似估算[9]，将指数运算转变为计算复杂度相对较低的求最大值运算，从而算法的复杂度大幅下降，但是这种方式也必然会造成消息的丢失，导致检测性能相对较差[10]。

运用Jacobi算法公式可得：

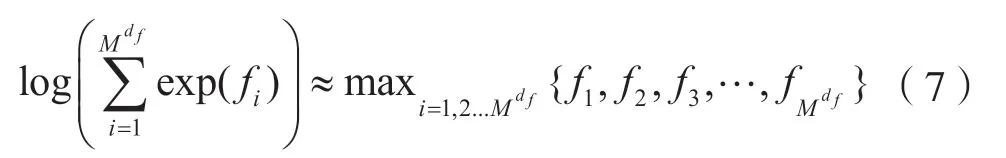
式中：df表示资源节点的用户数。则有：

进行最大迭代之后，每个用户码字输出的概率为：

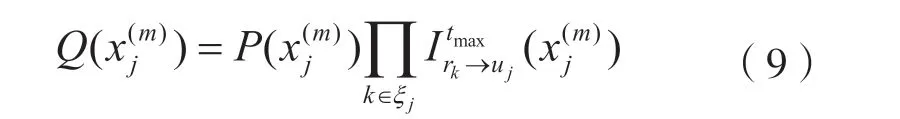
从式（9）可以看出，这里的资源节点更新消息是采用近似估算的方式，即：

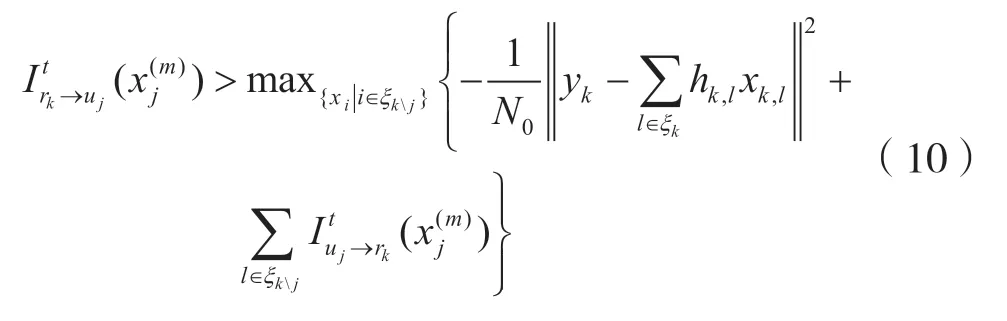
所以上述方法会有一定的性能丢失。

2.3 基于Max-Log-MPA算法的复杂度优化

在Max-Log-MPA算法的基础上，定义相似度：

式（11）表示上一次迭代和本次迭代之间的相似程度，这里的相似度可以看成一种阈值，当迭代的相似度达到对应的阈值时，就可以将本次迭代的用户信息用上次迭代的信息代替，即：

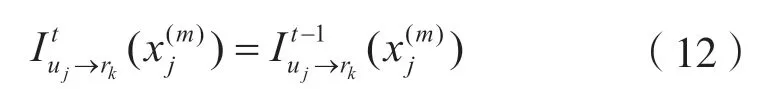
然后参与下一次迭代，当相似度阈值越大时，每次进行用户信息迭代时忽略本次迭代的可能性越大，即造成的性能丢失越大；当相似度阈值越小时，每次进行用户信息迭代时忽略本次迭代的可能性越小，即造成的性能丢失越小。当相似度阈值小到足够每次迭代都能参与本次的用户迭代时，本算法就等价于Max-Log-MPA算法。因此，可以采取统计的方式来记录相似度阈值，选择合适的阈值区间。这种算法的优势是可以在复杂度和算法性能之间取舍，降低一定的性能来换取算法的可实现性，减少迭代的复杂度。

3 仿真结果

MPA算法的误比特率（Bit Error Ratio，BER）性能和信噪比的变化曲线如图4 所示，算法复杂度在迭代过程中主要取决于步骤2 和步骤3，因此算法的复杂度优化也主要集中在步骤2 和步骤3。系统仿真信道采用了瑞利（Rayleigh）信道，最大迭代次数tmax分别为1，2，4，8。在Rayleigh 信道下，相同信噪比下系统迭代次数逐渐变大时，MPA算法的误码率性能会逐渐提升。图4 中当BER 为10-2false 时，最大迭代次数为tmax=2 时，MPA算法相比tmax=4 性能损失约1.3 dB，算法随着迭代次数的增加逐渐收敛。由于算法收敛后判决值更精准，BER 性能也就更好。

图5 给出了MPA算法和Max-Log-MPA算法在不同的tmax下的BER 性能变化曲线，仿真信道采用了Rayleigh 信道，系统的最大迭代次数tmax分别采用1，2，4，8。从中可以得出Max-Log-MPA算法和MPA算法一样，随着系统最大迭代次数的增加，BER 性能会有所提升；但是在tmax相同的时，相同BER 下MPA算法的信噪比丢失是比较大的。

图5 Max-Log-MPA算法误码率曲线

Max-Log-MPA算法的复杂度优化仿真结果如图6 和图7 所示。图6 中给出了tmax=10的情况下，相似度阈值从2 到1的BER 性能变化。图7 展示了相同信噪比的情况下，BER 性能随迭代次数的变化曲线。从图6 中可以看出，随着相似度从2 逐渐下降到1，BER 也会随之下降，其中在相似度V=1时，在相同的tmax下，本文所提算法的BER 性能和没有设置相似度的算法接近。在BER 为7.8×10-2时，V=1，V=1.1 和没有设置相似度的算法性能损失最大接近0.1 dB。从图7 中可以看出，相似度V∈[1,1.6]时BER 差距在7×10-3之内，其中，当V=1 时，本文算法和没有设置相似度的算法收敛性能曲线BER 差距在10-3之内。以上仿真实验得到的结果说明，可以在不同的相似度之间取舍，选择合适的算法复杂度和性能。

图6 Max-Log-MPA算法不同的相似度误码率曲线

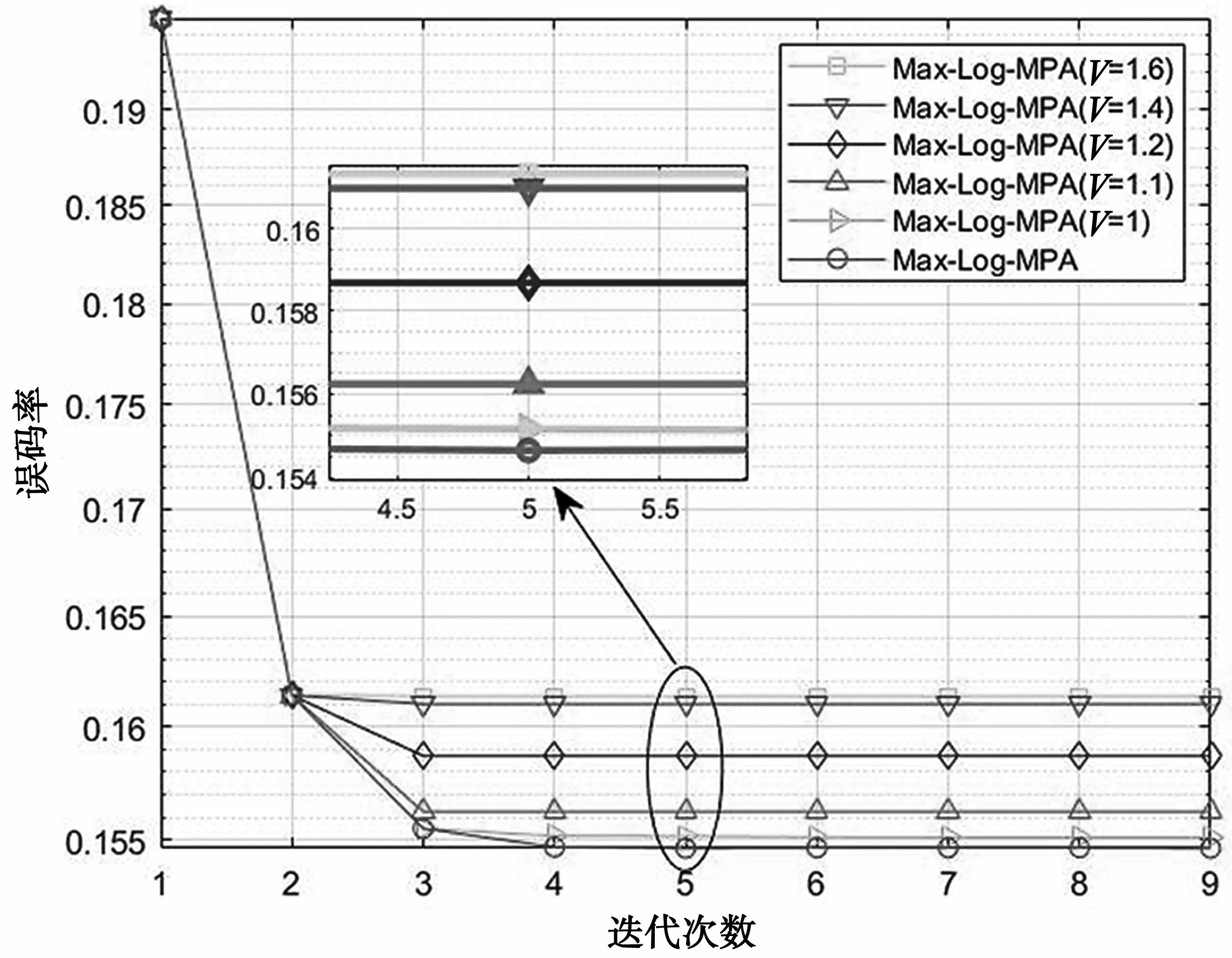
图7 Max-Log-MPA算法不同相似度收敛性能曲线

4 结语

SCMA 系统作为NOAM的关键技术之一，大量学者针对降低SCMA 系统检测算法的复杂度进行了研究。本文从MPA算法和Max-Log-MPA算法入手，分别对MPA算法和Max-Log-MPA算法进行了原理剖析，并对比了它们的性能，然后提出了基于Max-Log-MPA算法的一种改进方法并进行了仿真对比。本文提出的方法利用合理的相似度阈值来提高算法的性能，降低了算法的复杂度。该方法并不只是适用于Max-Log-MPA，还可以应用于其他算法，只要通过统计方式选择合适的阈值并在对应算法复杂度和性能之间做出取舍，就可以处理具体的问题。