一种基于深度学习的民航GPS 干扰识别方法*

鲁东生，黄 琳，龙 华

（1.昆明理工大学，云南 昆明 650100；2.云南省无线电监测中心，云南 昆明 650100；3.云南省科学技术院，云南 昆明 650100）

0 引言

近年来，随着我国经济社会的快速发展，民航运输业发展迅速，民航全球定位系统（Global Positioning System，GPS）信号受不明无线电干扰的事件也频频发生。由于GPS 在民航领域的应用十分普遍，所以不明无线电干扰对飞机飞行安全造成了严重威胁，也给广大人民群众的生命财产安全带来巨大的隐患[1-4]。因而，识别GPS 干扰信号对于无线电监测和干扰排查显得十分必要。

现有研究表明，信号特征的提取方法和分类算法的设计对干扰识别的准确率有直接影响。在特征提取方面，Kang 等人[5]采用自适应陷波器和自适应级联滤波器来识别GPS 信号中的单音、多音、扫频连续波干扰和带限高斯白噪声的特征，这与滤波器的设计密切相关。许永毅[6]则采用观察频谱的方法来提取干扰特征，但该方法严重依赖于人工经验。陈必然等人[7]利用受欺骗的信噪比与正常卫星的信噪比不同这一特征，通过模糊聚类的方法来判断GPS 欺骗式干扰。史文森等人[8]则利用GPS 信号的空域特征，结合接收机的波达方向（Direction Of Arrival，DOA）数据来识别GPS 欺骗式干扰。但以上两种方法的识别类型有限。张婧等人[9]针对典型的GPS 干扰信号，提取了8 个特征，并设计了反向传播（Back Propagation，BP）神经网络和支持向量机分类器，在干信比为3 dB 时，对于部分噪声干扰的平均识别率较高，但是该研究缺乏实际数据作为支撑，且未考虑干扰叠加的影响。

笔者考虑到典型GPS 干扰在时频域的差异明显，在时频域提取相应的统计量，再结合深度学习网络在分类识别问题上的优异性能，期望解决复杂干扰叠加情况下的干扰识别问题。

1 GPS 干扰

根据实际无线电监测情况，可将民航GPS 干扰分为人为干扰、无意干扰[10]两类。从现有干扰案例来看，影响最大的是人为干扰，数量最多的是无意干扰，这些干扰严重时可造成用户无法正常捕获粗捕获码（Code Coarse/Acquisition Code，C/A），导致通信中断。人为干扰主要来自因个人隐私、敏感区域、无人机管控、军事对抗等特殊需要而人为架设的专用GPS 发射装置[11]。无意干扰包括频带内射频干扰、频带外射频干扰和环境噪声等，主要来自自然环境变化、接收机内部或近场电磁环境因素，以及其他人为非故意的无线电干扰，如故障无线电发射机或其他电子电气设备的电磁泄漏、谐波、杂散及发射机互调等。表1[12-13]给出了GPS 射频干扰的分类。

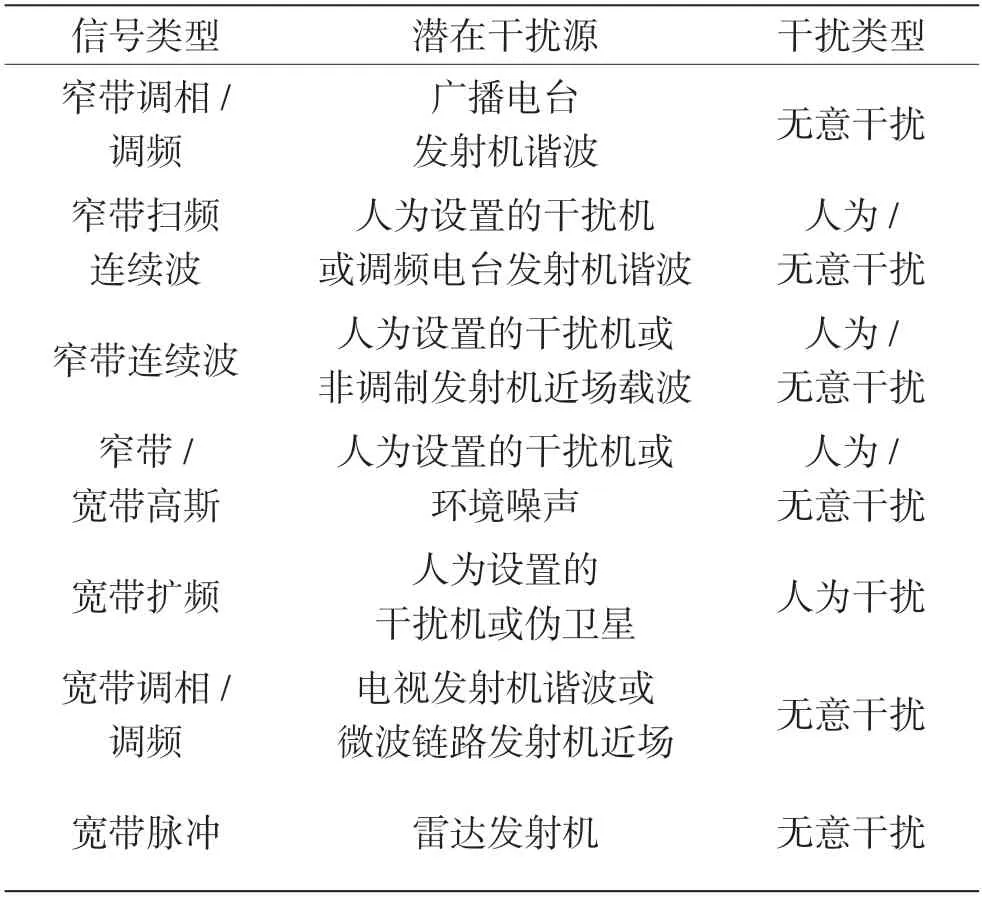
表1 典型射频干扰的信号分类

当接收机同时收到干扰信号与GPS 信号的叠加信号时：

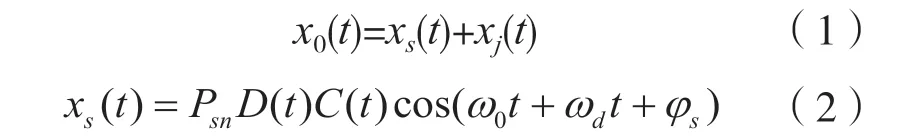
式中：x0(t)为叠加干扰后的信号；xs(t)为GPS 信号；xj(t)为干扰信号；Psn为受卫星信道衰落影响的归一化信号功率；D(t)为数据码序列；C(t)为扩频伪码序列；ω0和ωd分别为标称载频和载波多普勒频率；φs为服从[0,2π)上均匀分布的载波相位；t为时序。

则接收机输出为：

式中：Kn为第n阶系数。

假设接收系统是线性的，且不考虑接收机互调，则式（3）变为：

由于近地干扰源相对于被干扰对象的距离都远小于卫星与用户的通信距离，所以GPS 信号到达地球表面进入接收机前端的信号功率通常没有潜在干扰源的功率大[14]。此时，对于GPS 接收机而言，在不考虑机器内部噪声的前提下，输出干信比近似等于输入干信比，故利用干信比ε=20 lgUj/Us（Uj为xj(t)的最大电平值，Us为xs(t)的最大电平值）来调节干扰信号的强度。

若假设接收机收到的信号信息量为J(s+j,s)=H(s+j)-Hj（H(s+j)为干扰与信号之和的熵，Hj为干扰的熵）。当J(s+j,s)减小到某一阈值时，传输的信息将无法正常恢复，故在信号确定的条件下，增加Hj，可以减小J(s+j,s)，达到增加干扰效果的目的。根据香农定理，在功率受限情况下，服从高斯分布的噪声熵值最大，所以现实中，常把有限带宽的高斯噪声用作固定带宽的干扰。当噪声引起的误码率达到10%时，通信将遭到破坏。有限带宽的高斯噪声干扰可由高斯噪声通过带通滤波器获得，其数学模型为：

式中：f为调制频率；fc为载波频率；为双边功率谱密度；B为滤波器带宽。则干扰信号为：

宽带均匀频谱干扰是锯齿波宽带调频和噪声窄带调频相结合的干扰方式，其数学模型为：

式中：A为调频信号幅度；ω0为调频信号中心频率；Kf为调频指数；ϕ0为调频信号初始相位；Vs(t)为锯齿波函数。

噪声调幅干扰的数学模型为：

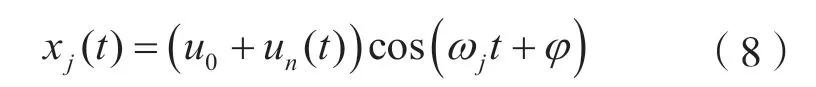
式中：u0为载波电平；un(t)为调制噪声，且E[un(t)]=0，D[un(t)]=σ2；φ为初相，服从[0,2π)上的均匀分布且与un(t)独立。

单频脉冲干扰[15]是一种呈周期状态、持续时间短且频带较宽的干扰。受其影响，误码率可能会增加，短时间内发生传输错误，影响通信系统的传输性能或导致系统无法正常工作。其数学模型为：

式中：uj为干扰信号电平；ωj为干扰信号频率；θ为干扰信号随机相位。

线性调频干扰主要来自雷达，是一种频率随时间线性变化的信号。在时域上，随着时间的增加，谱线越来越密集，在频域上频谱图像则呈现出类似矩形窗的特点。其数学模型为：

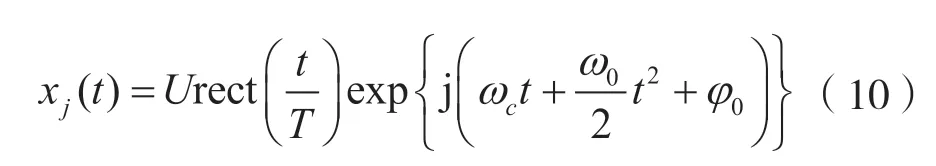
式中：U为幅度；ωc为载频；ω0为调制频率；T为脉冲宽度；rect 为矩形窗函数；φ0为初相且服从[0,2π)上的均匀分布。

宽带梳状干扰是在有用信号的频带内叠加k个窄带干扰，覆盖整个频带，主要来自人为设置的干扰机。宽带梳状干扰的数学模型为：

式中：k为调频干扰个数；Pk、ωk分别为每个正弦调频的功率和中心频率；∆ω为每个分量信号的带宽；α、β为每个信号的调制参数。

2 特征提取

本文使用的特征参数及其对应的符号和意义如表2 所示。采用Z-score 标准化法对x(t)进行预处理，使样本均值为0，方差为1，并提取表2 中的信号特征，得到信号特征向量X。

表2 特征参数

计算信号时域电平的一阶矩统计平均值α1：

式中：xi(t)为数据样本x(t)的第i个时域采样值；N为时域采样点数。

计算信号时域电平的二阶中心距α2：

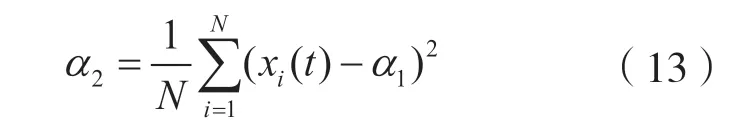
计算时域、频域和时频域三阶累积量的标准差α3，α9，α12：

计算时域、频域和时频域四阶累积量的标准差α4，α10，α13：

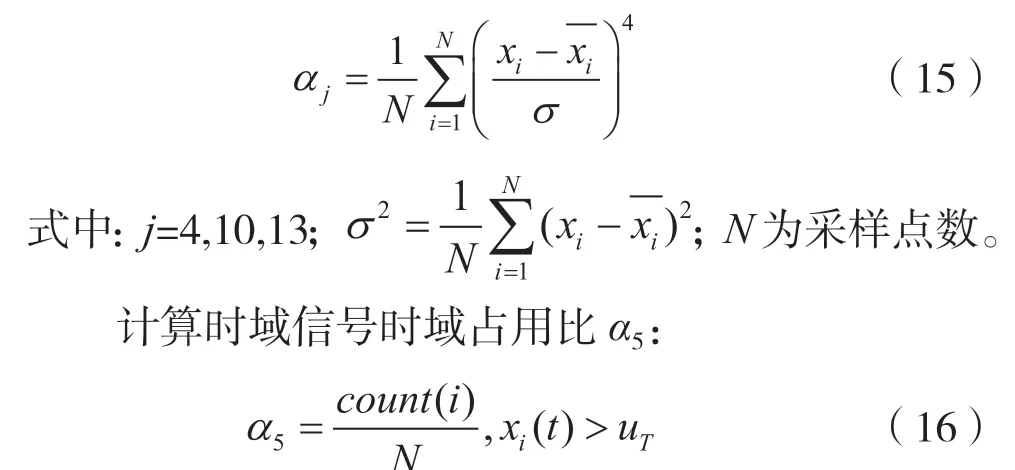
式中：count为计数函数；uT为时域阈值电平。

对时域信号进行傅里叶变换后得P(f)，估算频带占用度：

式中：fH为频带占用的最高频道；fL为频带占用的最低频道；Pg为频道占用阈值功率；∆f为频道总数。

计算功率谱动态范围α7：

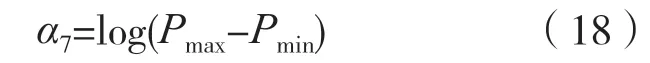
式中：Pmax为频谱最大幅值；Pmin为频谱最小非0幅值。

计算频谱冲击部分方差α8：

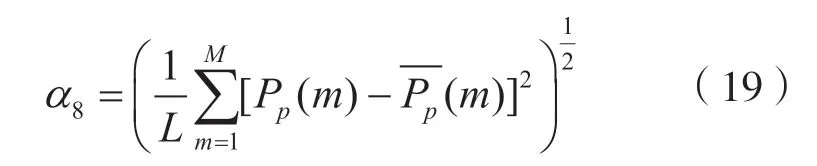
式中：L为滑动窗口长度；L=0.01M；M为频带宽度；Pp(m)为归一化频谱的冲激部分；为冲激部分的均值。Pp(m)的计算方式为：

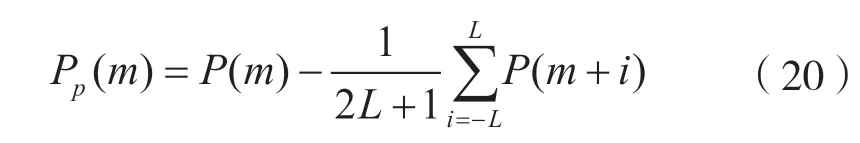
计算信号时频数据的谱熵α11：

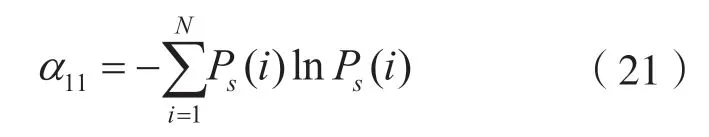
式中：Ps为xi(t)短时傅里叶变换后归一化的功率谱概率密度函数。

对X进行主成分分析（Principal Component Analysis，PCA）和降维。设原数据矩阵X的无偏样本协方差矩阵为Var[x]=E(XXT)，其中E[x]=0。对Var[x]特征分解后得到Var[x]=WΛWT，其中，Λ=diag(λ1,λ2,…,λn)。再 令Y=WTX=(y1,y2,…,yn)T，然后选取Λ中最大的k个特征值所对应的Y中的元素，组成维度更低的向量，WT即为转移矩阵。

3 基于深度学习的干扰识别

卷积神经网络（Convolutional Neural Network，CNN）是一种专门用于处理具有矩阵结构数据的神经网络，它通过逐层非线性变换实现复杂函数的逼近，能够有效提取深层次的数据特征[16-18]。把一个序列数据在时间轴上有规律地采样便能形成一维的网格，就能用卷积神经网络来进行处理。而长短期记忆网络（Long Short-Term Memory,LSTM）是一种时间循环神经网络，通过自循环来产生梯度长时间持续流动的路径作为初始长短期记忆，可以很好地解决循环神经网络（Recurrent Neural Network，RNN）存在的长期依赖问题。两种网络的联用，在处理序列分类问题上可能有更好的识别效果。于是，采用图1 所示的双层CNN+LSTM 网络模型进行训练。

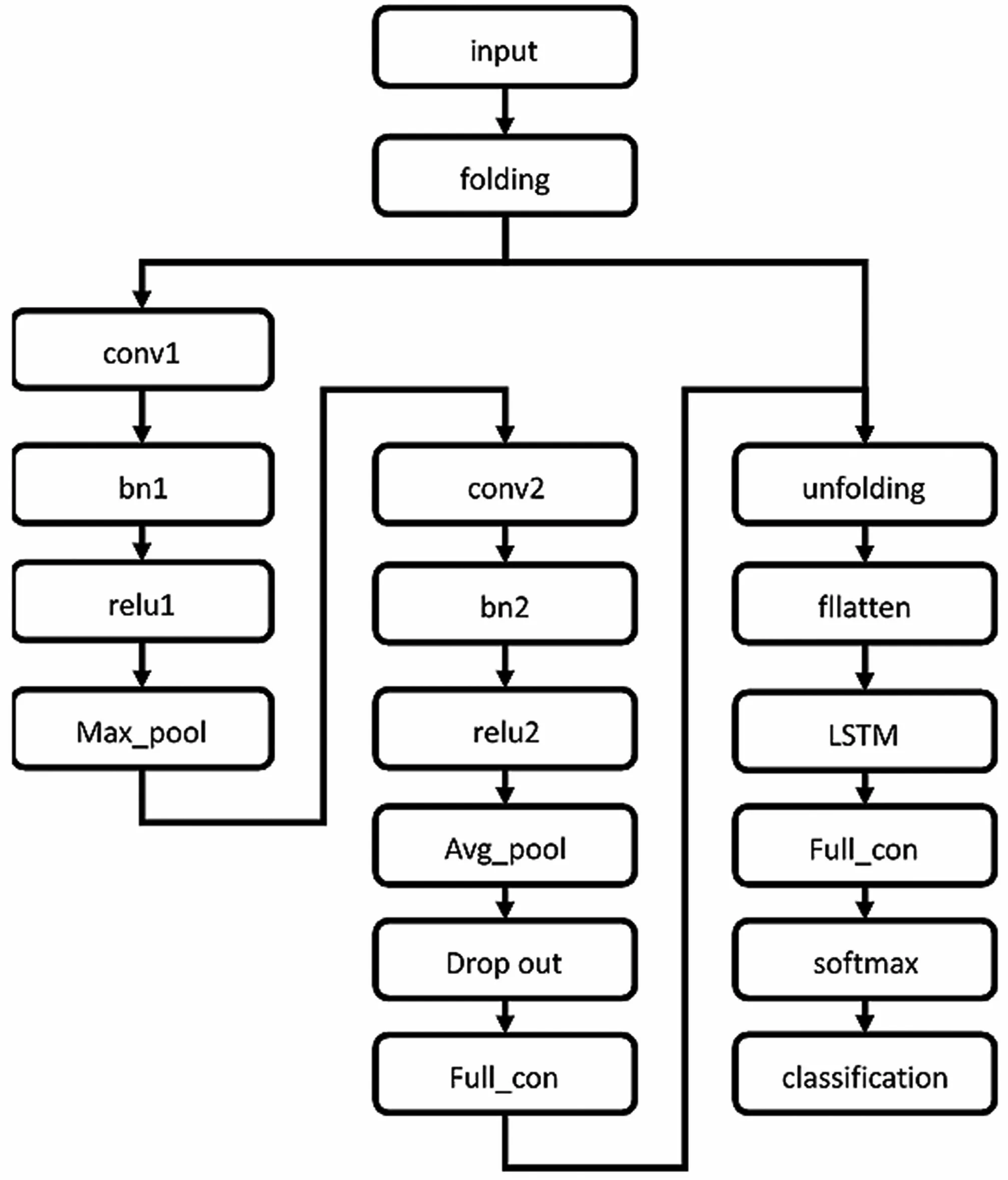
图1 深度学习网络模型

将信号特征矩阵Y输入双层卷积神经网络，采用线性整流函数作为卷积神经元激活函数，可得递推激活关系：

式中：f表示采用线性整流函数（Rectified Linear Unit，ReLU）作为神经元激活函数；w为传递权重；b为传递偏置；上标n表示神经元所在层数，n∈N*且n>1；下标i表示本层神经元序号；“·”表示输入信源；=Y。

为了减少隐层节点间的相互作用，达到缓解过拟合的作用，并达到正则化的效果，于是设随机因子ri～Bernouli(ρ)，则卷积层输出变为：

式中：ri是服从伯努利分布的随机因子，以ρ为概率随机生成只含0 和1的向量；“⊙”表示对应元素的相乘。

为避免超短波信道上干扰信号混叠造成弱信号特征不明显的情况，第一层卷积层采用最大池化，第二层卷积层采用平均池化。于是池化后的数据为：

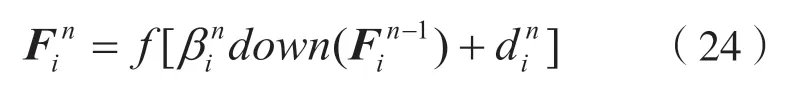
式中：f为ReLu 函数；β为权重；d为偏置；down表示下采样函数，含最大池化和平均池化函数。

通过flatten 层处理得到序列，再经LSTM网络，输出结果为：

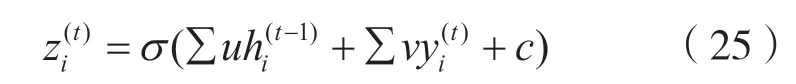
使用欧氏距离作为损失函数：

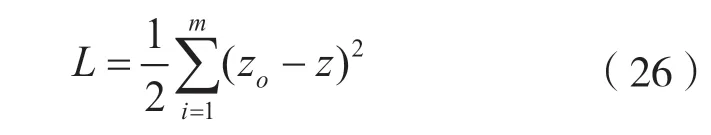
式中：zo为真实结果；z为识别结果；m为统计平均长度。

于是，可在损失函数最小的情况下用式（27）更新网络参数w，b，β，d，u，v，c，完成深度学习。

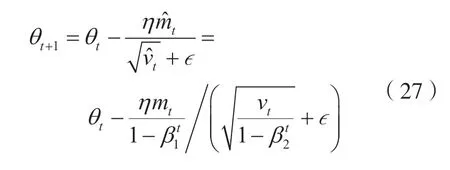
式中：mt为梯度的第一时刻平均值；vt为梯度的第二时刻非中心方差值；β1=0.9；β2=0.998 5；η为学习率；∊=10-8。

最后，利用准确率来描述识别结果准确性，由结果混淆矩阵M来计算：

式中：nij为M中的元素；k为类别数。

再用卡帕值（kappa）来反映识别结果的一致程度：

表3 卡帕值的意义

4 实验验证

使用MATLAB 2019b 进行软件模拟，并使用CA5000 接收机采集真实数据进行验证。信号采样时间均为1 ms，采样点1 024 个，采样率1.024 MHz，采集GPS 信号样本21 000 个，软件模拟干扰各3 000 个，按式（1）合成干扰叠加信号样本。选取70%的样本作为训练集，经反复实验，最小批量化长度设为256 个样本，具体参数如表4 所示时，实验收敛效果最佳，用时最少。

表4 网络参数表

4.1 强信号干扰的识别效果

为验证本文模型对大信号干扰和GPS 信号的识别效果，在干扰信号的功率超过GPS 地面用户接收信号50 dB 且尚未阻塞接收机的情况下，设置Uj=0，Us=1，即认为GPS 信号遭到完全压制，此时本文模型的干扰识别效果优于LSTM 网络模型。LSTM 网络与本文模型的训练效果对比如图2 和图3 所示。图2 给出了LSTM 网络的训练进度，准确率为0.817 5，均方误差为1.519 3，kappa为0.787 1；图3 给出了本文模型的训练进度，准确率为0.883 3，均方误差为1.291 0，kappa值为0.863 9。这说明强信号干扰GPS 信号时，本文模型具有明显的识别优势。

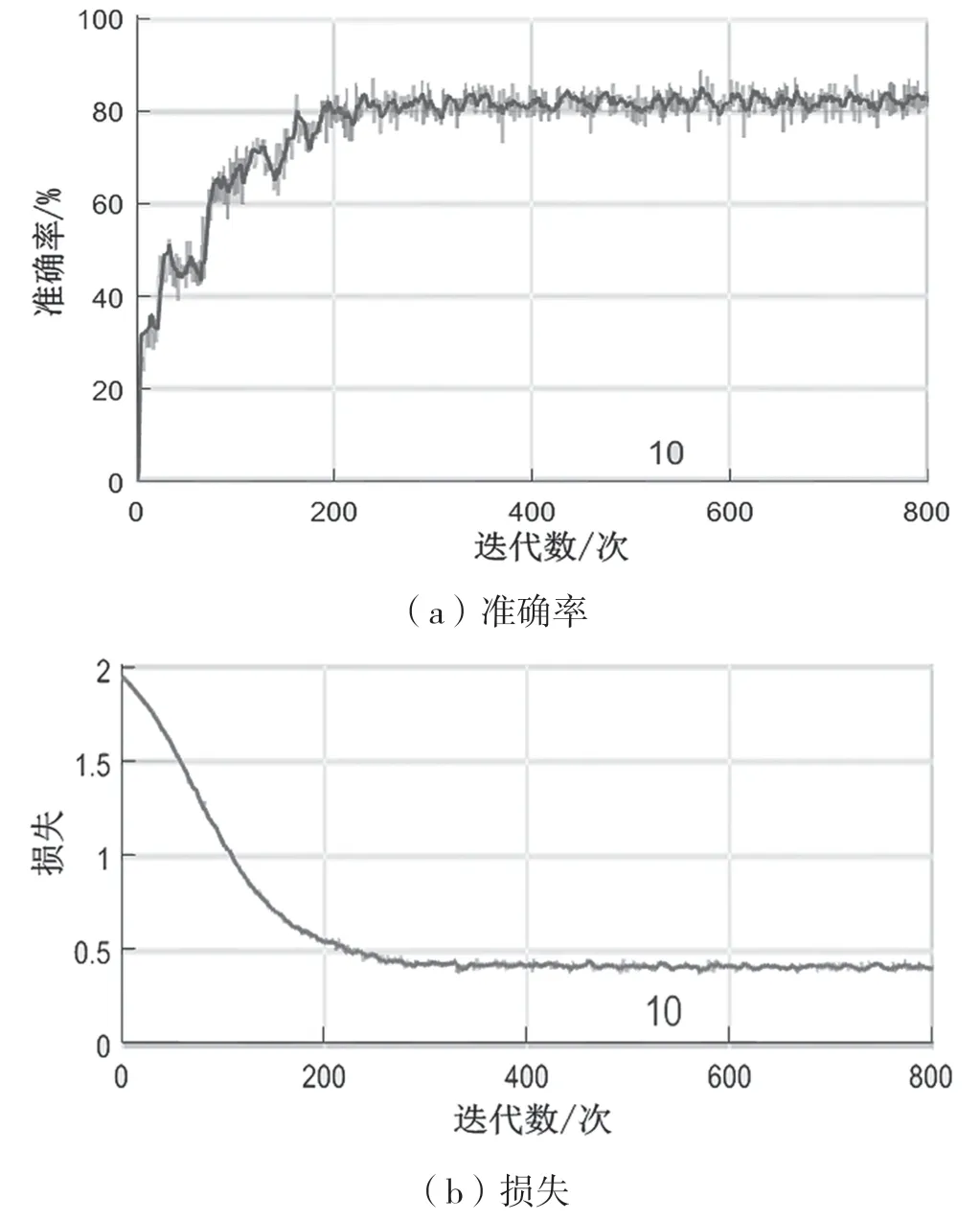
图2 LSTM 训练进度

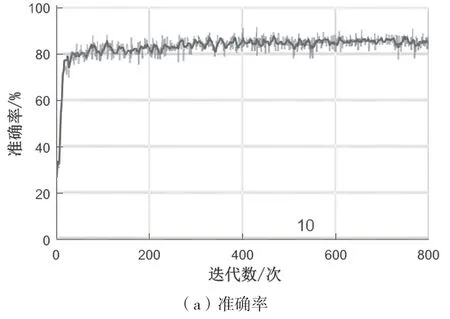
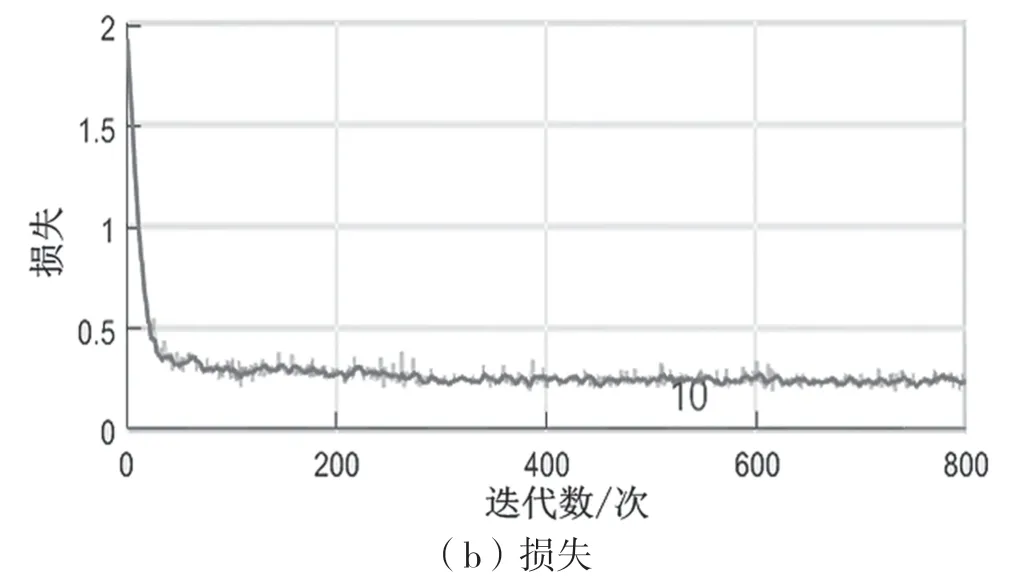
图3 本文模型训练进度

4.2 功率相近干扰的识别效果

为验证功率相近干扰的识别效果，设置干信比ε的范围为-3～3 dB（∈ [0.707,1.412]），此时本文模型的平均识别准确率为0.915 5，比LSTM 模型平均高出5.23%。图4 给出了不同干信比条件下两种模型识别准确率的对比情况，在所设干信比范围内，LSTM 模型识别准确率相近，而本文模型识别准确率随干信比一起提高，当干信比为2 dB 时，本文方法识别准确率为0.937 5，较LSTM 模型高7%左右。

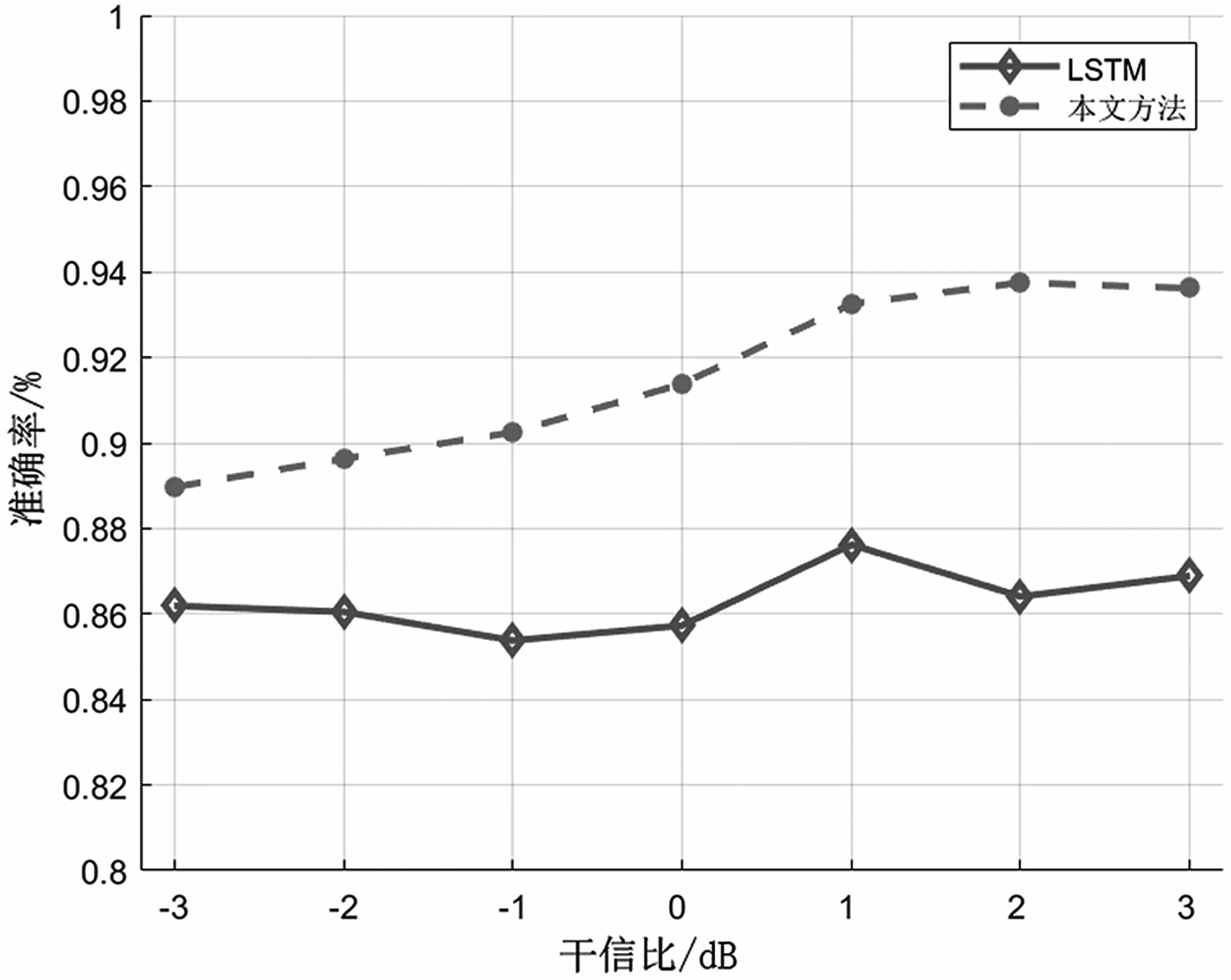
图4 本文模型与LSTM 模型的识别准确率比较

图5 给出了两种模型在识别误差方面的比较，本文模型的平均误差较小，且随着干信比的增大，本文模型的误差逐步降低。这说明当干扰信号的功率超过GPS 信号的功率1～3 dB 时，本文方法比LSTM 模型的识别误差更小。

图5 本文模型与LSTM 模型的均方根误差比较

表5 给出了LSTM 模型与真实分类对比的卡帕值为0.840 5，本文模型与真实分类对比的卡帕值为0.901 4，两种模型都达到了与真实分类几乎完全一致的程度，而且本文模型与LSTM 模型对比的卡帕值为0.895 5，说明两种模型的识别结果相近，但本文模型更接近于真实值。

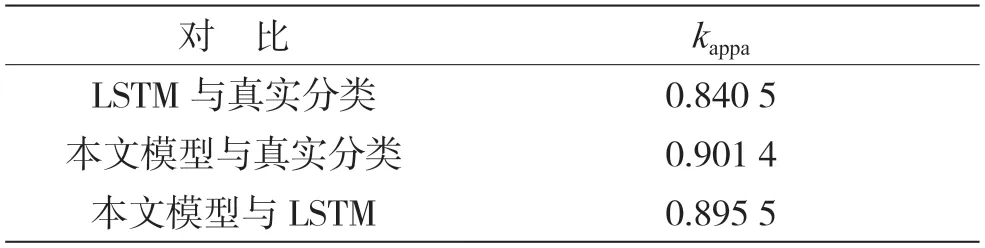
表5 识别结果一致性对比

图6 给出了不同干信比条件下两种模型识别结果与真实结果之间的卡帕值比较，随着干信比的提高，本文模型识别结果的一致性逐渐增加，而LSTM 模型则几乎没有变化，这是导致两种模型识别差异的主要因素，同时也说明当干扰信号的功率超过GPS 信号的功率1～3 dB 时，本文方法的识别结果均较高。

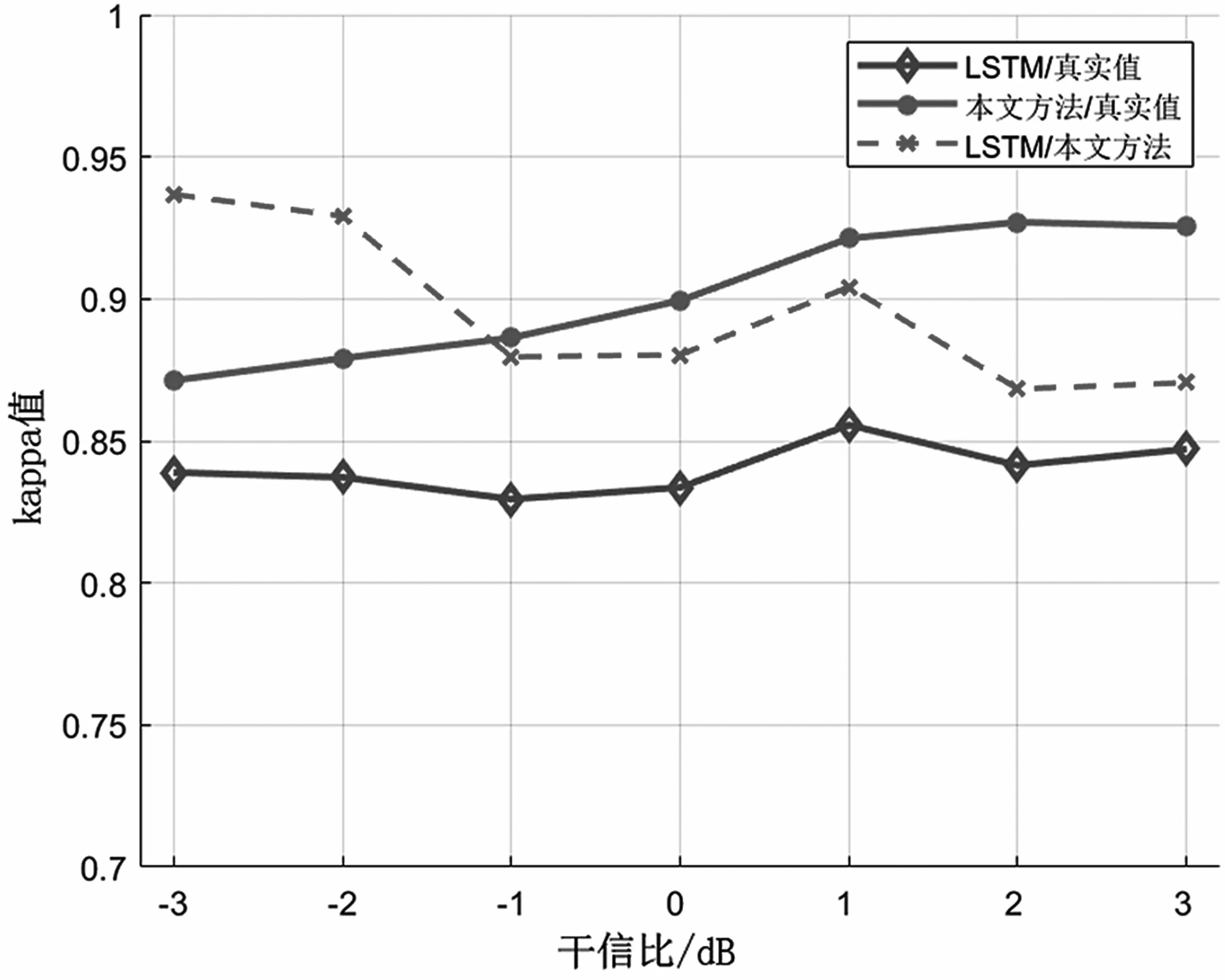
图6 识别结果一致性对比

图7 给出了干信比为2 dB 时两种模型识别结果与真实分类之间的混淆矩阵，由于窄带高斯噪声与宽带高斯噪声的分布相似，在样本数据有限的情况下，容易造成误判。但是，本文模型的误判比例比LSTM 模型的误判比例低。

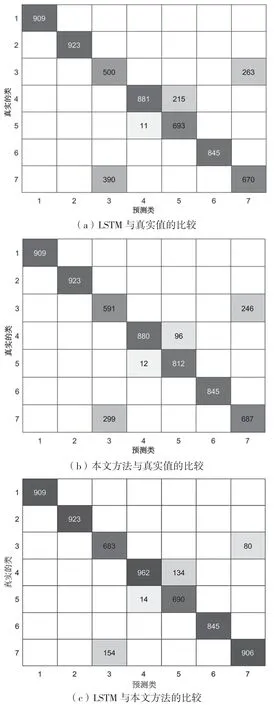
图7 识别结果混淆矩阵

图8、图9 分别给出了两种模型在干信比为2 dB时的训练进度。显然，本文模型在网络训练过程中损失下降明显，收敛速度快，平均准确率更高。

图8 干信比2 dB 时，LSTM的训练进度

图9 干信比2 dB 时，本文模型的训练进度

综上，本文模型可以有效识别功率强于GPS 信号的无线电干扰，对于干信比为-3～3 dB的干扰信号也有较好的识别效果，且具备一定的抗噪声和抗混叠干扰的能力。另外，在一致性相近的前提下，较传统LSTM 模型具有更高的识别准确率。

5 结语

本文面向无线电监测工作需求，根据实际干扰情形研究了GPS 干扰模型，并选取合适特征参数作为干扰信号的识别依据，构建了“双层CNN+LSTM”的深度学习网络模型。该模型通过特征提取和分类识别，达到由无线电监测数据区分GPS 干扰的目的，有助于缩小目标干扰源的排查范围，提高工作效率。实验结果表明，本文所述方法能够有效识别带限高斯噪声、宽带均匀噪声、噪声调幅、单频脉冲、线性调频等典型GPS 干扰，识别结果与真实值几乎一致。在强信号干扰时，干扰识别的准确率为0.883 3，对于干信比为-3～3 dB的干扰信号也有较好的识别效果，平均识别准确率为0.915 5，具备一定的抗噪声和抗混叠干扰的能力，说明本文方法在功率相近的干扰识别方面有一定的优势。但是，本文的研究仍具有局限性，提取的信号特征数量与样本类型的种类有关，且不同特征参数对于分类识别的贡献程度是不同的，仍需继续深入研究。另外，对于有监督的深度学习，尚不能遍历可能的干扰类型，对于未知类别，仍需更多真实、可靠的样本数据作为训练集的有效补充，以丰富数据集，提高准确率。下一步将在兼顾深度学习的网络训练速度和保证识别准确率的前提下，深入研究GPS 干扰信号的特征提取方法，优化网络结构。