谈谈阿氏圆的几个性质及其应用
2022-04-09刘美玲
刘美玲
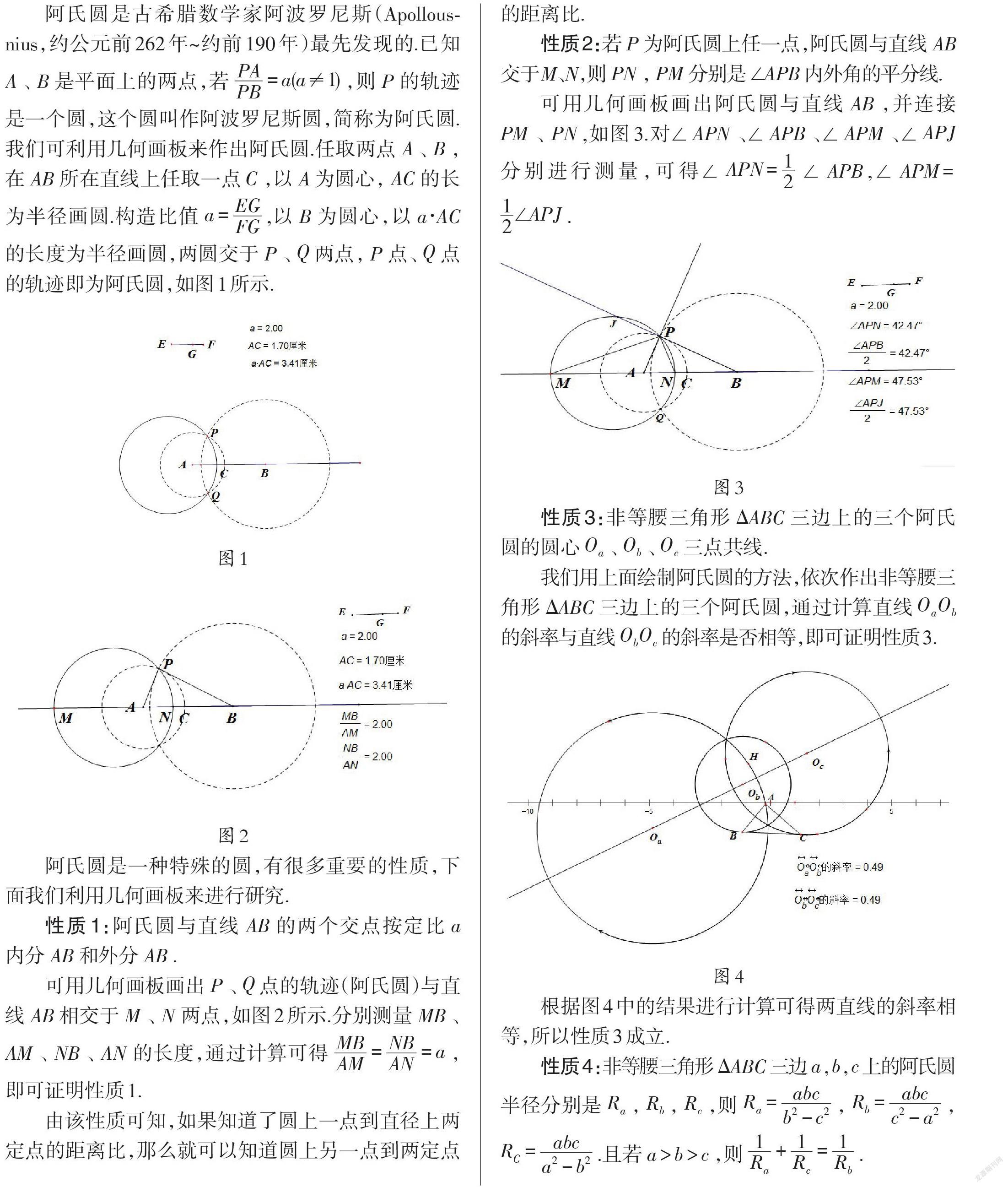

阿氏圆是古希腊数学家阿波罗尼斯(Apollous⁃ nius,约公元前262年~约前190年)最先发现的.已知A、B 是平面上的两点,若 =a(a ≠1),则 P 的轨迹是一个圆,这个圆叫作阿波罗尼斯圆,简称为阿氏圆.我们可利用几何画板来作出阿氏圆.任取两点 A、B,在 AB 所在直线上任取一点 C,以 A 为圆心,AC 的长为半径画圆.构造比值 a = ,以 B 为圆心,以 a ∙AC的长度为半径画圆,两圆交于 P、Q 两点,P 点、Q 点的轨迹即为阿氏圆,如图1所示.
阿氏圆是一种特殊的圆,有很多重要的性质,下面我们利用几何画板来进行研究.
性质1:阿氏圆与直线 AB 的两个交点按定比a 内分 AB 和外分 AB .
可用几何画板画出 P、Q 点的轨迹(阿氏圆)与直线 AB 相交于 M、N 两点,如图2所示.分别测量 MB 、 AM、NB、AN 的长度,通过计算可得= =a ,即可证明性质1.
由该性質可知,如果知道了圆上一点到直径上两定点的距离比,那么就可以知道圆上另一点到两定点的距离比.
性质2:若 P 为阿氏圆上任一点,阿氏圆与直线 AB 交于M、N,则 PN,PM 分别是∠APB 内外角的平分线.
可用几何画板画出阿氏圆与直线 AB,并连接 PM 、PN ,如图3.对∠ APN、∠ APB、∠ APM、∠ APJ 分别进行测量,可得∠ APN = ∠ APB , ∠ APM =∠APJ .
性质3:非等腰三角形ΔABC 三边上的三个阿氏圆的圆心 Oa、Ob、Oc三点共线.
我们用上面绘制阿氏圆的方法,依次作出非等腰三角形ΔABC 三边上的三个阿氏圆,通过计算直线OaOb的斜率与直线ObOc的斜率是否相等,即可证明性质3.
根据图4中的结果进行计算可得两直线的斜率相等,所以性质3成立.
性质4:非等腰三角形ΔABC三边 a ,b ,c 上的阿氏圆半径分别是 Ra ,Rb ,Rc,则 Ra = abcRb = abcRC= .且若 a >b >c,则+ = .
可以在图4的基础之上作图,因为圆 Oa、圆 Ob 、圆Oc分别经过A、B、C三点,分别测出OaA、ObB、OcCabcabc的长度,即为 Ra , Rb ,Rc .再量出a2-b2,建立等式关系即可.
由图5中的数据,可得+ = + = = ,说明上述性质是成立的.
利用几何画板的作图、测量功能,可以轻松作出阿氏圆,计算出结果,证明上述性质成立.在解题时,灵活运用阿氏圆的性质,能快速找到解题的思路,使问题顺利得解.
例1.已知抛物线 C : y2= 8x 的焦点为 F ,准线与x 轴的交点为 K,点 A 在 C 上,且AK = AF ,Δ AFK 的面积为().
A.4 B.8 C.16 D.32
分析:本题直接求解较为困难,不妨采用数形结合法,根据题意画出图形,问题的本质就会自然而然地呈现在我们面前.首先建立直角坐标系,绘出抛物线C 的图象以及 F 、K 点的位置,如图6.设 A(x,y),由题目条件AK = AF ,可得 A 是阿氏圆与抛物线 C 的交点,求得阿氏圆轨迹方程为:= ,化简得 x2+y2- 12x +4=0,则阿氏圆与 y2= 8x 交点为 A(2,±4),所以 SΔAFK = FK ∙yA=8 ,故答案选B项.
解答本题主要运用了阿氏圆的定义,根据其定义建立关系式,求得 K 点的轨迹方程,通过分析图象确定 A点的位置,再根据三角形的面积公式求得问题的答案.
例2.在平面直角坐标系xOy中,点 A(0,3),直线 l:y =2x -4,设圆C 的半径为1,圆心在 l 上.若圆C 上存在点M,使MA =2MO,求圆心C 的横坐标 a 的取值范围.
分析:由 MA =2MO 可以判断,点 M 是阿氏圆上的点.求得阿氏圆的轨迹方程为: x2+(y +1)2=4.而圆 C 是圆心在直线 l 上,半径为1的圆.绘制如图7所示的图形,因为 M 也在圆 C 上,所以 M 即为圆 C 与阿氏圆的交点,由图8可知圆C 的圆心在 O1、O2之间运动.设圆 C的圆心坐标为( x ,2x -4),则1≤ ≤3,即 0≤ x ≤ .
解答本题主要运用了阿氏圆的定义以及性质3、性质4.首先根据题意确定 M 点为阿氏圆上的点,得到M 点的轨迹方程,然后利用阿氏圆的性质3、性质4确定圆心 C 的横坐标的取值范围.
总之,当遇到有关两点一圆的问题、动点到两定点的距离之比等于定比的问题时,可以利用阿氏圆的定义或性质将问题进行巧妙地转化,这样有助于提升解题的效率.
(作者单位:湖北省武汉市光谷实验中学)
