仿生非光滑沟槽轮胎抗滑水性能研究*
2022-04-08刘从臻孙运芬李永强徐成伟谢孟雨
刘从臻 孙运芬 李永强 徐成伟 谢孟雨
(山东理工大学,淄博 255000)
主题词:轮胎花纹沟 仿生非光滑沟槽 减阻机理 边界层 动水压力
1 前言
轮胎滑水是交通事故的五大诱因之一。车辆在积水路面的行驶速度一旦超过临界速度,轮胎接地区域内积水无法及时从花纹沟内排出,导致发生滑水现象,严重威胁行车安全。如何有效提高轮胎抗滑水性能是轮胎研究领域面临的一个重要问题。
为提高轮胎抗滑水性能,国内外众多学者进行了大量的模拟和试验研究。B.Wies、Gilbert 和Jeng 等通过试验探究了花纹结构对轮胎抗滑水性能的影响,结果表明,适当增大花纹沟体积可以改善轮胎抗滑水性能;臧孟炎、Kumar 等对比分析了混合、纵向和光面轮胎的抗滑水性能,结果表明,增加花纹沟数量和宽度可以增强轮胎排水能力,提高抗滑水性能。花纹沟的结构形式是提高轮胎抗滑水性能的关键,但随着花纹沟体积占比的增大,轮胎其他性能将会受到影响。如何在不影响其他性能的前提下提高轮胎抗滑水性能是值得进一步研究的课题。
近年来,仿生技术已成功解决了工程应用中的许多难题。Walsh 等研究发现鲨鱼皮表面具有顺流向的沟槽,并将沟槽结构应用于航天器,使其阻力减少了5.6%。德国Bechert 等通过模拟鲨鱼表面三维肋条结构进行风洞试验,发现三维肋条表面可以产生显著的减阻效果,与光滑平板相比,湍流剪应力降低了7.3%。李慧明等发现,横向海豚表面棱纹沟槽对层流和湍流均具有减阻作用。
仿生减阻技术为提高轮胎抗滑水能力提供了新思路。本文基于仿生非光滑结构对流体的减黏降阻的特性,以鲨鱼皮表面沟槽作为仿生对象,建立3 种微结构沟槽,分析其对水流阻力的影响,并将最优结构布置于复杂花纹轮胎沟底,以期在不影响其他性能的前提下提高轮胎抗滑水性能。
2 轮胎有限元模型建立与验证
2.1 模型建立
以185/60 R15 子午线轮胎为例,其额定气压为250 kPa,额定载荷为3 920 N。利用ANSYS Workbench建立轮胎模型,该模型由胎面、胎侧和轮辋3 个部分组成。轮胎与路面均为壳体模型,其中胎面和胎侧为均匀正交各向异性弹性材料,路面和轮辋为刚性体,如图1a所示,材料参数如表1所示。

表1 轮胎材料参数

图1 有限元模型
轮胎在积水路面上行驶时,流体覆盖整个路面,若按轮胎实际滚过的路径进行仿真分析,计算量巨大,不易实现。为分析轮胎滑水过程中的流体状态,同时提高计算效率,需约束轮胎沿路面的运动方向,并对水流施加一定的速度,使其与轮胎相对运动,通过Hyper⁃Mesh 软件将轮胎壳体模型转化成实体,并进行“布尔减”操作得到流体域,利用单向流固耦合对其进行仿真分析。经过实际分析,确定流体域模型长为200 mm、宽为200 mm、高为10 mm。在Fluent 中对流体域进行独立分片四面体网格划分,共产生网格单元364 505 个,节点76 043个,如图1b所示。
2.2 流体域边界条件设置
流体域的材料属性均设置为水,为了保证水流不渗透至轮胎内部,需在该区域定义边界条件。在Fluent软件中设置流体域的边界条件,如图2所示。

图2 轮胎滑水边界条件
速度入口:将流体域的入口设为速度入口,水流分别以70 km/h、80 km/h、90 km/h和100 km/h的速度流动。
压力出口:流体域的出口和两侧设为压力出口,并设定相对参考压力点的流体静压为101.325 kPa。
壁面:将底面设为无剪切力的滑移壁面,其移动速度与水流速度相同。
耦合面:将流体域接触面设为轮胎与水层的力学信息传递面。
轮胎滑水仿真分析过程中,设定水流为等温、不可压缩的粘性流体,控制方程组为纳维-斯托克斯(N-S)方程,湍流模型选用Realizable-,壁面函数设为标准壁面函数,采用Smoothing 和Remeshing 动网格技术处理网格变形问题,流场的数值求解方法选用SIMPLE格式。
2.3 模型验证
在研究轮胎的滑水性能时,胎面变形对于轮胎排水至关重要。为验证有限元模型的精度与可靠性,采用型号为CSS-88100 的电子万能试验机进行加载试验,如图3所示。测试方法及试验步骤如下:

图3 静态加载试验
a.为排除温度对胎压的影响,试验前、后保持室内环境温度为25 ℃。
b.在待测轮胎的胎侧均匀布置6 个测试样点,取不同位置径向变形的平均值,以确保试验结果的准确性。
c.分别设定轮胎胎压为240 kPa、340 kPa,并在室温环境下静置24 h。
d.准备复写纸和A4 白纸,放置于加载试验台表面,用于收集每次加载时轮胎接地印迹。
e.将静置后的轮胎安装到试验机上,利用激光水平仪将轮胎调至水平位置,在其左侧放置钢尺并加以固定,记录轮胎的初始半径。
f.利用计算机终端控制加载速度,对不同胎压下各测试样点进行加载,载荷分别为4 kN、6 kN、8 kN、10 kN,加载完成后持压1~2 min,记录试验数据,共48组。
g.将同一胎压、载荷下6 个样点的径向变形值进行整理,去除最大值和最小值,对剩下的4 组数据取平均,完成载荷-径向变形曲线绘制,并将每次加载后带有轮胎印痕的纸张取出进行轮廓扫描。
静态加载时,不同气压下“载荷-径向变形”结果如图4 所示,载荷与径向变形近似呈线性关系且误差在5.3%以内,说明有限元模型精度较高。
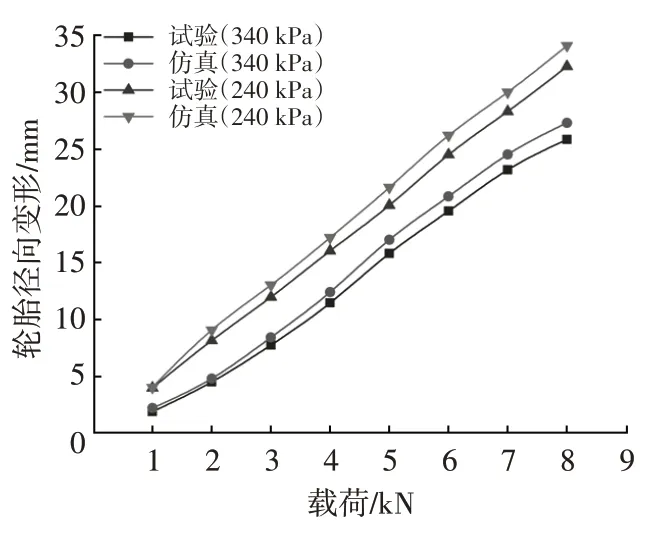
图4 载荷-径向变形曲线
轮胎静态接地印迹对比如图5所示,所获印痕形状近似,且接地压力分布情况一致性良好。试验与仿真所得的几何参数对比结果如表2 所示。试验与仿真最大误差为3.17%,表明其精准性高。“载荷-径向变形”和接地印迹对比均证明了模型的可靠性,可以用于进一步仿真分析。
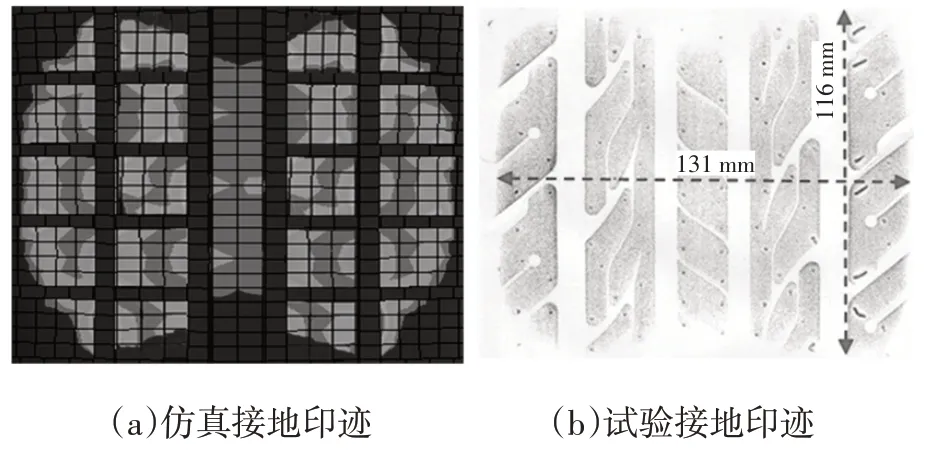
图5 轮胎静态接地印迹对比

表2 轮胎接地印迹几何参数试验与仿真结果
3 仿生非光滑表面花纹沟数值分析
3.1 仿生花纹沟模型建立
选取鲨鱼皮表面鳞盾沟槽为研究对象,利用ANSYS 软件对纵向花纹沟进行几何建模(深8 mm、长30 mm、宽7 mm),将3种仿生微结构沟槽分别布置于花纹沟底,其结构形式如图6所示。为确保微结构沟槽能对边界层内部结构产生影响,沟槽尺寸不宜过于靠近边界层上边界。以流体边界层厚度理论为依据,对微结构沟槽的尺寸进行估算,边界层厚度为:
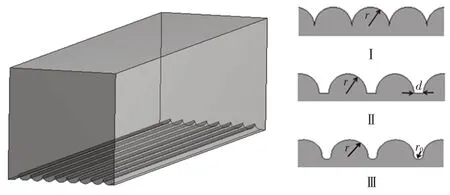
图6 仿生花纹沟模型

式中,为特征长度;为雷诺数。
经计算,花纹沟内流体的最大边界层厚度约为0.91 mm。故将3种沟槽中的凹槽半径设置为0.40 mm,沟槽Ⅱ的间隔=0.20 mm,沟槽Ⅲ的间隔圆弧半径=0.10 mm。
3.2 网格划分及求解设置
为了捕捉到近壁区的水流运动特征,将其进行网格细化,第1层的网格厚度与(第1层网格至壁面的无量纲距离)取值有关。边界层中粘性底层的无量纲厚度约为0≤≤5,因此在计算靠近壁面的第1层网格厚度时,为捕捉到流体特征,要保证≤5。近壁面的第1层网格厚度为:

式中,为流体的动态粘度;C为经验常数,通常取C=0.09;κ为第1 节点的湍动能。
经过反复尝试得出,第1层的网格厚度为0.01 mm,增长率为1.20,计算域最大网格尺寸为0.25 mm,如图7所示。此外,对花纹沟模型进行仿真分析时,除湍流模型选用Standard-模型,其他设置均与轮胎流体域一致。

图7 仿生沟槽局部网格示意
3.3 轮胎花纹沟流动特性分析
动水压力是水在流动时管道某一点的总压力与速度压力之差,简称动压,可由伯努利方程获得。在流体域中,不可压缩流体在不同截面处的伯努利方程为:

其中,

式中,、分别为2 个截面处的压强;、分别为2个截面上的平均速度;、分别为2 个截面处的高度;=1 000 kg/m为水流密度;为重力加速度,可取9.8 m/s。
当不可压缩流体水平流动时,伯努利方程可进一步简化为:

式中,为水压;为来流速度;为常量。
由式(4)可知,速度的消耗转换为动压,即动压越高,水流阻力越大。通过仿真分析得到不同来流速度下仿生花纹沟的动水压力,如表3所示。
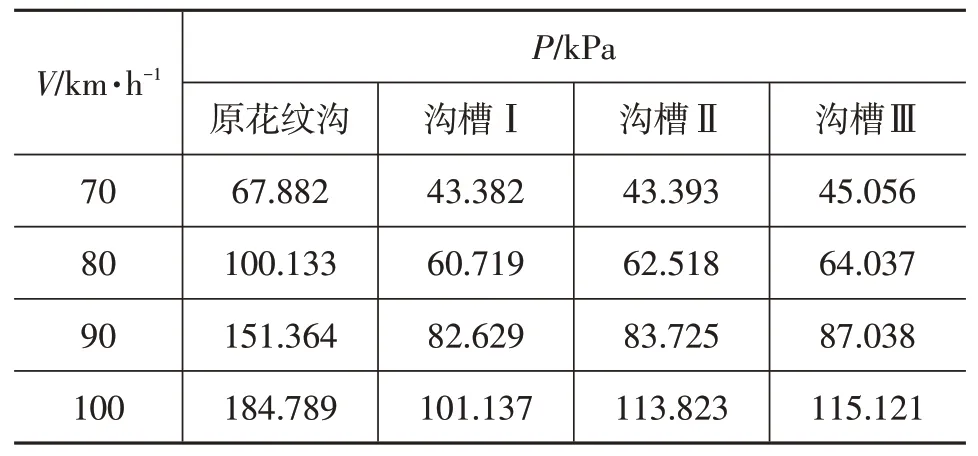
表3 不同来流速度下各仿生花纹沟动水压力
由表3可知,随着来流速度的增加,4种花纹沟槽内的动水压力均随之增加。在相同来流速度下,3种仿生花纹沟的动水压力均小于原花纹沟,其中沟槽I的动水压力最小。结果表明:非光滑沟槽可降低水流阻力,减小动水压力。
为探究非光滑沟槽对花纹沟的减阻效果,以减阻率为试验指标进行分析:

式中,、分别为原花纹沟与仿生花纹沟的剪切应力。
>0 表示非光滑沟槽具有减阻效果,且其值越大,减阻效果越明显;<0 表示非光滑沟槽具有增阻特性,绝对值越大,增阻效果越明显;=0 表示非光滑沟槽无作用。各花纹沟模型在不同来流速度下的减阻效果如表4 所示。结果表明,3 种非光滑沟槽都具有减阻的效果,且随着来流速度的增加,减阻率先升高后降低。通过对比分析发现,沟槽I的减阻效率优于其他2种,减阻效果最好,其中沟槽III的减阻效果最差,其结果与动水压力分析一致。
表4 各花纹沟模型减阻率
4 非光滑沟槽减阻机理分析
由减阻率分析可知,在所研究的来流速度中,90 km/h 时各沟槽减阻效果最好。以此速度为例,通过对各花纹沟的剪切应力云图、速度云图、速度矢量进行分析,探索不同非光滑沟槽结构的减阻机理。
4.1 剪切应力分析
壁面剪切应力的大小可以反映流体的粘性阻力。各花纹沟剪切应力云图对比结果如图8所示。由图8可知,仿生花纹沟的入口应力比原始花纹沟大,但随着流体的不断流入,其剪切应力逐渐减小,位于中后区域的剪切应力远小于原花纹沟,最终实现减阻。对仿生花纹沟的入口剪切应力和低剪切应力所占区域进行比较,沟槽Ⅰ的壁面应力明显小于其他2 种沟槽。对比分析表明:3 种沟槽都能减小水流的粘性阻力,且槽Ⅰ的减粘效果最好。

图8 剪切应力对比
4.2 速度分析
为了避免入口和出口效应的影响,选择距离入口15 mm 处的横截面流向速度云图进行分析,如图9 所示。显然,光滑的原花纹沟速度场与仿生花纹沟相比有明显区别。原花纹沟的边界层很薄,速度在边界层内便达到了主流速度,其速度梯度较大且变化剧烈,摩擦阻力最大。仿生花纹沟因非光滑沟槽的存在,壁面边界层厚度增加,边界层内的缓冲层和对数律层均随之相应向上移动,到达主流速度的距离增加,可减小粘性底层速度梯度,降低摩擦阻力,提高主流速度。对比可知,沟槽Ⅰ的边界层厚度高且均匀,主流速度最大,减阻效果最好。


图9 距入口15 mm处特征平面速度分布
4.3 速度矢量分析
花纹沟的纵截面速度矢量如图10 所示。仿生花纹沟底部有大量的低速流体,流动较为平缓,流速较高的流体均位于沟槽上方,难以对花纹沟底部进行扫掠,剪切应力小。随着流体的流入,低速流体的厚度逐渐增加,其上方流体的流速变大,加快了花纹沟的排水速度。其次,观察壁面的速度矢量图可以发现,由于非光滑沟槽的存在,速度矢量能够限制在沟槽范围内,且大多顺流向呈直线分布,相比原花纹沟减少了流体横向移动,提高能量效率,达到减阻的效果,如图11 所示。

图10 纵截面速度矢量
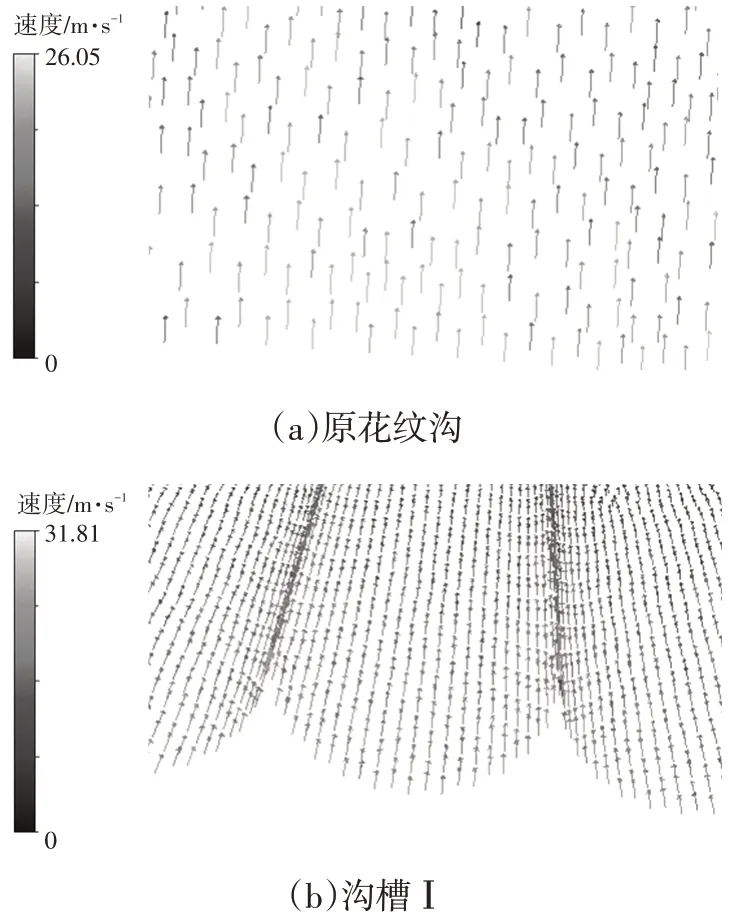

图11 壁面速度矢量
5 仿生轮胎滑水分析
为分析非光滑结构在复杂花纹轮胎上应用的有效性,将减阻效果最优的沟槽Ⅰ布置于轮胎纵向花纹沟底部,并与原轮胎进行滑水分析对比,其模型如图12 所示。由于微结构沟槽的存在,仿生轮胎流体域网格需进行局部加密处理,共产生网格单元1 574 778 个,节点304 500个。整体网格划分方法、湍流模型、边界条件等设置均与原轮胎一致。

图12 仿生模型
表5给出了不同水流速度下作用在2种轮胎胎面的平均动水压力。由表5可知,仿生轮胎胎面受到的动水压力均小于原胎,且速度越高,胎面动水压力下降趋势越明显。当速度为90 km/h 时,原胎面动水压力大于充气压力,仿生胎面平均动水压力小于充气压力,这说明此速度下的原胎发生滑水,而仿生胎还未达到滑水速度,添加仿生结构后的滑水速度得到提高。

表5 不同水流速度下不同方案胎面动水压力
为方便观察轮胎各处流场变化,提取高于路面4 mm 处,水流速度为90 km/h时的云图进行分析。流体的动压可以作为轮胎抗滑水性能的评价指标。原胎与仿生胎动水压力云图如图13所示。轮胎在积水路面行驶时,由于楔形区域的存在,胎面中央的动水压力较胎侧大。相比于原胎(动水压力峰值1 460 kPa),添加了非光滑沟槽的仿生胎(动水压力峰值1 310 kPa)动水压力降低约11.45%。其原因在于,沟槽的存在降低了水的滞留,使沟槽前方区域的动水压力明显降低,提高了轮胎抗滑水性能。
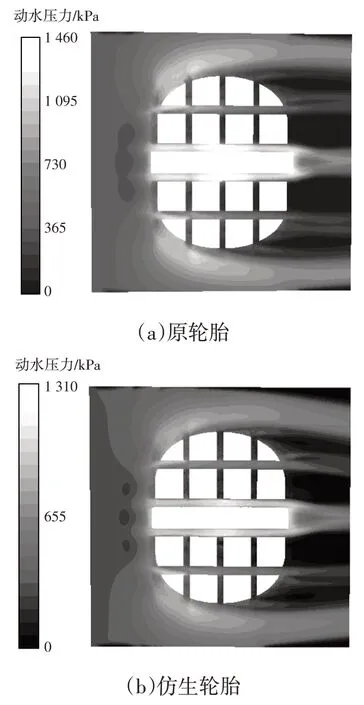
图13 不同方案动水压力云图
图14所示为原轮胎与仿生轮胎的速度云图。轮胎花纹沟的排水能力对轮胎抗滑水性能影响显著。当水的来流速度相同时,轮胎花纹沟内水流速度越快,其排水能力越强。由图14 可知,复杂花纹轮胎的中央纵向花纹沟起主要排水作用,对其增设非光滑仿生沟槽后,最大水流速度提高约7.48%,且高流速区域明显增大,排水能力增强,从而提高了轮胎滑水临界速度。

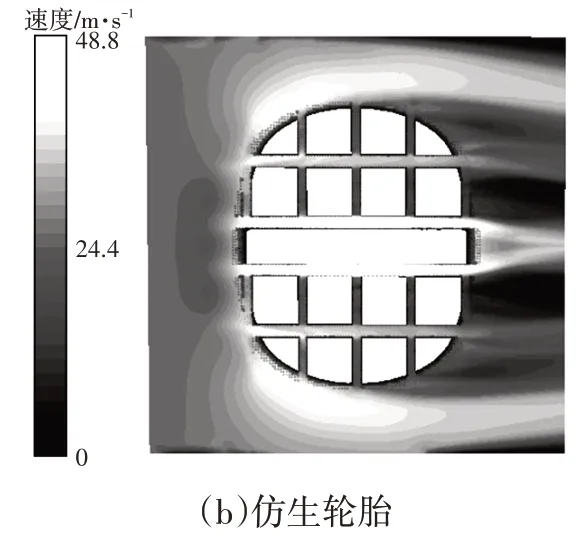
图14 不同方案速度云图
6 结论
a.本文构建的3 种仿生非光滑沟槽均具有减小水流阻力、降低动水压力的作用,且随着来流速度的增加,减阻效果先增加后降低,在所测速度中90 km/h 效果最佳。
b.仿生非光滑沟槽的存在可以影响边界层的分层结构,增加壁面边界层厚度,减小粘性底层速度梯度,有效降低水流阻力,提高花纹沟主流速度,增大花纹沟排水量。
c.3 种仿生沟槽中,顶部具有尖峰结构的沟槽Ⅰ减阻效果最好,将其应用于复杂花纹轮胎,对比分析发现,仿生轮胎排水能力较好,能够减少水的滞留,并在不改变轮胎其他性能前提下提高轮胎抗滑水性能,保障了湿滑路面的行车安全性。
