基于非线性预测和沿轨迹线性化MPC的车辆路径跟踪控制方法*
2022-04-08张睿谢正超赵晶王百键
张睿 谢正超 赵晶 王百键
(1.华南理工大学,广州 510641;2.澳门大学,澳门 999078)
主题词:路径跟踪 模型预测控制 直接横摆力矩控制 制动力分配
1 前言
先进驾驶辅助系统和自动驾驶系统的应用可以显著提高车辆的安全性和操作便利性,而精确的路径跟踪控制技术是其实现的必要条件。经典的纯跟踪法(Pure Pursuit)是基于车辆运动学模型开发的,适用于运动速度和加速度较低的工况。以车辆动力学模型为基础,结合线性二次型调节器(Linear Quadratic Regulator,LQR)能够适应车辆的高速高动态工况,引入和改进预瞄策略可以进一步减小跟踪误差。模型预测控制(Model Predictive Control,MPC)在多模型约束处理方面的优势使其能够较好地与智能汽车的感知、规划和控制环节相结合,并且具有更好的控制效果。Falcone 等开发了模型预测主动前轮转向控制系统,结合制动力分配实现了车辆的运动稳定性控制,其采用的线性时变模型预测控制(Linear Time-Varying Model Predictive Control,LTV MPC)算法具有较好的实时性。
然而,在路面湿滑、紧急避险或高速过弯等情况下轮胎侧偏力可能趋近饱和,此时车辆动力学具有显著的非线性特点,在每个控制周期以当前工作点的线性化模型作为整个预测时域内的近似模型会引起较大的预测误差,而目前尚无算法可保证在较短的控制周期内求出非线性优化问题的全局最优解,直接采用非线性预测模型不能保证实时性。
为改善路径跟踪控制效果并尽量减少在线计算量,本文基于非线性预测和沿轨迹线性化的模型预测控制算法(Model Predictive Control algorithm with Nonlinear Prediction and Linearization along the Trajectory,MPC-NPLT)设计车辆路径跟踪控制器,根据大轮胎侧偏角工况下的控制需求制定直接横摆力矩控制(Direct Yaw-moment Control,DYC)系统的切换策略和制动力分配策略,以实现其与转向系统的协调控制,并在MATLAB/Simulink平台搭建控制器,联合CarSim 仿真验证该算法的有效性。
2 车辆动力学模型
预测控制是基于模型的控制算法,预测模型应在一定程度上反映控制对象的动态特性,并在此基础上具有尽量低的阶数以减少在线计算量。路径跟踪问题的核心是控制车辆跟踪参考路径运动,关注车辆是否按照预定的航向角行驶,以及实际位置与参考路径的偏差。为简化模型,假设车辆在平坦的路面上行驶,忽略车辆的垂向运动和悬架的作用,俯仰角和侧倾角均为零,忽略阿克曼转向几何,2个前轮转向角一致且与转向盘转角为线性对应关系。
定义为固联于地面的坐标系,假设其为惯性系。定义为车辆固联坐标系,原点为车辆的质心。建立车辆动力学模型如图1 所示,其中、分别为质心到前、后轴的距离,为轮距,为车轮半径,为整车质量,I为车辆绕轴的转动惯量,为航向角,即轴与车辆轴之间的夹角,v为纵向速度分量,v为侧向速度分量,为横摆角速度,为前轮转向角,、分别为前、后轮的侧偏角。
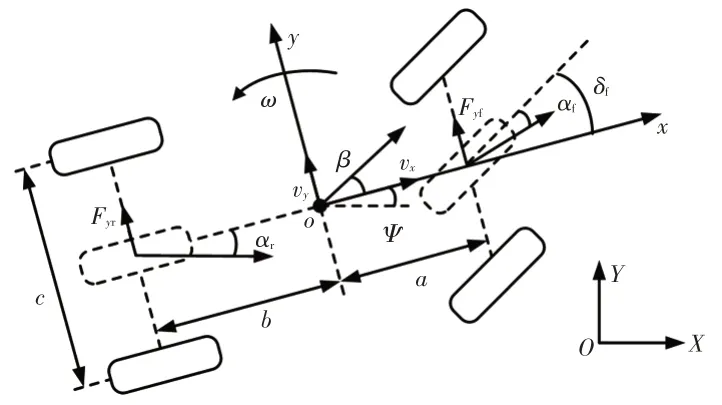
图1 车辆动力学模型
在地面坐标系中,车辆坐标(,)与行驶速度的关系为:
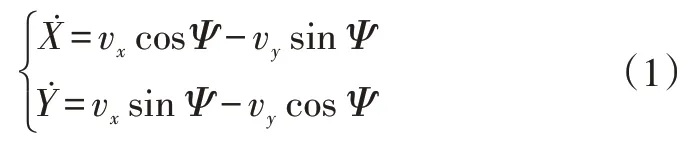
在车身固联坐标系中,根据牛顿-欧拉公式可知:
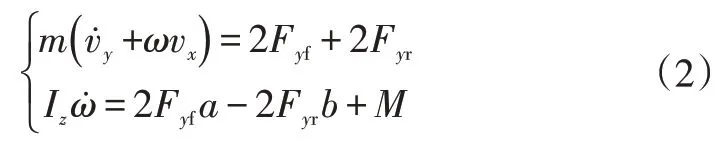
式中,F、F分别为地面作用于前、后车轮的力在车身固联坐标系轴上的分量;为左、右车轮差动制动产生的横摆力矩。
根据车辆运动的几何关系,轮胎的侧偏角满足:
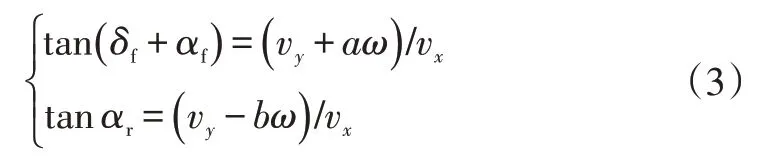
车辆的操纵几乎都是通过改变轮胎与路面的相对运动关系从而改变轮胎受力实现的。为了较好地反映轮胎力学特性在各种工况下的非线性特性,将魔术公式轮胎模型引入算法的预测模型。对于确定型号的轮胎,侧偏力为由轮胎侧偏角、纵向滑移率、垂向载荷F和路面附着系数确定的函数,即=(,,F,)。为简化计算,本文假设在预测时域内、F及均恒定,进入新的控制周期后再更新这些参数。略去次要因素,有:
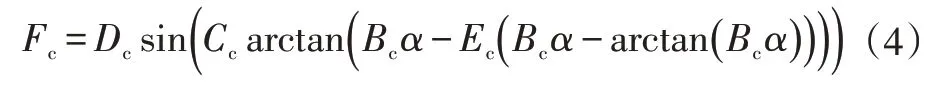
式中,、、和为系数,由具体的轮胎型号、垂向载荷和外倾角确定。
考虑到车辆以较高的速度行驶时,转向角和轮胎侧偏角一般为小角度,在轮胎坐标系和车辆固联坐标系的转换中,有:
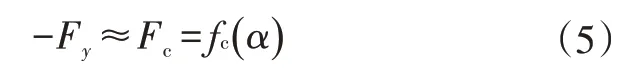
式中,F为轮胎力在车身固联坐标系轴上的分量。
记轮胎侧偏刚度的瞬时值为,则
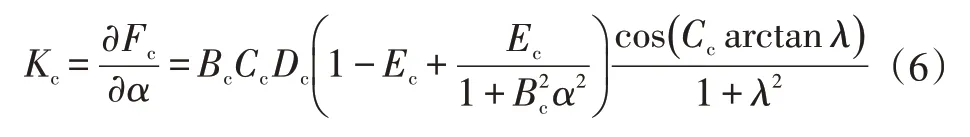
式中,=-(-arctan())。
针对控制需求,取状态量为=(,v,,),输出量为=(,),控制量为=(,),综合式(1)~式(5)得到非线性车辆动力学模型为:
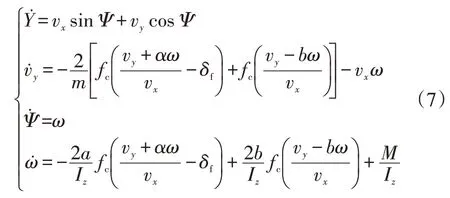
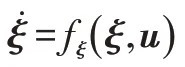
3 MPC-NPLT路径跟踪控制器设计
基于MPC-NPLT 的路径跟踪控制器利用前一周期的控制序列和非线性车辆动力学模型计算出预测时域内的预估状态运动轨迹,再沿该轨迹对模型进行线性化处理,将非线性优化问题转化为二次规划问题,以实现预测精度和在线计算量的平衡。其控制算法结构如图2所示。
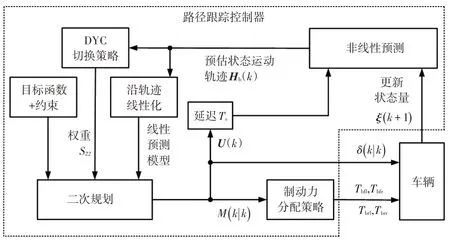
图2 路径跟踪控制器算法结构
3.1 非线性预测
记控制时域为,在每个控制周期,模型预测控制算法计算出自该时刻开始的数量为的控制量,但只实施当前控制量。在相邻的2 个控制周期所生成的控制序列中有数量为(-1)的量是重叠的,即对同一个自然时刻的系统进行重复的预测和优化。若假设前一周期的计算足够准确,可认为2个序列中重叠的控制量近似。因此,可依据前一周期得到的控制序列预估系统未来的运动轨迹。
在第个控制周期,已知上一时刻的控制序列为:
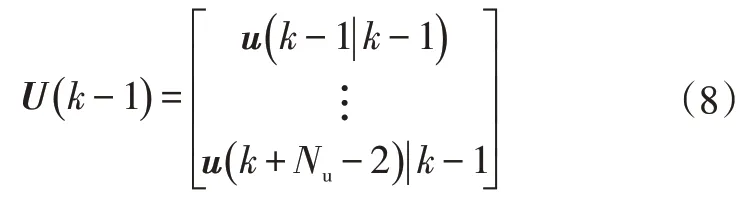
令时刻的基础控制序列为:
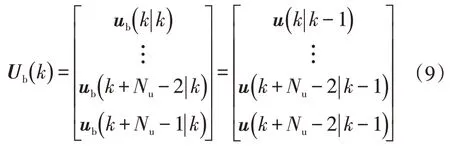
式中,为基础控制量,其在(+1)时刻保持不变。
规定系统的采样时间为,预测时域为,且≤。将式(9)作为控制量代入式(7),应用4 阶龙格-库塔(Runge-Kutta)公式得到系统状态量的递推关系为:
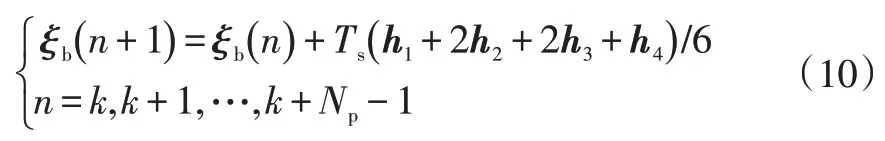
式中,()为预估的基础状态量;=f[(),()];=f[()+/2,()];=f[()+/2,()];=f[()+,()]。
解微分方程得到系统在预测时域内的预估状态运动轨迹为:
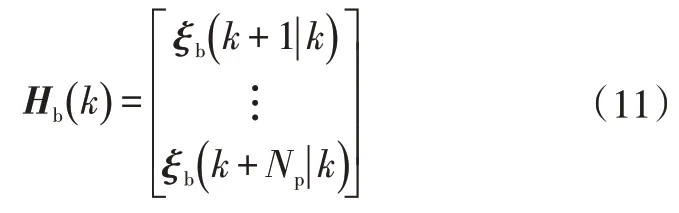
3.2 沿轨迹线性化
在第个控制周期,沿系统的预估状态运动轨迹将非线性模型作一阶泰勒展开:
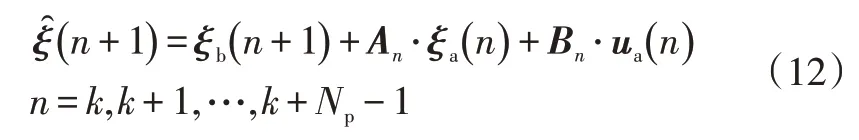
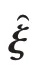
另外,定义:
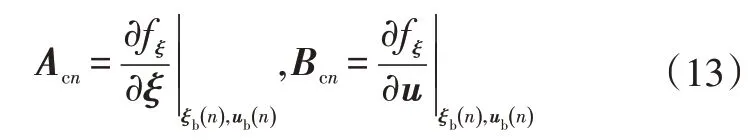
根据式(7),有:

将、离散化得:
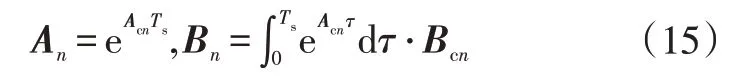
3.3 在线优化计算
综合前文,得到第个控制周期的线性预测模型为:
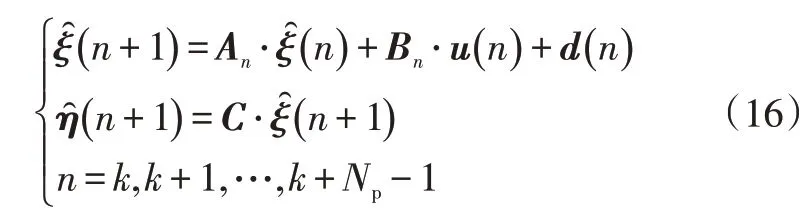
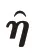
定义控制增量:
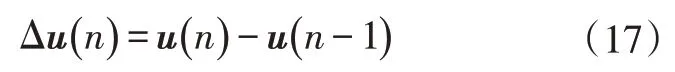
规定当≥+时,后续控制增量为零。
设计成本函数为:
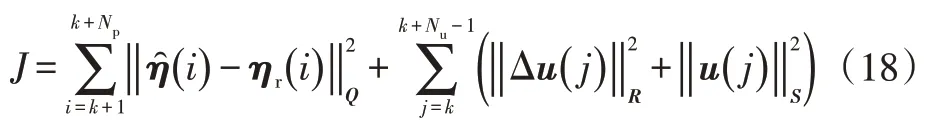
式中,()为参考输出量;为系统输出量的权重系数矩阵;为控制增量的权重系数矩阵;为控制量的权重系数矩阵。
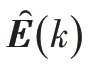

因此,式(18)又可写作:
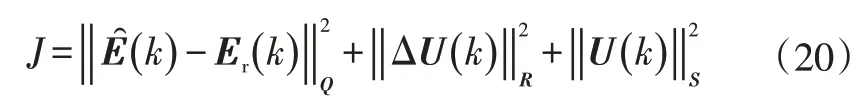
式中,()为参考输出量矩阵。
在每个控制周期求解如下优化问题:
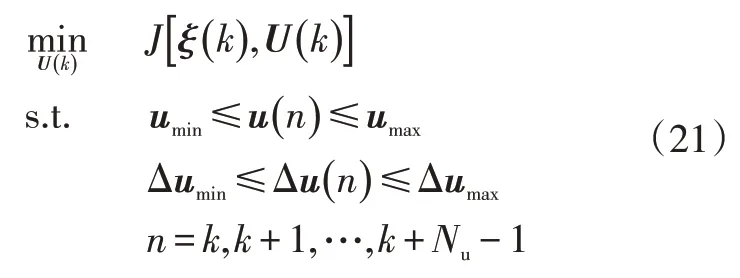
式中,、分别为控制量的最小、最大值;Δ、Δ分别为采样时间内控制量变化幅度的最小、最大值。
执行机构性能约束的引入可保证控制量的实际可行。此为带约束的二次规划问题,其计算量相对于非线性优化问题大幅减少。在求解出控制序列()后,取其中的即时控制量(|)作为实际控制量作用于转向系统。进入下一控制周期后,通过传感器和观测器更新系统的状态参数,重复上述过程,如此滚动时域地解出即时控制量即可实现车辆的路径跟踪。
3.4 直接横摆力矩控制切换策略
在极限工况下,较大的轮胎侧偏角使侧偏力饱和,导致转向系统对车辆的操纵能力不足。直接横摆力矩控制通过对各车轮的制动或驱动力矩的独立调节产生横摆力矩,从而主动地对车辆进行动力学控制,是对转向系统的恰当补充。本文采用差动制动的方式产生横摆力矩,其目标横摆力矩由模型预测控制器给出,按照一定的逻辑在各车轮上分配制动力以实现目标值。然而,车轮的差动制动会影响车辆的纵向速度,同时,其动作相对于转向系统更为粗暴,易导致乘坐舒适性变差,且频繁制动也会加速轮胎和制动系统的磨损。为改善这些问题,本文设计了直接横摆力矩控制系统的切换策略。
如前文所述,MPC-NPLT算法在每个控制周期首先会计算出预估的状态运动轨迹。根据该状态运动轨迹可估算出预测时域内的轮胎侧偏角:
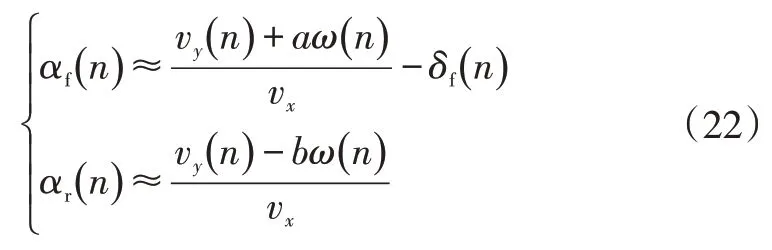
为避免频繁切换,制定如下策略:在预测时域内,即=,+1,…,+-1,对于上述方法估算的轮胎侧偏角,若存在||或||大于0.08 rad,则激活直接横摆力矩控制;若所有的||和||均小于0.06 rad,则禁用直接横摆力矩控制;在其他情况下维持上一周期的开关状态。通过调整成本函数中直接横摆力矩控制量权重系数的方式,可在不改变控制器结构的情况下实现直接横摆力矩控制系统的开关。
3.5 制动力分配策略
根据文献[17]的研究结果:当车辆后轴即将侧滑时,可在前外轮施加制动力来抑制;当车辆前轴即将侧滑时,同时制动前轮和后内轮可起到较好的效果。为减小差动制动对纵向速度的影响并避免各车轮制动力的剧烈波动,本文设计了如下制动力分配策略:
定义前、后轮负担系数分别为、:
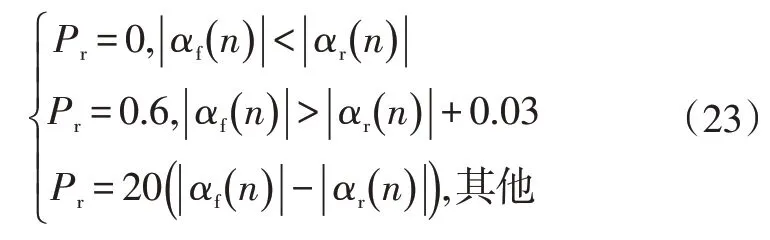
令=1-。忽略车轮的转动惯量,根据各车轮的力矩关系,当≥0时,设置制动力矩为:
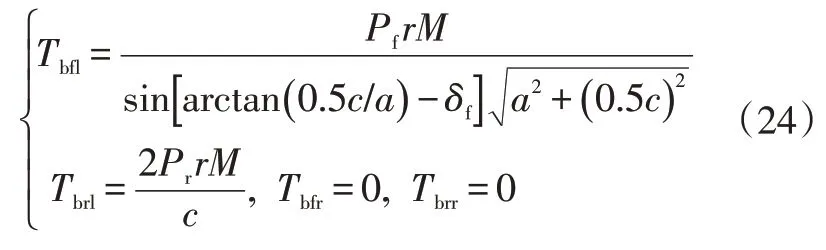
当<0时,设置制动力矩为:

式中,、分别为施加在左前轮、右前轮、左后轮和右后轮的制动力矩。
4 仿真验证与性能对比
4.1 仿真环境与参数设置
本文基于MATLAB/Simulink 开发了MPC-NPLT 车辆路径跟踪控制器。为提高仿真精度,采用CarSim 软件的高精度车辆动力学模型作为控制对象。车辆参数如表1所示。
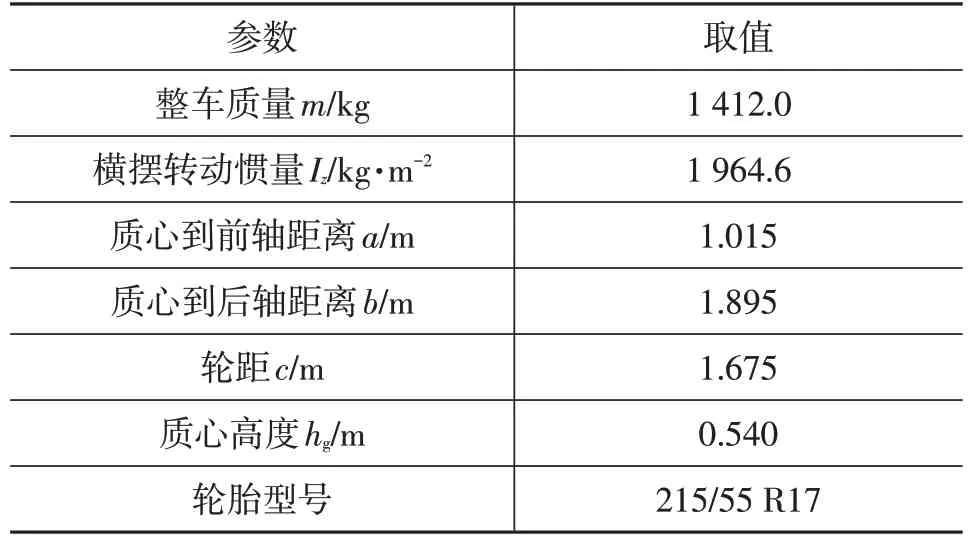
表1 车辆参数
仿真中采用的控制器参数如表2 所示,其中、、、、、分别为矩阵、、的对角元素,、、中其余元素均为0。。
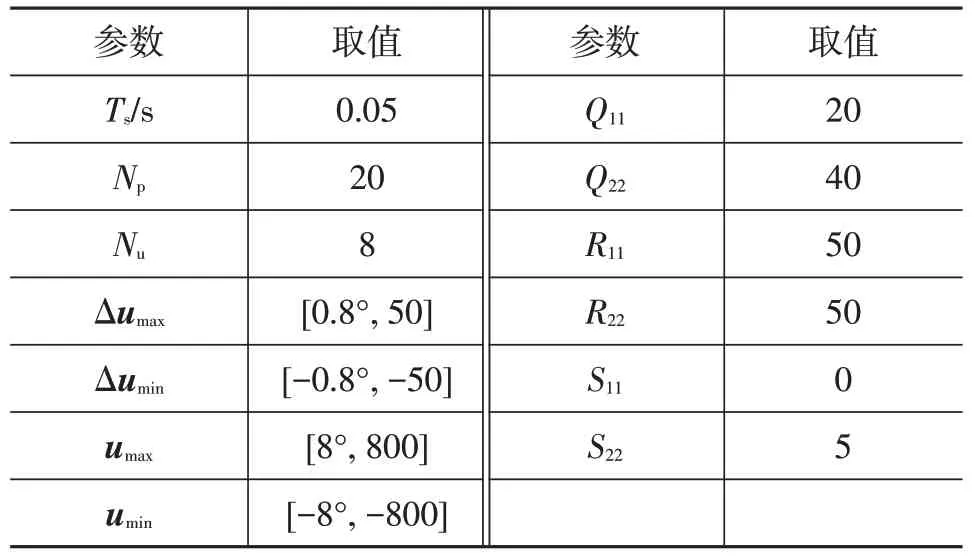
表2 控制器参数
原始参考路径以纵、横坐标的散点序列给出,首先采用三次样条插值,使其连续化。插值结果是以给定数据点区间分段的三次多项式,记为。其二阶导数连续,可保证参考航向角的平滑性。参考航向角的多项式满足:
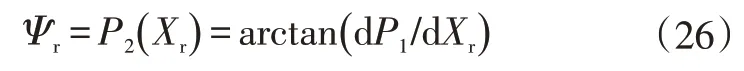
式中,为参考航向角;为参考纵坐标。
另记Y为参考横坐标,故参考输出量为=(,)。
4.2 仿真结果与分析
为验证并对比算法的控制效果,搭建了3种路径跟踪控制器。控制器1 基于LTV MPC,控制器2 基于MPC-NPLT,控制器3 基于MPC-NPLT 并加入了直接横摆力矩控制系统及其切换策略。分别取行驶速度为72 km/h 和108 km/h,在路面附着系数为0.85 的平坦路面进行双移线仿真测试,结果如图3所示。
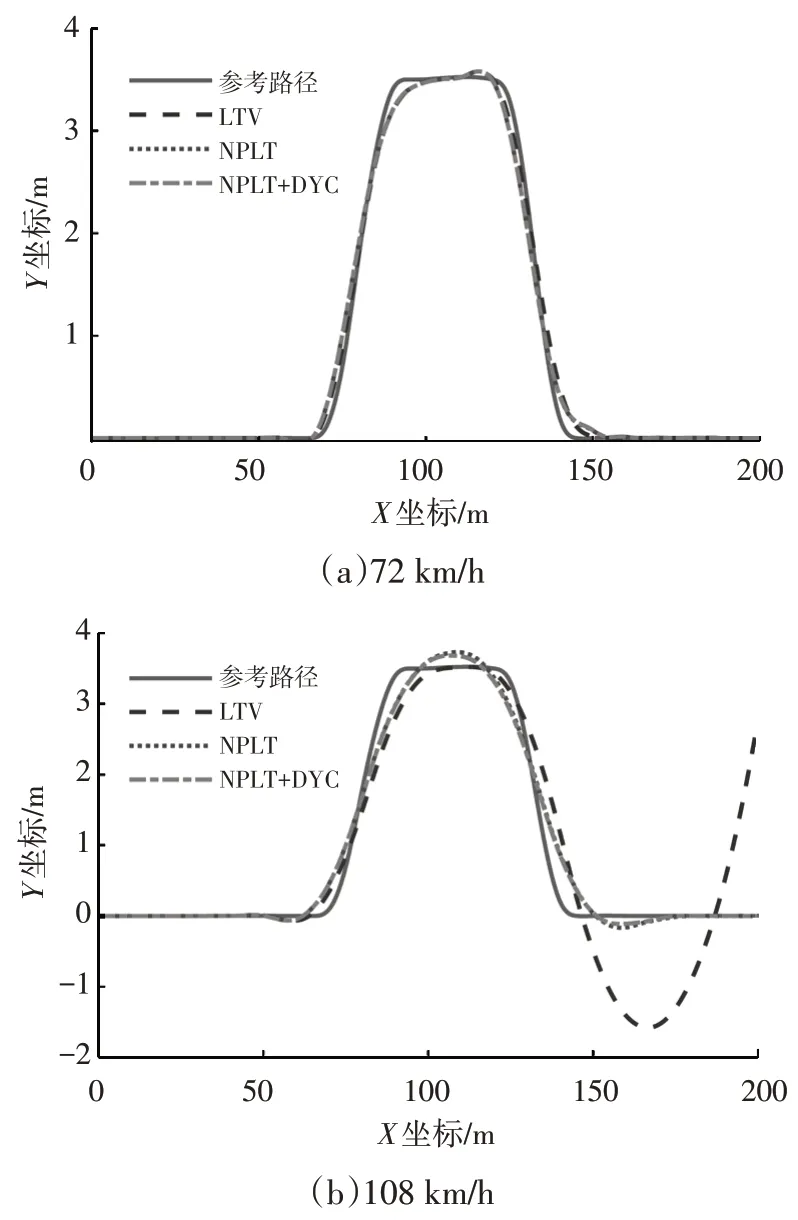
图3 不同车速下的仿真结果对比
由图3可知:车速为72 km/h时,轮胎侧偏力尚未到达饱和区,2 种算法的预测精度相近,控制效果差别不大;车速为108 km/h 时,轮胎侧偏力在车辆变换回原车道的过程中接近饱和,此时LTV MPC 算法的预测模型与实际车辆动力学模型出现较大差别,导致车辆偏离了对参考路径的跟踪;得益于更高的预测精度,MPCNPLT算法在车辆进入动力学非线性区时仍能提供较好的控制效果,使车辆在经过小幅的超调后能够迅速回到参考路径上。
图4展示了控制器3在72 km/h的仿真中,根据预测的轮胎侧偏角实时切换横摆力矩控制系统开关状态的情况。由图4可知:当系统预测到未来一段时间内轮胎侧偏角的绝对值可能超过0.08 rad 时,会激活直接横摆力矩控制系统;若轮胎侧偏角绝对值始终在0.06 rad 以下,则会关闭直接横摆力矩控制系统。图5 所示为第3.0~7.5 s 的时间段内系统根据直接横摆力矩目标值分配给各车轮的制动力矩。由于路面附着系数较大,尽管轮胎侧偏力进入非线性区,但仍能提供足够的操纵力,因此各车轮制动力矩都不大,横摆力矩控制系统的引入没有对路径跟踪效果产生显著的影响。
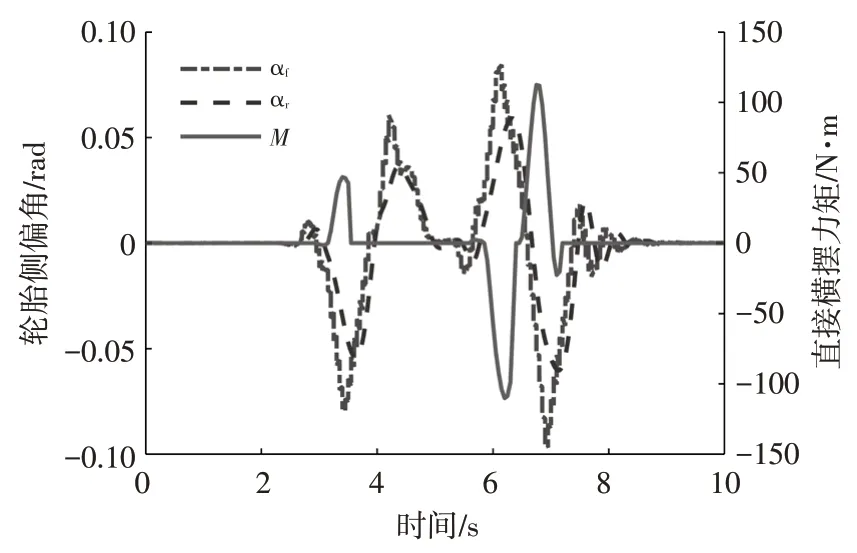
图4 侧偏角-直接横摆力矩

图5 制动力矩分配
为进一步验证在较低附着系数的路面上引入直接横摆力矩控制的效果,设置行驶速度为90 km/h,路面附着系数为0.5。仿真结果如图6 所示:不具备直接横摆力矩控制的算法虽然仍能够操纵车辆跟踪参考路径,但由于路面附着系数较小,轮胎侧偏力饱和后操纵能力下降,在车辆返回原车道时有约1.758 m的跟踪误差;具备直接横摆力矩控制的算法通过独立调节施加到各车轮的制动力,在轮胎侧偏力饱和时仍有足够的横摆操纵能力,使车辆平滑、稳定地变换回原车道。仿真结果证明了引入直接横摆力矩控制切换策略和制动力分配策略后能够进一步改善在较低附着系数路面上的跟踪效果。
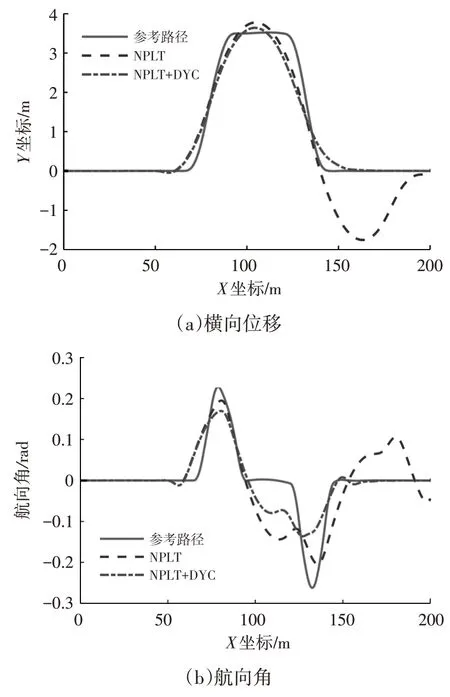
图6 有无直接横摆力矩控制的仿真结果对比
在此基础上,采用具备直接横摆力矩控制切换策略和制动力分配策略的MPC-NPLT 算法在更低附着系数的路面进行仿真。设置车辆行驶速度为60 km/h,仿真结果如图7所示。分析结果可知:随着路面附着系数减小,轮胎的侧向力和纵向力更易饱和,所能提供的操纵力和操纵力矩减小,导致车辆的路径跟踪误差略有增大;得益于对轮胎力的充分利用,即使在附着系数为0.2的路面上,所提出的控制方法仍能保持车辆运动状态可控,使车辆稳定地跟踪参考路径。仿真结果验证了该方法在低附着系数路面上的路径跟踪控制效果。
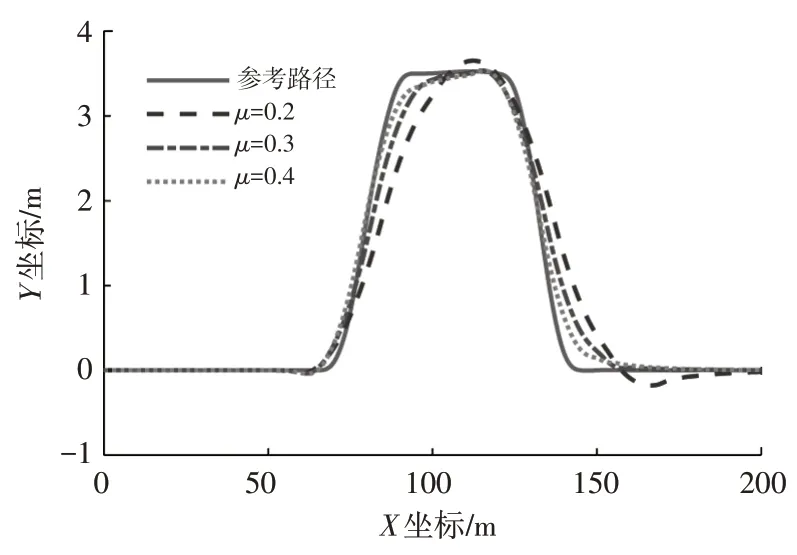
图7 低附着系数路面的仿真结果对比
5 结束语
本文针对车辆路径跟踪模型预测控制的动力学非线性问题和实时性要求,引入了MPC-NPLT 算法。通过非线性预测和沿轨迹的线性化,将非线性因素从优化计算中排除,使其转化为二次规划问题,显著减小了在线计算量。Simulink及CarSim联合仿真结果表明:基于MPC-NPLT 的车辆路径跟踪控制方法在各种行驶速度工况下均能实现稳定的路径跟踪,相对于LTV MPC 算法在动力学非线性区具有更好的控制效果;所设计的切换策略较好地协调了直接横摆力矩控制和转向控制;制定的制动力分配策略提高了车辆在较低附着系数路面上的路径跟踪能力。
