围绕一个“联”字
2022-04-08施惠芳
施惠芳

摘要:复习课不能定位为对基础知识、基本技能的练习,采用“走过场”“炒冷饭”“题海战”的方式进行。《小数四则运算(复习)》一课围绕一个“联”字展开,引导学生用联系的观点看待问题,具体做法是:主问题驱动,在联系中唤醒思维;大跨度梳理,在联系中整体建构;深挖掘算理,在联系中抵达本质。
关键词:小数四则运算;复习课;联系
《小数四则运算(复习)》一课的教学目标确定为:(1)通过复习,理解加、减、乘、除运算的意义及其关系,从整体上理解和掌握小数四则运算的算理与算法。(2)通过四则运算方法的共性与差异比较,理解计数单位在加、减、乘、除运算中的统领作用,建立数与运算的整体结构,沟通小数四则运算与整数四则运算的关联。(3)学会用整体性思维、结构化思维梳理旧知,形成认知结构。本课教学过程与思考如下:
一、教学过程
(一)相关知识的梳理与回顾
师今天我们一起上一节四则运算的复习课。说起四则运算,你想到了什么?(加、减、乘、除)加、减、乘、除,同学们熟悉吗?无论是生活中,还是学习中,我们每天都在使用四则运算。你看,我们从小学一年级开始就接触四则运算了,你还记得我们经历了怎样的学习历程吗?
教师依次出示历册教材中的相关内容。
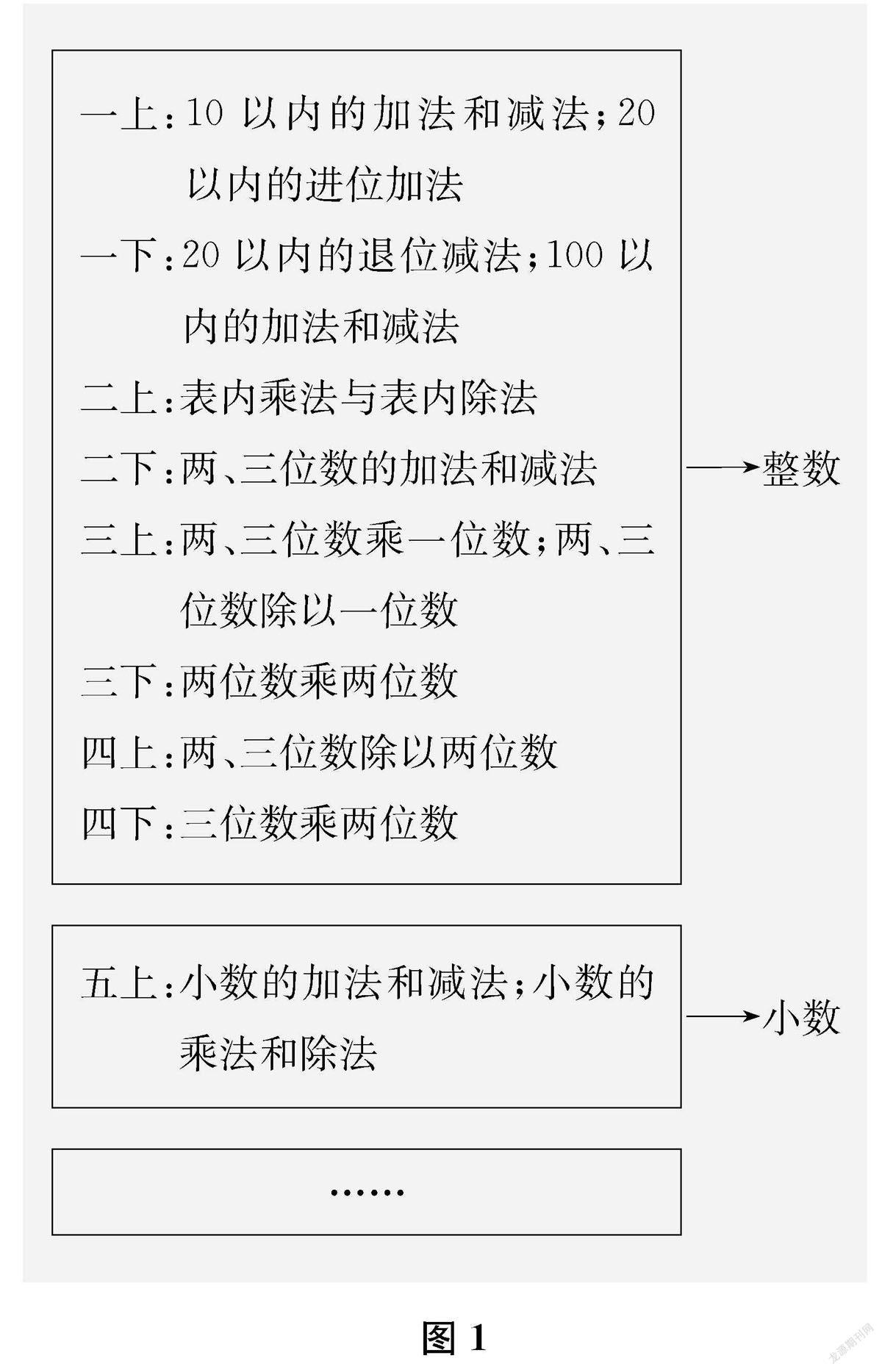
师仔細回顾我们的学习过程,你有什么发现?(由易到难,加、减、乘、除运算交织着学习……)从一年级一直到四年级,其实我们都在学习关于什么数的四则运算?(整数)五年级学习的是什么数的四则运算?(小数)将来我们可能还会学习什么数的四则运算?(分数)
出示图1。
师你有什么想问的?(为什么整数四则运算要学习四年,而小数四则运算只要学一个学期?为什么加、减、乘、除运算要交织着学习?)看来,小数四则运算与整数四则运算有着紧密的联系。
师今天这节复习课,我们就围绕一个“联”字,用联系的观点开展复习,看看能不能发现不一样的数学。
[说明:突出联系的观点,着眼知识纵向与横向的整体性。这节课是对五年级上册“小数加、减、乘、除运算”的复习和整理,更是对“数的运算”这一主题内容的一次整体梳理和建构。因此,从回顾四则运算的学习历程入手,引导学生反思,并引发学生提出核心问题“为什么整数四则运算要学习四年,而小数四则运算只要学一个学期”,达成从“联”字入手复习的共识。]
(二)理解四则运算的意义与关系
师无论是整数四则运算还是小数四则运算,想要理解四则运算的意义,必须寻找它们在生活中的故事。课前,同学们都在生活中寻找了一些数学小故事,四人小组交流一下:什么样的问题情境用加法?什么样的问题情境用减法?乘法、除法呢?
师几个部分合成一个整体,就用加法;从整体中去掉若干个部分,就用减法。加法就是从部分到整体,减法就是从整体到部分,减法是加法的逆运算。如果几个部分是相同的,合成一个整体时,我们还可以用乘法,乘法是加法的简便运算。除法就是平均分,从整体中不断减掉相同的部分,如12÷4→12-4-4-4,除法实际也是在做减法,除法是乘法的逆运算。
师加、减、乘、除运算之间有着怎样的关系?有了加法,就产生了——(减法)为什么这么讲?(减法是加法的逆运算)有了加法,还会产生什么?(乘法)有了乘法就产生了——(除法)为什么这么讲?(除法是乘法的逆运算)除法与减法有关系吗?
师你发现加、减、乘、除运算中谁是源头?(加法)过去,我们都认为加法是加法,减法是减法,乘法是乘法,除法是除法,通过讨论我们发现加与减、乘与除互为逆运算,又知道加法是核心,其他的运算都是由它生长出来的,还知道无论是小数四则运算还是整数四则运算,意义是一致的。用联系的观点看问题,就能发现不一样的数学。
[说明:突出加法的核心地位,沟通四则运算意义的关联。对于运算的意义,学生虽然已经能通过列算式、讲故事等方式体现认识,但大多数学生还是会认为加是加,减是减,乘是乘,除是除。本课试图从整体结构的角度带领学生打通加、减、乘、除的意义,让学生构建整体结构化的知识体系,让核心概念和关键能力更有生长性。在梳理中明确加法是四则运算的源头,学生不仅能进一步体会加、减、乘、除的意义,巩固加法和减法、乘法和除法的逆运算关系,还能感受到乘法是相同加数累加的简便运算,除法是连续减去几个相同数的简便运算,沟通加、减、乘、除意义之间的关联,建立整体的知识结构。]
(三)巩固四则运算的算理与算法
师分别举例说明小数加、减法与整数加、减法的联系,小数乘法与整数乘法的联系,小数除法与整数除法的联系。
学生交流,反思质疑:为什么这样计算?有什么道理?
师(加、减法的比较)为什么要数位对齐,不对齐会怎样?数位对齐是为了找到相同计数单位的数。
师(乘法的比较)乘出的结果怎么点小数点?通过0.1乘0.1积的计数单位来理解小数乘法积的小数点位置,由这个算式你还想到了哪些乘法算式?
师(除法的比较)跟计数单位有关系吗?(细分计数单位)小数点在哪里?为什么商的小数点要与被除数的小数点对齐?看到这个算式,你想到哪些除法算式?
师不管做加法、减法,还是做乘法、除法,虽然是不同的运算,但是支撑运算过程,帮助我们理解运算道理,都离不开——计数单位。
师(出示对比练习,见图2)。第一组计算特别要注意什么?第二组哪一个算式是核心算式?第三组先算哪一个?其他算式的结果你能直接知道吗?
[说明:突出计数单位的统领地位,感悟四则运算本质的一致性。学生能正确计算出结果就是理解道理了吗?如何沟通加、减、乘、除运算的算理,感悟运算本质的一致性,提高学生的运算能力呢?通过复习,纵向沟通整数、小数运算之间的关联,横向沟通无论是小数的加法、减法还是乘法、除法,其本质都是要解决好计数单位的问题。]
(四)总结与拓展
师通过今天的复习课,你有什么收获?
师同学们,回顾今天的复习,我们一直在用一种怎样的视角研究问题?(联系)我们既横向梳理了加、减、乘、除的关系,也纵向比较了整数、小数四则运算的关系,如果继续用这样的眼光去看待今后要学习的分数四则运算,你有什么启发?
师数学是有联系的,数学是有结构的。数学知识那么多,如果我们能找到核心、抓住本质、理清结构,就可以把复杂的数学学简单。
二、教学思考
复习课是什么?有什么功能?如果把复习课定位为对基础知识、基本技能的练习,采用“走过场”“炒冷饭”“题海战”的方式进行,学生难免心生厌倦,涉及的知识也会显得支离破碎,复习就起不到查漏补缺、质疑问难、拓展提升、思维进阶的作用。因此,正确认识复习课的功能尤为重要。我认为,复习课需在联系中唤醒思维、整体建构、抵达本质。《小数四则运算(复习)》一课教学据此展开。
(一)主问题驱动,在联系中唤醒思维
复习课首要的任务是唤醒已学的知识。本节课教学前,我利用前置学习单设计问题,引导学生自主回顾与整理。具体问题包括:(1)分别编写一个用整数或小数加法、减法、乘法、除法解决的数学问题,并通过计算来解决。(可以是相关联的同一故事的不同问题,也可以是不同故事的不同问题)(2)举例说明:整数加、减运算与小数加、减运算有什么联系?(3)举例说明:整数乘、除法与小数乘、除法有什么联系?问题(1)基于四则运算与真实生活情境的融通,建立数学知识与生活现实的联系;问题(2)、问题(3)基于整数四则运算与小数四则运算算理与算法的对比,建立新旧知识的关联。课上依学而教,有针对性地组织交流、补充。而更为上位的目标,是唤醒学生发现问题、提出问题、分析问题、解决问题的意识与能力。因此,“为什么整数四则运算要学习四年,而小数四则运算只要学一个学期?”这一问题,成为统领整节复习课的主问题,它唤醒了学生用联系的观点看待问题的意识,唤醒了学生主动对照、主动寻求联结点、主动建构知识的欲望,唤醒了学生深度探寻知识本质的思维。
(二)大跨度梳理,在联系中整体建构
数学学科的知识结构是一个纵向和横向紧密联结的网状结构。然而,教师不可能直接把完整的知识结构呈现给学生,而要通过一册一册教材、一个一个单元以及一节一节课时的教学逐步累积形成。学生获得的知识如果没有完满的结构把它们连在一起,多半是会被遗忘的。这就要求教师对相关知识进行整体架构,通过联结点引导学生把数学大厦建得结构完整、结实美观。基于这样的认识,我觉得综合复习课中的大跨度梳理,是促进学生形成完整认知结构的契机。因此,在确定本课的教学目标时,我把“联系”作为核心。纵向来看,需要勾连整数与小数四则运算之间的关系;横向来看,需要勾连加、减、乘、除运算相互的关系。
(三)深挖掘算理,在联系中抵达本质
学生能正确计算出结果,就是真正理解算理了吗?如何加深学生对加、减、乘、除运算算理的理解,促其感悟运算本质的一致性,进而提高运算能力呢?教学中,我把学习任务转化成核心问题序列,引导学生自由选举例子进行交流,并追问:“整数加、减法的竖式计算为什么强调末尾对齐?小数加、减法的竖式计算为什么强调小数点对齐?”这样的追问,让学生豁然开朗:原来,无论整数还是小数相加、减,只有将相同的计数单位个数相加、减,才能保证计算结果的正确性。“一位小數乘一位小数的积为何是两位小数?”这一问引导学生用数形结合的观点来分析解释。“为什么商的小数点要与被除数的小数点对齐?”这一问则让学生明确分的对象与结果的计数单位的一致性,感悟数的运算与运算对象的关系,体会数的运算本质上的一致性。通过全面对比,学生头脑中自然形成了以计数单位为核心的整体知识结构,也增强了推理意识。通过复习,纵向沟通整数、小数运算之间的关联,横向沟通四种运算之间的关联,这样的梳理也为今后学习分数的四则运算奠定基础。
