仿人机械臂的设计与轨迹规划分析

王欣然,王春荣*,夏尔冬,卫 沅,熊昌炯

（1.三明学院 机电工程学院，福建 三明 365004；2.河南科技大学 车辆与交通工程学院，河南 洛阳 471003）

由于机械臂灵活性能好，在各个领域中得到了广泛的应用[1-2]，随着计算机科学技术与人工智能的发展，机械臂的各方面性能得到了进一步的提升.仿人机械臂是以人臂为参照，与人臂具有较高的相似度，其运动性能更加优越，是当前机器人领域的研究热点[3-4].

杨涛等[5]对7自由度的仿人机械臂同步控制进行了研究，提高机械臂的控制精度.王巍等[6]构建了仿人双机械臂的协同模型，并对其运动规划进行了研究，使其能高效且无碰撞地完成相关任务.唐跃嘉[7]基于人体工程学分析了仿人机械臂的构型.霍希建等[8]提出了一种自寻优方法对7R 仿人机械臂的逆运动学进行了优化.王春荣等[9]提出了一种分级规划策略对仿人机械臂的拟人运动进行了研究.刘晶晶等[10]基于MATLAB对仿人机械臂的正逆运动学进行了分析.

本文以人臂为参考对象，设计了一款与人臂高度相似的仿人机械臂，并已经获得国家授权专利[一种仿人机械臂（ZL201620675819.2）][11].主要研究内容是通过建立仿人机械臂的D-H 坐标系，分析了其正逆运动学问题；并利用MATLAB的Robotic-Toolbox对仿人机械在直角坐标系与关节坐标系下的轨迹规划进行了分析，研究表明所设计的机械臂结构合理，能按照设定的任务点平稳地完成任务.

1 仿人机械臂的设计

为了能够使机械臂与人臂具有较高的相似度，在机械臂的肩关节设计了3个转动关节（关节1、关节2和关节3）模拟人臂肩关节的球窝机构；在机械臂的肘关节与腕关节分别设计了1个转动关节（关节4）和2个转动关节（关节5和关节6）模拟人臂的肘关节与腕关节.设计的仿人机械臂三维模型图如图1所示，从图1中可以发现所设计的机械臂除了上述6个关节之外，还具有与人手指非常相似的机械手指机构.

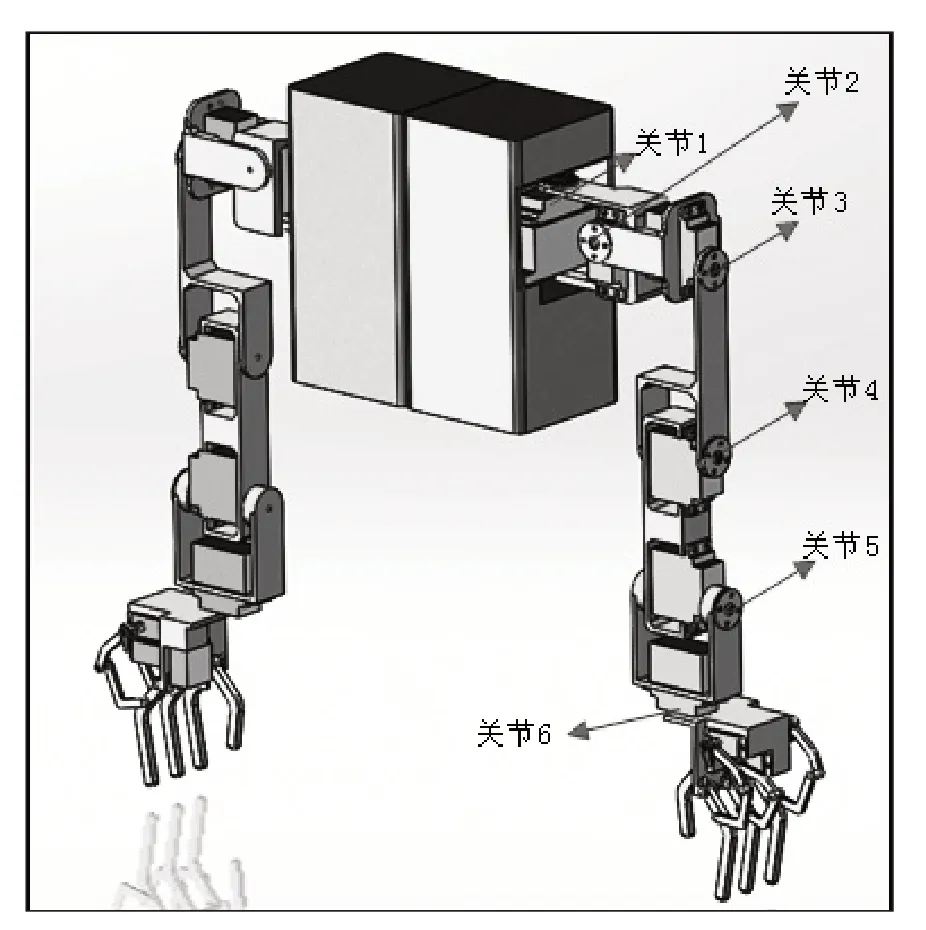
图1 仿人机械臂三维模型

2 仿人机械臂运动学分析

2.1 D-H坐标系

1956年，Denauit等[12]提出了一种严格定义机械臂中各个连杆的坐标系与关节的方法，即D-H法.结合以上分析，设计的仿人机械臂具有6个转动关节，根据D-H法建立其D-H坐标系，如图2所示.并根据所建立的D-H坐标系可获得相应的D-H坐标参数，如表1所示.

表1 D-H坐标参数

图2 仿人机械臂D-H坐标系

2.2 运动学方程

通过建立仿人机械臂D-H 坐标系，并获得其D-H 坐标参数后，即可分析相邻两杆之间的相对位姿关系，经过齐次变换可使连杆i-1的坐标系与连杆i坐标系重合.齐次变换矩阵Ai为

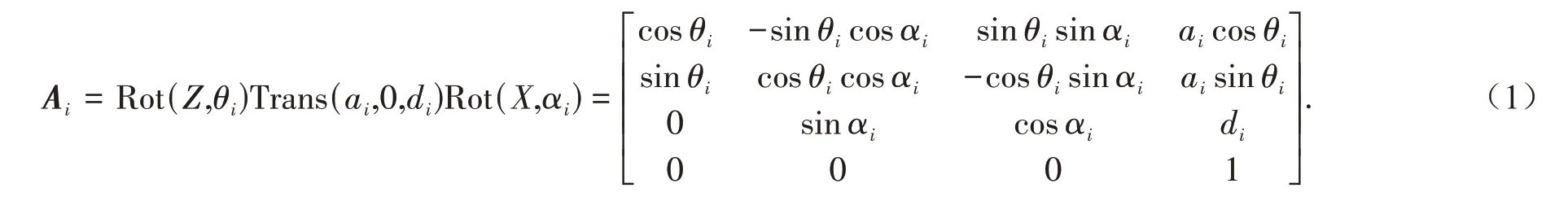
根据表1的D-H参数可得

即可得仿人机械臂的运动方程为

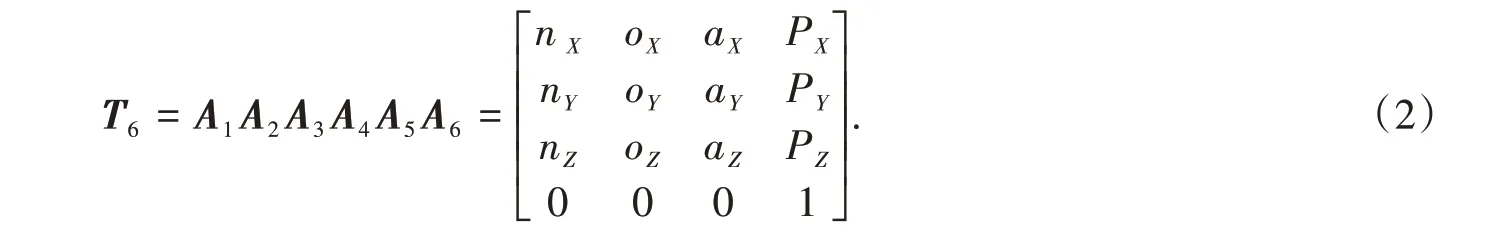
2.3 正、逆运动学分析

利用MATLAB的Robotic-Toolbox中的“link”函数，并根据表1中的D-H坐标参数建立仿人机械臂的仿真模型，如图3 所示；仿人机械臂驱动界面，如图4 所示.从图4 中可以看出，机械臂在初始状态时，末端执行器位于点A=（307，0，-95）.

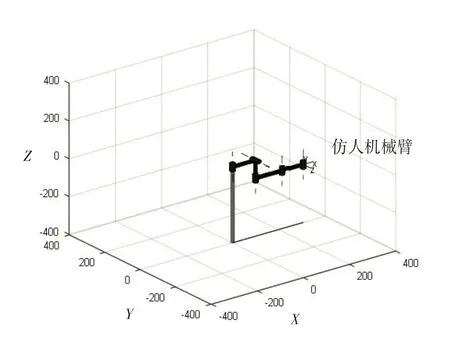
图3 仿人机械臂仿真模型

图4 仿人机械臂驱动界面

设机械臂从初始位置A=（307.000，0，-95.000）、关节角q=[0，0，0，0，0，0]，运动至位置B=（306.599，-94.823，-47.943）、关节角q=[-0.300，0.220，-0.120，0.270，0.460，0.760].利用“fkine”函数求得仿人机械臂末端执行器相对于基座的坐标系的齐次变换矩阵为：

设机械臂末端执行器的位姿为T6，利用“ikine”函数研究仿人机械臂的逆解问题，可得各个关节角为q=[-0.300，0.220，-0.120，0.270，0.460，0.760].仿真实验表明，机械臂的逆解具有唯一性，正逆解相符，同时也证明了机械臂设计的合理性.

3 轨迹规划

为了使仿人机械臂在其运动空间中达到指定的位置，需对其进行轨迹规划研究.在实际的工程应用中，操作人员往往希望机械臂能按照实际应用的轨迹进行运动，如直线、圆弧或者其他轨迹.将分析仿人机械在直角坐标系中的直线与关节坐标系中的曲线的轨迹规划问题，以验证仿人机械设计的合理性.

3.1 直角坐标系

设机械臂末端执行器从初始位置A=（307.000，0，-95.000）做直线插补运动至位置B=（257.660，148.097，79.328）.利用“jtraj”函数分析机械臂在直角坐标系下的直线插补轨迹，设定仿真时间为20 s，仿真间隔时间为0.1 s，插补轨迹如图5所示，插补过程各个关节角的位移、角速度与角加速度如图6所示.

图5 直线插补轨迹图

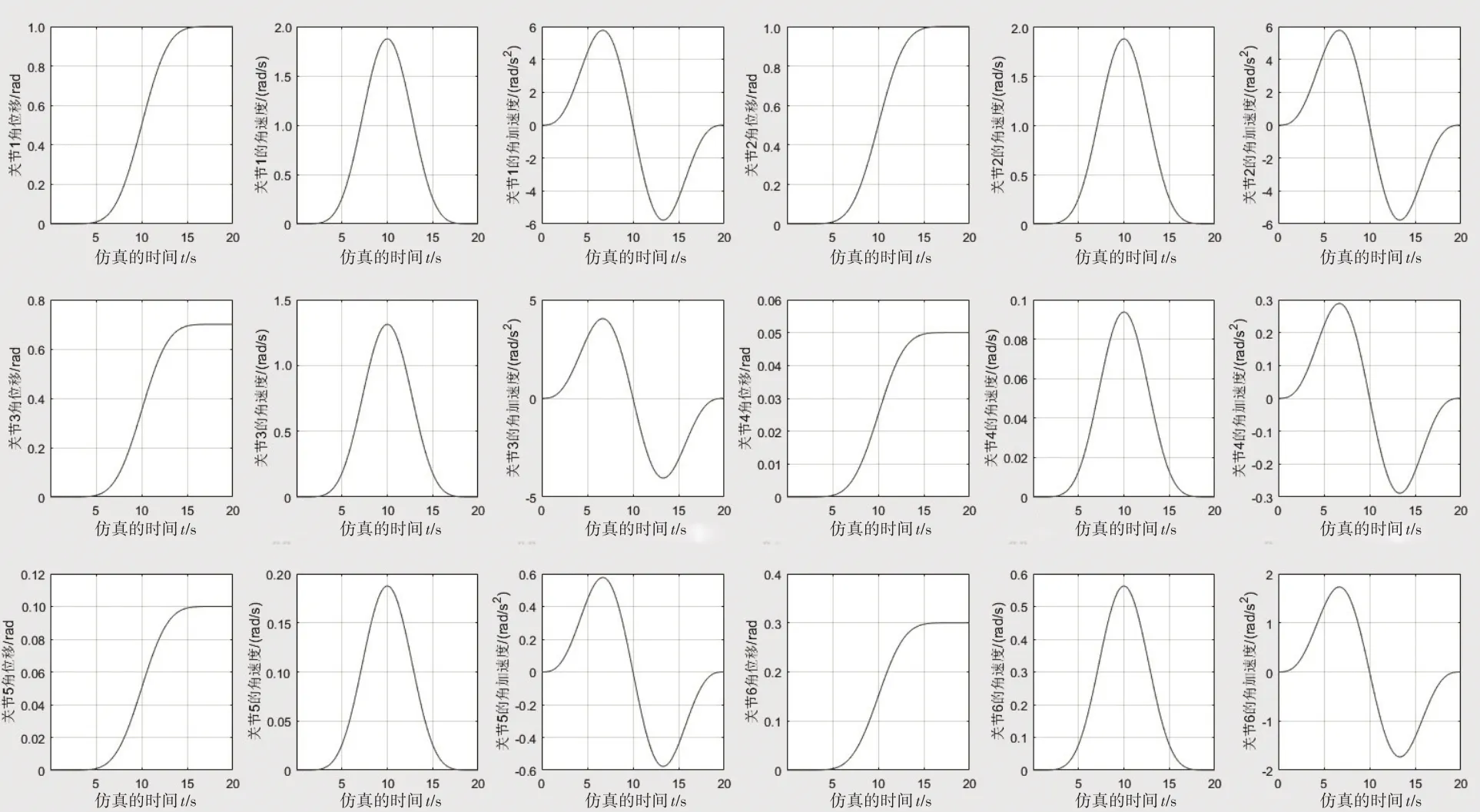
图6 各关节的角位移、角速度和角加速度

3.2 关节坐标系

直角坐标系下对机械臂的轨迹规划具有较为严格的要求，但在上述的直线插补过程中，并非所有的插补点都有逆解.此时，可通过研究机械臂在关节坐标系下的两点之间的圆弧插补，以实现机械臂相应的轨迹规划.所设计的仿人机械臂在关节坐标系中完成上述两点之间曲线插补轨迹如图7所示，各个关节的角位移、角速度和角加速度如图8所示.

图7 曲线插补轨迹图

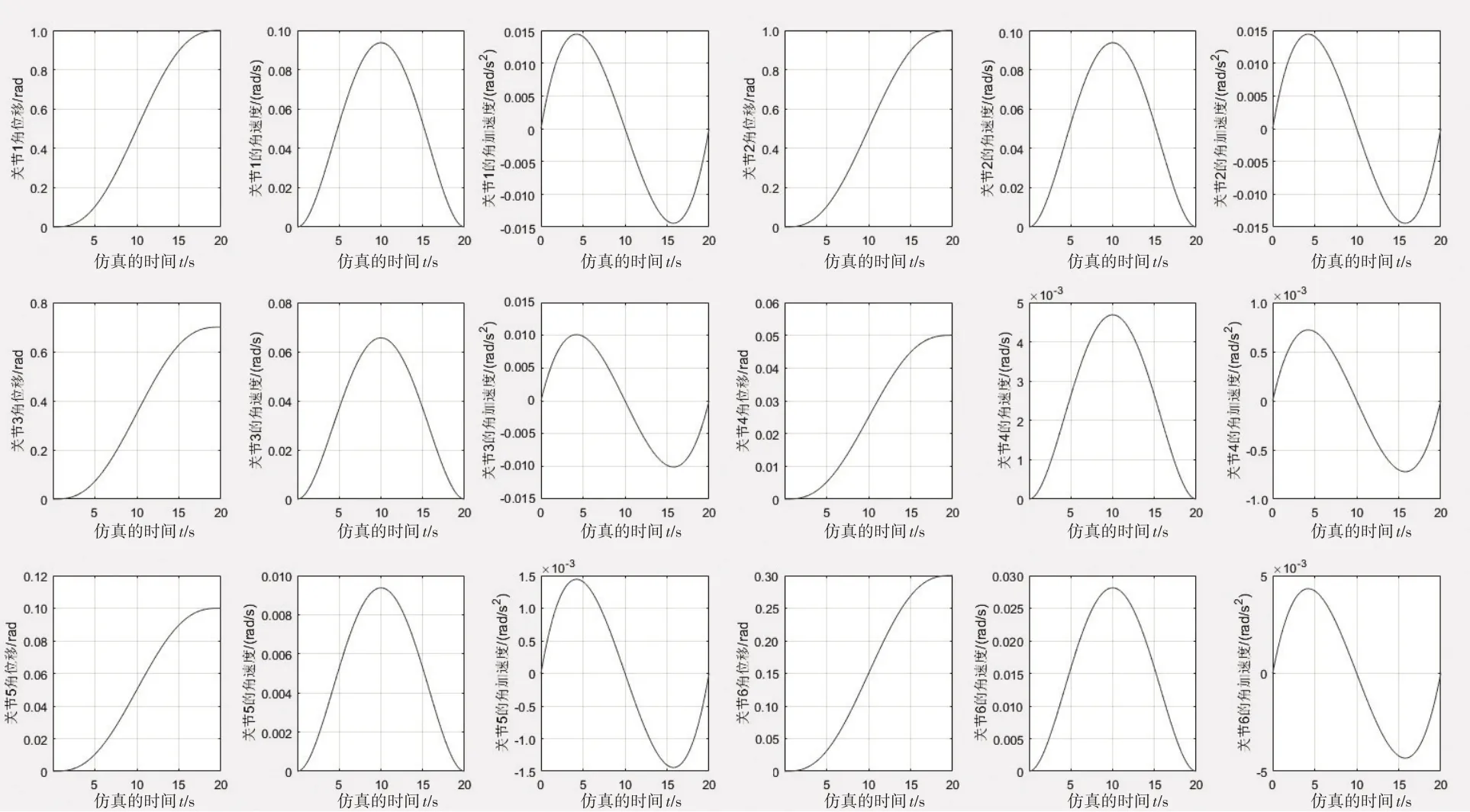
图8 各关节的角位移、角速度和角加速度

从仿真实验结果可以发现，仿人机械臂在直角坐标系下的直线插补与关节坐标系下的圆弧插补的轨迹规划都非常平稳、无跳跃现象；各个关节的角位移、角速度与角加速度的变化均非常地均匀、连贯,无跳跃现象，角速度与角加速度在初始位置与终止位置均为0.

3.3 复杂轨迹规划

机械臂在执行实际任务过程中所运行的轨迹一般不是均为直线运动或者曲线运动，而是包含了直线运动与曲线运动.因此，本节分析机械臂末端执行器从初始位置A=（307.000，0，-95.000）做直线插补运动至位置B=（189.334，94.584，104.257），然后再从位置B做曲线插补运动至位置C=（-159.378，214.964，-63.778），直线插补与曲线插补的仿真时间各为10 s.插补轨迹如图9 所示，各个关节的角位移、角速度和角加速度如图10所示.

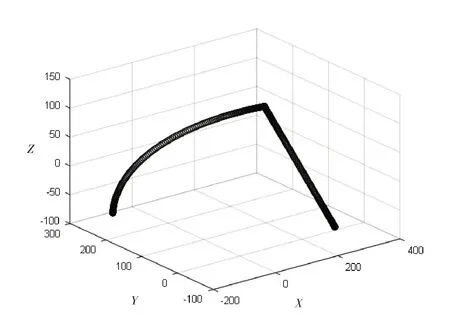
图9 复杂轨迹插补轨迹图

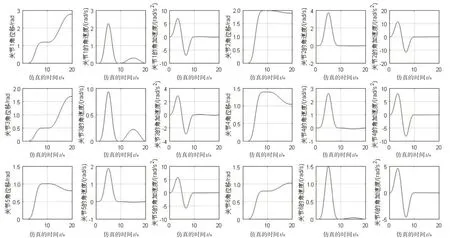
图10 各关节的角位移、角速度和角加速度

分析仿真结果可知，仿人机械臂各关节的角位移、角速度与角加速度在直线运动、曲线运动以及二者的连接过渡时的变化均非常地均匀、连贯、无跳跃现象，角速度与角加速度在初始位置与终止位置均为0.

通过仿真实验表明，设计的仿人机械臂在直线运动、曲线运动以及复杂的轨迹插补过程中均具有良好的特性，表明所设计的机械臂结构合理、能满足相应的轨迹规划要求.

4 结束语

通过对人臂构型的研究，设计了一款仿人机械臂.通过建立仿人机械臂的D-H 坐标系，分析了其正逆运动学，并通过MATLAB 对其在直角坐标系下直线插补、关节坐标系下圆弧插补以及复杂轨迹的轨迹规划进行了研究，结果表明所设计的仿人机械臂机构合理.通过研究分析可减少机械臂的设计成本，具有一定的理论指导意义.