亚纯函数与其n阶差分的唯一性

林鸿金,陈省江

(1.福建师范大学数学与统计学院,福建福州 350117；2.宁德师范学院数理学院,福建宁德 352100)

1 引言及主要结果

假设读者已经熟知了Nevanlinna值分布理论和Nevanlinna差分模拟理论中的基本理论和符号[1-2],例如N(r,f),m(r,f),T(r,f)等.

通常所说的亚纯函数指的是在整个复平面上亚纯.如果说f(z)和g(z)为亚纯函数,a∈C⋃{∞}为任一复数.若f(z) -a和g(z) -a的零点相同且每个零点的重级也相同,则称f(z)和g(z)CM 分担a.若f(z) -a和g(z) -a有相同的零点(不计重数),则称f(z)和g(z) IM分担a.

设f为复平面上的亚纯函数.对于任意的非常数亚纯函数f(z),S(r,f)=o{T(r,f)},r→∞,可能需除去一个对数测度为有限的例外值.亚纯函数f(z)的级和超级分别为

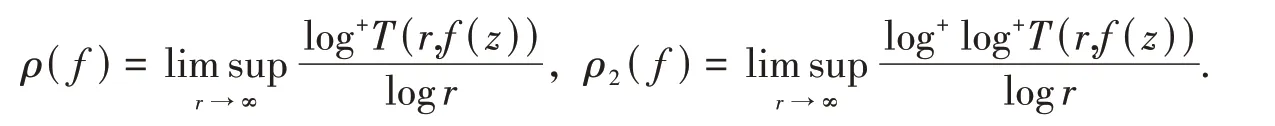
亚纯函数f(z)的一阶差分及其n阶差分定义如下:设c为非零复常数使得f(z+c) ≢f(z),有

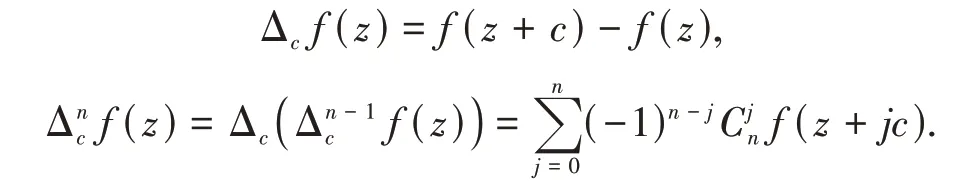
设a为任意复数,定义亏量如下:

有穷级亚纯函数的Nevanlinna 差分模拟理论是由Halburd 等[3]、Chiang 等[4]分别建立的.随后,Halburd 等[5]等将有穷级亚纯函数推广为超级严格小于1 的亚纯函数,这给复差分方程和唯一性理论的研究提供了强有力的支撑.近年来,不少学者研究两个亚纯函数分担“2CM+1IM”的问题.

2012年,Chen等研究两个周期性亚纯函数分担“2CM+1IM”,得到如下定理.

定理A[6]设f(z)和g(z)是以c为周期的非常数亚纯函数且满足1 ＜μ(f) ≤ρ(f) ＜∞.假设ai(i=1,2,3)为可判别的以c为周期的周期函数且均为f(z)的小函数.若f(z)和g(z) CM 分担a1,a2,IM 分担a3,同时满足

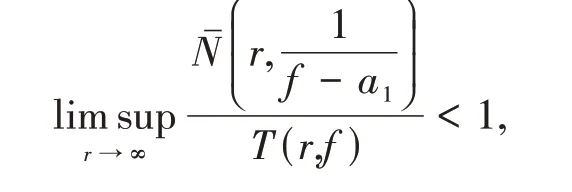
则f(z) ≡g(z).

2020年,Chen等进一步研究f(z)及其n阶差分分担值问题,得到如下定理.

定理B[7]设f(z)是超级严格小于1 的超越整函数且f(z) ≢f(z+c).若f(z)和f(z)CM 分担0 且IM分担1,则f(z) ≡f(z).

同年,Qi等研究f(z)及其n阶差分分担值问题,得到如下定理.

定理C[8]设f(z)是超级严格小于1的超越整函数且a(≠0)为有穷复数.若f(z)和f(z)CM分担0且IM分担a,则f(z) ≡f(z).

在定理B 和定理C 的基础上增加了f(z)是有理函数的情况,将f(z)是超越整函数推广到f(z)是非常数亚纯函数,得到如下定理:

定理1设f(z)为超级小于1 的非常数亚纯函数,c(≠0) ∈C且a(≠0)为有穷复常数.若f(z)和f(z)CM分担0,∞,IM分担a,同时满足Θ(0,f(z)) ＞0,则f(z) ≡f(z).

注1一些想法来自文献[6]和[9].

2 引理

引理1[10-11]设f(z)为非常数亚纯函数,其超级ρ2(f)严格小于1,c(≠0)∈C,为任意常数.则

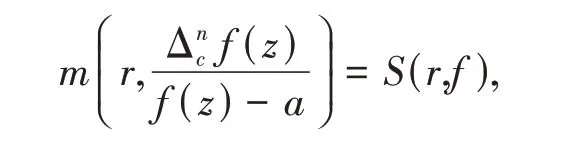
其中r→∞除去一个对数测度有穷的集合.

引理2[2]设f(z)是亚纯函数,若

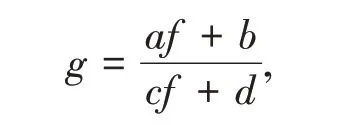
其中a,b,c,d均为f(z)的小函数并且ad-bc≠0,则T(r,g)=T(r,f) +S(r,f).

3 定理1的证明

情形1f(z)为非常数有理函数,可设

结合分担值条件可知存在ε∈(0,1),使得

将式(26)代入式(24)有

这与f(z)是超越的矛盾.

定理1证明完毕.