采用改进神经网络的CORS站高程混沌时间序列分析

张思慧，黄声和

（1.福建船政交通职业学院 土木工程学院，福建 福州 350007；2.福建省特种设备检验研究院，福建 福州 350008）

随着我国IGS（国际卫星全球定位服务）网络不断发展，CORS站（连续运行参考站）的观测数据逐步应用到各个领域.例如，数字中国、地壳运动监测和导航等.但是由于CORS基准站所处的观测环境复杂多变，因此观测到的高程时间序列含有“噪声”.含有“噪声”的高程时间序列在未经处理的情况下，无法满足应用要求.因此对高程时间序列的数据处理显得尤为重要.

目前对于高程时间序列常用的处理方法有：LFS法(最小二乘法)、Spline插值（三次样条插值）和功率谱估计等[1-6].采用以上数据处理方法的前提是所处理的时间序列必须满足Gauss-Markov 条件或正态性(平稳性)条件.然而北京房山观测站所处的环境复杂多变，其得到的观测数据可能无法满足Gauss-Markov 条件或正态性.若不满足上述条件，直接对数据进行拟合、滤波和谱估计等处理，其结果将严重失真.因此，在进行拟合、滤波和谱分析等数据处理之前，必须对数据进行稳定性检验、非线性检验和系统确定性检验.由文献[11]得出北京房山站高程时间序列为部分确定性机制低阶混沌动力系统.

1 数据来源及数据处理流程

采用GAMIT/GLOBK10.35 软件对我国29 个CORS 基准站与国际IGS 基准站进行联合解算，得到北京房山站1999—2009 年单天解算时间序列，作为本文的数据来源.对高程时间序列进行正则化RBF（径向基）神经网络相空间重构，使其满足Gauss-Markov 条件，然后采用小波神经网络对高程时间序列进行滤波分析，对消除“噪声”的数据进行加窗谱估计，然后采用BP 神经网络对北京房山站高程时间序列进行预测，其数据处理流程图如图1所示.

图1 数据处理流程图

2 正则化RBF网络和小波神经网络滤波

2.1 正则化RBF神经网络时间序列重构

依据文献[11]的研究结果可知，在对北京房山站所观测到的数据进行进一步利用前，需要对其进行相空间重构.结合北京房山站高程时间序列的数据特点，本文采用正则化RBF神经网络进行相空间重构[10-15].数据模型选用54个输入神经元、2个隐含层和1个输出神经元.

2.2 小波神经网络滤波

基于房山站数据量和隐节点数，设计正则化RBF 网络的输入层神经元个数为30个，隐层为2个，输出神经元为1个.隐层选取Morlet函数作为小波神经元的激励函数.

2.3 最小差距法

最小差距法能满足拟合误差平方和最小原则，并且在用于拟合不满足Gauss-Markov 条件的线性模型时，仍具有无偏性、最小方差性等良好的统计特性.结合北京房山高程时间序列的特性，本文采用最小差距法对数据进行5阶拟合.拟合所得函数为：

3 谱估计、周期拟合和结果分析

3.1 谱估计

通过正则化RBF 和小波神经网络对北京房山站高程时间序列进行剔除趋势项处理，但其含有的周期项依然存在.为了进一步分析高程时间序列的数据特性，本文结合上述的数据处理结果，采用哈明窗、巴特莱特窗和Parzen窗谱估计进行周期谱估计.时间序列周期谱估计如图2所示.

图2 时间序列加窗谱估计

根据MATLAB12.0的计算结果可知，北京房山站高程时间序列的平均谱功率为7.684×103W.2000—2003 年的年周期为1.003～1.034 a，半年周期为0.438～0.526 a，季周期为0.253～0.347 a；2004—2007 年的年周期为0.994～1.109 a，半年周期为0.478～0.617 a，季周期为0.247～0.378 a.由此可知，北京房山站高程时间序列的年周期性明显，半年周期性和季周期性不是很明显且波动比较大.这是因为受到大陆板块运动、地下水周期性变化、地壳岩浆运动和太阳黑子周期性活动等因素的影响.

3.2 周期拟合

采用快速傅里叶变换方法对北京房山高程时间序列进行周期拟合，结果如下：

3.3 模型计算结果分析

根据上述2.1 和2.2 构建的数学模型，采用MATLAB12.0 软件对北京房山站2000—2006 年观测到的高程时间序列进行滤波和拟合计算，其计算结果如图3所示.

图3 时间序列滤波和拟合

拟合残差和去除趋势FFT周期拟合函数结果如图4所示.

图4 5阶最小差距拟合残差和去除趋势FFT周期拟合

由图3 可知，2000—2001 年北京房山站观测到的数据倾斜趋势波动较大，但是2002—2003 年北京房山站高程时间序列呈现缓慢增长趋势，2004 年甚至出现了负倾斜趋势，2005 年北京房山站高程时间序列急剧增长，这表明这段时间北京房山站所处位置的地壳运动较为剧烈.北京房山站观测数据未能呈现单一的变化趋势，其原因是高程时间序列不是受单一因素的影响，可能受到大陆板块运动、地下水周期性变化和地壳岩浆运动等因素中的两个或多个因素的影响.图4 表明2000—2006 年北京房山站高程时间序列的年周期为0.997～1.037 a，半年周期为0.451～0.629 a，且存在较大波动，季周期为0.232～0.269 a，且有较大波动.由此可知，北京房山站高程时间序列存在明显的年周期性、半年周期性和不明显的季节周期性.

4 BP神经网络时间序列预测

BP网络预测模型只能处理长期记忆性数据，无法精确预测短期记忆性(非平稳)数据.但是经过上述正则化RBF、小波神经网络处理后，北京房山站高程时间序列转化为稳态数据，进而可以进行BP网络预测.

本文的BP 网络选用54 个输入神经元和1 个输出神经元，第一层(隐层)传递函数选用tansig()，第二层(输出层)是单个神经元选用purelin()函数，训练函数选用traingd().BP 网络的学习规则选用负梯度下降函数，其负梯度下降函数[16-17]为

式中：xk、xk+1为节点前后的阈值矩阵权值；ηk为学习速率；gk为当前函数梯度.

1）BP算法模型节点假设三层BP网络，输入节点为xi，隐层节点为yi，输出节点为zi.输入节点与隐层节点间的网络权值为wji，隐层节点与输出节点间的网络权值为vji，θj、θl为阈值.当输出节点的期望值为tl时，隐层节点的输出为

输出节点为

2）误差函数对输出节点求导：

Ek是多个zk的函数，但只有一个zl与vlj有关，各zk间相互独立，则有

3）误差函数对隐层节点求导：

El是多个zl的函数，针对某一个yj，它与所有zl有关，则有

由于权值的修正Δvlj、Δwji正比于误差函数，沿梯度下降，则有

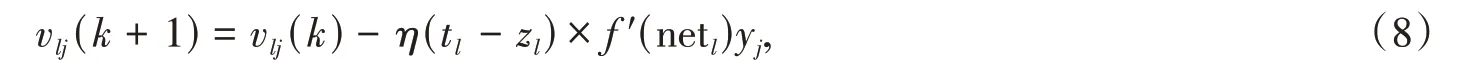
式中：δl为节点误差；η为学习速率.

4）阈值的修正.阈值θ是变化值，误差函数对输出节点阈值求导为

阈值修正为

5）S型传递函数为

6）AR（自回归模型）预测.BP神经网络AR预测数学结构为

式中：y(t)～y(t-na)为时间t的输出；na为节点个数；an为待定参数；e(t)为白噪声输入数据.

将经过模型处理后的高程时间序列代入建好的BP神经网络模型进行预测.2003—2007年高程时间序列预测结果的残差如图5所示.

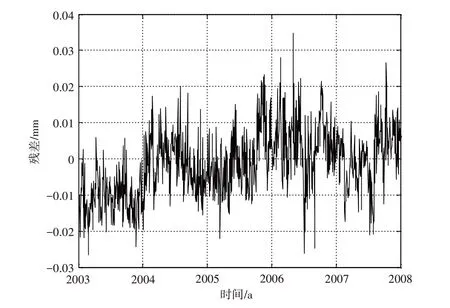
图5 BP网络预测残差图

由图5 可知，构建的BP 网络模型预测残差在0～0.035 m 之间，并且通过计算其相对误差为-0.028 6%～0.040 1%.通过加窗谱估计对BP网络预测的2003—2007年的高程时间序列进行计算.计算结果显示，其存在着年周期性、半年周期性和季周期性，年周期为1.005～1.097 a，半年周期为0.561～0.613 a，季周期为0.389～0.371 a，这与2003—2007年的原始时间序列函数关系基本一致.由此可知，该模型预测精度非常高，BP网络可以很好地对时间系列进行预测.

5 结论

1）基于正则化RBF 对北京高程时间序列进行相空间重构，然后对相空间重构的时间序列进行小波滤波，对滤波后的时间序列进行加窗谱估计.由降噪后的功率谱图可知，北京房山站高程时间序列具有明显的周期性，且具有谐波性.

2）采用BP网络对2003—2007年高程时间序列进行预测.结果显示，其相对误差为-0.028 6%～0.040 1%；采用BP预测2003—2007年的周期性与2003—2007年的原始时间序列函数关系基本一致.预测精度非常高，预测效果良好.