基于机器学习的产品质量在线智能监控方法

徐 钢，黎 敏，吕志民，徐金梧✉

1) 北京科技大学钢铁共性技术协同创新中心，北京 100083 2) 苏州宝联重工有限公司，苏州 215131

钢铁工业是典型的流程工业，产品在制造过程中涉及多个连续衔接的工序.目前，企业对产品质量管控的主要手段是通过制定合理的工艺规范，并采用“事后”抽样检测方式来判定产品的品质.这种依赖于生产经验制订的工艺规范及“事后”抽检的方式容易出现批量的产品质量判废，或导致用户由于质量异议提出索赔和退货.我国钢铁企业每年仅质量判废和质量异议所造成的经济损失近百亿元，如何利用机器学习方法实现产品质量的在线监控、在线优化，制定科学的工艺规范和质量设计，是钢铁企业亟待解决的关键技术.

随着“工业4.0”时代的来临，制造技术正逐步从自动化、数字化、网络化向智能化方向发展.以大数据分析、人工智能、信息物理系统、工业互联网为代表的新一代智能技术已成为企业向绿色化、智能化转型的重要途径[1-3].机器学习作为实现人工智能的重要途径，在人工智能领域的应用引起了广泛的兴趣，如何从海量的高维数据中提取出有价值的信息，并将信息转化为知识是目前机器学习的重要研究方向[4-5].

近年来，机器学习已在不同领域被广泛应用，在材料研发领域，通过高通量计算、高通量表征及高通量数据分析，实现了基于材料基因组的材料数字化研发[6-9]和材料逆向设计[10-12]；在化工和高分子材料领域，通过机器学习方法对分子结构和材料实现精准设计[13-17]；在医药研发领域，采用多变量过程统计分析和机器学习方法，实现药物的快速研发和质量控制[18-20]；在机器视觉和智能识别领域，主要通过深度学习实现人脸、语音、图像、字符等识别、自动驾驶和智能机器人.

机器学习方法在工业领域也有广泛的应用前景，基于多变量的过程统计分析已用于生产过程控制和产品质量在线监测[21-24]，并利用信息物理系统和机器学习方法建立数字孪生模型，实现制造过程的无人化[25-28].目前，这些方法大多应用于离散制造业的智能制造，不仅提高生产效率且实现客户个性化定制[29-31].但由于钢铁生产过程的数据具有多元、强耦合、非线性的特征，因此在利用大数据分析和机器学习方法挖掘数据内在的信息和知识，实现产品质量在线监控还存在一些困难[32-33].

针对钢铁企业在产品质量在线监控中存在的问题，提出基于软超球体算法的质量异常点在线识别和异常原因诊断方法、基于流形学习和邻近点局部投影变换的工艺参数在线优化方法，并利用机器学习方法制定质量设计和工艺规范，提高产品质量的稳定性.这些方法已应用于钢铁企业十余条工业生产线，证实了方法的有效性和准确性.

1 质量在线智能监测与控制方法

实际工业生产中，需要确定不同工序的工艺参数控制范围，即制定不同产品的质量设计和工艺规范.当工艺参数（包括原料参数）在该范围内，认为所设定的过程参数能满足产品质量要求，反之，则可能出现质量异常.目前，钢铁企业在质量设计和工艺规范制定过程中，主要依赖于小批量工业试制和技术人员的生产经验制定对应的规范.如何利用工业大数据分析和机器学习方法来确定产品质量可控区的范围是实现质量在线智能监控的重要手段.

1.1 质量异常点识别方法

多变量统计过程控制 (Multivariate statistical process control, MSPC) 考虑了各变量间的相关性，适用于多元强耦合变量的过程监控[34-36].经典的多变量统计过程控制方法，包括主成分分析（Principal component analysis，PCA)统计控制图、偏最小二乘法(Partial least squares, PLS)统计控制图等.但是，这类多变量统计控制图都有一个假设前提：所有变量满足多变量正态分布(Multivariate normality, MVN)的条件.在这个假设前提下，对于一个稳定的生产过程，正常样本点分布在高维空间中的某个超椭球体内；一旦样本点超出超椭球体的边界，则认为该生产过程出现了异常.超椭球的位置取决于各变量的均值大小和变量间的相关性，而超椭球的大小则取决于变量的方差.

质量异常点识别方法是根据所确定的超椭球边界来判断设定的过程参数是否会造成产品质量异常[37-39].主要方法是通过实际生产数据来确定过程参数可控区的边界，也称为单一类的分类问题.假设给定一个数据集S={x1,x2,···,xn}，其中xi为p维的数据向量，n为样本个数，需确定该数据集的边界，即求解包含该数据集的最小封闭超球体.数据集中的每个样本点与超椭球体中心C的距离均应小于球体的半径R，如图1所示.

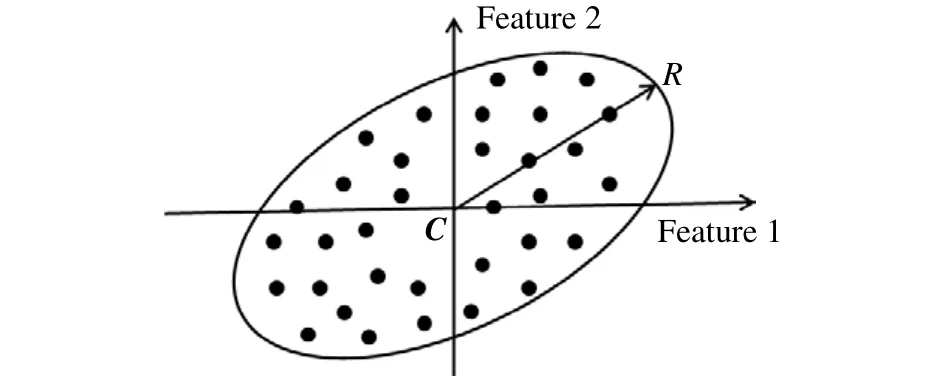
图1 最小封闭超球体示意图Fig.1 Minimum hypersphere diagram

最小封闭超球体可以表述为如下优化问题

在约束条件中加入拉格朗日乘子 αi≥ 0，对应的拉格朗日函数为：

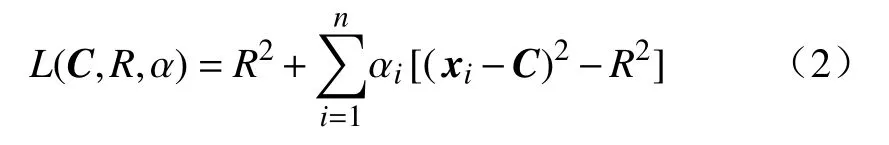
对上式求C和R偏导，且令导数值为0，可求出超球体的优化解：

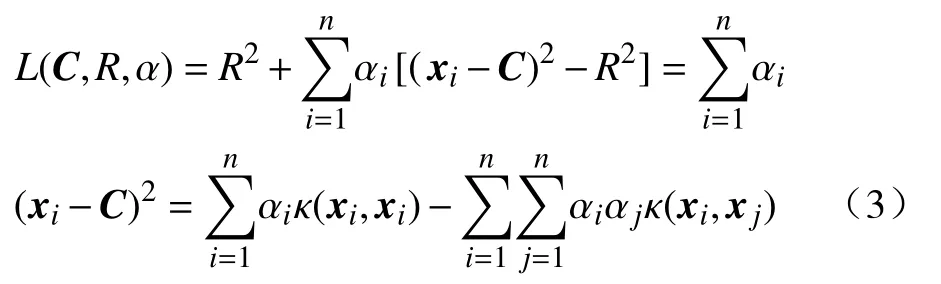
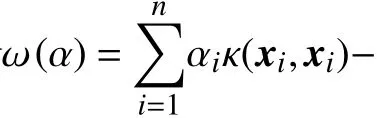
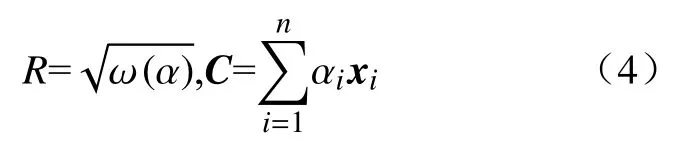
式中，αi是由式（3）求得的最优解.

对待测的检测点x，可以由下式来判断该检测点是否正常.

式中，H(x)表示Heaviside函数.当f(x)=1，则该检测点在超椭球的界外，被判为异常点.

但实际生产数据中，过程参数间往往存在多重耦合，变量间有着复杂的非线性特征，因此过程参数间并不满足多变量正态分布的假设前提.当数据集中存在非线性、非正态分布时，这种线性形式的超椭球边界易造成误判，如图2所示.

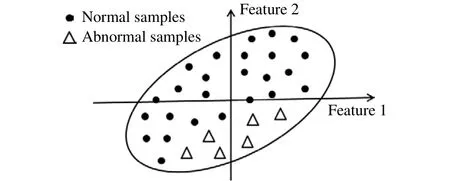
图2 线性超椭球将异常点判为正常点Fig.2 Abnormal samples misjudged as normal samples in the linear hypersphere

近来年，基于核函数的非线性模式分析方法受到关注，核方法通过非线性核函数来表示数据内在的复杂结构特征，用于确定非线性软超球体的边界[40-41].非线性核函数将原始欧氏空间上的数据集映射到高维特征空间中，通过映射点ϕ(x)和ϕ(z)的内积（对偶形式）求解非线性情况下的封闭超球体，如图3所示.从图3中可以看出，原始空间的样本点（左图）分布在一个复杂的封闭体内，而通过非线性核函数变換后，原先的样本点x映射到特征空间中的点ϕ(x)分布在封闭的球体内（右图）.

图3 样本点从原始空间映射到特征空间Fig.3 Samples mapped from the original space into the feature space

通过非线性核函数将原始空间中的样本点映射到特征空间后，可按照式（1）的方式，建立特征空间中封闭超球体的优化解.

式中，常数项A和松弛因子 ξ的乘积项表示允许个别正常样本被判为异常的比例，比如，允许2%的正常样本被划分在超球体外，比例可根据用户对产品质量保证值的要求动态设定.设定松弛项是为了更严格地控制产品质量的可靠性，比例的选择与第一类错误和第二类错误有关[33].经非线性核函数映射后，拉格朗日函数为

式（7）与式（3）不同之处在于，式（3）是采用线性函数，因而只能解决简单边界问题，即超椭球边界，而式（7）采用非线性核函数解决复杂非线性边界问题.两者差别主要是选择线性函数还是非线性核函数，而求解的过程与上述所讨论的方法基本一致.

在求解式（7）拉格朗日函数的优化解过程中，可以发现大部分αi等于0，只有少部分位于超球体边界的样本αi大于0，这些样本点称为支持向量（Support vector）.因此，在异常点的识别时只需考虑少数支持向量对应的样本点xi和αi，这样大大简化了异常点的识别过程，使得在线识别系统能够满足实时性要求.式（8）给出了基于支持向量的非线性封闭超球体异常点检测方法

式中，x表示待测点，q为支持向量的个数，γ表示松弛系数，表示支持向量，表示支持向量对应的权重系数.实际上，在判别式（8）中，D是学习样本在训练阶段求得的常量，并不需要在线计算，而κ(x,x)根据核函数的定义也是一个常数.与待检测点x有关的项只有因此，一个待识别样本在线判别时仅需计算式（9），并由式(8)来判定质量是否异常，计算时间仅需几毫秒，完全满足质量在线监测的实时性要求.

1.2 质量异常原因诊断方法

在工业应用中，一旦发现设定的工艺参数已偏离超球体时，应及时、准确地诊断出哪些工序、哪些工艺参数是造成偏差的原因，以便后续生产中调整工艺参数，避免出现批量的质量异常.质量异常诊断模型的功能是，从设定的工艺参数中寻找引起偏离可控区边界各工艺参数的贡献值，贡献值大的工艺参数是偏离可控区的主要原因.

待检测样本x到非线性超球体（软超球体，Soft hypersphere）球心的距离平方

由式(9)可知，造成R2(x)变大的原因是上式右边第二项.若采用高斯核函数，则有

因而，待测样本x的第j变量对偏离的贡献值为

为了消除变量量纲对贡献值的影响，需对上式做标准化处理，标准化后变量j对偏离的贡献值

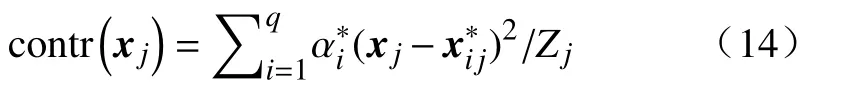
式中，Zj为变量j的方差，contr(xj)中贡献值最大的那些变量是造成质量偏离的主要原因.异常点识别和异常原因诊断方法的工业应用实例将在下面章节中讨论.

1.3 工艺参数在线调整方法

在确定导致质量异常原因后，需要对工艺参数进行在线调整，使生产过程回归到正常状态.常用的多变量优化算法包括神经元网络、深度学习、粒子群算法.这些算法大多采用正向推理方式，通过迭代找出优化解，但这会影响控制系统的实时性.因此，在实际工业应用中，需要研究多变量、非线性情况下工艺参数的快速优化算法.为了解决工艺参数在线动态优化问题，提出基于流形学习的过程控制参数优化方法.

产品在制造过程中涉及多个连续衔接的工序，不同工序须严格控制工艺参数才能生产出合格的产品，如钢材在制造过程中涉及冶炼（控制成分、夹杂物）、连铸（控制铸坯组织）、成形（控制形状、尺寸、组织）和热处理（主要组织和材料性能）等工序的质量指标控制.工序间的质量指标存在遗传性和关联性，且与各工序设定的工艺参数密切相关.如何从高维、强耦合、非线性复杂数据中，提取低维数据空间拓扑结构的机器学习方法—流形学习，近年来引起了广泛关注.主流形学习可以理解为，从实际生产数据中提取出工艺参数随质量指标变化的流向“管道”，在“管道”内的工艺参数可以满足质量要求.

流形是定义在一个拓扑空间上的某个子集，它建立在欧氏空间（原始空间）中，且与欧氏空间是微分同胚的.如果数据集X中任意两个不同的样本点a、b，都存在a邻域U及b邻域V，使得V∩U=V∪U=Θ，称 (X,τ)为Hausdorff拓扑空间.τ表示X的子集所组成的一个非空集合，且满足：τ中元素的并集仍属于τ，其有限交集及空集 Θ和X都属于τ，并称τ为X的一个拓扑结构.流形学习包括无监督和有监督数据的流形学习[42-45].无监督流形学习是解决高维数据的低维主流形提取方法，主要用高维数据的降维和消噪；有监督流形学习是根据标签数据变化规律，提取数据随标签值变化的低维主流形的结构，比如，工艺参数随质量指标的流向.

给定高维的观测数据集X={x1,x2,···xn},xi∈RD为独立同分布随机样本，分布在光滑的d维流形上，即在D维欧氏空间中嵌入d维流形，其中d≤D.流形学习就是从观测数据集X中寻找低维的嵌入映射，从而求得微分同胚的低维主流形.在建立观测点xi局部邻域的流形时，需要从数据集中抽取与该观测点邻近（或相似）的数据点构建邻近（相似）矩阵，并计算矩阵的特征向量，通过选择若干最大特征值对应的特征向量作为主向量，且将数据投影到主向量上得到低维的嵌入映射，即主流形.

在实际工业应用中，高维数据中内在的低维主流形常常是未知的.流形学习的目的是从数据集中，通过嵌入局部邻域的低维主流形来描述整体的流形结构，在不丢失数据内在的本质特征情况下，消除数据的次要因素和随机噪声，提取出数据低维的本质结构—主流形，图4给出流形学习的示意图.

图4 图4 流形学习示意图Fig.4 Manifold learning diagram

流形学习过程包括3个步骤：

（1）首先，对样本集进行标准化处理，消除变量的不同量纲在计算几何距离时影响，并建立标签样本集{(x1,Si),(x2,Si),···(xi,Sj)···(xn,Sp)}，式中Sj表示标签样本的状态，即样本在流形空间中位置.

（2）搜索距样本点xi邻近且与其处于同类状态的邻近点子集{Si(Vi)}，同时选择与xi相邻，但处于下一个状态的邻近点子集{Si+1(Ui)}.

（3）对所有n个样本点建立邻近点集矩阵{N1,N2,···,Nn}作为最终的邻近矩阵，其中子矩阵Ni的维数为ki×D，ki为观测点xi邻近点个数，D为样本空间维度.

对每个子矩阵Ni求得协方差矩阵，再对协方差矩阵进行特征值分解，求得特征值Ui及对应的特征向量λi

最大的特征值所对应的特征向量表示流形在xi局部区域的主流形.由于特征向量相互正交，主流形构成了局部区域的切空间.主流形的提取实现了高维流形向低维主流形的转换，揭示了流形在局部区域的主要变化趋势（在图4中由箭头表示），并消除数据中的随机噪声和非主流的变化因素.将邻域矩阵Ni投影到局部区域的切空间Ti

式中，向量Ti表示低维主流形演化方向，为由式（15）求得的d个最大特征值的特征向量.

对每个观测点邻近矩阵分别计算特征向量，可以构建演化矩阵T=[T1,T2,···,Tn].演化矩阵的每个向量Ti表示流形在局部区域进行线性化处理后演化方向，因此演化矩阵T仍可描述非线性流形结构，这个方法也称为局部线性化.

在实际工业应用中，除了需掌握流形变化趋势外，还应确定质量优化与调整过程中各工艺参数的调节量.工艺参数的调节量

ΔB可以理解为当观测点偏离主流形时参数的偏移量.由于向量ΔB是经过标准化处理，因此需要对每个变量进行反标准化计算.

基于流形学习的过程控制参数优化方法的优势是，通过机器学习已提取出工艺参数与质量指标间对应的主流形，掌控工艺参数随质量指标的流向，因此在工艺参数调整时更具针对性和实时性.基于流形学习的工艺参数在线调整方法的工业应用实例将在下面章节中讨论.

1.4 工艺规范的设定方法

由于工艺参数间存在多重耦合和非正态分布的数据结构，数据在高维空间中的分布通常是一个软超球体，如果凭借目前企业常用的基于参数独立同分布假设的6σ方法，设定的工艺规范必将造成产品质量的偏差.正确预设定工艺参数的方法应从软超球体中寻找最大内接矩形体（或平行体），最终根据最大内接矩形体来确定工艺参数的设定范围.

产品制造过程涉及不同工序，每个工序需设定关键质量指标和工艺参数控制范围，才能确保最终产品的质量.设工序1的关键工艺参数为A1、A2···，工序2关键工艺参数为B1、B2···，最终工序的工艺参数为C1、C2···Cm，所有工序总计有p维变量.工艺参数的上、下限可以表示为

式（19）可以解释为，寻求每个工艺参数在软超球体内最大区间，同时需满足其他工艺参数的区间范围，即寻求最大的并集，具体应用实例将在下章节中讨论.

在实际工业应用中，请注意下面几个问题：

（1）关键变量的选择.

流程工业在产品制造过程中涉及多个连续相关的工序，工艺参数较多，应将那些与产品质量密切相关的质量指标和工艺参数作为关键变量.在遴选过程中，可以通过互相关分析来判定工艺参数与产品质量的关联度，并选择相关系数绝对值大的工艺参数作为工艺规范需优化的关键变量.

（2）相关变量的选择.

实际工业生产中，工艺参数间常出现强耦合的情况，软超球体会随相关系数的大小出现倾斜，最大内接矩形体同样也会倾斜（请参看图9）.因此，当两个工艺参数间存在强耦合时，原则上选择其中一项关键工艺参数的边界来确定关键变量上、下限，另一项关键工艺参数用来修正由前一项工艺参数确定的范围是否合理.

（3）组合优化问题.

根据集合理论，寻求软超球体中最大的内接矩形体是一个最大集合和最小集合的组合优化问题.通过将软超球体投影到二维平面上寻求最大的内接矩形，并将所有从二维投影所求得的内接矩形边界来获得所有变量的最小集合（并集），即软超球体的最大内接矩形体.因此，对于复杂边界的软超球体，组合优化过程需在全域寻求优化解.

（4）工艺规范验证.

数据的可靠性和完备性对分析结果有着重大影响，应验证数据的可靠性，确保数据准确、可靠；此外，还需验证数据的完备性，应考虑训练数据是否涵盖了所有区域，尤其是收集出现质量异常的区域.通常包含一定数量异常点的训练数据集更有利于准确地划分软超球体的边界.

2 工业应用实例

钢铁企业需根据客户要求，在生产过程对各工序的工艺参数在线智能监控，确保产品的最终质量.下面以汽车用钢为例，讨论运用机器学习方法在产品质量在线监控、在线优化和在线预设定中的工业应用实例.

深冲钢（IF钢）是汽车构件的重要原材料，在成形与使用中需考虑其冲压性能、力学强度、抗冲击性能等质量要求，主要性能指标包括：抗拉强度、屈服强度、延伸率、塑性应变比等.深冲钢生产过程中涉及炼钢、热轧和热处理等工序，不同工序需严格控制相应的工艺参数才能制造出客户要求的质量指标.炼钢工序应控制冶炼过程中钢材中主要成分：C、Mn、P、S等元素的质量分数；热轧工序：加热炉出口温度、精轧入口温度、精轧出口温度、卷取温度等；热处理工序：均热平均温度、快冷出口温度、时效出口温度、缓冷出口温度等.

从实际生产线上采集不同牌号深冲钢的工艺参数和质量指标值.原始数据集中有24个工艺参数，其中12个工艺参数与产品的几何尺寸有关，而与材料性能无直接关系，因此选择12个相关的参数作为数据学习的样本集，主要成分和工艺参数名称及统计量如表1所示.

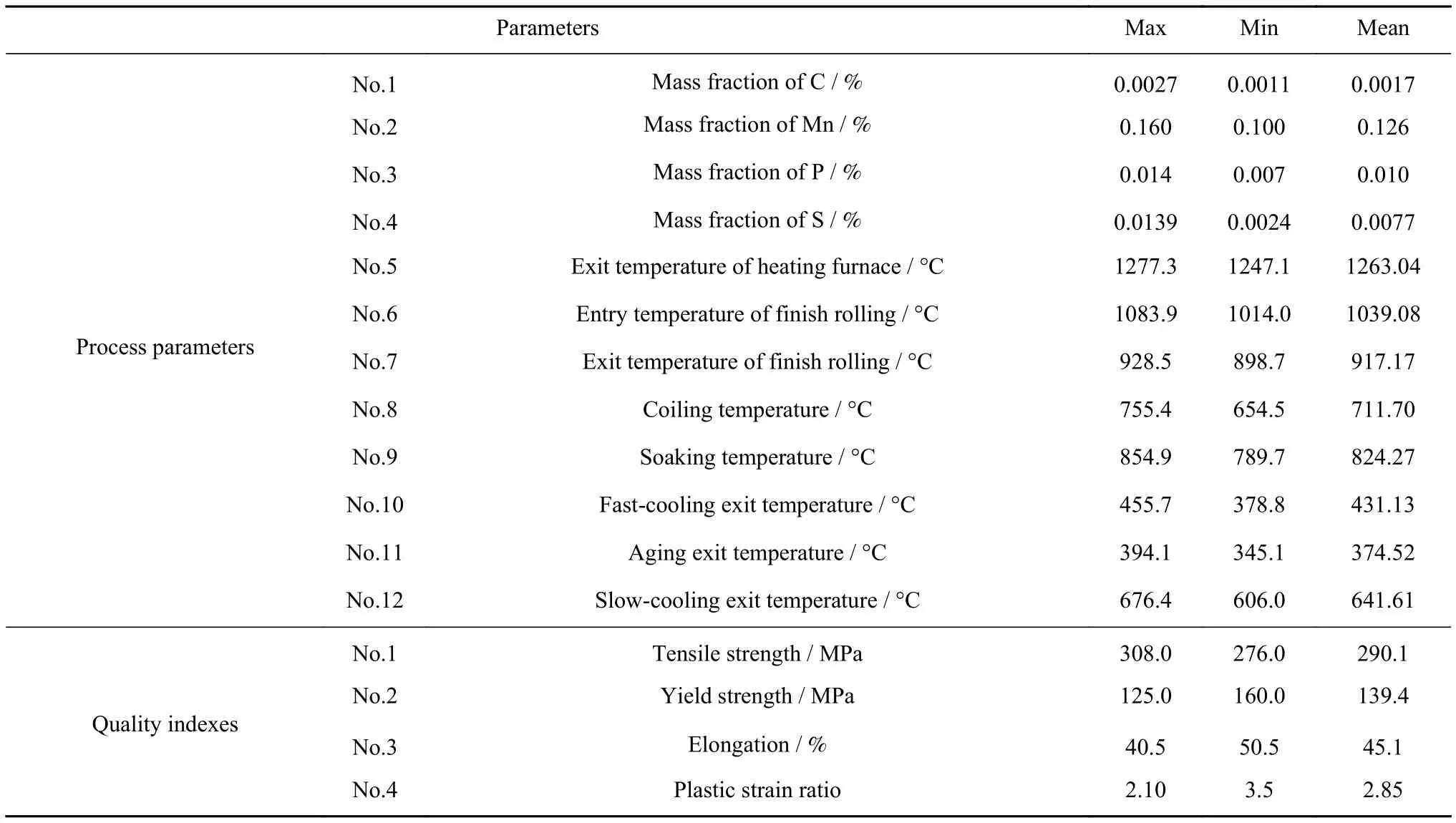
表1 关键工艺参数、质量指标及统计量Table 1 Key process parameters, quality indexes, and statistics

2.1 质量在线监测与诊断

从采集的数据集中随机选取160个样本作为训练样本，并设松弛系数 γ= 0.02，由式（4）确定的软超球体R2值作为控制限，训练结果如图5(a)所示.从图中可以看到，绝大部分样本均在控制限以下，这些样本都在软超球体的内部（正常样本），但有3个样本在控制限的边界或超出控制限，可能存在质量异常的情况.查看原始数据后发现，除第46样本的质量指标略超出标准外，第28、58样本处在正常范围，但接近临界值.出现这种情况的原因是，在训练阶段设定松弛系数 γ= 0.02，即允许个别正常样本被判为异常（在软超球体边界外）.松弛系数会影响软超球体R2值，因此对质量要求高的产品，为了严格监控生产过程可以适度降低控制限R2值.

图5 训练集的控制限R2(a)和在线监测结果(b)Fig.5 Control limit R2 (a) of the training set and online monitoring result (b)

经过训练后的软超球体模型中，有36个支持向量，这些支持向量及对应的权重系数通过式（8）对产品质量进行在线监测.从生产线上另采集120个样本数据来验证方法的有效性，在线监测结果如图5(b)所示.从图5(b)中可以发现，第25号样本点已超出了控制限，说明工艺参数出现异常；第57号样本点临近控制限，也可能出现异常.为了查找异常的原因，利用式（14）计算样本点工艺参数的贡献值（图6(a)和6(b)），发现碳质量分数（表1中序号1）和热轧加热炉出口温度（表1中序号5）贡献值最大.通过在线监控系统的数据显示，25号样本点的碳质量分数为0.0029%，已超出了0.0027%最大值，加热炉出口温度为1249 °C，接近最小值1247 °C；57号样本点的碳质量分数为0.0027%，加热炉出口温度为1247 °C，均为临界值，其他工艺参数均在控制限范围.查看样本点的质量指标后，发现第25样本点的抗拉强度仅为275 MPa，已低于表1中给出的276 MPa最小值；第57样本点的屈服强度为160 MPa，是表1中给出的最大值.

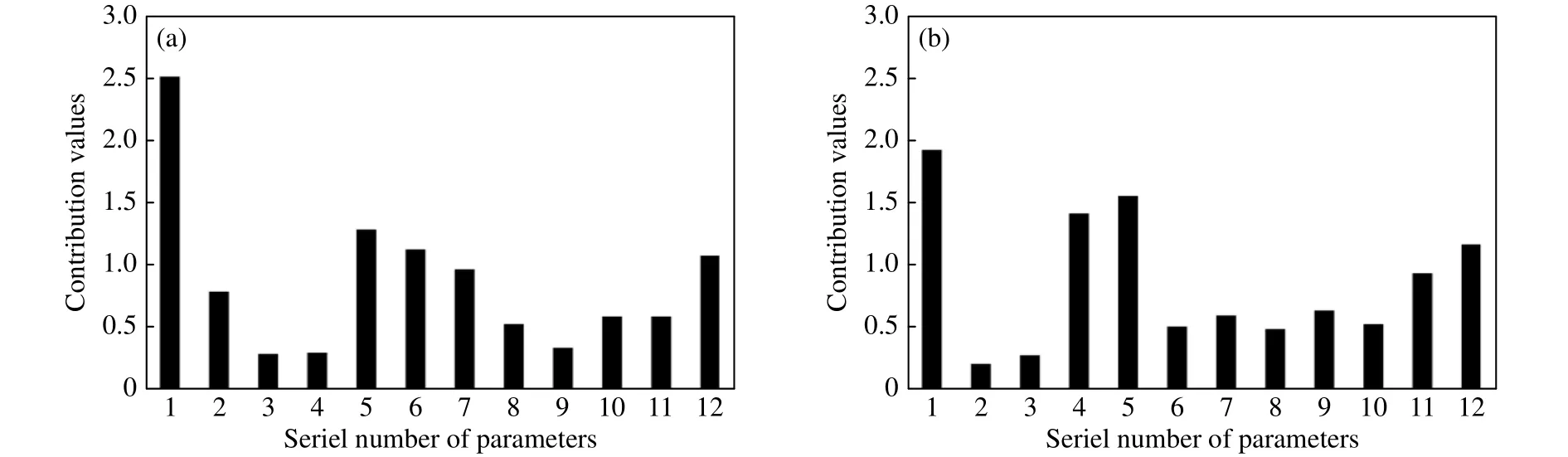
图6 工艺参数(参数序号在表1中)的贡献图.(a)第25样本;(b)第57样本Fig.6 Contribution chart of parameters: (a) sample No.25; (b) sample No.57 (serial numbers of the parameters are listed in Table 1)

由于工艺参数与质量指标间有着密切的关联，因此可以通过工艺参数的在线监测和诊断实现产品质量在线监控.利用机器学习提取数据中内在的信息和知识，本质上是建立实体对象（工艺装备和产品）与数字对象（工艺参数和产品质量）之间的数字孪生模型，并通过孪生模型来预测在设定的工艺参数条件下实体对象的行为.通过上述工业应用案例分析，证实采用软超球体方法所确定的控制限能有效地实现质量在线监控，并快捷、准确地诊断出现异常原因.

2.2 质量设计与在线优化

为了分析各工序中主要工艺参数随质量指标的变化趋势，从IF钢不同等级的主要工艺参数和质量指标数据中分析主流形的形态.钢的屈服强度是衡量IF钢性能的重要质量指标，所采集的IF钢的屈服强度范围分布在155～130 MPa之间.为了便于分析，将样本集的屈服強度按5 MPa作为一个级差，分成5个等级.按照式（16）给出的主流形学习方法，分别从相邻等级中寻找邻近点，邻近点个数设定为20，计算各工艺参数局部低维主流形的演化方向.为了便于讨论，仅给出与屈服强度密切相关的碳、锰成分、热轧精轧入口温度、热处理均热出口温度的主流形演化规律，如图7所示.

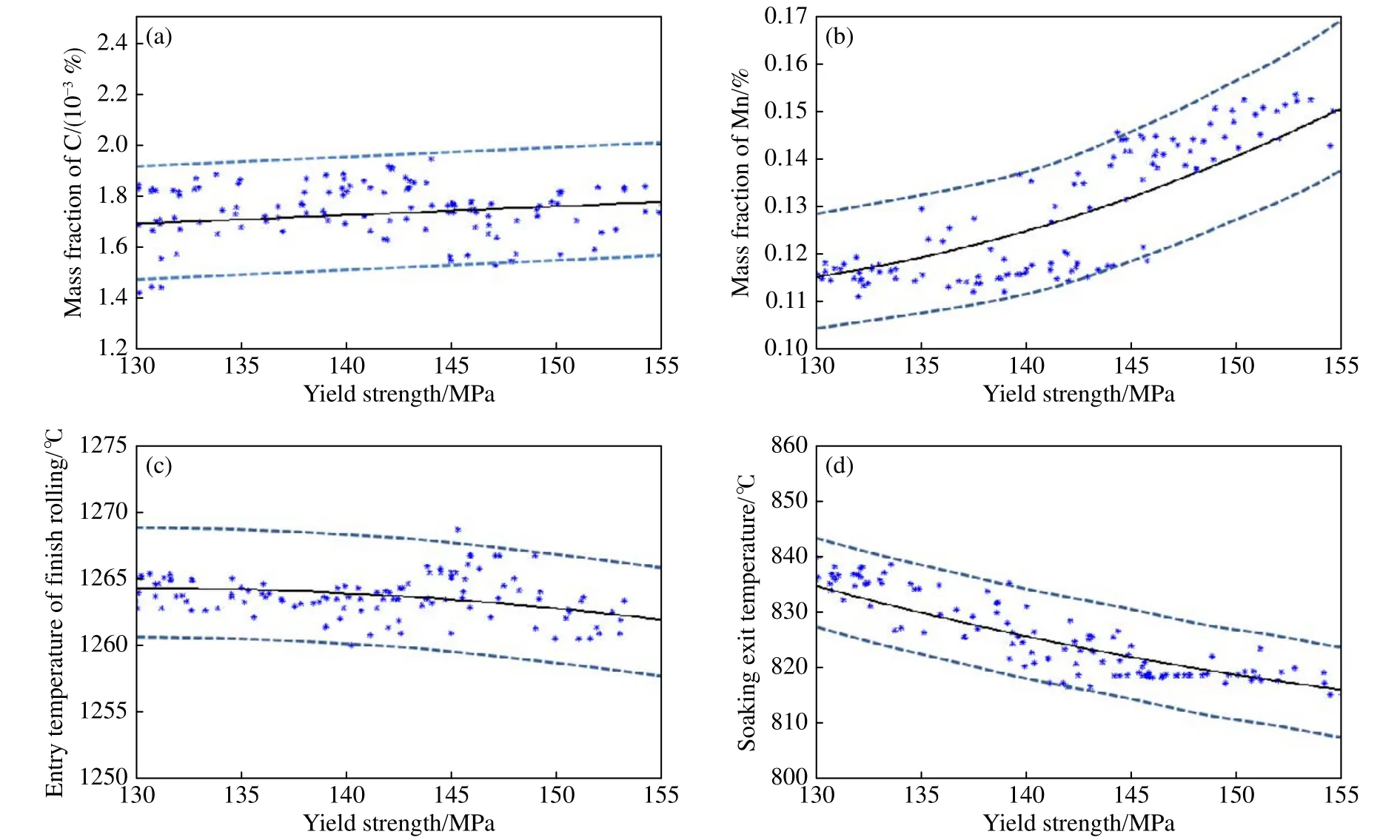
图7 工艺参数与屈服强度的主流形.(a)碳含量流形;(b)锰含量流形;(c)精轧入口温度流形;(d)均热温度流形Fig.7 Main manifold between the process parameters and yield strength: (a) manifold of C; (b) manifold of Mn; (c) manifold of the entry temperature of finish rolling; (d) manifold of the soaking temperature

从图中可以看出，主流形分布在“管道（虚线部分）”内，其中碳（图7(a)）和锰成分（图7(b)）在屈服强度为130 MPa（DC06系列）的产品中质量分数较低，而屈服强度为155 MPa（DC04系列）材料的质量分数较高；热轧精轧入口温度（图7(c)）、热处理均热出口温度(图7(d))对于屈服强度为130 MPa的材料来说较高，而对于屈服强度为155 MPa的材料呈下降趋势.

由式（16）确定的关键工艺参数的主流形管道还可用来制定按用户个性化需求的质量设计，表2给出了不同屈服强度的工艺参数范围.由于质量指标中，抗拉强度、延伸率、塑性应变比等指标在实际工业生产中基本上能满足产品质量要求，而屈服强度关系到IF钢的成形性能，且在生产过程中较难精准控制，因此表2中仅给出针对屈服强度的质量设计.其他质量指标同样可以按用户要求制定相应的工艺参数范围，并与按屈服强度制定的工艺参数进行优化组合，最终确定工艺参数值以满足用户个性化定制.

表2 屈服强度的质量设计Table 2 Quality design of the yield strength

另外，局部主流形演化算法还可用于产品质量在线优化，如果前工序的工艺参数出现偏差时，需要在后续工序中对工艺参数作动态调整，纠正前工序造成的质量偏差.以前面讨论的第25号样本点为例，该点的碳质量分数为0.0029%，Mn的质量分数为0.13%，P为0.009%，S为0.012%，C含量已超出了工艺规范要求的最大值，因此，需要在轧钢和热处理工序对温度参数作适应的调整.从数据集中搜索与这4个成分参数邻近的20个历史样本点，组成邻近矩阵N.由式(15)求出协方差矩阵的特征矢量，并从中选择前5个最大特征值所对应的特征矢量组成的局部低维主流形的演化方向矩阵T.由式(16)和式(17)求出主流形矢量以及后续工序的工艺参数的调整量.表3 给出了实际调整量以及调整后的工艺参数.对后续工序的工艺参数作了调整后，发现材料性能有了明显的改善，塑性应变比由原来的2.3 提高到2.9，屈服强度从160 MPa 调整到140 MPa.通过这个工业应用实例，证实了局部主流形算法能有效地实现产品质量在线优化.

表3 第25号样本点的工艺参数调整值Table 3 Adjustment of process parameters for sample No.25

2.3 工艺规范的预设定

下面以IF大类钢种为例，讨论如何通过寻求软超球体中最大的内接矩形体的方法来制定IF钢各工序的工艺规范.首先，需对获取的数据进行清洗，清洗的目的是剔除数据中的异常点和强耦合的过程变量.热处理序是IF钢制造过程最后一道关键工序，工艺参数的设定将决定材料最终的性能，其主要工艺参数包括：均热平均温度、快冷出口温度、时效出口温度、缓冷出口温度等.工艺参数间的相关系数已在表4中给出，有4对变量的相关系数小于0.5，因而只讨论这4种情况下软超球体在二维投影中的上、下限.图8给出了热处理工序中，这4对变量的上、下限.

表4 热处理工艺参数的相关系数Table 4 Correlation coefficient of the process parameters in the heat treatment

在图8(a)中，最大内接矩形的上、下限：均热温度 840～814 °C，快冷温度 456～396 °C；图8(b)中，均热温度 840～807 °C，时效温度 392～356 °C；图8(c)中，均热温度839～ 809 °C，缓冷温度662～618 °C；图8(d)中，时效温度 392～357 °C，缓冷温度 662～620 °C.根据式（17）的要求，寻求所有变量的最小集合（并集），热处理工序的工艺参数的上、下限：均热温度839～814 °C、快冷温度456～396 °C、时效温度 392～357 °C、缓冷温度662～620 °C.

图8 热处理工序的工艺参数上、下限.(a)均热温度与快冷温度;(b)均热温设与时效温度;(c)均热温度与缓冷温度;(d)时效温度与缓冷温度Fig.8 Up and low limits of the process parameters in the heat treatment: (a) soaking and fast-cooling temperature; (b) soaking and aging temperature; (c)soaking and slow-cooling temperature; (d) aging and slow-cooling temperature

由于时效温度和快冷温度存在强耦合（相关系数为0.72），因而需讨论强耦合情况下关联工艺参数的边界问题.软超球体在时效温度、快冷温度二维变量上的投影如图9所示，从图上可发现二维投影是一个倾斜的复杂边界（倾角为相关系数的正切函数），这时最大内接矩形变成了平行四边形，上、下限需从A、B两点的边界来确定.平行体的边界：时效温度396～347 °C、快冷温度451～398 °C；而由最大内接矩形确定的上、下限：时效温度 392～357 °C、快冷温度 456～396 °C，求两个集合的并集，最终的上、下限：时效温度392～357 °C、快冷温度 451～398 °C.

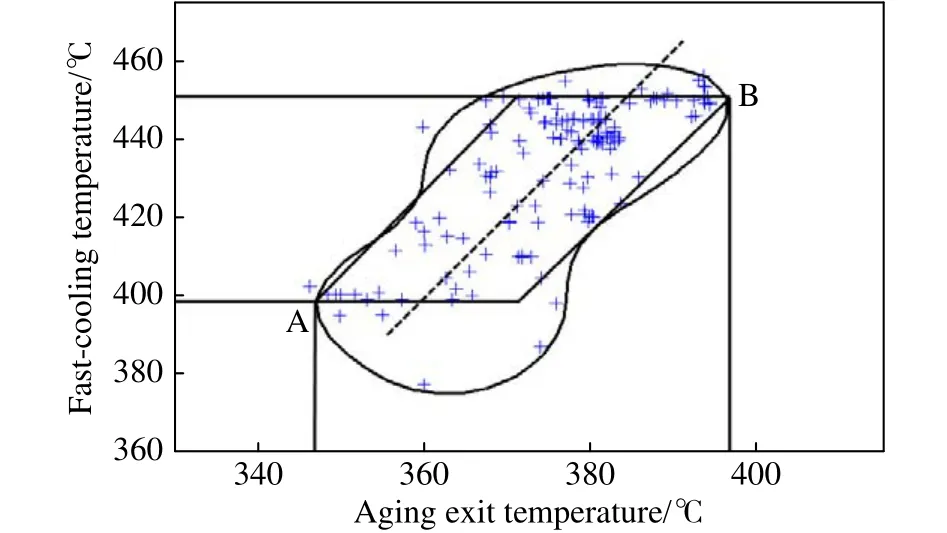
图9 时效温度与快冷温度的上、下限Fig.9 Up and low limits of the aging temperature and fast-cooling temperature

参照同样的方法，确定其他工序的工艺参数的上、下限，表5给出各工序工艺参数的设定范围.为了对比不同方法所确定的上、下限差异，表5中还给出了由最大最小值和6σ方法确定的上、下限.可以看出，采用软超球体边界所确定工艺参数的上、下限区域比其他方法所确定的上、下限区域要严格，且更加合理和精准.

3 讨论和建议

在实际工业应用中，下面几个问题需进一步讨论：

（1）由于流程工业的过程控制参数之间往往存在多重耦合，数据集中不可避免地存在非线性问题.在确定超软球体的边界时，通常采用高斯非线性核函数，还可以采用其他非线性核函数.当选用高斯核函数时，核参数σ的选择非常重要，取值过大或过小都可能造成软超球体边界的改变并导致产品质量误判，同时也会影响到支持向量的个数.当核参数σ取值较大时，高次项会迅速衰减，软超球体退化为超椭球体，会造成异常点被判为正常样本.当核参数σ取值较小时，高次项的影响将更加突出，但容易造成软超球体边界过拟合，不仅增加支持向量个数，影响在线监测系统的实时性，同时会影响软超球体最大内接矩形体的确定.图10给出了σ取不同值时，二维软超球体的边界，当σ=70，超球体边界实际上是椭圆，覆盖的区域较大，但易发生第二类错误，即将异常样本判为正常样本；当σ=25，超球体边界是个紧凑的封闭区域，绝大多数正常样本点分布在封闭区域内，且准确的划分了正常样本与异常样本的边界.

图10 σ取不同值时,软超球体的边界Fig.10 Border of the soft hypersphere with different σ values

（2）基于软超球体的工艺规范制定与基于主流形的质量设计都是围绕如何设定工艺参数范围，从表2和表5中可以发现，工艺参数的范围大部分是重叠的.两者不同之处在于：（a）工艺规范是根据大类钢种数据的质量可控区边界（软超球体的最大内接矩形）来确定工艺参数范围，因此参数范围要比质量设计给出的范围宽泛一些；（b）质量设计是根据小类钢种数据，即按照质量指标的区段，通过计算工艺参数随质量指标变化的主流形“管道”来确定单一工艺参数范围，可根据客户对质量指标的具体要求实现精准定制，适用于钢种性能的局部调整；（c）软超球体的边界是根据所有过程参数的数据结构特征，综合考虑了多变量、强耦合、非线性等复杂情况下确定的质量可控区边界，所制定的工艺规范更符合实际情况；而主流形是针对单一工艺参数的局部区域内“管道”边界来制定质量设计，两者即有相似之处也有差别，在实际应用中可互相对照来制定工艺规范和质量设计标准.

表5 工艺参数的预设值Table 5 Preinstalling values of process parameters

（3）从概念上讲，工艺规范制定过程是从软超球体中寻求最大的内接矩形体，但在实际工业应用还应考虑所制定的工艺规范是否具有可行性.在工艺参数预设定时，应考虑以下几个问题：（a）工艺装备条件：由于工艺装备的过程能力决定了工艺规范可操控的范围，因而在工艺参数预设定时，应综合考虑工艺装备状况、工艺流程的优化、工艺参数可控范围和控制精度等因素；（b）数据采集范围：工艺规范制定是基于数据驱动的机器学习方法，因此数据的可靠性和完备性对机器学习结果有着重大影响.训练数据集应验证其可靠性，确保数据准确、可靠，还需验证数据的完备性，包括采集所有关键变量数据和质量异常数据.包含一定数量异常点的训练数据集更有利于准确地划分软超球体的边界，因而有利于正确地制定工艺规范.

4 结论

本文结合钢铁制造流程的特点，分析讨论了机器学习方法在产品质量在线监控、在线诊断、在线优化和在线预设定中的应用实例，证实了利用机器学习提取数据中各种信息和知识，可以实现产品质量实时在线监控，避免由于用户质量异议和批量判废造成重大经济损失.主要结论如下：

（1）针对工业生产数据具有高维、强耦合、非线性的特点，提出基于软超球体算法的产品质量异常在线识别和异常原因诊断方法.采用非线性高斯核函数将原始空间的样本点映射到高维特征空间，通过求解特征空间中软超球体边界来确定质量控制限，并利用支持向量和异常点的贡献图实现产品质量在线监测和异常原因在线诊断.

（2）为了满足产品个性化定制的需求，提出基于机器学习的质量设计和工艺规范制定方法.通过多类邻域的主流形学习方法确定各工艺参数随质量指标变化的局域主流形，并由主流形所形成的质量可控区的局部区间范围来制定个性化的质量设计；提出通过寻找软超球体最大内接矩形来制定工艺规范的方法，并讨论了多重耦合情况下工艺规范制定和规范验证等相关问题.

（3）通过汽车用钢（IF钢）生产数据分析，讨论了机器学习方法在质量在线监控、在线诊断、在线优化的应用实例和相关的问题.这些机器学习方法已在十余条生产线推广应用，证实了方法的有效性和实时性，质量在线判定的准确率达到99.2%，在线监控系统对每个产品在线检测所需时间不到0.1 s，满足产品质量在线监控实时性要求.