全固废膏体关键性能指标的多目标优化
2022-04-07阮竹恩吴爱祥王贻明王少勇王建栋
阮竹恩,吴爱祥,王贻明,王少勇,王建栋
1) 北京科技大学土木与资源工程学院,北京 100083 2) 北京科技大学顺德研究生院,佛山 528399 3) 北京科技大学金属矿山高效开采与安全教育部重点实验室,北京 100083
全尾砂膏体充填技术因其安全、环保、经济、高效的优点已经广泛应用于国内外多座矿山,在尾矿处置、采空区治理等方面取得了较好的效果[1-2].在全尾砂膏体充填工艺过程中,来自选厂的低浓度全尾砂料浆通过深锥浓密机进行深度脱水获得高浓度的底流,再与水泥搅拌制备成不分层、不离析、不脱水的膏体料浆,最后通过管道输送至井下采空区进行充填,实现了“一废治两害”,即利用全尾砂这一固体废弃物治理了采空区垮塌和尾矿库溃坝两大灾害.我国学者围绕全尾砂浓密[3-5]、膏体搅拌制备[6-8]、膏体管道输送[9-12]以及采场充填体力学性能[13-16]等方面进行了广泛而深入的研究,取得了很好的研究成果,促进了全尾砂膏体充填技术的发展与应用.
据《中国矿产资源节约与综合利用报告(2015)》[17]显示,我国废石堆存438亿吨,约为堆存尾矿的3倍,同样造成了严重的安全与环境问题.近年来开始将废石以粗骨料的形式加入到全尾砂膏体中,再进行采空区充填[18-19].为此,学者们围绕废石添加对膏体充填的影响进行了研究.分析了废石对膏体输送性能[20]、抗离析性能[21]和充填体力学特性[22]的影响,发现添加废石有利于提高充填体的稳定性和降低充填成本.同时,以高炉水淬渣为原料的胶固粉也被广泛应用于矿山充填中,胶固粉与水泥相比在离析、泌水率、早凝早强等方面具有较好的性能[23].
为此,本文在全尾砂膏体充填的基础上,结合国内外研究现状,提出全固废膏体充填,即应用矿山的全尾砂、废石、水淬渣等全部固体废弃物进行膏体充填,将矿山的废石作为粗骨料添加到全尾砂料浆中,并应用胶固粉代替水泥,实现“全废治三害”.全废是指矿山全固废,三害是指采空区垮塌、尾矿库溃坝和废石场滑坡.结合国家标准《全尾砂膏体充填技术规范》[24]中对膏体充填关键技术指标范围的规定,应用正交设计重点研究固体质量分数、废石掺量和胶固粉耗量对全固废膏体的塌落度、屈服应力、单轴抗压强度和泌水率的影响,再应用总评归一值模型进行全固废膏体关键性能指标的多参数多目标优化.
1 实验材料与方案
1.1 实验材料
本文实验所用全尾砂和废石来源于某铅锌矿,用以水淬渣为原料制备的胶固粉作为胶凝材料.
全尾砂、废石和胶固粉的密度分别为2.739、2.536和3.145 g·cm-3.
考虑粗骨料粒径对膏体料浆离析性能的影响[25],本文所用的废石为粒径在1 cm以下的废石,应用筛分法确定其粒径组成,0.5~1 cm的废石质量分数为98.90%,废石粒级分布如表1所示.同时,采用欧美克TopSizer激光粒度分析仪分析全尾砂和胶固粉的粒径组成,所得粒径分布如图1所示.可以看出,胶固粉的粒径非常小,都在100 μm以下;全尾砂中-20 μm和-200 μm颗粒的质量分数分别为27.14%和85.94%.

图1 全尾砂和胶固粉粒径分布Fig.1 Particle size distribution of full-tailings and glue powder
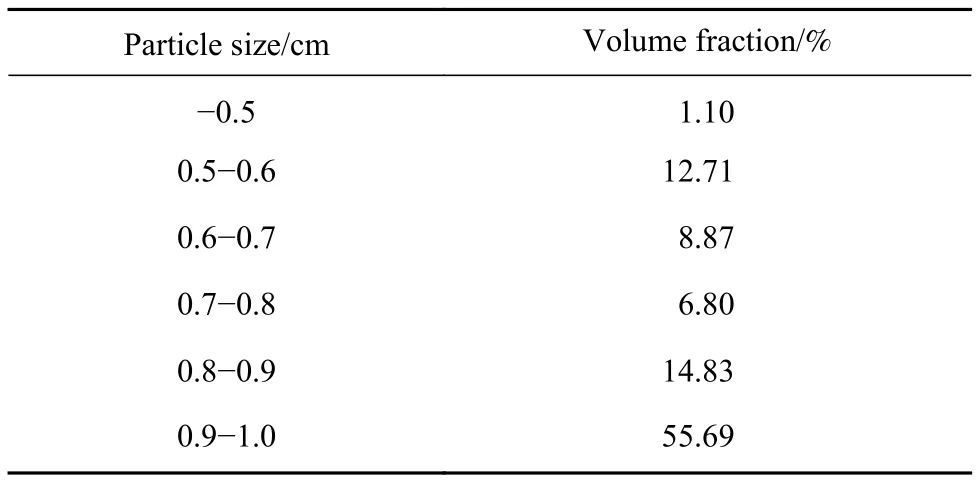
表1 废石粒级分布Table 1 Particle-size distribution of waste rock
实验过程中用实验室的自来水混合搅拌全尾砂、废石和胶固粉,按照膏体质量分数、废石掺量和胶固粉耗量制备全固废膏体.
1.2 实验方案
本文重点研究全固废膏体中固体质量分数(SF)、废石掺量(WRD)和胶固粉耗量(GPD)三个参数对全固废膏体的塌落度(S)、屈服应力(τ0)、单轴抗压强度(UCS)和泌水率(BR)的影响.
SF是指全固废膏体中所有固体(全尾砂、废石和胶固粉)的质量分数,WRD是指废石的质量与全尾砂的质量之比,GPD是指胶固粉质量与全尾砂和废石质量之和的比值.
S由标准塌落度桶测得,τ0为采用ICAR流变仪测得的全固废膏体料浆的动态屈服应力,UCS为全固废膏体在温度为20 ℃、相对湿度为90%±2%的条件下养护28 d后所测得的单轴抗压强度,BR为泌水量与全固废膏体质量的比值.ICAR流变仪属于混凝土流变仪,应用四叶桨式转子,桨叶高度为127 mm、半径为63.5 mm,测试容器半径为143 mm,适合测含有粗骨料的料浆的流变参数.ICAR流变仪的具体测试方法在相关文献已详细介绍[26].
针对全固废膏体研究的多参数多目标优化,本文采用正交实验设计分析各参数对各个目标的影响规律.基于前期探索实验,每个参数各设置四个水平,按照L16(43)正交实验表,本文实验方案设计如表2所示.

表2 L16(43)正交实验表及实验结果Table 2 Parameters and results of the L16(43) orthogonal experiment
1.3 多目标优化方法
本文中有S、τ0、UCS和BR四个响应目标,因此采用Derringer和Suich提出的总评归一值法进行多目标优化[27].在总评归一值法中,通过求解总评归一值函数(OD)的最大值,获得最优参数.
在本文OD函数中,首先基于正交实验结果,建立各个响应目标关于三个参数的二次多项式回归模型,如式(1)所示.
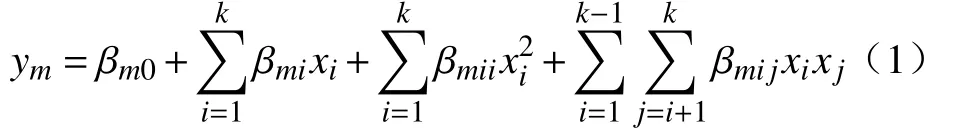
其中,ym为响应目标,本文中y1、y2、y3和y4分别为S、τ0、UCS和BR 的值;xi和xj为影响参数,本文中x1为SF、x2为废石掺量WRD、x3为GPD;k为影响参数的个数,本文中为3;βm0、βmi、βmii和βmij分别为常数项、一次项、相互作用项和平方项的回归系数.
然后采用单边变换函数对响应目标ym转换成值为0~1的期望函数dm,对于实际中期望越小越好的响应目标ym采用式(2)进行转换,而对于期望越大越好的响应目标ym采用式(3)进行转换.

其中,ym,min和ym,max分别为实验中响应目标ym的最小值和最大值,w为权重因子,通常设置为0.3[28-29].
再基于各个响应目标的期望函数dm的几何平均数,建立OD函数如式(4)所示.
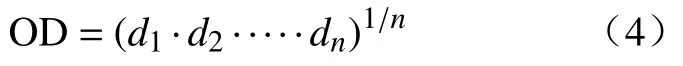
其中,OD的值为[0,1],n是响应目标的个数.
最后应用MATLAB软件求解OD的最大值确定最优参数.
2 结果分析与讨论
2.1 正交实验结果
根据正交实验方案,获得正交实验结果如表2和图2所示.
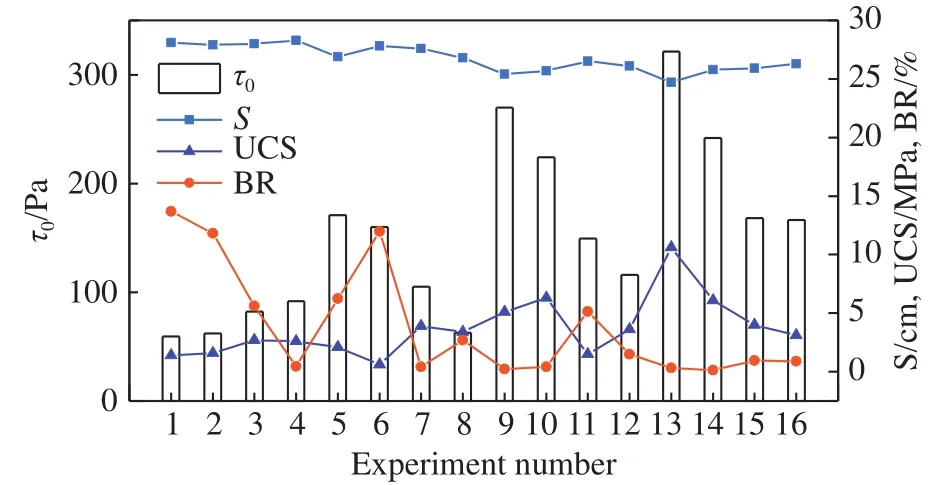
图2 正交实验结果的变化规律Fig.2 Evolution of orthogonal experiment results
不同配比条件下全固废膏体的τ0变化显著,最小值和最大值分别为59.439 Pa和321.436 Pa.全固废膏体的S值变化不明显,在25~28 cm的小范围内波动.全固废膏体的UCS变化显著,最大值达到了10.6 MPa而最小值仅为0.6 MPa.同时,第1组实验中全固废膏体的泌水现象最明显,BR达到了13.69%;而第9组实验中全固废膏体基本不泌水,BR仅为0.21%.
从图2可看出,UCS的变化趋势基本和τ0一致,但是第4、5组实验之间和第9、10组实验之间的UCS的变化趋势却和τ0相反;同时,BR的变化趋势基本和τ0、UCS相反,第4、5组实验之间的变化趋势却和τ0相同,第9、10组实验之间的变化趋势却和UCS相同.UCS和BR的变化趋势中出现“异常趋势”的原因可能是WRD和GPD交互作用的影响.
根据国家标准《全尾砂膏体充填技术规范》的规定[24],全尾砂膏体性能指标的建议范围如表3所示.对比表2和表3,可以发现全固废膏体的S均大于18 cm,同时除了第9、10、13和14组实验外τ0都小于200 Pa,说明本文中的全固废膏体具有较好的流动性与输送性能.同时,UCS均大于0.2 MPa且部分大于5 MPa,说明全固废膏体具有较好的力学性能.但是,BR均不在规定的范围内,仍需要对SF、WRD和GPD进行优化.

表3 全尾砂膏体的性能指标范围Table 3 Property range of full-tailings paste
2.2 全固废膏体性能单目标优化分析
根据正交实验方案,应用Minitab软件进行极差分析,确定各个响应目标的主要影响参数、各参数对各响应目标的最优水平以及各个响应目标的最优参数组合.极差分析结果如图3所示.

图3 基于极差分析的各响应目标随参数(a)SF,(b)WRD,(c)GPD 的变化规律Fig.3 Evolution of each response with (a) SF, (b) WRD, and (c) GPD by range analysis
2.2.1 全固废膏体的塌落度优化分析
由图3可知,全固废膏体的S随着SF的增大而先降低后升高,在SF=80%处达到最小值25.47 cm.因为SF增大过程中,WRD和GPD也在不断变化,进而导致S随SF的变化规律和全尾砂膏体随固体质量分数的变化规律[13,30]不同.添加废石后,全固废膏体内颗粒之间的摩擦力发生改变,导致S随着WRD的增大而先升高后降低,在WRD=15%处达到最大值27.05 cm.同时,虽然S随着GPD的增大先降低后增大,但是GPD>1∶8后S基本稳定在26.5 cm左右.S与GPD的非线性关系与全尾砂膏体的S随着水泥耗量的增大而不断波动的现象相似[13,30].
通过比较极差大小可知,参数SF的极差最大(2.50)、WRD 的极差最小(0.52),说明三个参数中SF对的影响S最显著,各参数对S的影响显著性顺序为:SF > GPD > WRD.对于全固废膏体,S越大,流动性越好.因此,以S最大为目标进行分析,在本文实验的范围内,各参数的最优水平分别为:SF=77%、WRD=15%、GPD=1∶10,进而得到最优参数组合为SF1GPD1WRD3.
2.2.2 全固废膏体的屈服应力优化分析
全固废膏体的τ0分别与SF和WRD呈正相关和负相关,而随着GPD的增大先降低后增大.τ0随着SF的变化规律和全尾砂膏体的τ0相似[31].随着SF的增加,全固废膏体内颗粒间的距离减小,相互作用力增强,从而导致τ0增大.同时,因为废石的粒径大于全尾砂,比表面积较小,因此保水性能较差,从而导致添加废石越多,屈服应力越低.但是,因为SF、WRD和GPD三者的共同作用,导致τ0随着GPD并不呈现出单调递增或者单调递减的关系,因为添加的废石改变了全固废膏体中固体颗粒的粒径分布,进而影响流变特性[32].
通过极差分析可知,SF对τ0的影响最显著,各参数对τ0的影响显著性顺序为:SF > WRD > GPD.对于全固废膏体,τ0越大,管道输送阻力越大,不利于全固废膏体充填的成本控制与稳定性.因此,以τ0最小为目标进行分析,各参数的最优水平分别为:SF=77%、WRD=20%、GPD=1∶8,进而得到最优参数组合为SF1WRD4GPD2.
通过坍落度和屈服应力的分析可知,坍落度和屈服应力有一定的关系.但因为坍落度不仅仅与屈服应力有关,还与全固废膏体的黏度相关,因此屈服应力越大、并不意味着坍落度越小,不能简单地建立屈服应力与坍落度之间的关系模型.
2.2.3 全固废膏体的单轴抗压强度优化分析
全固废膏体的UCS随着SF和GPD均近似呈正向线性关系,这与全尾砂膏体的UCS的变化规律相同[29-30].因为GPD的增加导致水化产物的增多从而导致UCS增大.同时,因为添加了废石后在废石表面形成界面过渡区,导致UCS随着WRD的增大先降低.但是,因为本文中多参数的共同作用,以及废石颗粒矿物性质与表面形貌的影响[33-34],导致UCS并不随着WRD呈线性关系,而是随着WRD的增大先降低,在WRD=15%处降至最小之后略有上升.
通过极差分析可知,GPD对UCS的影响最显著,各参数对UCS的影响显著性顺序为:GPD >SF >WRD.对于全固废膏体,UCS越大,充填体的稳定性越好,对于采空区的治理以及地压管理越有利.因此,以UCS最大为目标进行分析,各参数的最优水平分别为:SF=81%、WRD=5%、GPD=1∶4,进而得到最优参数组合为GPD4SF4WRD1.
2.2.4 全固废膏体的泌水率优化分析
全固废膏体的BR随着SF和GPD均近似呈负向线性关系,而随着WRD的增大先增大后降低.泌水率主要与颗粒的保水性相关:随着SF增大,全固废膏体中的自由水含量相对减少,保水性增加,从而导致泌水率降低;胶固粉的粒径小于尾砂,比表面积大,从而全固废膏体的保水性的增加随着GPD的增大而增大,进而导致泌水率降低;废石较粗,比表面积小,保水性差,同时由于多因素的作用,从而导致BR随着WRD的增大先增大后降低.
通过极差分析可知,GPD对BR的影响最显著,各参数对UCS的影响显著性顺序为:GPD >SF >WRD.对于全固废膏体,BR越大,井下泌水越少,井下环境污染越少.因此,以BR最小为目标进行分析,各参数的最优水平分别为:SF=81%、WRD=20%、GPD=1∶4,进而得到最优参数组合为GPD4SF4WRD4.
2.3 全固废膏体性能多目标优化分析
根据上述单目标优化分析可知,不同响应目标的最优参数组合各不相同,S最大时τ0并不是最小,τ0最小时UCS并不是最大,BR最小时UCS也并不是最大.同时,根据国家标准《全尾砂膏体充填技术规范》的规定[24],各个响应目标并非是越大越好或越小越好,而是应该在一个区间范围内取一个最优值,因此需要根据标准规定确定最优参数组合.但是,从表2中可看出BR均不在规定的范围内,不能寻找出符合规定的最优参数组合.为此,本文采用总评归一值法进行多目标优化.
根据表2中的正交实验结果和式(1),可得各响应目标的回归模型如式(5)~(8)所示.

根据表3中的全尾砂膏体的性能指标范围,S在18~26 cm的范围内越大越好,τ0在100~200 Pa的范围内越小越好,UCS在0.2~5 MPa的范围内越大越好,BR在1.5%~5%的范围内越小越好,因此根据响应目标ym转换为期望函数dm的方法,建立各个响应目标的期望函数如式(9)~(12)所示.
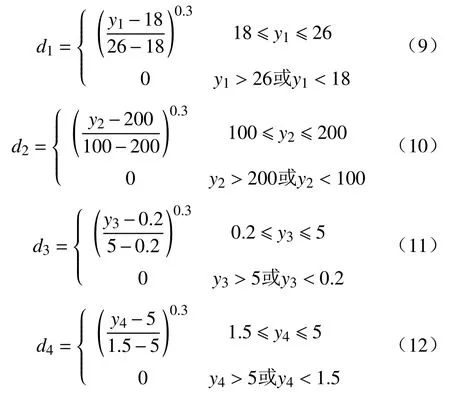
进而建立本文的OD函数如式(13)所示.
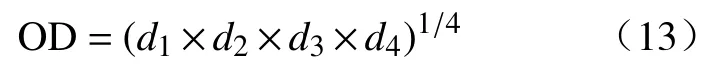
应用MATLAB软件求解OD的最大值,得到本文的最优参数为:SF=79.31%、WRD=18.86%、GPD=3∶20.在最优参数条件下,OD=0.9678,对应的S=25.45 cm、τ0=100.49 Pa、UCS=3.55 MPa、BR=1.50%.
为了验证所确定最优参数的准确性,在最优参数条件下进行验证实验,所得结果为S=25.8 cm、τ0=106.137 Pa、UCS=3.3 MPa、BR=1.64%.因此,模拟优化结果和实际结果相比,误差均在±10%以内,说明多目标优化所得结果是可信的.
需要说明的是,在本文中式(5)~(8)的各项系数以及多目标优化所得结果的精度均为两位小数,在应用MATLAB进行实际求解时为了减小计算过程取近似值产生的计算误差,设置的精度为14位小数.
3 结论与展望
本文在全尾砂膏体充填的基础上提出了全固废膏体充填,分析了固体质量分数、废石掺量和胶固粉耗量对全固废膏体的塌落度、屈服应力、单轴抗压强度和泌水率的影响,在结合国家标准规定的范围应用总评归一值模型进行全固废膏体关键性能指标的多目标优化,主要结论如下:
(1)全固废膏体的关键性能指标和全尾砂膏体相似,一定条件下具有良好的流动性与输送性能,同时全固废膏体的力学性能也可在较大范围内调整以适应不同的充填要求,并且泌水性随物料配比的变化较大.
(2)对全固废膏体的S、τ0、UCS和BR 四个响应目标,影响最显著的参数和最优参数组合各不相同,无法通过单目标优化确定满足各个响应目标均最优的参数组合.
(3)本文提出的应用总评归一值模型可以进行全固废膏体关键性能指标的多参数多目标优化,可为实际应用及其他矿山膏体的多目标优化提供参考.
本文初步对全固废膏体的关键性能指标进行了优化,由于全固废膏体的充填材料涉及多种固废、固废颗粒尺寸涉及多个数量级、性能涉及多个指标要求,因此未来还需考虑废石的种类与形貌、固废颗粒的粒级组成等更多参数对全固废膏体的线缩率、凝结时间等更多的性能指标的影响.
