深部地下硐室与应力场轴变关系及其围岩损伤破裂分析
2022-04-07刘力源纪洪广
刘力源,张 乐,纪洪广✉
1) 北京科技大学土木与资源工程学院,北京 100083 2) 北京科技大学城市地下空间工程北京市重点实验室,北京 100083
随着我国经济与社会的不断发展,浅部资源日益枯竭,矿产资源和地下空间开发利用的需求日益增长[1-3].理论上,地球内部从地表到地层以下10000 m处均为成矿空间.因此,为满足人类社会发展的需要,深部地层矿产资源开采是解决资源短缺问题的有效途径[4-5].深部开采和地下空间工程成为未来发展的必然趋势.
随着地层深度增加,地层应力、地温和孔隙水压显著提高,深部围岩处于“三高一扰动”的复杂地质力学环境,其力学行为与变形机制不同于浅部地层[6-7],在深部开采中,会有岩爆、片帮等特殊的破坏现象出现[8-10].国内外很多学者针对深部地下硐室开挖和支护进行了理论分析、数值模拟及原位试验等工作,取得了一系列成果[11-15].值得特别关注的是,深部地下硐室的形状、大小及其布置对围岩损伤破裂和稳定性具有重要的影响.在“三高一扰动”的环境中,高地应力是引起地下硐室围岩变形、损伤和破坏的根本作用力.岩体中地应力绝大多数是以水平应力为主的三向不等压的空间应力场.于学馥和乔端[16],以及于学馥[17]提出地下硐室轴比变化对围岩变形和破坏起重要控制作用的理论,称轴变论.
在实际工程中,深部硐室开挖形成的围岩损伤区域(EDZ),损伤区域的产生显著影响深部地下硐室的围岩稳定性,该区域的岩石渗透率通常要比原岩高得多[18],因此对硐室开挖损伤区域的评估是设计深部硐室的一项关键任务.Falls和Young[19]通过声发射与超声波手段,指出处于高应力条件下岩体,应力重分布与扰动造成的损伤要严重于低应力条件下.Hakami[20]、Read等[21]通过弹性分析与弹塑性分析的数值方法对损伤区域进行评估.Chang等[22]研究了一种基于室内试验的损伤模型并使用Fish将其应用于开挖损伤区的模拟.张小波等[23]对巷道围岩力学状态进行极限平衡分析,推导出围岩损伤破裂半径及应力场分布的解析表达式.蔡德所等[24]基于三峡工程基岩开挖爆破建立了基岩爆破的损伤本构模型,将其嵌入SHALE程序中,实现了对基岩开挖爆破损伤范围的数值模拟.杨栋等[25]通过岩体声波测试,确定梅花山隧道的围岩损伤范围,并采用FLAC软件模拟表明地应力大小对围岩损伤分布有着显著影响.
本文针对深部地下硐室轴比、地应力与围岩稳定性关系,开展了硐室断面形状、侧压系数和构造应力场对围岩损伤破裂的影响.随着地层深度增大,硐室围岩损伤破裂程度加剧,提出了临界侧压系数概念用以指导深部地层硐室设计及稳定性分析.以三山岛金矿西岭矿区拟建的井深为2005 m的副井为工程依托,开展硐室断面设计与损伤破裂关系数值模拟,以期助力深部地层巷道科学合理布置.
1 深部地下硐室轴比和地应力关系
地下工程中常采用椭圆形硐室断面,图1给出了不同角度(β)地应力作用下硐室开挖硐壁应力计算简图.根据弹性力学的解,将两个主应力作用下求得的应力叠加,椭圆形硐室硐壁的应力为:
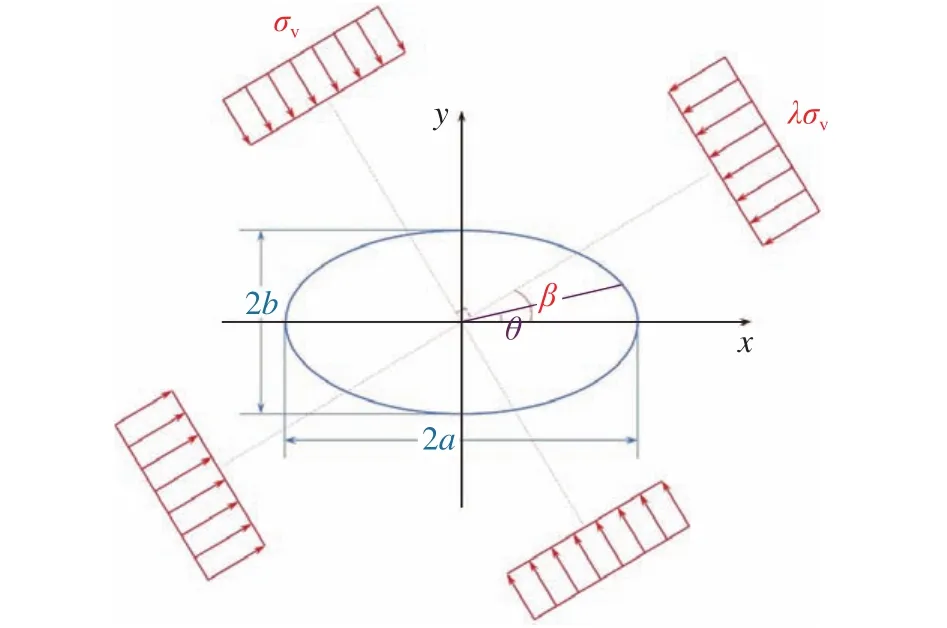
图1 不同地应力场作用下椭圆形硐室应力计算简图Fig.1 Stress calculation diagram of an oval chamber under various in situ stress fields
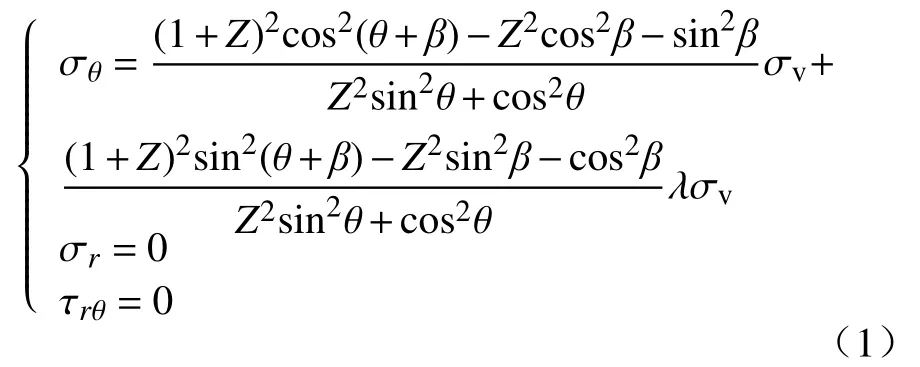
其中,σθ为极坐标下围岩切向应力;σr为极坐标下围岩径向应力;τrθ为极坐标下围岩剪应力;Z为x轴正半轴a与y轴上半轴b的比值,Z=a/b;θ为硐壁上任意一点到椭圆形硐室中心点连线与x轴的夹角;β为侧向主应力作用线与x轴的夹角,β≠0时,椭圆形硐室为构造应力状态;λ为地应力侧压系数;σv为竖向主应力,β=0时,σv为上覆岩层自重应力.
针对β=0时,椭圆形硐室竖向轴端点(θ=π/2和3π/2)切向应力σθt和水平轴端点(θ=0和π)切向应力σθ1的变化相对应,其中一对为最大值,另一对为最小值.
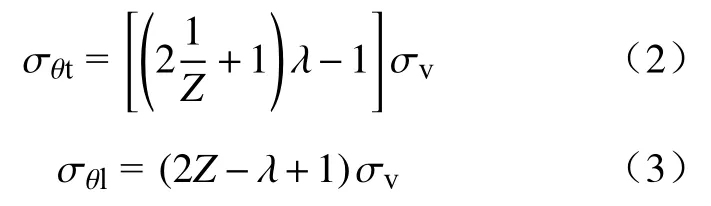
需要特别指出的是,存在围岩应力均匀分布的硐室轴比,于学馥先生称之为“等应力轴比”,也称“谐硐”.等应力轴比具有以下特点,围岩应力均匀分布,不出现拉应力,出现的最大应力值最小,即由于开挖引起的应力集中最小.等应力轴比与地应力测压系数λ的关系,经计算求得Z=λ.
将β=0和Z=λ代入式(1),即得:
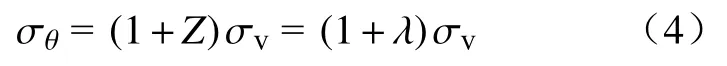
由式(4)可知,等应力轴比条件下硐壁的切向应力与θ无关,并且在λ≠1的条件下为均匀压应力,且其应力值小于圆形硐室λ=1时硐壁切向应力值.因此,等应力轴比规律确定的椭圆形硐室断面是最稳定的几何形状.图2给出了不同侧压系数下等应力轴比硐室围岩应力分布情况.
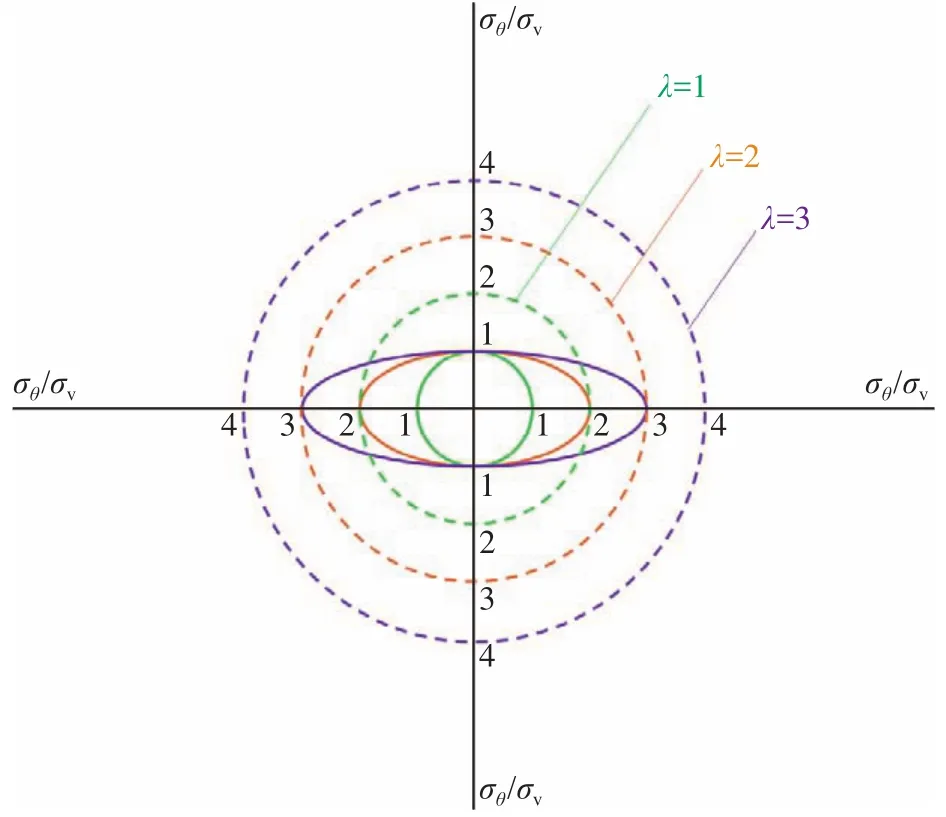
图2 等应力轴比硐室应力集中系数变化Fig.2 Stress concentration factor for a chamber where the axial ratio equals the stress ratio
2 围岩损伤破裂数值模拟
采用弹性损伤力学理论对不同工况下的深部地下硐室围岩损伤破裂进行数值模拟,以探究硐室应力场轴变与围岩损伤破裂的对应关系.硐室埋深2000 m,竖向主应力为50 MPa,侧压系数λ为1.5,即水平主应力为75 MPa.地层所处的花岗岩单轴抗压强度为132.3 MPa,拉伸强度为12.4 MPa,弹性模量为42.7 GPa.借助于Weibull分布函数生成深部地层非均质岩体力学参数,围岩非均质系数取8,如图3所示,硐室开挖数值模型边长为30 m,开挖断面面积为20 m2,模型上边界为竖向应力σv,模型右边界为最小水平主应力σh,模型的下边界和左边界为滚动约束.采用最大拉应力准则和Mohr-Coulomb准则进行损伤判别,并基于COMSOL Multiphysics with MATLAB平台进行硐室围岩损伤破裂数值模拟分析[26-29].
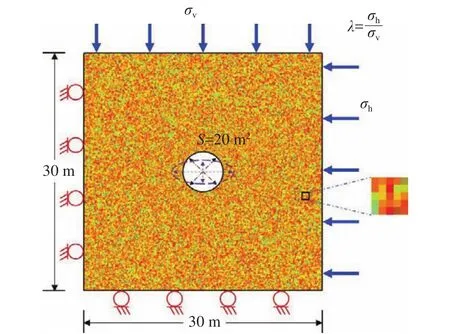
图3 硐室开挖数值模型Fig.3 Numerical model for chamber excavation
2.1 硐室断面轴比对围岩损伤破裂影响
轴变论指出地应力条件不变时,椭圆形硐室的长短轴之比是影响巷道稳定性的重要因素,并提出了“等应力轴比”、“零应力轴比”、“压应力轴比”与“拉应力轴比”的不同硐室形状.由第1节分析可知,等应力轴比的围岩应力均匀分布,不出现拉应力且最大应力值为最小,等应力轴比条件下巷道的围岩是最稳定的.
为探究不同轴比对围岩损伤破裂影响情况,构建侧压系数λ=1.5的地应力条件下不同轴比硐室,分别设定Z=1/3、1/2、2/3、1时的拉应力轴比,Z=1.5时的等应力轴比及Z=2、3时的压应力轴比;且硐室断面面积均为20 m2.各轴比条件下损伤破裂区及弹性模量演化如图4和图5所示,硐室顶部和中线两帮应力分布如图6所示.
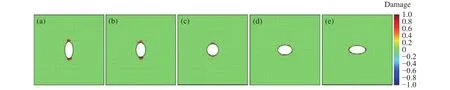
图4 硐室断面轴比对围岩损伤破裂影响.(a)Z=1/2;(b)Z=2/3;(c)Z=1;(d)Z=3/2;(e)Z=2Fig.4 Effect of the chamber axial ratio on the damage of country rock: (a) Z=1/2; (b) Z=2/3; (c) Z=1; (d) Z=3/2; (e) Z=2
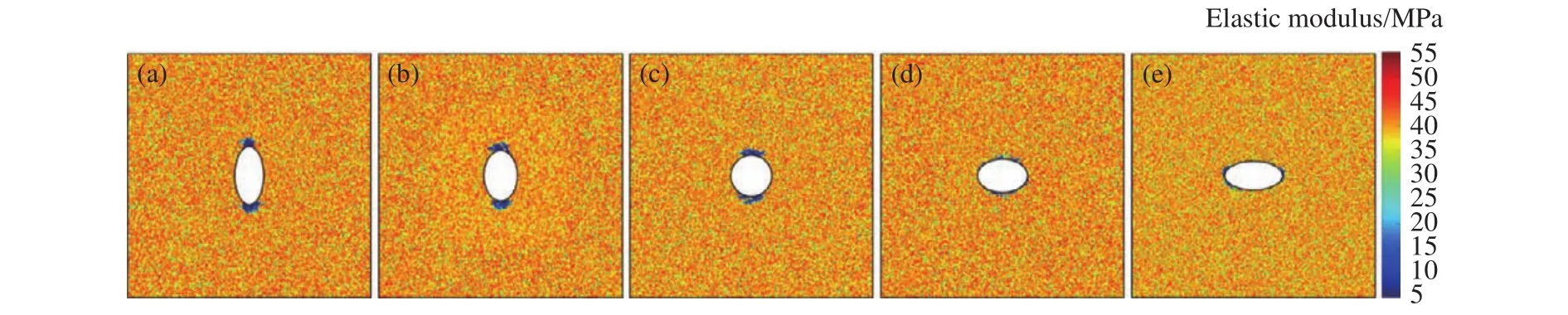
图5 硐室断面轴比对围岩弹性模量的影响.(a)Z=1/2;(b)Z=2/3;(c)Z=1;(d)Z=3/2;(e)Z=2Fig.5 Effect of the chamber axial ratio on the elastic modulus of country rock: (a) Z=1/2; (b) Z= 2/3; (c) Z=1; (d) Z=3/2; (e) Z=2
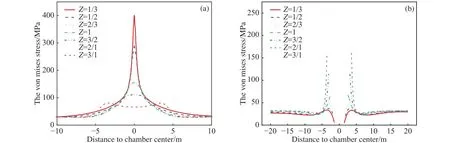
图6 不同轴比硐室X方向应力分布情况.(a)拱顶处;(b)水平中线处Fig.6 Stress distribution in the X direction of the chamber with various axial ratios: (a) chamber roof; (b) middle route of the chamber
数值模拟结果表明,侧压系数λ= 1.5的地应力条件下,拉应力轴比硐室的应力集中区域主要表现在拱顶与拱底位置,损伤破裂区亦分布在拱顶和拱底.压应力轴比围岩的应力集中情况与损伤区域均与拉应力轴比相反.等应力轴比时,应力围绕硐室均匀分布,且最大应力为130 MPa,均小于其余轴比硐室最大应力值,等应力轴比条件下,损伤区呈围绕硐室零星分布.
不同的轴比条件下,硐室围岩损伤破裂区大小不同.如图7所示,等应力轴比条件下,围岩损伤区域面积最小,为2.21 m2;压应力轴比损伤面积次之;拉应力轴比相对损伤面积最大.因此,在实际工程中硐室断面设计应避免拉应力轴比情况.此外,地应力条件不变的情况下,硐室轴比与等应力轴比差别越大,损伤破裂区面积越大.
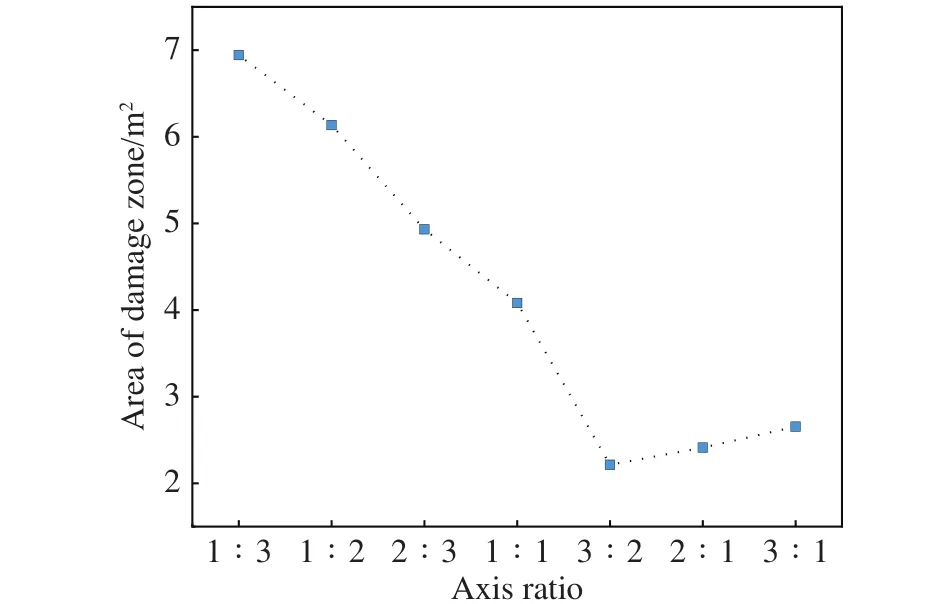
图7 围岩损伤破裂区与硐室轴比条件关系Fig.7 Relationship between the damaged zone and chamber axial ratio
2.2 硐室断面形状对围岩损伤破裂影响
根据地下工程的实际用途,往往会采用不同形状的硐室断面设计.不同的硐室断面形状对应于不同程度的应力集中,对硐室围岩损伤破裂具有重要影响.本节构建硐室面积为20 m2的圆形、椭圆形(轴比Z=1.5)、马蹄形、矩形(长短轴比为1.5)和正方形硐室进行围岩损伤破裂过程的数值模拟.图8和图9分别给出了椭圆形、矩形、圆形、马蹄形和正方形硐室围岩损伤破裂区和弹性模量分布云图.
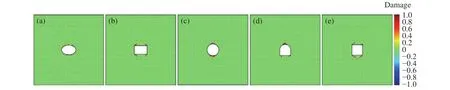
图8 硐室断面形状对围岩损伤破裂影响.(a)椭圆形;(b)矩形;(c)圆形;(d)马蹄形;(e)正方形Fig.8 Effect of the chamber shape on the extent of damage of country rock: (a) ellipse; (b) rectangle; (c) circle; (d) horseshoe; (e) square
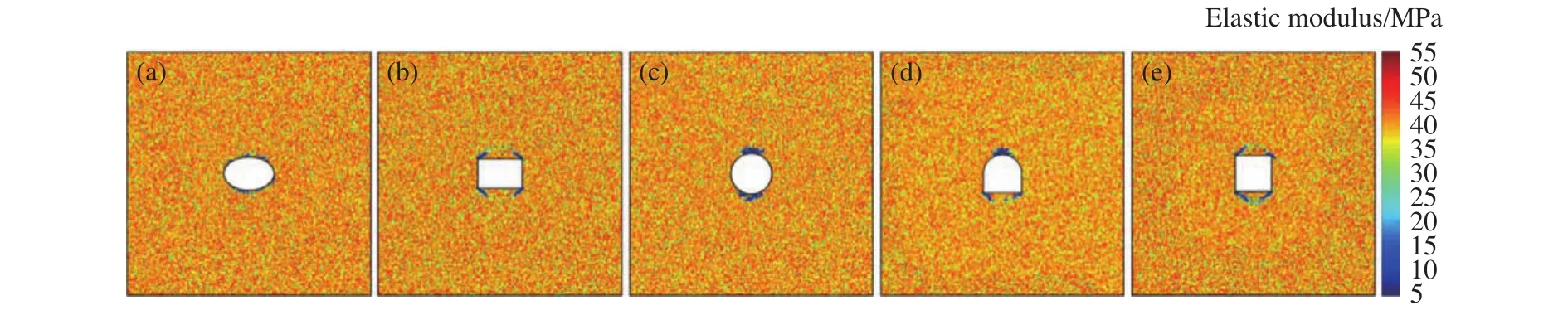
图9 硐室断面形状对围岩弹性模量影响.(a)椭圆形;(b)矩形;(c)圆形;(d)马蹄形;(e)正方形Fig.9 Effect of the chamber shape on the elastic modulus of country rock: (a) ellipse; (b) rectangle; (c) circle; (d) horseshoe; (e) square
如图10所示,相较于圆形、椭圆形硐室,其余形状硐室在直角处均产生较大程度应力集中,应力最大值高达531 MPa,诱使该区域围岩发生损伤破裂现象.矩形、正方形硐室围岩损伤破裂演化过程表明,损伤破裂区轮廓向近似于椭圆形发展,证实了于学馥先生提出的椭圆形硐室是各种形状巷道破坏后的最终形态[16-17].需要指出的是,损伤力学计算结果表明,尽管在矩形、马蹄形和正方形硐室边角处产生了较大应力集中,其损伤破裂区范围不会大幅增大或无限扩展.围岩的损伤破裂将会大幅降低边角处应力集中区域的应力集中程度,并调整该区域力学平衡.
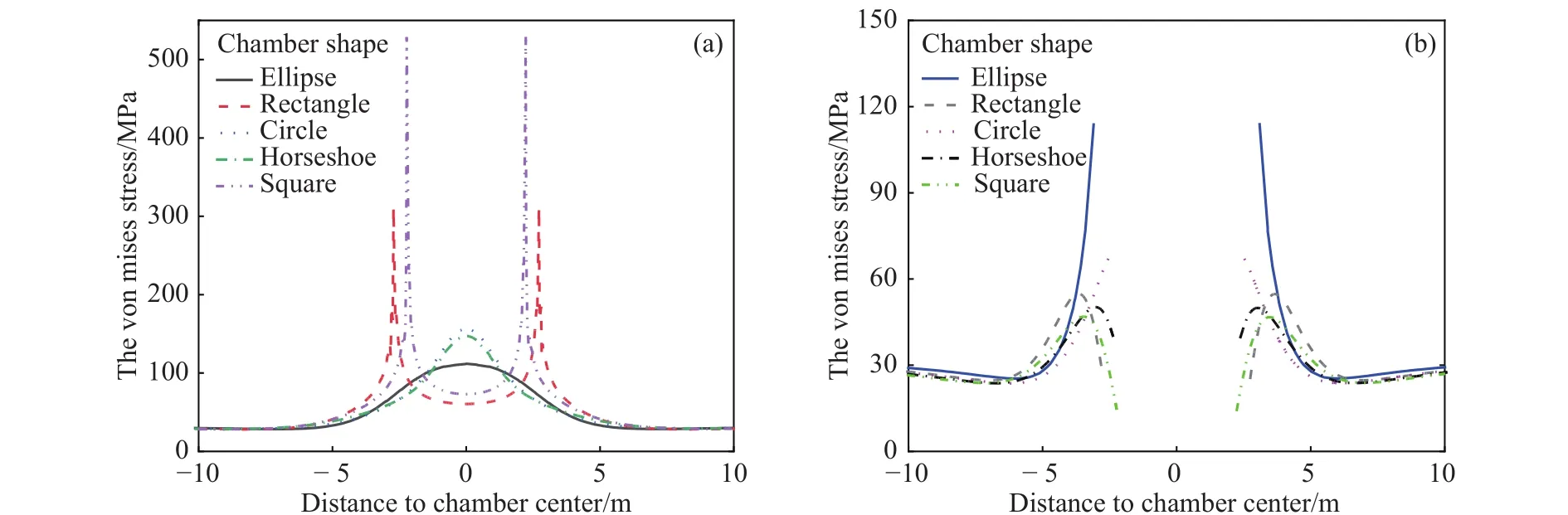
图10 不同形状硐室X方向应力分布情况.(a)拱顶处;(b)水平中线处Fig.10 Stress distribution in the X direction of a chamber with various shapes: (a) chamber roof; (b) middle route of the chamber
统计各断面形状硐室围岩损伤破裂区面积可知,等应力轴比椭圆形硐室围岩损伤破裂区面积最小2.21 m2,其次为与侧压系数相等轴比的矩形硐室3.52 m2,正方形硐室损伤破裂区面积最大5.58 m2,如图11所示.尽管矩形硐室和正方形硐室断面面积相同,然而矩形硐室损伤破裂区面积远小于正方形硐室.由此可见,相同地应力条件下,硐室断面设计应先以地应力条件为主要参考,依据硐室使用功能设计最符合地应力条件的硐室断面,从而有效控制围岩损伤破裂区范围.
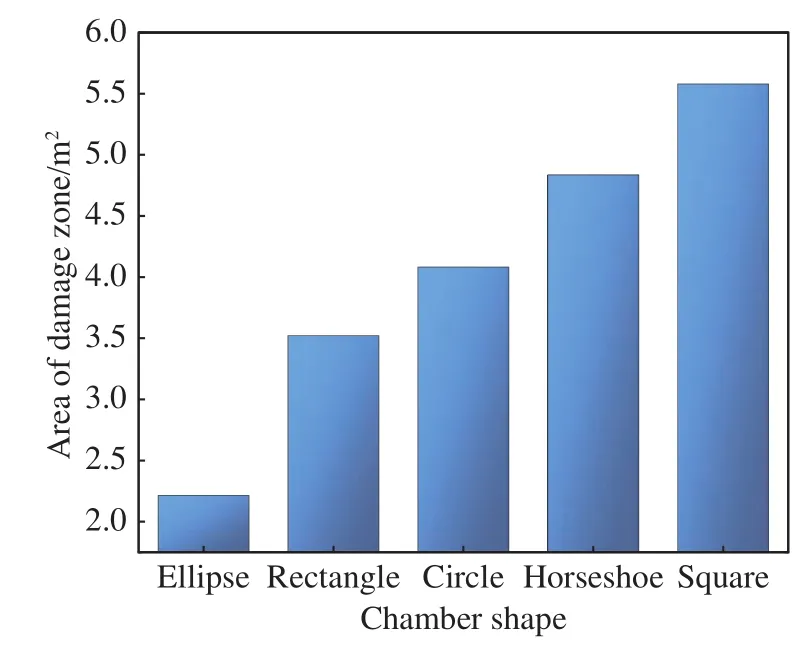
图11 围岩损伤破裂区与硐室形状条件关系Fig.11 Relationship between the damaged zone and chamber shape
2.3 地应力场对围岩损伤破裂影响
地应力是引起地下硐室围岩变形破坏的根本原因[30],是岩体力学中的重要组成部分.深部地应力分布规律多表现为水平主应力较大,竖向主应力为最小主应力;水平主应力与竖向主应力的比值即侧压系数,一般情况下为0.5~5.5,多数情况大于1.地质构造对地应力场具有重要影响,地应力量值和方向都有较大的变化;同样地,由于地下硐室群开挖或采矿等活动,区域应力场往往也会发生较大变化.
2.3.1 侧压系数对围岩损伤破裂影响
随着地层深度的增加,硐室周围原岩应力水平不断增大,尤其是在地质构造强烈地区,水平主应力远大于竖向主应力.侧压系数的增大,加剧了深部硐室开挖后围岩损伤破裂程度,也使得开挖后的支护变得更为复杂[31-32].为探究侧压系数对深部硐室变形与破坏影响,模拟了竖向主应力为50 MPa,侧压系数分别为1、1.5、1.75、2和2.2,椭圆形硐室围岩损伤破裂情况.数值模拟结果表明,低侧压系数条件下,硐室周边应力表现为压应力;侧压系数大于硐室轴比后,硐室的拱顶拱底部位出现较高的压应力集中区,损伤情况变化加剧.侧压系数越大,应力越集中于顶、底板两侧,应力集中区域多以拉伸损伤为主.图12和13给出了各侧压系数下椭圆形硐室损伤破裂区及弹性模量分布情况.如图14(a)所示,椭圆形硐室顶部Mises应力分布随侧压系数增大而不断增大.图14(b)表明,椭圆形硐室中线处Mises应力分布随侧压系数增大而不断减小.图15围岩损伤破裂区面积统计结果表明,保持椭圆形硐室断面轴比不变,围岩损伤破裂区面积随着侧压系数增大不断增大,损伤破裂区面积与侧压系数呈指数关系增长;侧压系数大于硐室轴比后,损伤破裂面积快速增大.需要特别关注的是,当侧压系数增大到一定数值时,硐室围岩将会发生非稳定破裂;将此时的侧压系数定义为临界侧压系数.图16给出了随着竖向应力增大,临界侧压系数变化规律.随着埋深的增大,硐室的轴比越趋近于1.
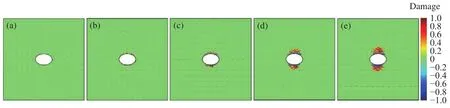
图12 侧压系数对围岩损伤破裂影响.(a)λ=1;(b)λ=1.5;(c)λ=1.75;(d)λ=2;(e)λ=2.2Fig.12 Effect of the lateral pressure coefficient on the damage of country rock: (a) λ=1; (b) λ=1.5; (c) λ=1.75; (d) λ=2; (e) λ=2.2
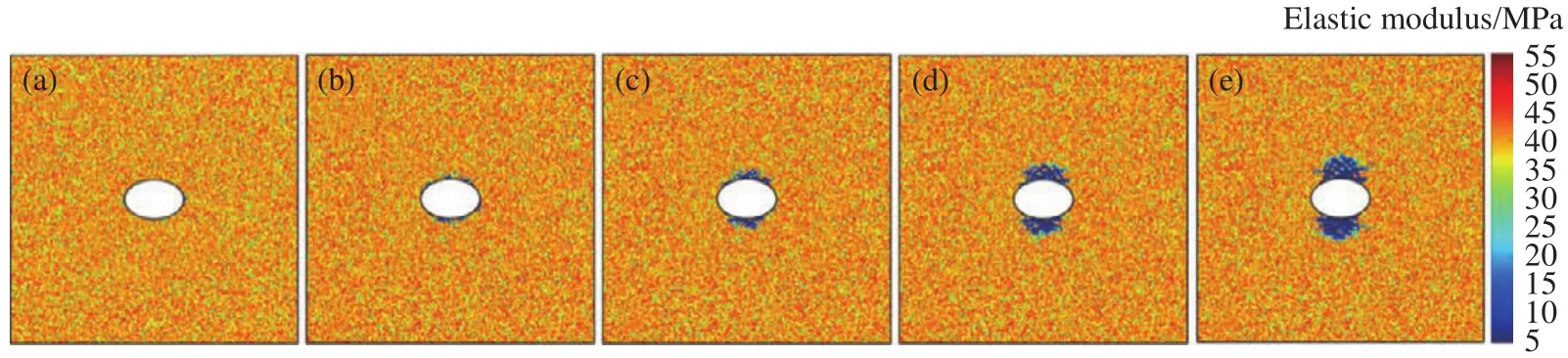
图13 侧压系数对围岩弹性模量影响.(a)λ=1;(b)λ=1.5;(c)λ=1.75;(d)λ=2;(e)λ=2.2Fig.13 Effect of the lateral pressure coefficient on the elastic modulus of country rock: (a) λ=1; (b) λ=1.5;(c) λ=1.75; (d) λ=2; (e) λ=2.2
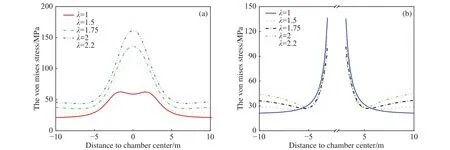
图14 不同侧压系数硐室X方向应力分布情况.(a)拱顶处;(b)水平中线处Fig.14 Stress distribution in the X direction of a chamber with various lateral pressure coefficients: (a) chamber roof; (b) middle route of the chamber
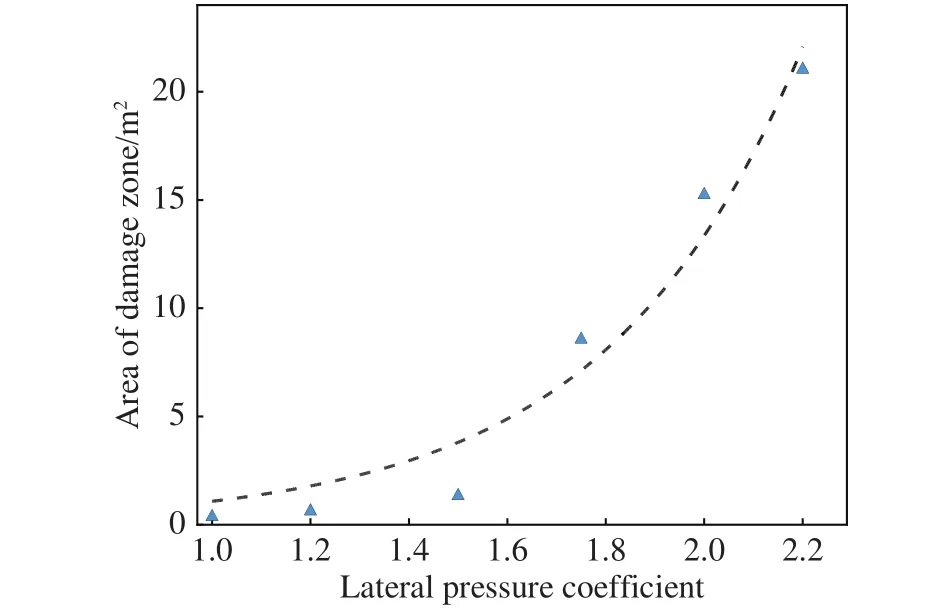
图15 围岩损伤破裂区面积与地应力侧压系数条件关系Fig.15 Relationship between the damaged zone and in situ stress lateral pressure coefficient
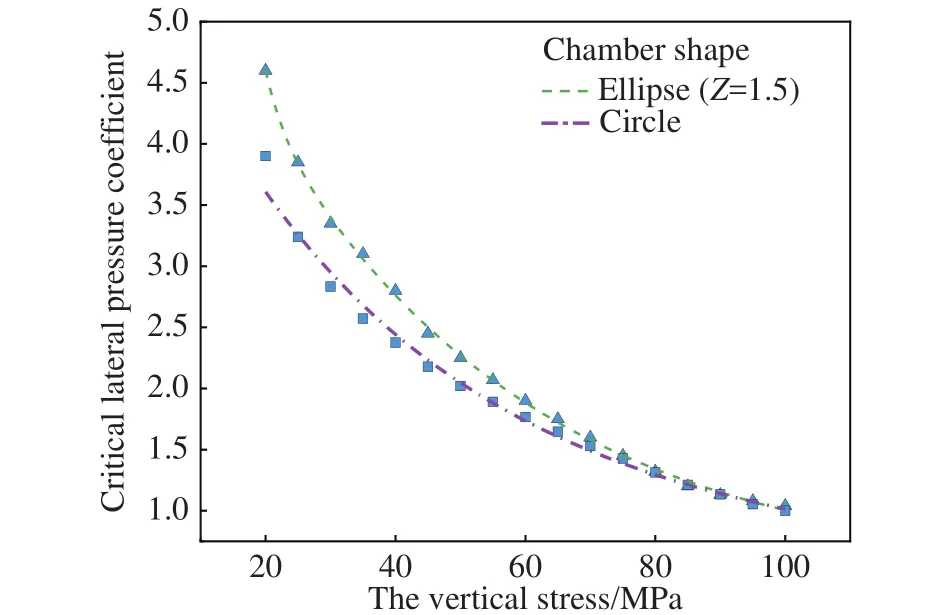
图16 不同地应力条件下对应的临界侧压系数Fig.16 Critical lateral pressure coefficient under various in situ stress conditions
保持地层条件不变,分析不同竖向应力作用下临界侧压系数变化规律.数值模拟结果表明,随着埋深增大,硐室临界侧压系数不断减小.因此,对于深部地层条件而言,侧压系数的变化对硐室围岩损伤破裂影响显著,侧压系数的微小改变可能造成硐室围岩大范围损伤破裂.
2.3.2 构造应力场对围岩损伤破裂影响
构造应力由地壳运动及各板块间的拉伸挤压构成[33].在实际工程中,一些硐室和巷道受构造应力的影响,可能会发生大变形、坍塌甚至破坏的风险,影响工程的安全高效运行.因此,构造应力场作用下硐室的布置与支护设计应与一般情况不同[34-35].
本节对侧压系数和硐室轴比不变条件下,不同β(β= 0°, 15°, 30°, 45°)构造应力场作用下硐室围岩损伤破裂过程进行了数值模拟.当β= 0°时,硐室围岩应力均匀分布且相等;β增大后,硐室围岩垂直于最大主应力处应力增大,产生明显的应力集中现象.数值模拟结果表明,硐室围岩损伤破裂区面积随着β增大呈增大趋势;β= 45°时,损伤破裂区面积最大.如图17和18所示,构造应力的方向对硐室围岩损伤破坏区位置具有重要影响.随着β增大,损伤破裂区由围绕硐室均匀分布,逐渐向垂直于最大主应力方向的应力集中处转移.图19(a)和(b)分别给出了椭圆形硐室顶部和中线处Mises应力分布,构造应力场对Mises应力分布具有重要影响.因此,深部地下硐室设计时应根据实际地应力场进行动态调整,从而有效降低构造应力对硐室围岩稳定性的不利影响,减小围岩损伤破裂区范围.图20给出了围岩损伤破裂区面积与构造应力角度间的关系.
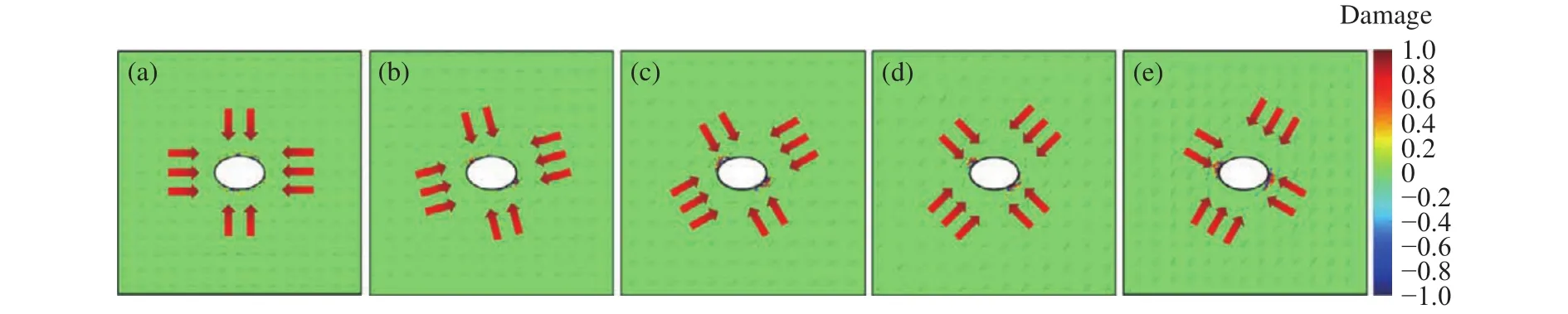
图17 构造应力角对围岩损伤破裂影响.(a)β=0°;(b)β=15°;(c)β=30°;(d)β=45°;(e)β=60°Fig.17 Effect of the tectonic stress dip on the damage of country rock: (a) β=0°; (b) β=15°; (c) β=30°; (d) β=45°; (e) β=60°
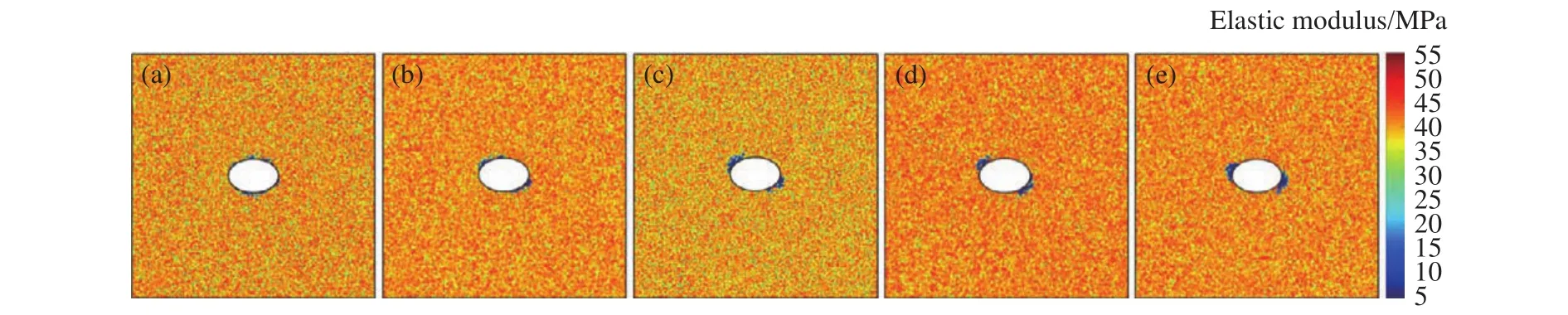
图18 构造应力角对围岩弹性模量影响.(a)β=0°;(b)β=15°;(c)β=30°;(d)β=45°;(e)β=60°Fig.18 Effect of the tectonic stress dip on the elastic modulus of country rock: (a) β=0°;(b) β=15°;(c) β=30°;(d) β=45°;(e) β=60°
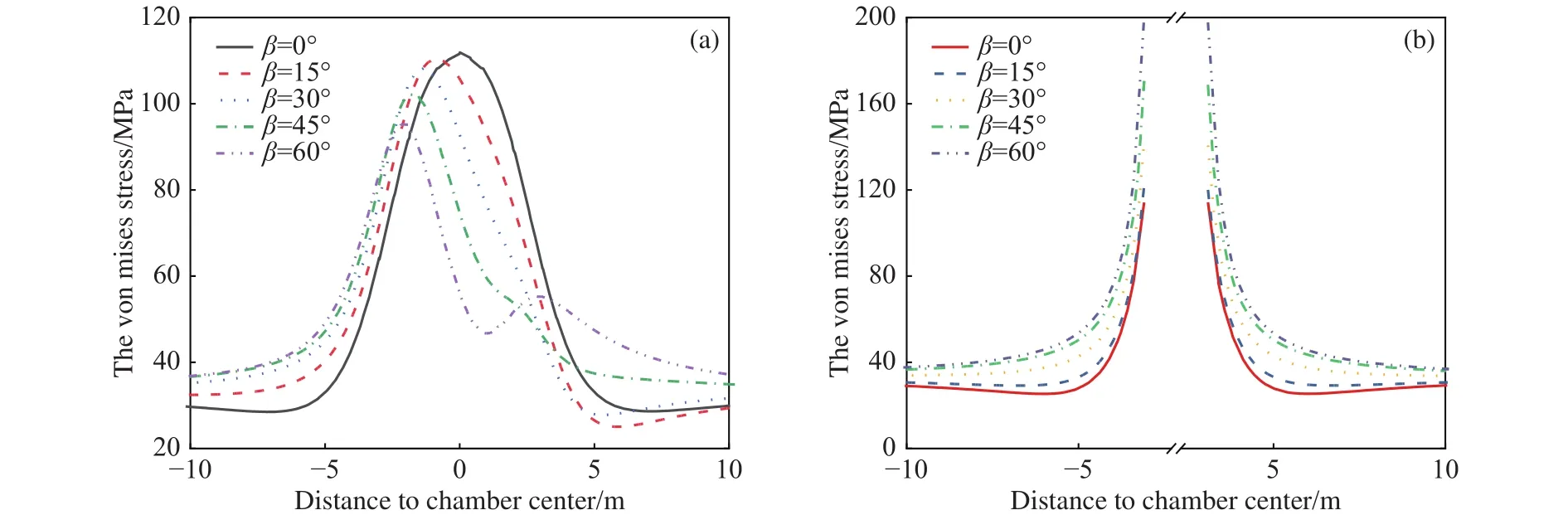
图19 不同构造应力角硐室X方向应力分布情况.(a)拱顶处;(b)水平中线处Fig.19 Stress distribution in the X direction of a chamber with different tectonic stress dips: (a) chamber roof; (b) middle route of the chamber
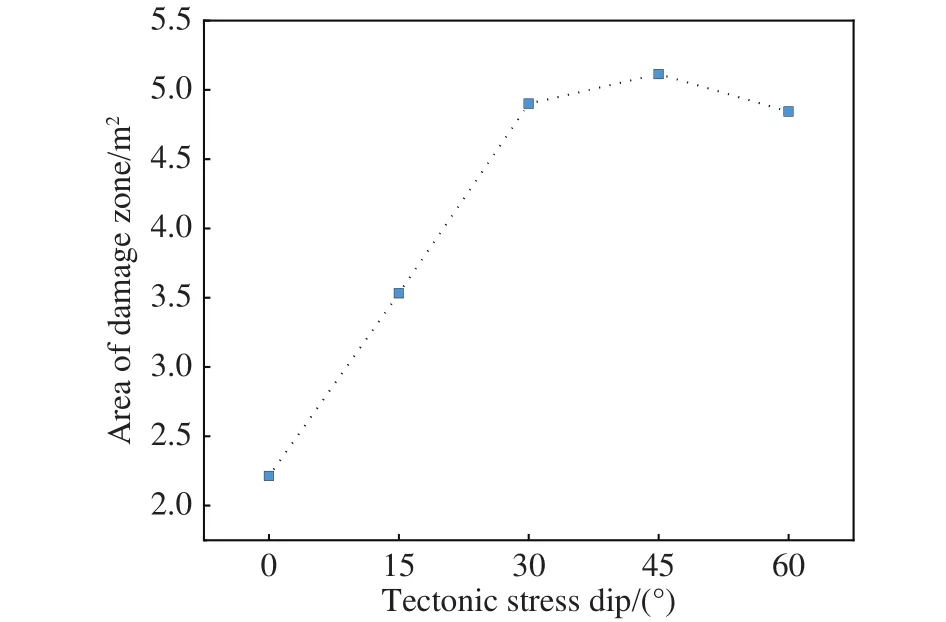
图20 围岩损伤破裂区面积与构造应力角度关系Fig.20 Relationship between the damaged zone area and tectonic stress dip
3 地下硐室断面设计与地压调控讨论
地压是引起围岩变形破坏的根本作用力,因此工程所在处的实测地应力是力学分析的前提条件.不同的地应力场,硐室断面设计及其力学分析和支护设计不尽相同.根据实测地应力,进行硐室断面设计,降低硐室围岩应力集中系数,从而科学论证硐室垮落和自稳演变过程.不同的地压具有不同的变形破坏特征和规律,应采用不同的力学理论进行机理分析,确定合理的围岩稳定性控制策略.
三山岛金矿西岭矿区规划设计了国内拟建的最深竖井,井深为2005 m.三山岛金矿西岭矿区深部地层地应力测试结果表明,埋深1900 m处地层最大水平主应力为72 MPa,最小水平主应力为48 MPa,竖向应力为50 MPa.根据轴变论的思想,巷道走向应沿最大水平主应力方向布置,而后根据最小水平主应力与竖向应力比值得到椭圆形硐室设计轴比Z= 0.96.然而,实际工程中金属矿巷道一般采用拱形巷道,本文建立了宽4 m,高4 m的三心拱巷道,并对其进行了损伤破裂分析.如图21~23所示,等应力轴比硐室应力均匀分布在巷道周边围岩,且损伤区域也围绕巷道周边零星分布,根据数值模拟结果对损伤单元进行统计可得出损伤区域面积为4.36 m2;三心拱巷道则在拱脚处产生较强的应力集中,损伤区域集中在拱脚与拱顶处,损伤区域面积为5.58 m2,略大于圆形巷道.相同巷道断面面积条件下,三心拱巷道可利用有效面积及实用性均优于圆形硐室.通过对三心拱巷道拱顶和拱脚进行适当锚喷支护可保障巷道安全服役.
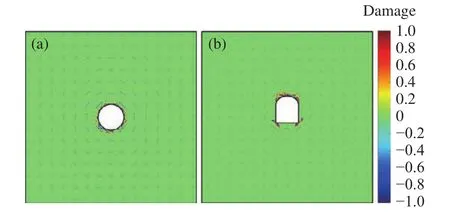
图21 三山岛金矿设计巷道围岩损伤破裂.(a)圆形;(b)三心拱形Fig.21 Damage to a roadway in the Sanshandao gold mine: (a) circle;(b) three-centered arch
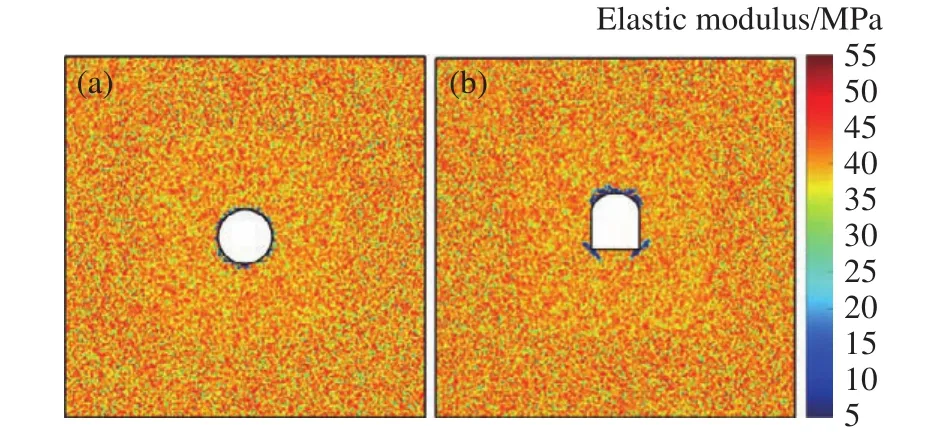
图22 三山岛金矿设计巷道围岩弹性模量.(a)圆形;(b)三心拱形Fig.22 Elastic modulus of the roadway in the Sanshandao gold mine:(a) circle; (b) three-centered arch
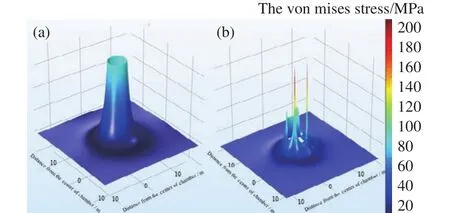
图23 三山岛金矿设计巷道 Mises应力分布情况.(a)圆形;(b)三心拱形Fig.23 The von mises stress distribution in a roadway in the Sanshandao gold mine: (a) circle; (b) three-centered arch
4 结论
(1)地下硐室开挖围岩损伤破裂程度与地层地应力和硐室断面息息相关.硐室形状与轴比是影响围岩损伤破裂的重要因素,相同开挖面积下等应力轴比的椭圆形硐室应力分布均匀,应力集中效应最小,损伤破裂区零星分布在硐室周围,损伤破裂区面积小,是硐室设计的最优解.
(2)地应力场是造成地下硐室围岩变形破坏的根本原因,侧压系数越大,硐室顶、底板处应力峰值越大,损伤破裂越严重,应力集中区围岩以拉伸破裂为主.侧压系数大于硐室轴比后,围岩损伤区域面积随侧压系数增大呈指数性增大.数值模拟结果表明,随着地层深度增大,圆形和椭圆形硐室的临界侧压系数逐渐减小并趋于1,即硐室开挖轴比的微小变化将会引起围岩严重损伤破裂.
(3)构造应力场作用下地下硐室围岩损伤破裂程度和区域发生显著变化.构造应力场角度越大,围岩损伤破坏程度越严重,损伤破裂区由均匀随机分布逐渐向垂直于最大主应力方向的围岩应力集中处转移.构造应力场作用下地下硐室开挖诱发冒顶和岩爆的风险大幅升高.
(4)实际工程中,地下硐室的设计与布置应结合实测原位地应力条件,确保硐室形状和走向符合地应力条件.硐室轴向设计应沿最大水平主应力方向,从而有效减小硐室围岩应力集中程度,最大程度降低地应力场对围岩损伤破裂及稳定性的不利影响.
致谢
谨以此文缅怀我国著名岩石力学与采矿工程专家于学馥先生.
