基于AFSA算法的两步法初值问题优化算法
2022-04-07张宇轩王宏力何贻洋肖永强张鹏飞
张宇轩, 王宏力, 何贻洋, 冯 磊, 肖永强, 张鹏飞
(1.火箭军工程大学导弹工程学院,西安 710000; 2.火箭军指挥学院作战实验室,武汉 430000)
0 引言
星敏感器是在恒星参照系下以星空为观察对象的高精度姿态敏感器,因其高达角秒级的定姿精度而在卫星等飞行器的姿态控制中被广泛使用[1]。其中,光学误差会对星敏感器的定姿精度造成严重影响,因此为保证星敏感器的定姿精度以及维护其工作的可靠性,必须要进行星敏感器的光学误差标定[2]。
星敏感器光学误差参数的标定主要是针对焦距、主点和光学畸变等参数来进行标定,而两步法因具有在估计主点和焦距的同时也标定了光学畸变且标定过程简易快速的特点,成为了最常用的标定方法[3]。但由于迭代初值的选择对标定结果的影响较大且该方法具有鲁棒性差等缺点,极大地影响了两步法的标定精度,制约了两步法的实用性[4]。因此,在详细分析该两步法存在的问题后,结合人工鱼群算法(Artificial Fish Swarms Algorithm,AFSA)对两步法的不足进行优化,以此提高该方法用于星敏感器光学误差标定的精度。
1 两步法标定原理
根据星敏感器的小孔成像模型,在考虑主点位置偏差但忽略星敏感器测量噪声和光学畸变的情况下,第i(i=1,…,N)颗恒星对应的单位测量矢量可表示为

(1)
式中:(xi,yi)为第i颗恒星在星敏感器成像平面坐标系中的坐标;(Xc,Yc)为成像平面坐标系主点的坐标。
在天球坐标系中,导航星i对应赤经和赤纬坐标(αi,δi),在导航星表中与之对应的星光矢量可表示为
(2)
理想情况下,测量的星光矢量ωi与ωj的夹角和导航星表中对应的星光矢量νi与νj的夹角应该是相等的,有如下关系
sinθi j=|νi×νj|=|ωi×ωj|。
(3)
相对于常用来进行误差标定的星角距余弦值,在小角度计算时,正弦值有着比余弦值更敏感的感知,因此使用正弦值进行计算将会得到更高的精度[5]。
考虑光学畸变并结合式(1)、式(3)可得
(4)
式中,

(5)
(δxi,δyi)为星点i(xi,yi)的光学畸变量,x′i=xi-δxi,y′i=yi-δyi。


(6)
由于一般星敏感器工作状态下正常视场内的导航星数目大于3,则可得到超定方程组
(7)


(8)
bk+1=bk+Δbk
(9)

光学畸变包括径向畸变和切向畸变等[6]。径向畸变引起的图像点沿径向变化且对星敏感器标定影响较大,而其他畸变误差源的影响非常小且可忽略[7]。因此,在考虑光学畸变时仅考虑径向畸变引起的畸变量,取一阶径向畸变,得到光学畸变的近似式为
δx=q1xr2
(10)
δy=q1yr2
(11)
将式(10)、式(11)写作如下形式
(12)
式中:(xqi,yqi)为实际星点位置;(xi,yi)为理想星点位置;q1为一阶径向畸变系数。
假设有m个星点,结合式(3)、式(12)可得
D·q1=d
(13)

对式(13)求解最小二乘法可得
q1=(DTD)-1DTd。
(14)
以上标定原理用于星敏感器光学误差参数估计,基于星角距正弦值建立的方程和两步法迭代思想,操作如下:
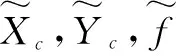
该方法流程如图1所示。

图1 两步法标定流程图Fig.1 Flow chart of two-step calibration
该光学误差标定方法利用正弦值建立观测方程,对小角度变化十分敏感,因此,相比余弦值更有助于标定精度的提高,并且通过不断迭代以同时完成主点、焦距以及一阶系数的标定,符合实用的快速和一体化的要求。但由于该方法使用最小二乘法进行估计,初值对标定速度、精度甚至算法的鲁棒性的影响都较大[8]。
2 基于AFSA算法的初值问题优化方法
为了克服两步法的初值问题,结合AFSA算法对初值要求不高、具备较好的全局寻优能力且能快速跳出局部最优解的特点,引入AFSA算法来得到一个较优的初值从而优化两步法的初值问题。
首先简单介绍一下AFSA算法的各项参数。有总数为N的人工鱼群,人工鱼个体的状态X=(x1,x2,…,xn)(xi(i=1,2,…,n)为寻优的变量),人工鱼移动的最大步长Sstep以及视野Vvis,尝试次数Ttimes、拥挤度因子δ、人工鱼个体i,j之间的距离di j=|xi-xj|,人工鱼当前所在位置食物浓度表示为Y=f(x)(Y为目标函数值,又称适应度)、人工鱼各种行为函数以及评价函数,rand()是0~1之间的随机数[9]。
人工鱼群算法是一种基于模拟鱼群行为的优化算法,人工鱼个体更新其状态主要靠以下4种行为。
1) 觅食行为。觅食行为主要就是在寻优过程中向着较优方向进行迭代,依靠人工鱼Xi的虚拟视野(如图2所示),在其视野内随机选择一个状态Xj

图2 人工鱼的视觉概念图Fig.2 Visual concept map of artificial fish
Xj=Xi+rand()·Vvis
(15)
比较它们的适应度函数值,如果发现Yj比Yi优,则人工鱼Xi向Xj的方向移动一步,触发前进条件
(16)
否则在视野内重新随机选择状态Xj,判断是否触发前进条件,若在Ttimes次后仍无触发前进条件,则触发随机移动条件,使Xi到达一个新的状态,即
Xnext=Xi+rand()·Sstep。
(17)
2) 聚群行为。人工鱼Xi探索当前视野内(di j (18) 否则执行觅食行为。 3) 追尾行为。追尾行为指的是人工鱼向其视野区域内最优个体的方向移动的一种行为,人工鱼Xi探索当前视野内(di j (19) 否则执行觅食行为。 4) 随机行为。随机行为是觅食行为的一个缺省行为,表示人工鱼Xi在虚拟视野内会向食物更多的方向快速且随机移动,到达状态Xnext,即 Xnext=Xi+rand()·Vvis。 (20) AFSA算法求解较优初值的过程如下所述。 1) 人工鱼群的产生。 Q={X1,X2,…,XN} (21) 式中,人工鱼Xi=(XciYcifi)T。 2) 计算目标函数。 目标函数实际上是用于评价优劣的适应度函数,使得误差补偿后的星点实际坐标(x′i,y′i)尽可能地接近理想坐标(xi,yi)是星敏感器光学误差标定的目的,所以可以定义目标函数为 (22) 式中,f(Xi)为人工鱼Xi的适应度。 3) 人工鱼数据更新。 在初始化后经过适应度计算取得最优人工鱼的状态并赋值给公告牌,对每条人工鱼个体进行行为评价,选择应执行的行为(包括觅食行为fPrey()、聚群行为fSwarm()、追尾行为fFollow()、随机行为fMove()),按照式(15)~(20)更新每条个体后生成新鱼群,并使用评价函数fEvaluate()来评价所有个体,将优于公告牌的状态更新到公告牌上。 4) 算法终止条件。 当公告牌上最优解的适应度函数小于给定精度,或者迭代次数Iite超过最大迭代次数IiteM时,算法终止。 人工鱼群算法的流程如图3所示。 图3 人工鱼群算法流程图 仿真实验所采用的星敏感器相关参数如表1所示。 表1 星敏感器性能指标Table 1 Star sensor performance indexes 相关仿真参数会根据实际的星敏感器型号进行针对性设计,星敏感器参数设置为:主点标准值Xc=1.00 mm,Yc=1.00 mm,焦距标准值f=43.56 m。根据经验得参考指标如下:主点偏差在10个像素以内,这里取0.15 mm,则主点真实值为(1.15,1.15)(单位,mm);焦距偏差在0.02倍的理想焦距内,对应焦距真实值为44.43 mm;选择镜头一阶畸变系数的真实值为q1=5×10-4。同时为消除光学畸变耦合对焦距标定的影响,根据文献[10]的结论,将星光入射角范围限制在入射角阈值βmax内。 首先需要验证初值设置对两步法标定是否有较大影响,为此选择真实值附近的20组初始值来进行两步法迭代,经过40次的迭代输出主点、焦距和一阶畸变系数的标定结果,通过对比仿真图中数据的变化大小来判断初值的不同对标定结果产生的影响大小。仿真数据结果见图4。 图4 不同初值条件下两步法标定结果Fig.4 Calibration results of the two-step method under different initial conditions 由图4可知:对于不同初始值输入得到的标定结果差别较大,表明对于星敏感器光学误差标定来说,两步法在处理参数多且非线性耦合的光学误差标定问题上有着显著缺点,易受初值设定影响,使得标定结果不稳定,且容易被困在局部最优中无法得到更优解,导致标定的可靠性受到影响,鲁棒性较差。 仿真验证人工鱼群算法计算初值后代入两步法标定中可以优化两步法的不足,在进行仿真初始化时,将AFSA算法的最大迭代次数设置为300,人工鱼的个体数量N=30、感知距离Vvis=25 mm、移动的最大步长Sstep=3 mm、觅食行为的尝试最大次数Ttimes=50,人工鱼群的拥挤度因子δ=27以及适应度函数的精度阈值设置为10-3,当公告牌上最优人工鱼对应的适应度函数值小于精度阈值,则迭代终止。仿真结果如图5所示。 图5 人工鱼群算法计算光学误差各参数初值结果Fig.5 Initial values of optical errors calculated byartificial fish swarm algorithm 由图5可知,使用人工鱼群算法计算用于代入两步法的初值的结果在迭代91次左右之后趋于稳定,得到的x轴主点参数初值是1.147 13 mm,y轴主点参数初值是1.148 85 mm,焦距初值为44.636 1 mm。对比仿真设置的对应真实值(1.15 mm,1.15 mm,44.43 mm)发现,使用人工鱼群算法得到的值与真实值比较接近,甚至在精度要求一般的情况下可以作为光学误差标定的结果来输出,由此可见,人工鱼群算法的全局搜索能力能够跳出局部最优,搜索出一组非常接近真实值的全局最优解,从而作为初值代入两步法中进行标定,进而提升两步法标定的精度,增强其算法的鲁棒性。 得到人工鱼群算法计算出的初值后代入两步法,得到仿真结果如图6所示。 图6 基于人工鱼群算法的两步法光学误差各参数标定结果 通过人工鱼群算法提供初值的两步法标定的仿真结果如下:x轴主点位置的标定结果为1.139 7 mm,y轴主点位置为1.123 8 mm,焦距的标定结果为44.442 7 mm,一阶畸变系数的标定结果为3.983 8×10-4,标定结果同实验初始设置的真实值相比,x轴主点的标定误差是0.010 3 mm,y轴主点的标定误差是0.026 2 mm,焦距的标定误差为0.011 5 mm,一阶畸变系数的标定精度为1.016 2×10-4。 通过对比标定结果可知,利用人工鱼群算法的全局搜索能力来得到一个较优解,并作为初值代入两步法中弥补两步法易受初值影响的不足,通过输入一个较优的初值并利用两步法局部寻优的特性,最终可计算得到具有较高精度的光学误差参数的估计值。 本文以星敏感器的光学误差对测量精度影响较大为起点,针对星敏感器光学误差标定方法中两步法的不足,提出了一种利用人工鱼群算法为两步法提供初始输入的改进方法。改进的两步法利用了人工鱼群算法对初值要求不高、具有全局寻优能力、解算速度较快和鲁棒性强的特点,还利用了两步法本身局部寻优能力强的特点,先使用人工鱼群算法计算得到一个全局较优的解,再用该解作为初值代入两步法中,最终解算出标定结果。由仿真结果可知,该方法可较稳定地得到精度较高的标定值,同时可得到x轴和y轴主点坐标、焦距以及一阶畸变系数这4个参数的估计,该方法不依赖昂贵的地面标定设备,有着灵活的使用场景并且具备良好的可靠性。
3 仿真实验与结果分析
3.1 实验条件设计

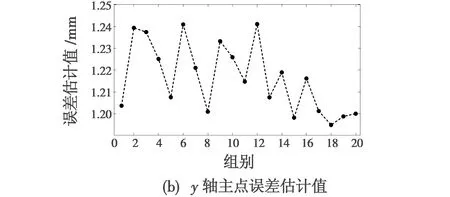
3.2 不同初值下的两步法标定仿真结果



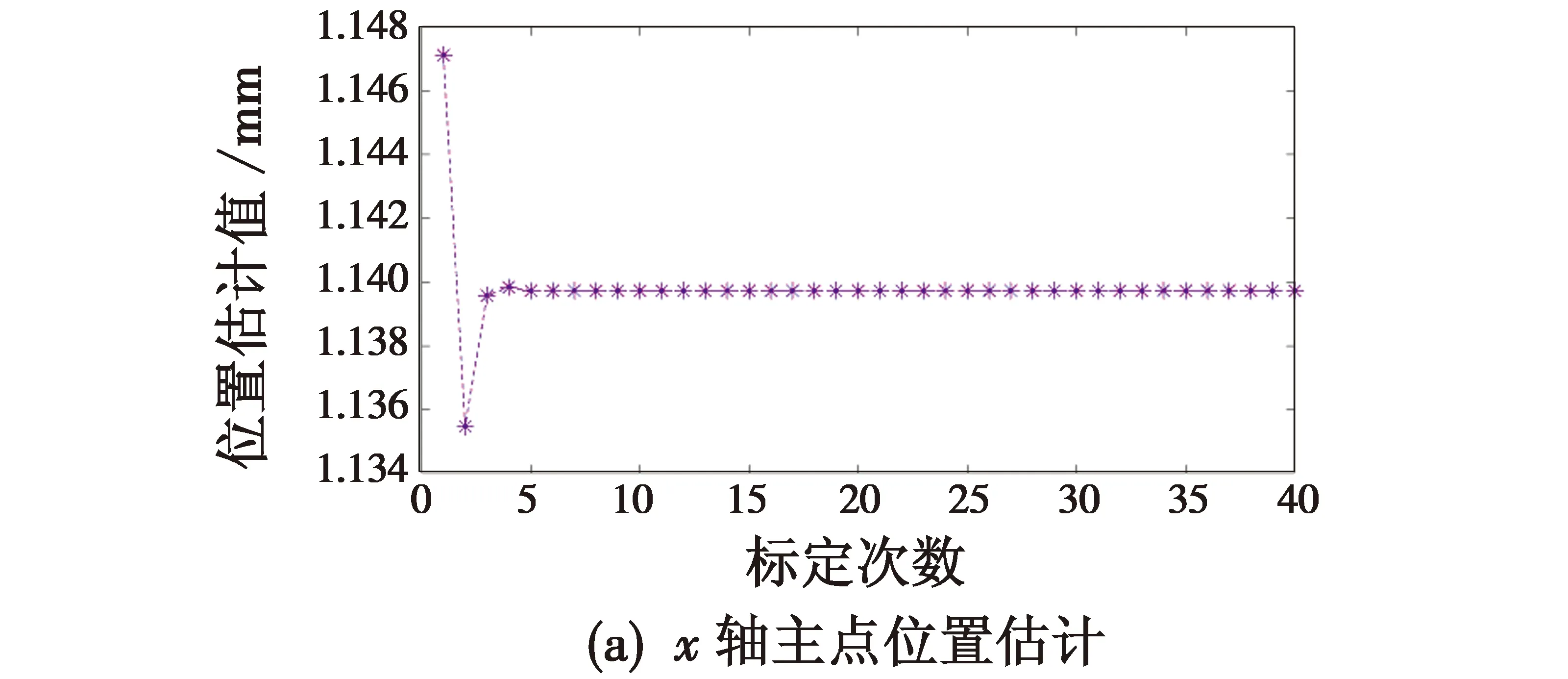
3.3 基于AFSA算法优化的两步法标定仿真







4 结论
