基于离散滑模控制的四旋翼飞行器轨迹跟踪
2022-04-07成利梅
成利梅
(太原科技大学,太原 030000)
0 引言
四旋翼飞行器具有呈“十”字交叉结构的4个旋翼,通过调节不同旋翼电机转速改变螺旋桨转速从而实现飞行器的运动。由于其特殊的结构,四旋翼飞行器可实现垂直起降并悬停,且能以各种姿态飞行,具有更强的机动性和灵活性,因此广泛应用于军事、电力巡检、农业植保等领域[1-2]。
BOUABDALLAH[3]首先建立了四旋翼飞行器的数学模型,并比较了PID、最优控制、反步控制和滑模控制等控制方法。鲁棒自适应[4]、自抗扰控制[5]等先进的控制方法也被应用于四旋翼飞行器的控制。然而,大多数的研究均采用欧拉角表示旋转矩阵,并用欧拉角的一阶导数近似载体角速度。基于近似模型设计的控制器仅适合于欧拉角较小的悬停状态,并不能应用于机动性要求较高的大角度飞行。为了解决大角度飞行的控制问题,LEE等[6-7]提出了几何控制。几何控制在非线性群SO(3)(Special Orthogonal Group)上描述飞行器的动力学模型,并基于此模型设计控制律。文献[8-10]对基于该模型的轨迹跟踪控制算法进一步研究,结果表明,基于SO(3)的动力学模型设计控制器可使得四旋翼飞行器完成较为复杂的运动。
在实际控制过程中,都需要微处理器进行实时采样和计算,因此,近年来基于离散时间域的四旋翼飞行器控制算法引起了广泛研究。但目前大多数的研究都是基于欧拉角模型的轨迹跟踪控制[11-13],或者是基于非线性群SO(3)的姿态控制[14-16]。针对这一现状,本文基于非线性群SO(3)上的动力学模型设计基于离散时间域的轨迹跟踪控制器。同时考虑到滑模变结构控制对参数的不确定性以及有界干扰都具有良好的鲁棒性[17],本文将离散滑模变结构控制律应用于控制器的设计,以提升控制效果。
1 动力学建模
为了方便建模,假设四旋翼飞行器的机械结构对称,并且可以看作刚体。在四旋翼飞行器的运动控制中,位置和姿态都是至关重要的信息。描述刚体的位置与姿态时,首先需要确定刚体所在的坐标系(参考坐标系),同时刚体上任何一点可以通过与其固连的坐标系(载体坐标系)描述,因此在四旋翼飞行器的动力学建模之前,需先引入两个坐标系,即参考坐标系{xwywzw}和载体坐标系{xbybzb},所定义的坐标系如图1所示,图中Ω1~Ω4为4个电机的转速。

图1 四旋翼飞行器结构及对应坐标系
基于所定义的坐标系,采用牛顿-欧拉法对四旋翼飞行器进行建模[18],所建立的数学模型为
(1)
式中:向量p=[xyz]T,为四旋翼飞行器质心在参考坐标系中的位置;ω=[ω1ω2ω3]T,为四旋翼飞行器在载体坐标系下的角速度;R∈SO(3),为所定义载体坐标系到参考坐标系的旋转矩阵;向量zw=[001]T;m是四旋翼飞行器的质量;g是重力加速度;J为转动惯量;T为4个电机的升力和;M=[M1M2M3]T,为转动力矩。
在设计控制器之前,采用前向欧拉法将四旋翼飞行器的动力学模型进行离散化,离散化之后的模型为
(2)
式中,Δt为采样时间。
2 控制器设计
综合式(1)和式(2)可知,四旋翼飞行器的模型为强耦合、欠驱动的非线性系统。当位置确定之后即可确定姿态矩阵的第3列。同时,当偏航角和姿态矩阵的第3列均已知时,旋转矩阵即可被唯一确定[18]。当旋转矩阵确定之后,角速度可由旋转矩阵确定。因此,可以将位置和偏航角作为系统的控制目标。
由上述分析可知,位置的实现依赖于旋转矩阵的实现,因此本文将四旋翼飞行器的控制系统分为位置控制环路与姿态控制环路,位置控制环路输出控制升力的大小及方向,控制升力方向向量与期望偏航角经运算得出的期望旋转矩阵作为姿态控制环路的输入,姿态控制环路输出控制力矩,控制升力和控制力矩作用于四旋翼飞行器的数学模型,从而实现控制。整体的控制结构如图2所示。

图2 控制结构框图Fig.2 Block diagram of control structure
2.1 位置控制器设计
首先,基于离散滑模变结构控制律来设计位置控制器,定义k时刻的滑模面为
(3)
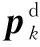
由式(3)可得k+1时刻的滑模面为

(4)
基于一阶趋近律可设计滑模面
sk+1=(I-kΔt)sk-ηsgn(sk)Δt
(5)
式中:I为单位阵;sgn()为符号函数;k和η为正定的对角阵,其中,k=diag(k1,k2,k3),η=diag(η1,η2,η3)。
令式(4)和式(5)相等,可得

(6)
将式(2)代入式(6),整理可得控制升力的大小为
(I-kΔt)Δtsk+ηsgn(sk)(Δt)2)/(Δt)2+mgzw)·(Rkzw)。
(7)
同时,控制升力的方向为
(8)
若设计升力如式(7)和式(8),则该系统在有限时间内可收敛于位置误差的零平衡点。
证明:由于3个方向结构相同,因此以其中一个方向为例来证明所设计控制器的稳定性[19],记sk=[sk,1sk,2sk,3]T,选取李雅普诺夫函数
(9)
由于
(10)
其中
(sk+1,i-sk,i)sgn(sk,i)=
((1-kiΔt)sk,i-ηisgn(sk,i)Δt-sk,i)·sgn(sk,i)=
(-kiΔtsk,i-ηisgn(sk,i)Δt)·sgn(sk,i)=
-kiΔt|sk,i|-ηiΔt<0
(11)
(sk+1,i+sk,i)sgn(sk,i)=
((1-kiΔt)sk,i-ηisgn(sk,i)Δt+sk,i)·sgn(sk,i)=
((2-kiΔt)sk,i-ηisgn(sk,i)Δt)·sgn(sk,i)=
(2-kiΔt)|sk,i|-ηiΔt
(12)

2.2 姿态控制器设计
旋转矩阵可由列向量表示为Rk=[xb,kyb,kzb,k],其中,zb,k可由式(8)给出,若给定偏航角ψd,当参考坐标系按照Z-X-Y旋转到载体坐标系时,期望旋转矩阵[18]则为
(13)
式中,xf,k=[cosψd,ksinψd,k0]T。
首先定义旋转矩阵误差为
(14)
当实际载体坐标系趋近于期望载体坐标系时,Re,k趋近于单位阵。同时由文献[20]可知,旋转矩阵R的特性主要由R-RT决定,且R-RT为反对称矩阵,因此可以用R-RT的向量形式表征R的特性。基于此,定义表征旋转矩阵误差特性的向量
(15)
式中:ε为正定的对称阵,ε=diag(ε1,ε2,ε3);运算符·∨表示将反对称矩阵写成其所对应的向量形式。当Re,k趋于单位阵时,eR,k则趋近于0。
基于旋转矩阵误差,定义角速度误差为
(16)

基于旋转矩阵误差的向量形式和角速度误差,设计k时刻的滑模面为
(17)
式中,β=diag(β1,β2,β3),为正定的对角阵。
由式(17)可得k+1时刻的滑模面为
sk+1=βeR,k+1+eω,k+1=
(18)
基于一阶趋近律设计如下滑模面
sk+1=(I-λΔt)sk-γsgn(sk)Δt
(19)
式中,λ和γ为正定的对角阵,λ=diag(λ1,λ2,λ3),γ=diag(γ1,γ2,γ3)。
令式(18)与式(19)相等,可得

(20)
将式(2)代入式(20),整理可得控制力矩为
Mk=J((I-λΔt)sk-γsgn(sk)Δt-β(ε(Re,k+1-
(21)
若设计控制力矩如式(21),则姿态控制环路在控制力矩M的作用下可使得系统渐近稳定。
证明:由于3个方向结构相同,因此以其中1个方向为例来证明所设计控制器的稳定性,记sk=[sk,1sk,2sk,3]T,选取李雅普诺夫函数
(22)
由于
(23)
其中
(sk+1,i-sk,i)sgn(sk,i)=
((1-λiΔt)sk,i-γisgn(sk,i)Δt-sk,i)·sgn(sk,i)=
(-λiΔtsk,i-γisgn(sk,i)Δt)·sgn(sk,i)=
-λiΔt|sk,i|-γiΔt<0
(24)
(sk+1,i+sk,i)sgn(sk,i)=
((1-λiΔt)sk,i-γisgn(sk,i)Δt+sk,i)·sgn(sk,i)=
((2-λiΔt)sk,i-γisgn(sk,i)Δt)·sgn(sk,i)=
(2-λiΔt)|sk,i|-γiΔt
(25)

当采用滑模控制律时,不可避免地会给系统引入振颤。为了减少振颤,本文采用饱和函数来代替符号函数。
3 仿真验证
通过Matlab/Simulink来仿真验证所设计系统的有效性[22]。为了验证所设计的控制律可使得四旋翼系统实现大角度的飞行,选取侧立圆为期望轨迹。设pd=(0.5cos 2t0.5sin 2t3-2cos 2t)T,期望偏航角为ψd=t,四旋翼的初始状态为p(0)=(000)T和ψ(0)=0。仿真所采用的结构参数为m=2.0 kg,J=diag(1.25,1.25,2.5)。
文献[21]通过仿真实验详细研究了控制参数对系统动态响应以及控制输入的影响,在此基础上结合仿真实验选取本文仿真过程中的控制器参数,所采用的控制参数如表1所示。
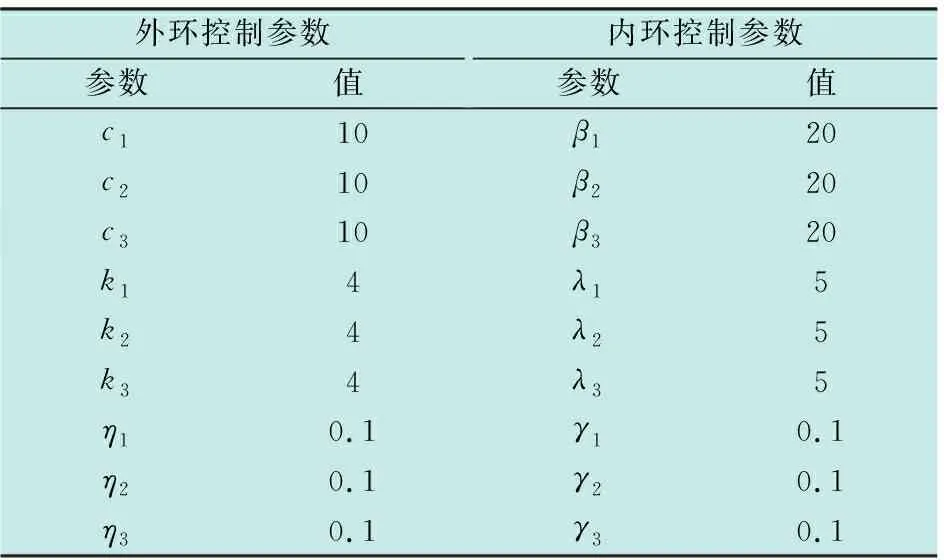
表1 控制器参数Table 1 Controller parameters
若采样时间Δt为0.01 s,采样点数为4000,仿真结果如图3所示。

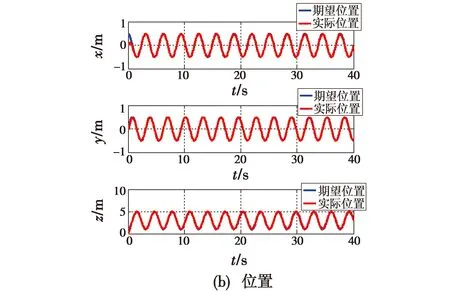

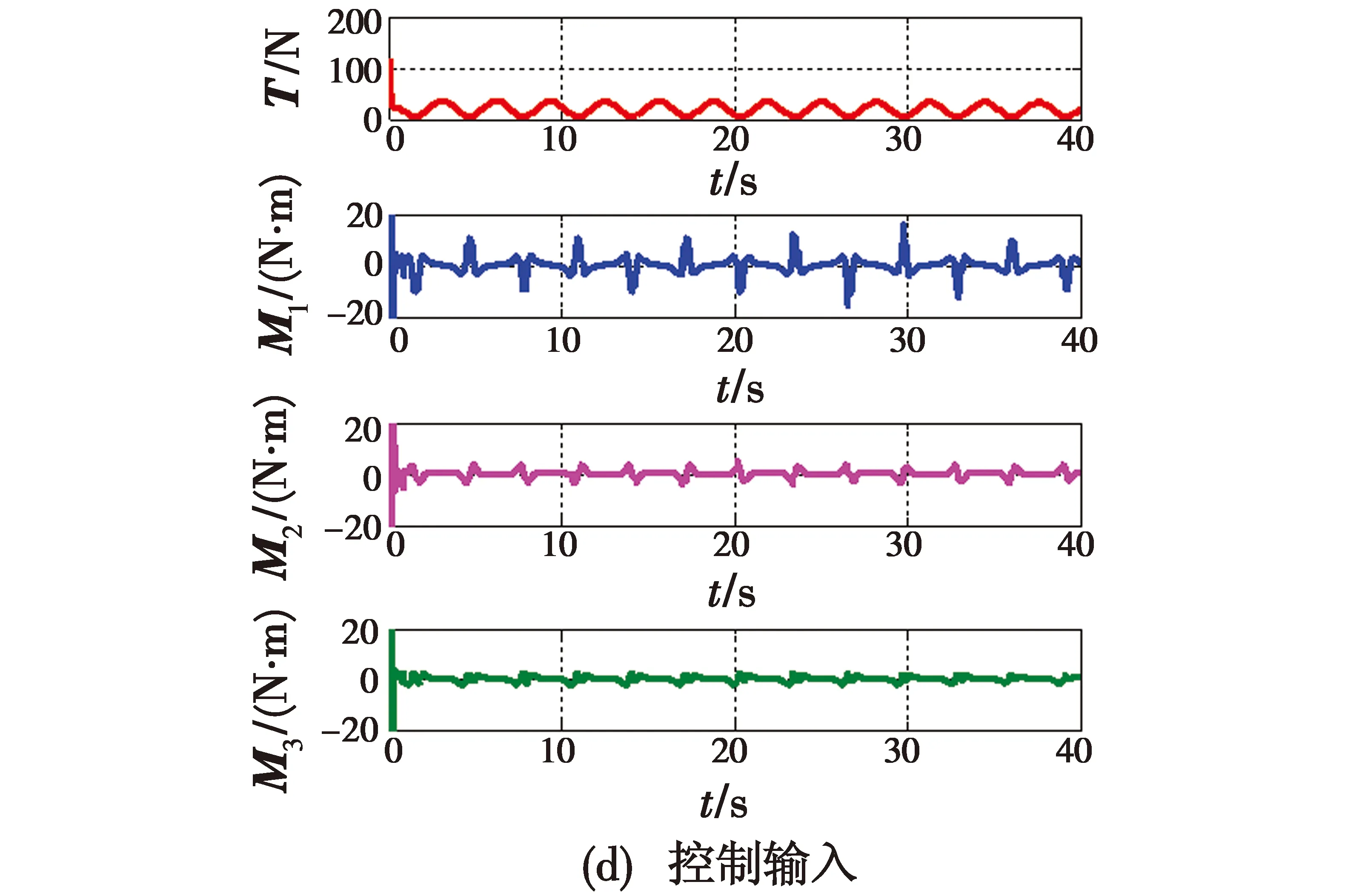
图3 四旋翼飞行器跟踪侧立圆仿真结果
图3(a)和图3(b)分别为跟踪侧立圆时的三维轨迹和位置图,由图可知,系统在所设计控制律的作用下能很快跟踪上期望轨迹。图3(c)描述了期望欧拉角与实际欧拉角,欧拉角(φ,θ,ψ)由旋转矩阵计算得出。从图中可得,实际欧拉角很快收敛于期望欧拉角。此时,实际的旋转矩阵也将趋于期望的旋转矩阵。由于偏航角ψ的取值范围为(-180°,180°),因此偏航角仅在该范围内周期变化。图3(d)为控制输入图,由图可知,T以期望轨迹的周期变化,M1,M2和M3呈现相似的变化趋势,仅在姿态发生突变时发生较大的突变,在其他时刻很快收敛到0。综合图3(a)和图3(c)可知,所设计的控制系统可实现大欧拉角的轨迹跟踪。
4 结束语
本文针对离散时间域的四旋翼飞行器轨迹跟踪控制问题进行研究。基于非线性群建立了动力学模型,解决了采用欧拉角近似建模带来的小角度飞行限制,可使得四旋翼实现大角度飞行。由于四旋翼飞行器系统的强耦合、欠驱动特性,设计了基于内外环的控制结构,内外环控制器均采用离散滑模变结构控制来设计。仿真实验表明,在所设计控制器的作用下,四旋翼飞行器可以实现大角度的轨迹跟踪,验证了所设计系统的有效性。
