T-S模糊半马尔可夫跳变系统故障估计
2022-04-07朱永宁李晓航
朱永宁, 李晓航
(上海工程技术大学,上海 201000)
0 引言
马尔可夫跳变系统(MJS)是一种具有多个模态或子系统的混杂动态系统,在过去几十年中,MJS已经在工业生产[1]、航空航天[2]、网络通讯、社会经济等领域中有着广泛的应用。与要求驻留时间服从指数分布的MJS不同,半马尔可夫跳跃系统(S-MJS)的驻留时间分布更具一般性,比如Weibull分布。由于放松了驻留时间的分布条件,半马尔可夫跳变系统在工程应用中具有更广阔的应用场景。
执行器故障和传感器故障在实际工程的控制系统中经常出现,现阶段,控制领域针对MJS的故障检测和容错控制[3-5]、状态和故障估计[6-9]的研究获得了很大进展。其中,基于状态观测器的故障诊断方法是指在获得系统的数学模型情况下,通过输出的估计值与测量值生成残差信号判断系统是否存在故障。文献[6]设计一种滑模观测器,研究了Lipschitz MJS传感器故障估计和容错控制问题。针对一类考虑执行器故障的MJS,文献[7]利用滑模控制技术研究了有限时间有界性问题。然而,实际应用中执行器和传感器故障往往同时发生,因此,针对执行器和传感器故障同时估计的研究具有更实际的应用价值。同时,由于对MJS或S-MJS的研究大多数都假设其状态转移概率(TRS)是完全已知的[10],这在实际应用中具有很大的局限性,因此,将现有的故障估计理论推广到更为一般的不确定转移概率S-MJS中,具有更实际的应用价值。
另一方面,故障估计理论在实际非线性系统中的应用具有一定的局限性。Takagi-Sugeno(T-S)模糊模型基于一组IF-THEN的规则,其方便简单的优点,可以使现有的故障估计方法在非线性系统中得到较好的应用。目前,针对T-S模糊系统的故障估计研究取得了很多成果。例如,文献[11]利用T-S模糊模型,设计了一种比例积分观测器(PIO),能够对一类不确定非线性系统进行执行器故障估计和容错控制;文献[12]针对一类状态转移概率已知的T-S模糊MJS故障估计问题,设计了一种自适应观测器;文献[13]针对一类一般不确定状态转移概率的MJS,设计了一种能够同时估计执行器和传感器故障的降维观测器,然而,该观测器并不能完全消除外部干扰造成的影响。
综上所述,本文针对一类T-S模糊S-MJS设计了一种降维观测器。该观测器具有以下优点:在较为宽松的前提下,能够完全解耦外部干扰,有效避免了外部干扰造成的影响;能够同时估计执行器和传感器故障,且不用获取故障及其导数上界[6],并保证误差系统在有限时间内稳定;部分已知转移概率的S-MJS,更具有一般性。
1 系统描述
考虑带有执行器和传感器故障的S-MJS,用如下T-S模糊模型表示。
规则α:若θ1(t)是να1,且θq(t)是νaq,则
(1)

(2)

基于标准模糊规则,S-MJS模糊系统为
(3)


转移概率矩阵Π可以表示为
(4)
式中,“?”表示不可测元素。

(5)
定义1对于式(3)系统,如果u(t)≡0,d(t)=0,存在常数c1,c2,T>0,以及正定矩阵Hi,有
Ε{xT(0)Hix(0)}≤c1⟹Ε{xT(t)Hix(t)}≤c2∀t∈[0,T]
(6)
成立。式中,0
假设1 假设Gi和Ki是列满秩,Ci是行满秩。
假设2
(7)
引理1假设ε代表任意实数,C代表任意矩阵,当D>0时,不等式
ε(C+CT)≤ε2D+CD-1CT
(8)
成立。
引理2假设ν(t)为非负函数,若

(9)
那么对于常数a,b≥0,可得
ν(t)≤aebt0≤t≤T。
(10)

(11)
(12)

(13)
2 降维观测器设计
式(3)系统等价于
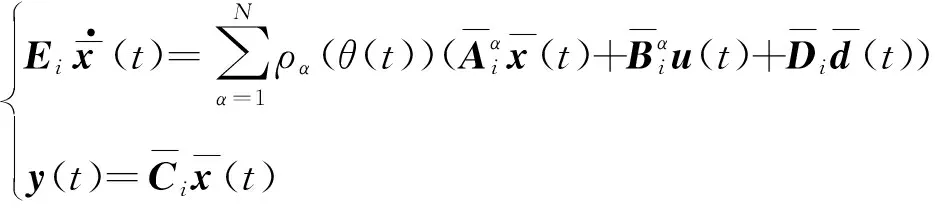
(14)
(15)

(16)
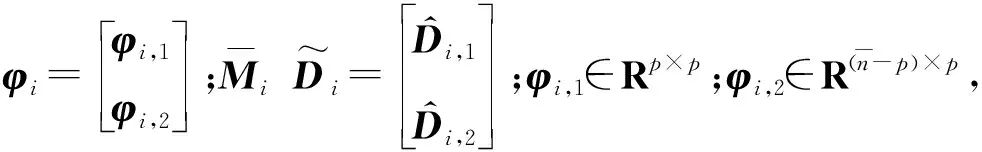
(17)
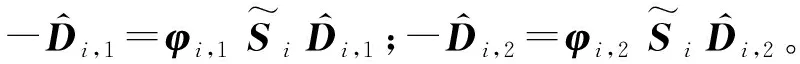
(18)


(19)
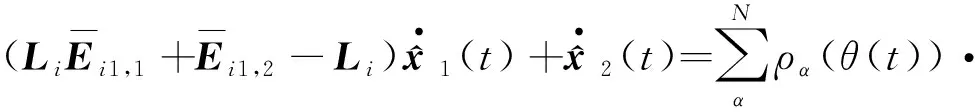
(20)
式中:
(21)


(22)
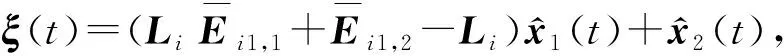

(23)
设计降维观测器为
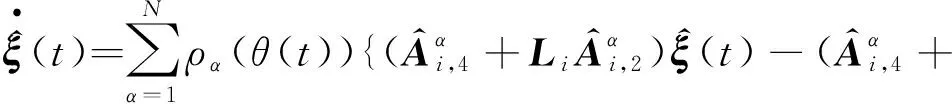
(24)
式中:
(25)

3 主要结论


(26)
(27)
(28)
(29)

(30)

(31)

(32)
根据引理1,可得
(33)
最终得到

(34)
对于∀i,j∈S,当i≠j,λi j(h)≥0,i=j,λi j(h)<0,讨论下面两种情况:


所以存在α>0,使得
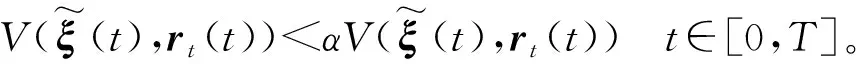
(35)
对式(35)使用Dynkin’s公式,得到

(36)
根据引理2,可以得到
(37)
(38)
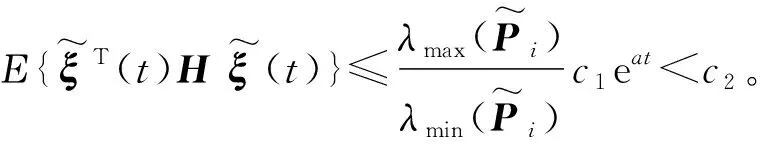
由此可以得到式(25)误差系统是有限时间随机稳定的,定理1的证明结束。
根据定理1,可以得到如下状态和故障估计

(39)
4 仿真
为了证明本文所提方法的有效性,考虑如下具有3个模态的数值T-S模糊半马尔可夫跳变系统,相关参数如下:


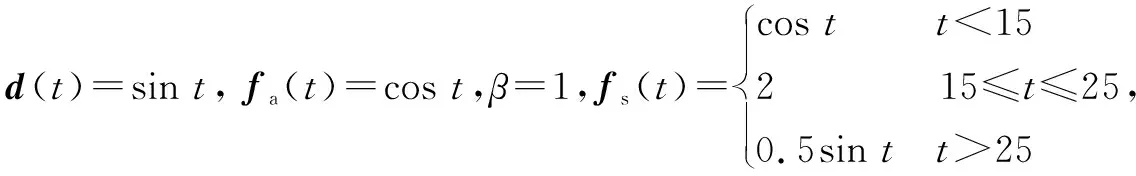
图1为系统的实际状态和估计状态的对比曲线,图2(a)和图2(b)分别为执行器故障和传感器故障估计曲线,图2(c)为系统状态x的估计误差曲线,图2(d)为执行器和传感器故障的估计误差曲线。综合图1~2,本文所设计的降维观测器能够同时估计系统状态、执行器故障、传感器故障,消除外部扰动的影响,保证误差系统的有限时间稳定。


图1 系统状态及其估计值Fig.1 System states and their estimations



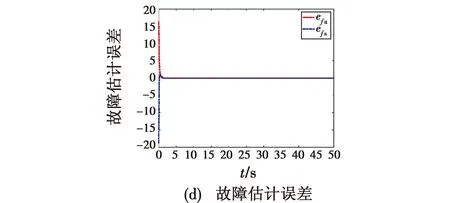
图2 仿真结果Fig.2 Simulation results
5 总结
本文针对一类具有一般不确定转移速率的T-S模糊半马尔可夫跳变系统的执行器故障和传感器故障同时估计问题,设计了一个降维观测器。该观测器在较为宽松的前提下,可以完全解耦外部扰动,同时估计执行器故障和传感器故障。借助线性矩阵不等式给出观测器存在的充分条件,进一步证明其有限时间稳定性。最后,通过一个数值仿真验证了所提方法的有效性。
