基于ITAE的舰载火箭炮位置控制器设计

2022-04-07王攀伟侯远龙

电光与控制 2022年4期

王攀伟，侯远龙，吴亮

(南京理工大学机械工程学院，南京 210000)

0 引言

舰载火箭炮以舰船作为发射平台，当舰船在大洋中行驶时，会受到海浪、洋流、大风等因素的综合作用,使舰船产生纵摇和横摇，剧烈的纵横摇运动使舰载火箭炮的定向管产生偏差，严重影响火箭炮的射击精度,因此舰载火箭炮的稳定控制研究是提高火箭弹射击精度的关键[1-2]。ITAE(时间与误差绝对值乘积积分)三阶无静差控制方法提出的时间很早，1953年，美国学者GRAHAM和LATHROP就已经用模拟计算机计算出各阶线性系统在满足ITAE最优时应具有的参数[3-4]。目前，国内对ITAE的研究较少，其中，项国波[3]是国内最早研究ITAE控制的，首先将ITAE控制方法应用于工程实践中并获得良好的控制效果。随着智能控制方法的发展，将智能控制和ITAE控制相结合形成新的研究方向。舰载火箭炮用永磁同步电机作为驱动元件，永磁电机本身就具有复杂的非线性因素，同时在火箭炮发射时，其负载力矩和转动惯量也会发生改变，使系统的结构参数发生改变。因此，如何更好地对系统模型进行辨识是控制器设计中的关键。近年来，不断有学者针对舰载火箭炮的系统辨识问题提出新的解决方法，如遗传算法、NSGA-II算法、粒子群优化算法、差分进化算法以及一些混合智能算法等，但是这些算法均需要大量计算，对于实时性要求较高的舰载武器，需要更加简便的控制算法。因此，本文结合工程实践提出用M序列辨识系统脉冲响应函数，进而求出系统参数的方法。在实验台架上进行实验研究，结果表明所提控制方法具有良好的动态性能和跟踪精度。

1 ITAE最佳传递函数

已知，一个调节量的系统在主动和干扰激励下，其动态响应的微分方程为[5]

(1)

式中：c(t)为作用量；g(t)为主动激励；f(t)是干扰激励；ai，bj，lk是系统参数系数。由式(1)可知，被控参数状态变化的响应过程由主动激励和干扰激励组成，系统响应的目标为：对控制来说，希望c(t)准确跟着g(t)的变化；对扰动而言，希望c(t)不受f(t)的影响。因此在理想情况下要求

(2)

满足式(2)的条件，就有

(3)

的结果，称这样的系统为“不变性”系统。在这样理想系统中，误差任何时刻都是零。现实中，所有实际使用的具体系统，都需要进行能量转换和传递，并且能量转换和传递过程是需要一段时间的，尽管这个时间很短。所以误差的时间函数e(t)总是存在的，并且是消除不了的。因此对式(1)的要求，只能是尽可能多的低阶系数相等，即

(4)

对应于式(4)的条件，对误差的要求只能是

|e(t)≥0|或e2(t)≥0

(5)

式中，符号“≥”表示大于但是趋近于零。

因此，如果|e(t)|或e2(t)在系统响应的过程中，时刻都满足式(5)中的条件，那么系统的性能就与理想系统的性能接近。因为不论哪种激励产生的动态响应，都可以用误差来表示，所以e(t)就变成评判系统性能的一种广泛使用的标准。因为误差的值是时刻在变化的，把它作为系统的评价标准会带来很多不便，因此在工程应用上，评价系统性能的好坏，一般使用误差的积分大小，即性能指标积分评价函数[6]

(6)

式(2)、式(4)指出，满足ITAE极小值原则的最佳系统的研究，也就是确定描述该系统动态过程方程式各阶系数取何值，以及左右两侧系数相等到哪一阶n，才能得到ITAE极小值。

目前，数字计算机在工程实践中得到了大量使用，但在一个调节量的系统中，使用传递函数法仍比空间状态法方便。令式(1)中f(t)=0,并且假定系统各阶导数的初始状态为零。对式(1)做拉普拉斯变换，系统在主动激励信号G(p)作用下的闭环传递函数为

(7)

式中：C(s)和G(s)分别表示c(t)和g(t)的拉普拉斯变换；s为拉普拉斯变换的算子。

由经典控制方法可知，要使系统具有一阶无静差，即对位移输入无静差，系统的闭环传递函数为

(8)

即s的零阶系数相等。

对二阶无静差系统，即对匀速输入而言，系统的闭环传递函数为

(9)

即s的一阶以下系数相等。

对三阶无静差系统，即对匀加速输入而言,系统的闭环传递函数为

(10)

即s的二阶以下系数相等。式中，an-i=ai/an,i=0,1,2,…,n-1。

按照逻辑推理，随着给定输入t的阶n的增加，传递函数分母、分子的s的阶n的系数相等项也要相应增加，才能保证系统具有相应阶n的无静差度。令an=ω0，p=s/ω0,则式(8)为

(11)

式中，βi=ai/ω0，i=1,2,…,n-1。

同理，式(9)为

(12)

同理，式(10)为

(13)

式(11)～(13)被称为标准化传递函数，但不是最佳的，因为静差只是动态品质指标之一，不是全部。但是有了这些标准化传递函数，就可以用来确定满足ITAE极小值的标准化系数βi，i=1,2,…,n-1。文献[4]给出这些公式(即式(11)～(13))满足ITAE极小值的系数βi。按照这种原则而得到的闭环系统传递函数被称为ITAE最佳调节系统的传递函数，简称为ITAE最佳传递函数。

2 ITAE控制器的实现

最佳传递函数确定之后，下一步的任务就是根据工艺要求和调节对象的传递函数，选择相应的最佳传递函数及其综合结构和参数。这里所谓的调节对象已经不是具体的生产对象，而是为控制这些对象而按力学规律确定的执行机构，这些机构通常是大功率的[7-8]。火箭炮的系统输入可以为阶跃输入；也可以为斜坡输入、抛物线输入；还可能是这3个量中的任意2个的结合；又或许是3个量同时输入，同时还有快速性的要求，因此，舰载武器系统应以ITAE三阶最佳传递函数为宜。

易知，舰载火箭炮系统调节对象为大惯性，不宜采用极-零点对消法，可以采用图1的结构。

图1 系统校正图Fig.1 System calibration

系统传递函数为

(14)

令KKzτTe≫1，得

(15)

有如下联立方程组

(16)

求解上述方程组，得综合结构的参数为

(17)

并且计算不等式KKzτTe≫1是否满足。把相关参数代入，得

KKzτTe=2.968T≫1。

(18)

结果说明这个方案适用于大惯性对象。通过上述分析可知，应用误差反馈法，匹配以其他调节器，可以得到匀加速无静差ITAE三阶最佳调节，这是其他常用的综合结构不容易实现的，因此是比较好的综合方法之一。

3 系统辨识

舰载火箭炮在工作时有很多非线性和随机成分，这些不确定成分致使火箭炮伺服系统参数发生变化。因此，控制系统必须能够根据调节对象参数的变化自动调节控制参数，本文提出位置环辨识框图，如图2所示。

图2 位置环辨识框图Fig.2 Block diagram of position loop identification

3.1 辨识原理

1) 伪随机二位式序列-M序列的产生及性质。

伪随机序列是一种很好的辨识输入信号，它和白噪声信号有类似的特点，不但可以获得很好的辨识结果，而且在实践中很容易获得。M序列即二位式最大长度线性反馈移位寄存器序列，是伪随机序列中最简单的一种，它由带有线性反馈逻辑电路的移位寄存器组成[9-10]。

通常移位寄存器由带有移位能力的触发器构成，如图3所示，其中，每一个图框代表一个寄存器，图框里的数字代表寄存器目前的输出结果(0或1)。在移位脉冲的激励下，寄存器的输出结果(an-1，an-2，…，an-r)向右移动一位，将各个寄存器中的部分状态进行模二相加，反馈到第一级的输入端an。

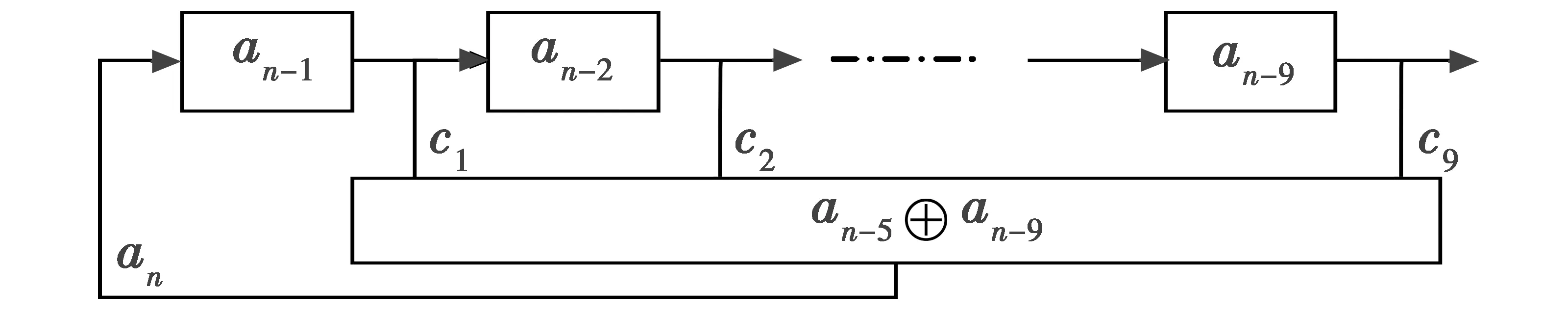
图3 随机序列发生器原理图Fig.3 Schematic diagram of random sequence generator

在上述脉冲的激励下，输出一个无限长的周期性二位式序列，an的通用表达式为

(19)

式中,⊕表示模二相加(半加或按位加，即1+0=1,0+1=1,1+1=0,0+0=0)。

2) M序列的自相关函数(Rx(τ))。

M序列“0”和“1”的两种状态相应地用大小为+a和-a的二电平序列表示，同时每一个电平的延迟时间为Δ，则M序列的周期是NΔ。在工程实践上，延迟时间Δ和电平大小a均采用固定值。在M序列中，因为“1”的个数比“0”的个数多1，所以，在一个序列周期中电平+a的脉冲数比电平-a的脉冲数多1。电平是-a的脉冲数为(N-1)/2，电平是+a的脉冲数为(N+1)/2。

经过计算易得

(20)

在N值特别大时，可得

(21)

由式(20)和式(21)可知Rx(τ)由周期性三角形脉冲和直流分量[11]两部分构成。

当Δ很小时，周期性三角脉冲可用理想脉冲函数代替，因此在1个周期中有

(22)

3) M序列辨识系统的脉冲响应函数。

对于线性定常单输入单输出系统，设x(t)为系统输入,y(t)为系统输出，g(t)为系统脉冲响应函数，则有

(23)

易得

(24)

即

(25)

为著名的维纳-霍夫积分方程[12]，它给出了自相关函数Rx(τ)、输入x(t)和输出y(t)的互相关函数Rxy(τ)以及脉冲响应函数g(t)之间的关系。如果已知Rx(τ)和Rxy(τ)，就可求出g(t)。

适当选择M序列周期T=NΔ，使得脉冲响应函数g(t)在t

(26)

代入M序列自相关函数表达式，有

(27)

式中的第2项不随τ而变化，记为常值

(28)

则有

(29)

3.2 相关辨识法的位置环自整定

位置环整定的基础是对速度环闭环传递函数的辨识。图2给出了相关辨识法位置环自整定框图，一般舰载火箭炮伺服系统的速度闭环传递函数可以看作一阶惯性环节

(30)

(31)

1) 伪随机序列的产生。

伪随机序列取r=9，ci(i=1,…,9)的取值为c5=1，c9=1，其余为零[13]。这时伪随机序列的周期为N=2r-1=511，状态反馈表达式an=an-5⊕an-9，并将伪随机序列的状态“0”变换成幅值+a，状态“1”变换成幅值-a。

2) 脉冲响应函数的计算。

为了辨识传递函数G(s)对应的脉冲响应函数，首先需要采集该传递函数的输入(M序列)和输出y(t)。输入输出量采样周期的选取与M序列时钟脉冲间隔Δ相同，τ为Δ的整数倍，则有

(32)

在每个时钟脉冲间隔中，近似有

(33)

因此有

τ=0,Δ,…,(N-1)Δ。

(34)

为了提高计算互相关函数的准确度，通过多输入几个二电平M序列，利用较多的输出值计算互相关函数,设输入(m+1)个周期二电平M序列，记录(m+1)周期输出的采样值，并由x(iΔ)=asgn[x(iΔ)]，

(35)

令

(36)

(37)

通过对输入输出采样由式(35)～(37)直接计算出

g′(t)=m·(N+1)aΔg(t)

(38)

max(g′(t))=m·(N+1)aΔmax(g(t))

(39)

而由式(39)易得

max(g(t))=K/T

(40)

因而有

max(g′(t))=(m·(N+1)aΔ)/T

(41)

有

(42)

4 实验分析

本文提出的控制方法通过实验台架来进行验证。实验中用到的永磁同步电机参数为：功率1.6 kW,最高转速为3600 r/min,连续堵转转矩为40 N·m,连续线电流为5.3 A,额定线电压为220 V,转动惯量为0.001 143 kg·m2。

1) 动态性能。图4(a)为系统在10°小阶跃时的误差曲线，图4(b)是系统310°大调转时的误差曲线。从图4中可以看出，小阶跃响应没有超调，而310°大调转的超调量为3.5%，调转时间为4.3 s,系统响应速度很快，超调量小。

图4 控制系统阶跃响应曲线Fig.4 Step response curves of the control system

2) 跟踪精度。图5所示为60 (°)/s等速跟踪的误差曲线，图6(a)为加速度7.5 (°)/s2的正弦跟踪时的误差曲线，图6(b)为45 (°)/s2的正弦跟踪时的误差曲线。由图6可以看出，60 (°)/s的等速跟踪最大误差为1.89 mil，加速度7.5 (°)/s2的正弦跟踪最大误差为0.8 mil，加速度45 (°)/s2的正弦跟踪最大误差为1 mil。所以，从正弦跟踪和等速跟踪上可以看出,本文提出的ITAE控制方法具有优良的跟踪性能，非常适合用于大功率武器系统的位置控制。

图5 60 (°)/s等速跟踪误差曲线Fig.5 Isokinetic tracking error at speed of 60 (°)/s

图6 正弦跟踪误差曲线Fig.6 Sinusoidal tracking error curve

由实验结果可知，系统在小阶跃调转时，没有超调，在大角度工作时，虽然会有一些超调，但是响应速度很快，符合舰载武器的性能要求。系统以60 (°)/s等速跟踪时，最大跟踪误差不超过2 mil，在大功率舰载武器系统中已经很不容易做到，由实验波形中的正弦跟踪过程可知，当加速度为45 (°)/s2时，最大误差不超过1 mil。这个加速度输入值远高于同时期的功率等级大体相当的武器系统，而且没有加入二阶前馈，所以，在跟踪精度上III型ITAE最优伺服系统显著优于现有系统。