内滚道缺陷对滚动轴承刚度特性的影响研究

李雷军 张碧川 高宇翔 韩 沁 陈润霖

（①陕西陕煤曹家滩矿业有限公司，陕西 榆林 719000；②西安理工大学机械与精密仪器工程学院，陕西 西安 710048；③维谛技术(西安)有限公司，陕西 西安 710075）

滚动轴承作为旋转机械的重要连接和支承部件，是整个系统中承受磨损最密集的元件之一[1-3]，其使用性能制约着机械设备的生产效率和使用寿命[4]。在恶劣工况条件下轴承的滚道和滚动体易产生局部缺陷，缺陷经过一段时间的发展形成点蚀失效[5-7]，引起大型设备停机或事故，常常带来很大的经济损失，因此需要分析滚动轴承存在缺陷时的性能，特别是与转子系统安全运行相关的刚度特性。McFadden P D 等[8]建立了缺陷轴承的振动模型，分析了缺陷对轴承振动特性变化规律的影响。Feng N S 等[9]分析了内外圈缺陷对轴承动力学特性的影响规律。Jiang Y N 等[10]分析了滚动体通过不同缺陷时接触力的变化情况。Nakhaeinejad M 等[11]指出缺陷的加深会加剧轴承的冲击响应。涂文兵等[12-13]分析了变速工况下游隙等因素对轴承动态载荷特性的影响，并且分析了缺陷大小不相同时对轴承接触变形和内部接触动态特性的影响规律。陈润霖等[14]建立了轴承存在游隙的刚度模型，分析了不同游隙对轴承刚度的影响规律。Petersen D 等[15-16]建立了考虑外滚道缺陷的时变刚度模型，分析了缺陷对刚度的影响。徐永智等[17]分析了内滚道损伤直径对轴承振动性能的影响规律。王凯等[18]分析了不同工况下复合故障对轴承振动响应的影响规律。文献[19-20]根据缺陷产生的机理，建立了缺陷轴承的动力学模型。

国内外针对带有滚道缺陷的滚动轴承性能研究较多，但是对于时变刚度的研究不多。当存在缺陷时，滚动轴承的刚度时变特性会更加明显，也是轴承转子系统产生振动冲击的机理之一。本文根据赫兹接触理论分析缺陷轴承内部的载荷分布，建立轴承内滚道存在局部缺陷的时变刚度模型，分析内滚道旋转时，缺陷长度和深度对轴承刚度特性的影响规律。相关研究结果和计算数据可用于故障轴承转子系统的动力学计算，并为轴承早期故障的判别提供数据支持。

1 内滚道存在缺陷的滚动轴承刚度模型

1.1 建立内圈滚道缺陷模型

本文针对轴承内滚道存在局部缺陷的情况进行分析，由于滚动轴承内圈与主轴连接并随主轴转动而旋转，因此滚动轴承缺陷位于轴承内滚道时，其位置角随内圈转动呈周期变化。当内滚道存在较小缺陷，即缺陷深度Hb大于缺陷引起的最大附加位移Hmax，滚动体不与内圈缺陷底部接触，为便于对轴承性能进行分析，忽略滚动体的转动惯量，建立如图1 所示的缺陷模型。

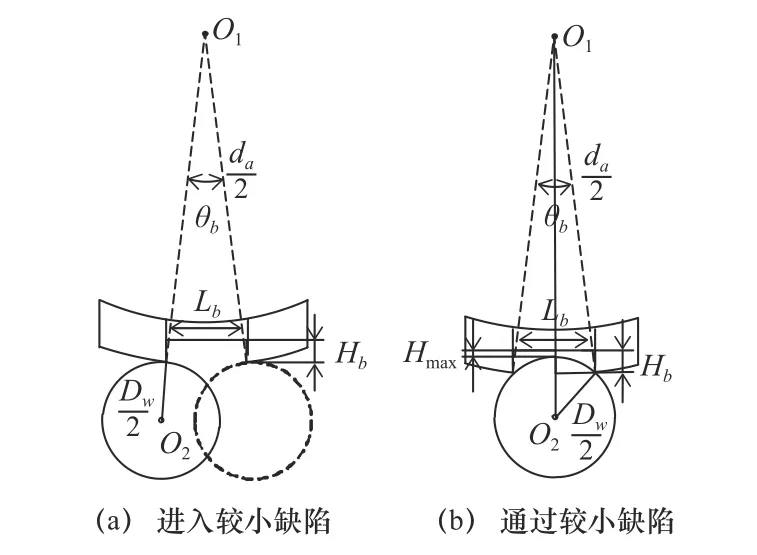
图1 滚动体通过较小缺陷点时的位移分析

当缺陷深度Hb小于缺陷引起的最大附加位移Hmax，或缺陷长度Lb大于滚动体直径Dw，滚动体通过缺陷区时与缺陷的底部接触旋转，附加位移Hf在一段时间内不再改变，均等于最大附加位移Hmax，此时最大附加位移Hmax的大小等于轴承的缺陷深度Hb，滚动体公转进入缺陷区和离开缺陷区，仅与缺陷区域的两端接触。为了简化分析过程，不考虑缺陷表面粗糙度对轴承接触刚度的影响，假设缺陷表面为光滑表面，建立如图2 所示的缺陷模型。

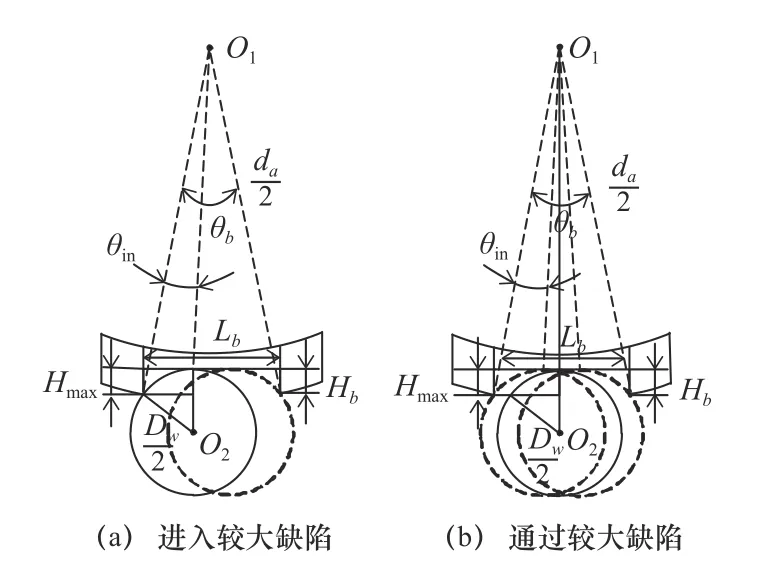
图2 滚动体通过较大缺陷点时的位移分析

图1～2 中，Hf为滚动体进入缺陷区到离开缺陷区期间产生的附加位移，θb为轴承的缺陷角，θin为进入缺陷区到产生最大附加位移点之间的夹角，da为内圈滚道直径，Dw为滚动体直径。

通过较小缺陷时，滚动体与缺陷两端接触的最大附加位移Hmax为：

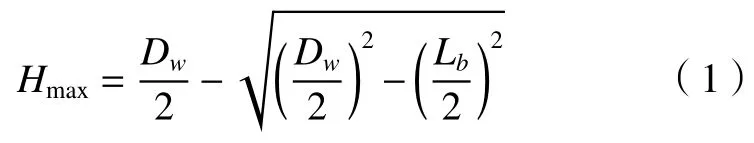
缺陷角θb的大小与缺陷的长度Lb和内圈滚道直径da有关，可根据三角函数关系推导得出：

滚动体公转时进入和离开缺陷区期间产生的附加位移Hf可表示为：

式中：γ是以滚动轴承中心为轴心，滚动体与缺陷起点间的夹角， γ=mod(ψi，2π)-ψb0。

通过较大缺陷时，可由式（2）推导得到轴承内圈的缺陷进入角：

根据式（3）可以得到滚动体公转进入和离开较大缺陷区期间产生的附加位移Hf：

1.2 内滚道存在缺陷的轴承力学分析

建立轴承内滚道存在缺陷的力学模型如图3 所示，图3 中ψb0为轴承缺陷起始点与竖直方向的夹角，即缺陷位置角；θ为滚动体公转角度；ψi为第i个滚动体与轴承轴心在竖直方向上的夹角；ω为轴承内圈的转动角速度；Fr为径向载荷，Fψli和Fψri分别为左右两侧滚动体的法向载荷。

图3 滚道有缺陷的轴承力学模型

当滚动体经过缺陷处且轴承存在游隙Gr时，轴承缺陷处的弹性形变为：

轴承缺陷处的滚动体承载为：

径向载荷作用下，承载区各滚动体所受载荷的竖直分量之和与径向载荷保持平衡：

迭代求解最大滚动体载荷Fmax,当第n次迭代-Fmax≤ε 时，迭代结束。将此时的代入式（9）可得到各滚动体上承载Fψi。

式中：T为载荷分布参数，T=(1-Gr/(2δmax+Gr))/2。

为了更直观地对模型进行求解，绘制如图4 所示流程图。

图4 迭代求解最大滚动体载荷

1.3 刚度模型

缺陷轴承在径向载荷作用下的刚度为：

式中：δψli和δψri分别为左右两侧滚动体的法向弹性变形。

平均刚度的计算参考文献[14]中的公式：

式中：Kt表示滚动体每个公转角度的刚度；n表示滚动体公转角度的数据总数。

2 滚道缺陷对轴承刚度时变的影响

2.1 轴承参数

本文以深沟球轴承6008 为案例轴承，其结构参数如表1 所示。

表1 深沟球轴承6 008 具体参数

案例轴承的最大承载角应满足(-ψmax，ψmax)，可根据式（12）计算：

2.2 内滚道缺陷对刚度的时变特性分析

2.2.1 缺陷长度

径向载荷1 000 N 作用下，当径向游隙为10 μm，轴承缺陷深度为10 μm，缺陷长度分别为2 mm，6 mm，9 mm 时[21]，轴承刚度时变特性的影响规律如图5 所示。从图5 可以看出，当滚动体经过内滚道缺陷区域，轴承刚度减小，且轴承刚度减小的区域随着轴承内滚道缺陷长度的增大逐渐增大。

图5 轴承内滚道缺陷长度对时变刚度的影响

内滚道缺陷长度对轴承平均刚度的影响规律如图6 所示。随着轴承内滚道缺陷长度的不断增大，缺陷轴承的平均刚度整体呈减小趋势。当缺陷位于承载区时，随着轴承内圈的转动，轴承的平均刚度先减小后增大；缺陷位于非承载区时，缺陷对轴承平均刚度无影响。

图6 轴承内滚道缺陷长度对平均刚度的影响

2.2.2 缺陷深度

径向载荷1 000 N 作用下，当径向游隙为10 μm，轴承内滚道缺陷长度为5 mm，缺陷深度分别为5 μm、10 μm和15 μm 时，对轴承刚度时变特性的影响规律如图7 所示。随着轴承内滚道上缺陷深度增大，缺陷处的轴承时变刚度减小幅度逐渐增大。

图7 轴承内滚道缺陷深度对时变刚度的影响

内滚道缺陷深度对轴承平均刚度的影响规律如图8 所示。随着轴承内滚道上缺陷深度的增大，轴承的平均刚度整体呈减小趋势，且平均刚度最小值所对应的缺陷位置角越来越靠近载荷方向的位置。

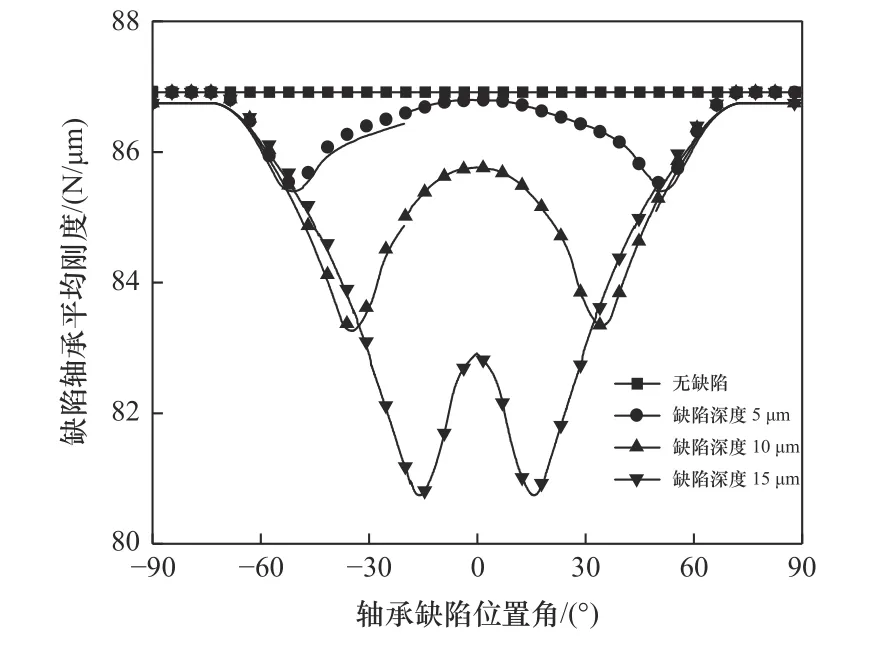
图8 轴承内滚道缺陷深度对平均刚度的影响

3 结语

（1）将内滚道缺陷所产生的附加位移加到缺陷轴承的弹性形变中，并根据力学平衡方程，分析了各滚动体的载荷分布，建立了内滚道存在缺陷的深沟球轴承的时变刚度模型。

（2）分析了内滚道缺陷对轴承刚度的影响规律，当缺陷由承载区向非承载区移动时，缺陷轴承的平均刚度先减小后增大。随着缺陷长度和深度的增大，平均刚度总体逐渐减小，且最小值对应的缺陷位置角逐渐靠近载荷方向。