基于ARIMA和XGBoost的滚动轴承故障预测模型研究*
2022-04-07张天瑞周福强吴宝库朱芷仪宋雨儒
张天瑞 周福强 吴宝库 朱芷仪 宋雨儒
(①沈阳大学机械工程学院,辽宁 沈阳 116300;②沈阳大学机械工程学院国际学院,辽宁 沈阳 116300)
在实际生产中,滚动轴承是大多数机械设备中应用最为广泛的一类零部件,起着不可替代的重要作用。由于滚动轴承长期处在恶劣的工作环境下,使得其成为现代工业中最易受损的元器件之一[1]。比如在滚动轴承的大型发电机的故障中,轴承的故障率达到40%[2]。一旦滚动轴承发生损坏,轻则导致机器等大型设备损坏、影响正常生产,重则造成严重的人员伤亡和财产的损失。为了及时发现滚动轴承故障类型并采取相应对策,要求提前获取轴承振动信号及轴承的数据,一般通过传感器等设备感知其状态;故障诊断和预测就是要分析这些数据从而评估出轴承的工作状态。滚动轴承提取信号的影响因素分为内部和外部两类[3],两类因素的综合作用会对需要提取的振动信号造成影响。因此,针对轴承故障诊断相关方面的研究对于零件、设备和生产过程等各个方面都有重大而深远的意义[4]。
随着故障诊断方面技术的迅速发展,人们对其进行了大量的研究和改进,对于滚动轴承的故障诊断方面的研究逐渐由新兴问题演变为复杂问题[5-6]。
傅里叶变换和小波变换、希尔伯特-黄变换、经验模态分解(empirical mode decomposition,EMD)、补充集合经验模态分解(complete ensemble empirical mode decomposition,CEEMD)和变分模态分解(variational mode decomposition,VMD)等信号处理的传统方法一般从传感器提取的原始信号中提取时域、频域和多域等有效故障特征;传统机器学习的方法在故障诊断方面也得到明显的应用并发挥其优势[7-9];上述方法仅仅在一定程度上、单方面地满足轴承故障对其准确度等的要求。马怀祥[10-11]等从模型分类方面,提出卷积神经网络(CNN)和极端梯度提升(XGBoost)的滚动轴承故障诊断方法,用以提升模型预测准确度。Hu X 等[12-14]为了提高频谱精度,提出了基于LMD和频谱校正的滚动轴承故障诊断方法。而龚立雄[15-16]等从特征提取方面入手,提出基于核函数主元分析的轴承故障分类方法,非线性分类对准确度提升有很大帮助。本文结合了前人多篇关于滚动轴承故障诊断方面的文献,在工业大数据和深度学习的背景下,提出一种基于局部均值分解(local mean decomposition,LMD)和固定点算法(fixed points algorithm,FPA)联合降噪、核主成分分析(kernal pricipal component,KPCA)和极端提升决策树算法(extreme gradient boosting,XGBoost)思想结合自回归积分滑动平均(autoregressive integrated moving average model,ARIMA)时间序列模型的轴承故障诊断方法。基于滚动轴承故障诊断降噪-提取特征-分类(故障识别)所使用的不同方法,本文构建了滚动轴承的故障诊断模型,并使用美国凯斯西储大学轴承数据集进行仿真验证。
1 故障诊断过程
滚动轴承诊断和预测的事先准备过程为信号降噪和敏感特征提取:由于滚动轴承的工作环境复杂等影响条件下,提取的轴承信号具有大量背景噪声,而其存在影响敏感特诊提取,进而影响故障识别的准确度;用于轴承状态检测的特征指标有很多种,一般分为两类,基于时域特征(是否存在故障)或基于频域特征(故障内在原因)的选取。同传统的轴承故障诊断的特征选取环节中不同的是,本文不采用单一的基于时域、频域的输入指标,而是通过多域提取出的特征(全面表现轴承的状态变化过程)作为诊断模型的输入,选取敏感多特征指标进行诊断分类,即为滚动轴承故障识别的过程。现多使用改进神经网络、隐马尔科夫模型和支持向量机等轴承故障诊断方法[17-18]。但由于面临生产环境爆炸式增长的数据量的现状,传统的机器学习算法计算的准确度上相较于深度学习略显不足。近年来,大数据方面应用较广的 XGBoost算法能够有效地应对上述问题;预测未来短时期滚动轴承信号趋势的方法一般有支持向量机(support vector machine,SVM)、灰色理论和ARIMA 等;ARIMA 自回归模型具有计算效率、准确度高[9]等特点,因此本文采用ARIMA进行故障预测。图1 中阐述了故障识别和预测的一般过程:首先需要通过适合的传感器采集到轴承的振动信号,振动信号经过滤波处理之后再经由敏感特征选取结合历史数据使用ARIMA 自回归模型预测未来的振动趋势,再将预测的结果输入到XGBoost数学模型中进行验证,最后根据预测的结果做出相应的对策。
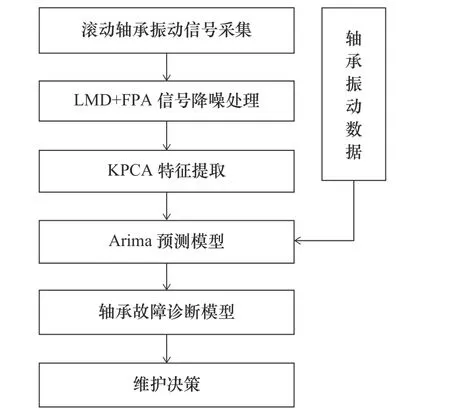
图1 滚动轴承信号预测和故障诊断过程
2 理论和求解过程
2.1 LMD+FPA 联合降噪
由于滚动轴承受到工作环境等影响,其通过传感器获取的滚动轴承的原始信号中包含大量无用噪声干扰,降噪后的原始信号又需要进行提取特征的环节,而特征提取的参数又作为诊断模型的输入;如果包含的噪声不能有效去除,其提取的特征会与真实值发生明显的差异,进而影响诊断模型的准确度。因此,对于原始信号的降噪处理显得尤为重要。
LMD 是一种基于时域和频域的自适应信号分析方法;其本质在于将原始信号分解为若干个分量值和残余值。为了克服传感器接收到的原始信号中具有不同信号源产生的多种信号的混合信号,又采用独立分量分析(independent component analysis,ICA)[13]方法解决上述问题。ICA 方法又被称为固定点算法FPA。固定点算法基于不同信号源头之间统计的相互独立性,它同传统的滤波方法相比,对要求的原始信号的细节保留得更为彻底。综上,本文采用LMD+FPA 联合降噪的方法。下面是LMD 降噪方法在处理原始信号时的推导过程:
(1)选取包含大量噪声的原始信号s(t),寻找其不间断的极小值mk,c和极大值mk,c+1,顺序计算两两邻近的极值间的局部均值ni,k。极值点的相序数以c来代表;k代表求解极值过程的总次数;i代表有多少个分解完成的PF分量。再按照顺序求解相邻的极值差得到局部包络值:局部包络值和平均值的计算公式为:
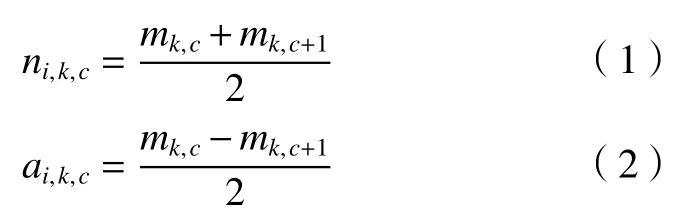
(2)局部包络函数ai,k(t)以 及局部均值函数ni,k(t)即为两值之间构成的连续函数,通过移动平均(MA)法对上述两个函数进行平滑处理。
(3)去除局部均值函数以后得到hi,k(t),再通过ai,k(t)进行解调得到调频函数zi,k(t):
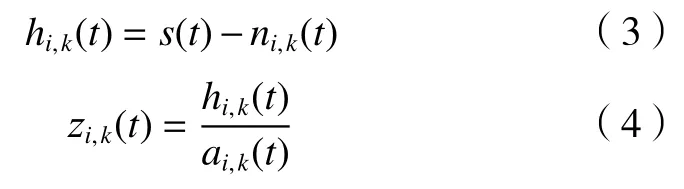
(4)局部包络函数ai,k(t)越接近1,调频函数zi,k(t)越 能满足纯调频信号的条件。一般地,1-δ≤ai,k(t)≤1+δ的条件用来判断局部包络函数ai,k(t)能否满足纯调频信号。δ是预先确定好的一个较小参数。当条件满足时计算乘积函数;若条件不满足,则令ai,k(t)乘ai,k-1(t)后返回第一步。当条件满足时得到纯调频信号zi,k(t), 纯调频函数zi,k(t)在 [-1,1]范围内的包络信号ai,k(t)=1。当ai,k(t)与接近1时,将局部包络函数ai,k(t)相乘,ai(t)为 包络信号,q为最终的循环次数:
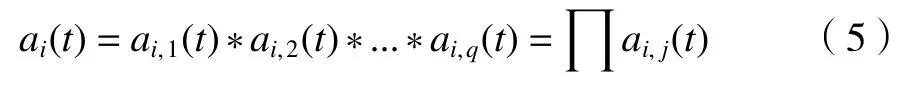
(5)将ai(t)与zi,q(t)相乘,可以得到乘积函数PFi(t),zi,q(t)为纯调频信号;用乘积函数PFi(t)减去原始信号s(t)得到剩余信号。剩余信号ui(t)则重复(1)~(5)的过程,一直到满足条件之后剩余一个单调函数或极值点未知,停止计算。
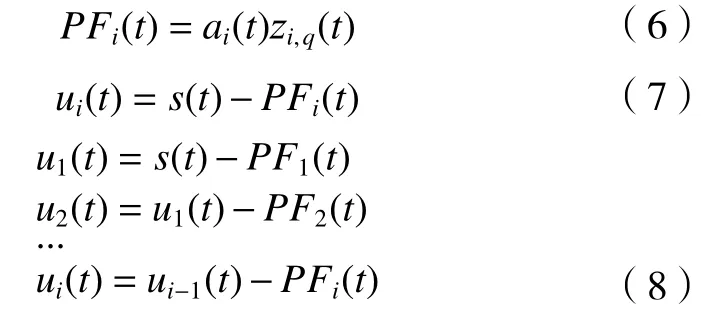
经过上述几个步骤之后,复杂原始信号s(t)在经过上述迭代过程以后被分解成n个乘积函数PF和一个剩余函数un(t):
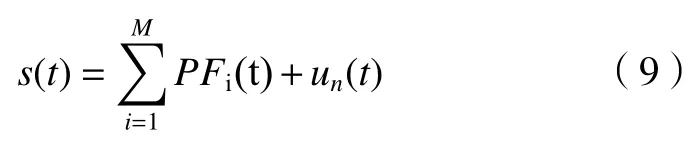
LMD 过程中各个变量的含义:s(t)为原始信号;mk,c为局部极小值;mk,c+1为 局部极大值;ni,k为局部均值;c为极值点序数;k为求解极值次数;i为PF分量个数;ai,k(t)为局部包络函数;ni,k(t)为 局 部 均值函数;zi,k(t)为 调频函数;ai(t)为 包络信号;q为循环次数;PFi(t)为乘积函数;zi,q(t)为纯调频信号;ui(t)为剩余信号。
由于FPA 只适用于观测信号的数量大于等于源信号数量的情况,要求LMD 方法能够来解决ICA方法下的欠定盲源分离问题。本文使用LMD 降噪方法将原始信号剔除剩余信号(噪声值)后,又将重构虚拟的观测信号和观测信号构成一个新的二维矩阵,矩阵作为ICA的输入。首先,LMD 方法将原始信号分解为若干个PF 分量。其次选取相关程度较大的分量信号之间重构形成虚拟观测信号。最后重构得到的虚拟观测信号和原始混合信号之间组成一个新的二维矩阵,使用ICA 方法予以分析分解,最终达到对原始信号中滤除无用信息的目的。两种方法联合降噪过程如图2 所示。
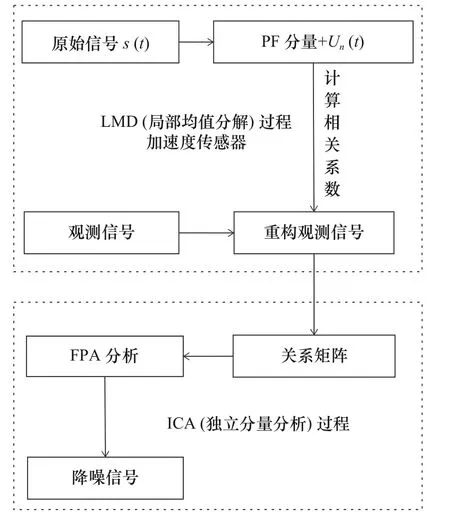
图2 LMD+FPA 联合降噪过程
2.2 KPCA 特征提取过程
核主成分分析KPCA 又被命名为核主分量分析。和PCA 方法有所区别的是,KPCA 采用非线性方式进行样本的空间变换,通过选取合适的非线性函数将原始的样本数集映射到高维空间中,再在高维空间上对样本的多向量进行主成分分析。因为其具有包含非线性分类方式的特点,非线性数据集的问题通过KPCA来解决是十分合适的[16]。
核主成分分析通过非线性方式把低维空间的数据向量转换到另外一个高维空间F,再计算协方差矩阵C。协方差矩阵C的特征向量和特征值需要满足以下条件:
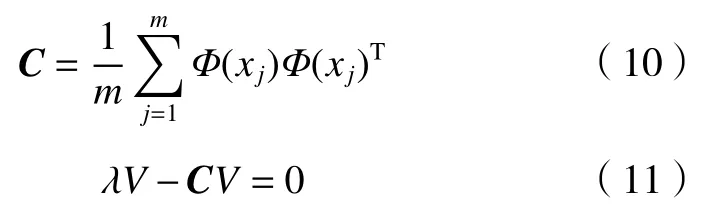
Φ(xj)为非线性函数,将其代入后得到:
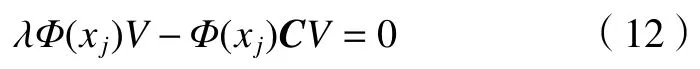
特征向量可以用 Φ(xi)来线性描述,即:

引入核函数Kij=K(xi,xj)=Φ(xi)Φ(xj),简化后可以得到:

综上,随机选取的样本在特征空间F中主元成分 Φ(x)上的投影可以表示为:
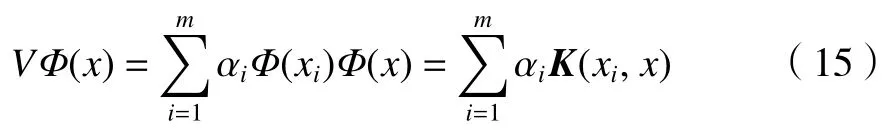
KPCA 过程中各个变量的含义:F为高维特征空间;m为低维空间样本数量;xi为低维空间样本;Φ(xj)为 非线性函数; Φ(xi)为高维空间样本点;K为核矩阵;C为协方差矩阵;V为C的特征向量;λ为C的特征值;α为K的特征向量。
2.3 Arima 预测振动信号
Arima 模型的基本原理是借助自身原始的数据集合经过差分处理之后再通过自身数据的特点进行未来一段时间内数据的预测[9]。相关图用来判断使用MA、AR 或者AR-MA 模型,若时间序列通过N阶差处理后达到平稳状态,则使用Arima 模型。下式为Arima 模型的计算公式:
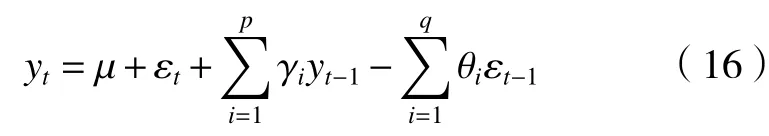
式中:µ代表常数项;εt为随机误差值;γi为自相关系数;θi为 移动平均系数;p为自回归项、q为移动平均项、d为时间序列平稳所需的次数。预测的数据集若为非平稳序列,一般先通过差分处理转化为平稳序列,再使用AR-MA 模型进行拟合;若为平稳非白噪声序列,需要求出自相关系数和偏相关系数结合相关图分析得到p、q值。
2.4 XGBoost 过程
XGBoost 是华盛顿大学的陈天奇博士在2016 年基于梯度提升决策树算法提出的一种基于梯度提升决策提升集成学习算法[12]。它经由GBDT 算法改进后得到,它的学习器可以是CART 决策树(GBTree),也可以是线性分类器(GBLinear)。一般来说,XGBoost、GBDT 算法和随机森林是一个递进的关系。其中,GBDT 算法在随机森林的基础上融合了XGBoost 思想,使得森林的树之间建立联系而不是独自存在,形成一种整体有序的决策测体系。同样地,XGBoost算法以决策树作为基础,引入了二阶泰勒展开和正则项,可以有效地控制模型的复杂程度(模型方差大幅度降低),训练后的模型更简单和稳定。XGBoost 能够为运算过程中产生的缺失值设定分支的默认方向,此外XGBoost 还支持特征级别上的并行计算,加入的正则项防止过拟合和欠拟合现象的产生。XGBoost的关键是建立多个决策树来有效地降低预测结果的误差,并保证回归树组成的树群有尽量大的泛化能力[19-20],最优泛化函数(Loss)的表达式如下:
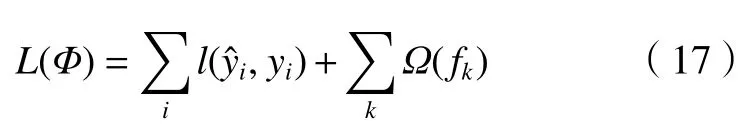
式中:求和函数分别为误差函数和正则惩罚项。误差函数中的参数yˆi是整个模型的输出;正则惩罚项表达式如下:
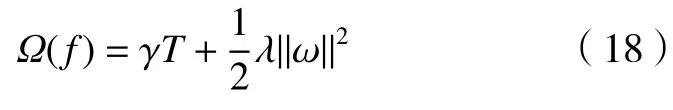
式中:T为决策树叶子节点个数;ω为节点;XGBoost中要求对Loss 函数进行二阶泰勒展开:

3 数值验证和仿真过程
3.1 数值验证
本文采用的轴承数据集来自美国凯斯西储大学。使用的Python 版本为3.8.5、电脑CPU 为i7-9750h;使用的内存大小为16 GB。本次使用的滚动轴承数据集中包含7 个样本:选取5 组作为训练集,剩余2 组作为测试集。
3.2 数据分析
滚动轴承的整个运行周期是从完全健康状态开始一直到发生不同类型的损坏以后结束的。传感器为了全面监测轴承整个周期的状态变化,从完好的状态开始进行记录,直到发生故障以后停止记录。因此采集到的滚动轴承的信号包含有用的信息。本文选取前5 个样本数据使用LMD+FPA 降噪完成预处理后进行特征提取。本文综合考虑了时域特征和频域特征,对经过降噪的原始信号进行KPCA 方法处理来得到多域特征,包括滚动体故障的特征和内圈故障等敏感特征,提取后的敏感特征作为诊断模型的输入。
3.3 Arima 模型预测
Arima 模型用来预测未来一段时间内信号发生的变化,用以判断数据是否稳定,并选取差分次数为1;时序图围绕其均值上下波动,自相关图短期相关性较强。图3和图4 分别为原始信号和原始信号经过1-2 阶差分处理之后得到的结果,图5 为Arima 模型的振动信号预测结果。
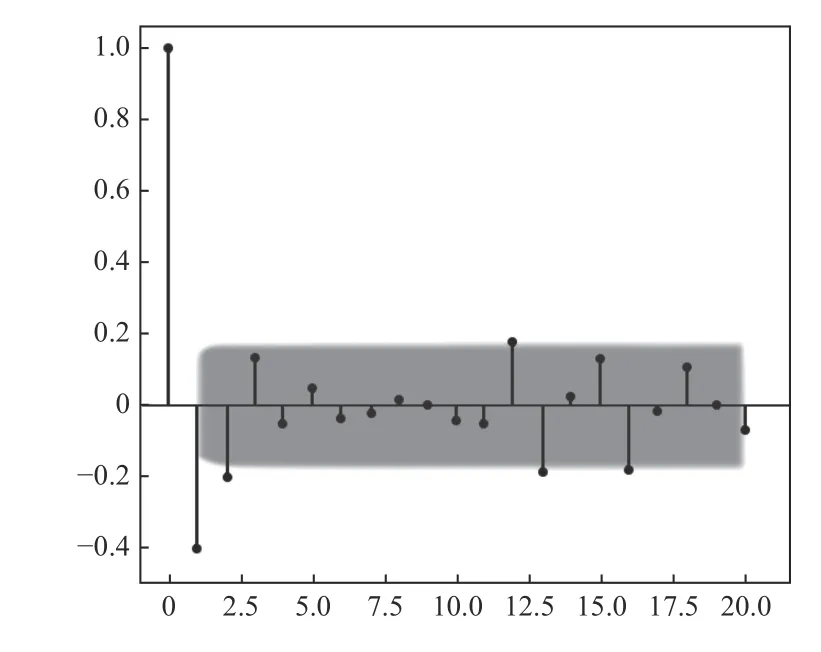
图3 1 阶差分(ACF)
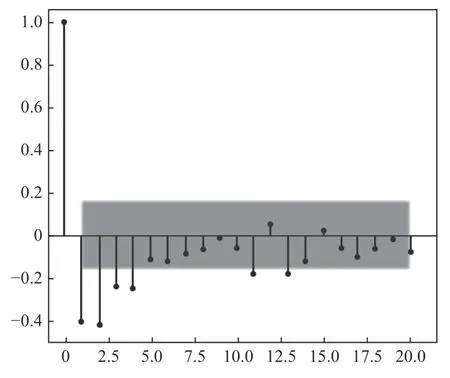
图4 2 阶差分(PACF)
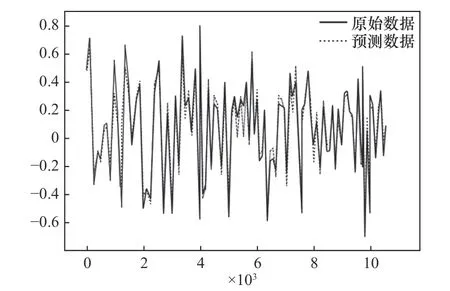
图5 Arima 预测振动信号图
经过差分处理之后的数据用Arima 模型加以预测:选取11 000 个数据进行预测,预测完未来时期内的振动信号之后,还需要对其进行指标评估。常用评估指标如表1 所示[20]。
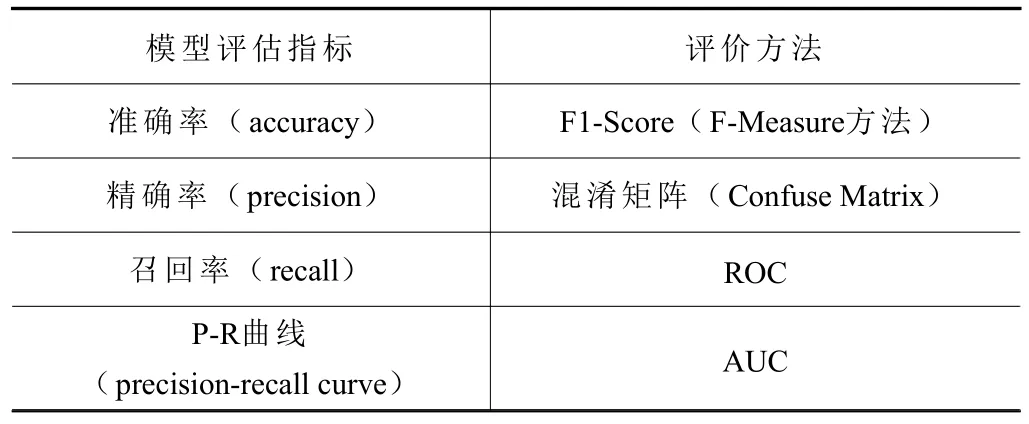
表1 几种常见的模型评估标准
由于单一评估指标只能片面反映模型的性能,因此需要综合地使用多个评估指标才能准确反映模型的预测结果。本文采用了准确率、精确率、召回率3 个方面作为模型的评估标准。评估结果如表2所示。
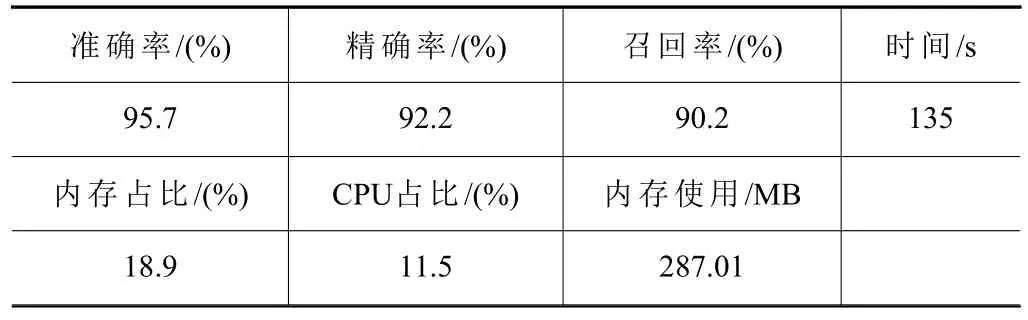
表2 ARIMA 预测振动信号性能
3.4 XGBoost 分类
XGBoost 将提取好的特征作为分类模型的输入,为了方便区分,本文将轴承的几种状态用不同的数字加以表示:1 代表滚动体故障,2 代表外圈故障,3 代表内圈故障;0 为无异常状态。0~3的作为分类模型的输出。本次实验使用前5 组作为训练数据,经过降噪和提特征后输入分类模型中进行训练。XGBoost 模型的各个参数为:最大树度为22;学习率选取为0.35;最小权重为0.1,而Score 得分为0.953。使用最后两组数据用于测试,预测结果如图6、7 所示。
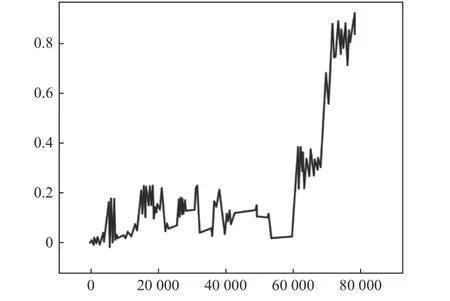
图6 第一组测试集的预测结果
图6 中:10 000~40 000 虽然样本数据期间发生波动,但波动程度较小,直到40 000~60 000 数据又趋向于平稳状态。当接近60 000 组数据时,发生明显波动,且60 000~70 000 值上升较快,代表轴承发生故障状态的可能性增高,值围绕在0.8 附近,根据之间分类的结果判定为滚动体故障,与实际结果相符合;图7 中0~5 000 组波动较小,5 000~10 000样本间基本上趋于平稳,13 000~20 000 组时波动情况较大,20 000 组以后值明显升高,根据模型输出结果判别为内圈故障,与实际结果一致。两组测试结果均反映此模型可以较好地反映轴承故障的类型。
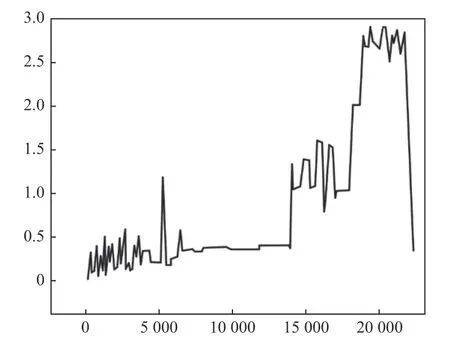
图7 第二组测试集的预测结果
4 结语
本文针对滚动轴承故障诊断问题中的背景噪声大,提取有效特征难和传统机器学习算法准确度低的问题上,提出了基于Arima 自回归和XGBoost 思想的模型用于轴承故障诊断和预测的方法。经由美国凯斯西储大学轴承实验数据进行实例验证证明了本方法可以短时期内预测轴承状态和故障类型,以便于为滚动轴承的后期维护、更换等做好准备。
(1)Arima 自回归模型在处理非平稳振动信号采用N阶差分的方式,可以短时间内预测轴承信号的走向和趋势。
(2)XGBoost 算法在应对残差值的处理方面优于GBDT 集成思想算法的改进,能够有效地纠正诊断过程中发生的误差,不断进行修正,提升了模型分类和预测的准确度。
(3)基于Arima+XGBoost的滚动轴承故障识别和预测方法不仅在数值仿真过程中得到有效应用,也为滚动轴承应用于各种大型机械设备在实际生产中提供了一种参考方案。
