基于时隙ALOHA与NOMA的通信系统性能分析

杨梦珂,翟道森,费聚锋,张若南,杨炎坤,张 伟

（1.西北工业大学电子信息学院,陕西 西安 710072;2.上海无线电设备研究所,上海 201109）

0 引言

时隙ALOHA协议是纯ALOHA协议的改进。该协议通过将媒介接入的时间划分为较小的时隙来提高吞吐率,并通过有效降低发送数据包的随机性,减小数据碰撞概率,从而提升通过率,改善通信系统性能。时隙ALOHA协议相关性能分析已较为完善。非正交多址接入（nonorthogonal multiple access,NOMA）是5G通信时代的重要技术,该技术可以实现有限频谱资源的复用,解决部分数据包的碰撞问题,从而获得更低的丢包率和更高的传输速率。

目前,已有十多种非正交多址接入方案,研究较多的是功率域非正交多址接入（power-domain non-orthogonal multiple access,PD-NOMA）技术。此外,各大通信公司还对基于码域的多路复用技术开展了深入研究。针对5 G标准,各大公司已经形成了一致的意见,NOMA至少要连接一百万终端/平方公里的上行海量机器类通信（massive machine type of communication,m MTC）场景,而对于其他场景是否需要使用,待进一步研究与评估。

本文讨论时隙ALOHA和NOMA结合的新系统的工作模式,对其性能做理论分析与仿真,分析新系统相对时隙ALOHA系统的性能差异及原因,并对比两种系统冲突分解时的通过率差异。

1 新系统理论性能分析与仿真

1.1 理论性能分析

在时隙ALOHA协议中,时间轴被划分为若干个与数据包传输时间一致的时隙,只有在时隙的开始时刻才能发送数据包,即数据包在某时刻到达后,将在下一个时隙的开始时刻进行传输。若同一时隙内仅有一个数据包到达,则成功传输;若某时隙有两个或两个以上数据包达到,则发生碰撞。

而在功率域NOMA协议中,系统在发送端选择不同的发送功率,在接收端进行连续干扰消除,可以在相同时频资源条件下通过不同的功率等级实现多址接入,成功传输数据包,从而提高系统的通过率。

现讨论时隙ALOHA与NOMA结合的系统。该系统有c个发送节点,每个节点的到达过程是参数为μ/c的独立泊松分布过程,其中μ为系统新到达数据包的的到达率。时隙的长度与数据包传输时间一致,只有在每个时隙的开始时刻才能传输数据包。功率域上为系统提供L个功率等级,不同功率等级的数据包能同时被成功传输。时隙ALOHA与NOMA结合的新系统工作原理如图1所示。

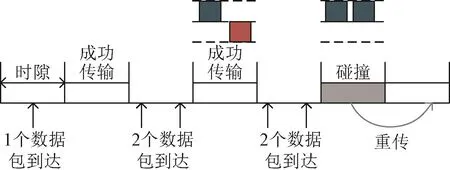
图1 时隙ALOHA与NOMA结合的新系统工作原理图

一个数据包在某时刻到达,若该时刻对应时隙内仅有一个数据包到达（包括新到达和重传到达）,则该数据包可以在下一时隙成功传输;若在此时隙内有多个数据包到达,则要判断这几个数据包是否能够通过不同功率等级被区分,从而成功传输。显然一个时隙内最多有L个不同功率等级的数据包被成功传输。若多个数据包占用了相同的功率等级,则会发生碰撞,碰撞的分组将在之后的时隙中进行重传。设碰撞后重传的时延足够随机化,则新到达数据包和重传数据包的到达过程,可以近似被认为满足到达率G＞μ的泊松分布。根据泊松公式,单位时间内产生k个数据包的概率

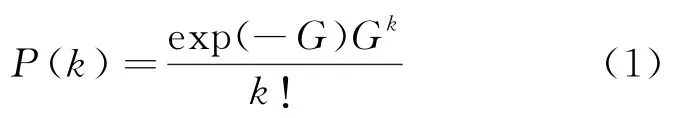
根据上述分析可知,系统成功传输的概率P分为两部分,一部分是一个时隙内仅有一个数据包到达的概率P,另一部分是有多个数据包到达但可通过功率等级区分的概率P,即

其中,P与时隙ALOHA成功传输的概率一致,可表示为

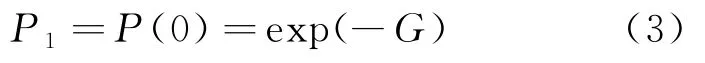
设k为一个时隙内到达数据包的个数,每个数据包落在某个功率域上的概率均为1/L,用P表示功率域有L个等级时,时隙内有k个数据包到达且能成功区分的概率,则有

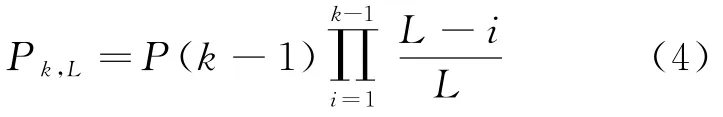
多个数据包到达时,可通过功率等级区分的概率P可表示为

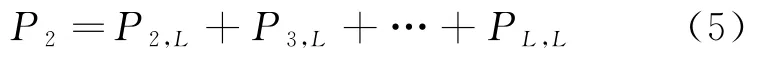
整合式（4）和式（5）,得

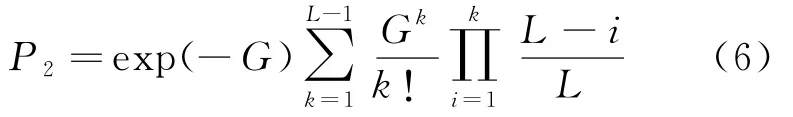
则系统成功传输的概率P可表示为

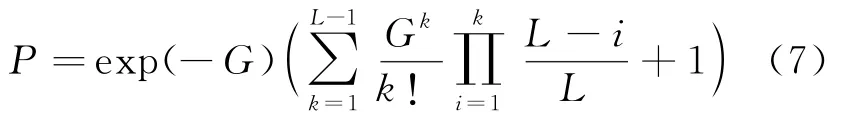
因此,时隙ALOHA与NOMA结合系统的理论通过率

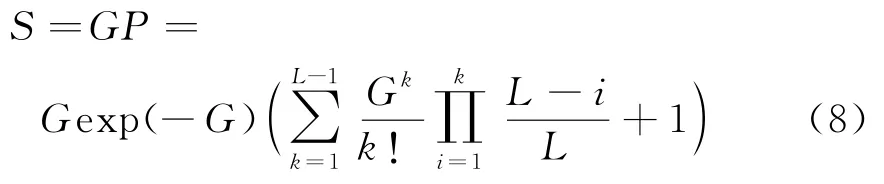
对式（8）求最大值,可得到系统的最大理论通过率和对应的最佳到达率。

1.2 仿真分析

仿真的设计思路是在给定时间内为数据包随机分配到达时刻和功率等级,通过对应时隙与功率判断其是否发生碰撞,统计成功传输的数据包数目,从而计算系统的通过率,最后将仿真结果与理论分析结果进行比对。

用变量m表示观察时间内发送数据包的数目,改变m的取值可以改变到达率G的分布范围;每个数据包的宽度,即时隙长度,记为T,取值为0.001;定义m×1维随机矩阵A和P,其元素的取值在0～1范围内平均分布;将矩阵A和P根据时隙数目和功率等级数目扩大相应的倍数并向上取整,分别用以代表数据包达到传输所占的时隙标签数A和所处的功率等级P;将矩阵A和P转化为向量并记为矩阵C和H。设置完仿真环境后统计成功传输的数据包数目N并存储。数据包是否成功传输的判断方式为:

a）若C中的某个值仅出现了一次,则此时隙仅发送了一个数据包,N=N+1;

b）若C中某个值出现了两次,且这两个数据包对应的功率等级不同,则此时隙成功发送了两个数据包,N=N+2;

c）以此类推,直到出现次数与功率等级数相等。

统计结束后计算到达率G与通过率S。到达率G是单位时隙内到达数据包的数目,可用观察时间内发送数据包的数目m与时隙长度T的乘积mT表示;通过率S是指单位时隙内成功传输的数据包数目,可用成功传输的数据包数目N与时隙数目（设为1 000）的商N/1 000表示。重复上述过程50次并求结果的均值,系统的理论通过率的仿真结果如图2所示。

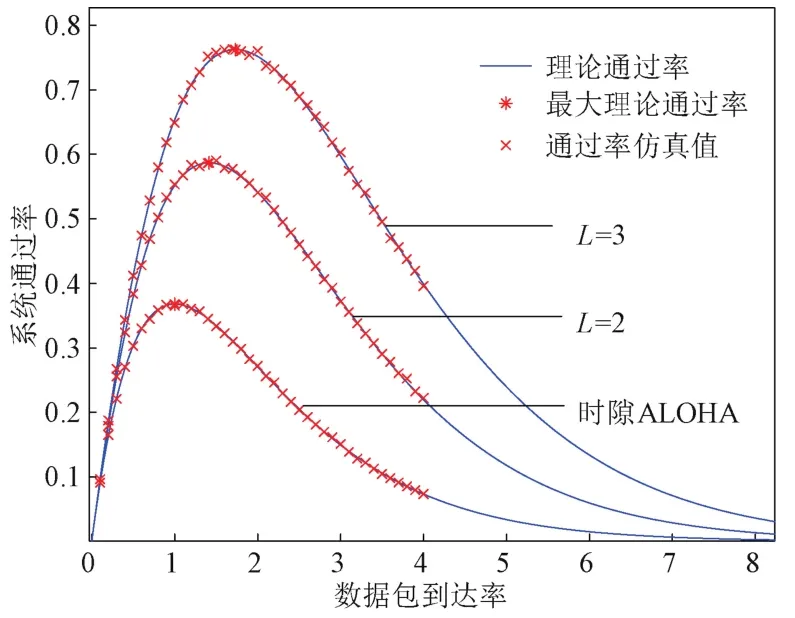
图2 系统的理论通过率仿真结果

由图2可知,时隙ALOHA与NOMA结合系统的通过率随到达率的变化趋势与时隙ALOHA系统相似,均为先增后减。到达率从0开始增加,随着到达数据包数目的增加,成功传输的数据包数目也会增加。但当到达率增至一定数值时,一个时隙内可能到达多个数据包,数据包发生碰撞、传输失败的概率大大增加,成功传输的数据包数目反而减小,这就导致曲线趋势先升后降。

功率等级数目增加后,同一时隙内有多个分组到达,因功率等级不同,数据包被成功传输的概率增加,因此系统通过率增加。功率等级数目增加后,系统达到最大通过率所对应的到达率也会增加。功率等级数目越多,时隙内有更多数据包到达时,能成功传输的概率也越大,因此系统达到最大通过率时对应的到达率也越大。

2 最大通过率及最佳到达率求解

在1.1节中已求得系统通过率的理论表达,现根据式（8）,对系统的最大通过率和最佳到达率进行求解。

当L=1时,系统为时隙ALOHA系统,通过率为Gexp（-G）,用数值分析法简单求导可得,当G=1时,系统获得最大通过率S≈0.368。

当L≥2时,系统为时隙ALOHA与NOMA结合的系统,通过率理论公式较为复杂,不能采用数值分析方法,求解最大通过率和相对应的最佳到达率。此时可通过算法,如黄金分割法,求解最佳性能。求解思路如表1所示。

表1 黄金分割法求解最佳性能

经过求解,当功率等级数目L为2时,系统的最大通过率为0.59,对应的最佳到达率为1.414;当功率等级数目L为3时,系统的最大通过率为0.76,对应的最佳到达率为1.732。

3 冲突分解

已知对于一个时隙ALOHA系统,当两个数据包在第i个时隙发生碰撞时,若每个数据包以1/2的概率独立在第i+1和i+2个时隙上重传,此时的冲突分解通过率为2/3。下面对时隙ALOHA与NOMA结合系统的冲突分解通过率做性能分析。

假设一个功率等级数目L为2的时隙ALOHA与NOMA结合的系统,有两个数据包在第i个时隙发生碰撞,每个数据包以1/2的概率在第i+1和i+2个时隙内独立重传,且以1/2的概率在两个功率等级上独立重传,讨论这种冲突分解方式的通过率。

若两个数据包在第i+1个时隙内成功传输,则意味着两个数据包分布在不同的功率等级上,此时仅需一个时隙就可以解决碰撞。若两个数据包在第i+2个时隙上成功传输,则存在三种可能:第一种是在第i+1个时隙再次碰撞后,两个数据包在第i+2个时隙上同时重传且位于不同的功率等级;第二种是数据包在第i个时隙上发生碰撞后,分别在第i+1和第i+2个时隙上进行重传,则不需要判断功率,直接成功传输;第三种是在第i个时隙发生碰撞后,两个数据包在第i+2个时隙重传且位于不同的功率等级。此时需要两个时隙解决碰撞。以此类推,第i+k个时隙解决碰撞的概率P如表2所示。

表2 第i+k个时隙解决碰撞的概率

两个数据包成功传输所需的平均时隙数

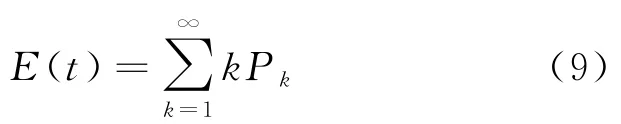
由于每两个数据包需要k个时隙才能传输成功,经计算平均需要1.33个时隙才能成功发送两个数据包。因此上述时隙ALOHA与NOMA结合系统的冲突分解通过率为1.50,大于时隙ALOHA系统的冲突分解通过率。

4 结论

经过理论分析和仿真实验,时隙ALOHA与NOMA结合系统的通过率和冲突分解的性能均优于时隙ALOHA系统,有进一步研究与应用的价值。但本文所讨论的系统是理想状态下的,默认环境是每一个接收节点与发送节点之间的距离相等或相近,因此环境因素对不同节点的影响可忽略不计。在实际应用中,还需要考虑如何为数据包分配功率等级、消除环境因素对不同节点的干扰等问题,同时,该系统的算法复杂度会比时隙ALOHA系统更大。