基于道路网络的LED 路灯聚类组网算法的研究*

孙同陈 李 峰

（江苏大学计算机科学与通信工程学院 镇江 212013）

1 引言

汇聚节点在ZigBee 无线传感网络中起着重要作用，是无线传感网络的集群中心。选择合适的位置部署汇聚节点不仅可以提高底层mesh 无线组网的可靠性，同时也提高了无线传输速度［1］。由于汇聚节点部署在集中控制器内部，对于汇聚节点的选址实际上也是对集中控制器选址。

目前，国内外对于路灯集中控制器的选址研究较少，现有的选址方案主要分为三种：基于能耗的选址方式［2］，基于寿命的选址方式［3］，基于移动汇聚选址的方式［4］。大都是围绕如何降低能耗实现各传感节点能耗均衡出发，在实际项目中，路灯汇聚节点部署在集中控制器内部，由集中控制器供电，不需要考虑节点能耗的问题。文献［5］中，提出了一种基于综合度量聚类的方法实现子网划分。该方法综合考虑了环境对路灯底层子网划分的影响，结合k-mediods 算法进行聚类分析，对汇聚节点的选择有一定参考依据，但是k-mediods 算法适用于球状簇数据，道路网络情况复杂，缺乏对路灯数据基于道路分布约束的考虑。

文献［6］中，针对基于道路网络分布的数据对象提出eb-cls算法，该算法本质上是一种层次聚类算法，适用于任意形状簇的数据，提高了层次聚类算法的运行效率，然而，在ZigBee无线传感网络中，单个汇聚节点的内存是有限的，即它所能接收到的其他传感节点数量是有限的，同时，节点间的Zig-Bee无线传感距离是受环境影响的。

本文在文献［6］基础上提出了基于道路网络的路灯聚类组网算法SLCNARN，在道路网络环境中，增加了聚类算法对基于环境的网络距离定义、路灯集中控制器容量以及对路灯基于道路分布特点的考虑，并利用对比实验验证该算法的可行性。

2 基本模型和定义

本文首先引入路网模型、网络距离等定义［8~9］，将道路网络表示为图，将道路路段映射为图的边，将路段的交叉节点映射为图的结点，将路灯节点映射为对象。路网模型和网络距离的引入，极大简化了路灯数据的复杂程度，同时也较好地反映了路灯数据基于道路网络分布的特点。然而，在路灯节点间（ZigBee）通信的过程中，路灯节点的通信距离有限，同时还会受到环境因素的制约，此外，作为需要存放路灯节点信息的集中控制器容量也有限。

因此，针对不同环境下路灯节点间通信距离不同的特点，增加了对基于环境影响的网络距离的定义；然后结合集合集中控制器容量有限的特点，对路灯聚类的约束条件进行定义。

定义1：道路网络与路灯节点。

道路网络可以表示为无向图G={V，E，W}，其中，V 是路段交叉结点的集合{v1，v2，…，vn} ，E是各个路段的集合{e1，e2，…，en}，W是路段长度集合，表示边对应的权值。路灯节点位于图的边e上，可以表示为一个三元组(vi，vj，p)，其中，vi和vj为路灯节点所在边的两个结点，p为路灯节点到它所在网络边结点vi的距离，取值范围为[0，W(e)]。

对象间的相似性通常用欧式距离来度量，距离越近相似性越高，基于路灯节点之间通信连接的特性，采用网络距离来取代欧式距离。

定义2：路灯节点间的网络距离。

1）因为道路网络模型的边是基于道路路段的交叉结点划分，所以同一路段上面的两个路灯x，y之间的网路距离采用直接距离D(x，y)，定义为

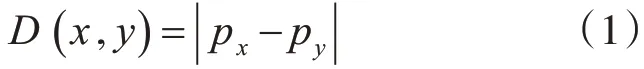
其中，px和py分别表示为在同一条网络边上的对象到结点的距离。

2）同一路段上路灯节点到所在边上结点间的网络距离。

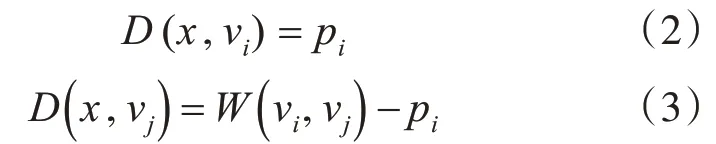
其中，D(x，vi)表示路灯节点x到所在结点vi的距离，D(x，vj)表示路灯节点x到所在结点vj的距离，W(vi，vj)表示结点vi和结点vj之间的距离。

路段结点间的网络距离D(vi，vj)。即网络节点间的最短路径距离，采用迪杰斯特拉算法求解。

3）不同路段上的路灯节点之间的网络距离，定义为

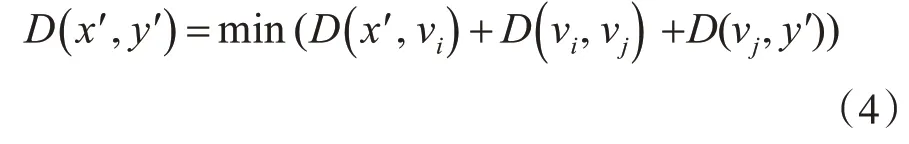
其中，D(x′，vi)表示路灯节点x′到所在结点vi的距离，D(vi，vj)表示不同路段结点间的最短距离，D(vj，y′)表示路灯节点y′到所在结点vj的距离。

定义3：聚类间的网络距离。为两个聚类边界上面的路灯之间的最短网络距离。假设聚类Cm={pm1，pm2，…，pmz}，Cn={pn1，pn2，…，pnz}，则聚类间的网络距离定义为

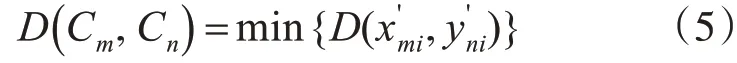
定义4：基于环境影响的网络距离。

由于在实际的项目部署过程中，路灯终端节点间的有效通信距离会受到节点附近的环境影响，比如，树木建筑物的遮挡。在此，通过引入环境综合影响因子来表征环境对路灯节点的影响程度，同时考虑到ZigBee节点，则网络距离，在此定义为

式中，γx和γy分别表示路灯节点对应的环境综合影响因子。其中，γ的取值可以参考室外无线信号路径损耗模型［10~11］定义如下：

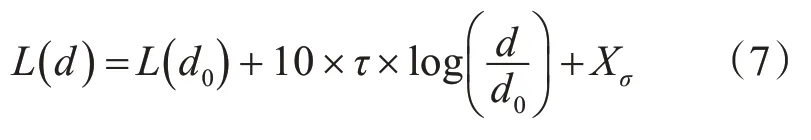
路灯节点既可以作为发送节点也可以作为接收节点。式中，d 是到发送节点的距离，L（d）是距离发送节点d处的路径损耗；d0为参考距离，一般取值为1m，L(d0)为距离发射节点距离为d0的路径损耗；τ为路径损耗指数，表示路径损耗随距离增长的速率，它与传播环境有关；Xσ为阴影衰落引起的样本标准差，为零均值的高斯分布。

信道链路损耗的影响因素较多，与所处的环境、工作频段等有关，在这上面，国内外有很多学者进行了大批量的测试，并对相关参数进行了统计分析，根据Sohrabi K［12］等在各种不同的传播条件下，针对固定频率范围内的测试结果可知，树木的浓密程度对无线信号的强度有较大影响。在城市道路建设的过程中，道路两旁的绿化设施会导致路灯信号传播过程的衰减，在SLCNARN算法中，综合考虑通讯模块信号、路灯间距和绿化程度等因素，对信号衰减区域进行简单的划分，对γ进行不同的取值，如表1所示。

表1 综合环境影响因子分类

定义5：路灯聚类块。

当Cl 满足下列条件时，称非空集合Cl 为一个路灯聚类块。

1）路灯节点总数≤集中控制器容量θ。

2）相邻两个路灯节点间的距离≤最大有效通信距离ε。

其中，集中控制器的最大负荷θ，是出于对集中控制器内存容量的考虑，需要存放路灯的参数信息、注册信息等。

3 基于道路约束的路灯组网算法

不同的聚类分析方法适用于不同的数据聚类应用场景，通常需要考虑数据量大小和数据特征属性来选择合适的聚类算法。路灯数据是空间型数据，文献［1］中，提出的eb-cls聚类算法可以有效找出基于道路网络中的对象聚类的结果。然而，由于在ZigBee无线传感网络中，路灯的集中控制器所能存储的路灯信息是有限的，同时，相邻节点间的有效传输距离是受环境影响的。

SLCNARN 算法是建立在eb-cls 算法的基础上，增加了对基于环境的网络距离定义、路灯集中控制器容量以及对路灯基于道路分布特点的考虑，并通过对比实验验证该算法的可行性。SLCNARN算法根据路灯对象带状分布以及ZigBee 结点组网的特点，以路灯通信距离和路灯集中控制器容量作为聚类分裂阶段和合并阶段的条件，这样在分裂阶段只需要计算路段（边）的长度，对超出集中控制器容量距离μ（μ=θ×路灯间距）的聚类进行分裂，减少了时间消耗，也提高了SLCNARN 聚类算法的精度。下面几个小节主要对SLCNARN算法进行介绍说明，并通过实验进行算法验证。

3.1 eb-cls算法

eb-cls算法［1］，主要分为初始化阶段、分裂阶段和合并阶段。它是将两种典型的层次聚类方法（自顶向下分裂的层次聚类方法和自下向上的凝聚层次聚类方法）相结合，利用对象包含边的信息，从中间层次将对象划分为初始聚类，再分别向下层和上层进行层次的分裂和合并，这种方法适用于数据量大的数据，聚类效率较高。

eb-cls 算法在分裂阶段时，需要遍历每条边上面的对象，对相邻对象距离相似度不满足条件的聚类，在两个对象之间将聚类块划分裂成两个聚类；在合并阶段时，也是根据相邻聚类间的网络距离进行聚类的合并。而对于路灯对象来说，它们在道路上是等距分布的，即同一道路边上的对象是相似的。

因此，本文提出的SLCNARN算法，根据路灯对象带状分布以及zigbee 结点组网的特点，以路灯通信距离和路灯集中控制器容量作为聚类分裂阶段和合并阶段的条件，这样在分裂阶段只需要计算路段（边）的长度，对超出集中控制器容量距离μ（μ=θ×路灯间距）的聚类进行分裂，减少了时间消耗，也提高了SLCNARN 聚类算法的精度。下面几个小节主要对SLCNARN 算法进行介绍说明，并通过实验进行算法验证。

3.2 SLCNARN算法

SLCNARN 算法本质上是基于层次聚类的算法，大致分为以下三个阶段：聚类初始化阶段、聚类分裂阶段、聚类合并阶段。

1）聚类初始化阶段。将同一个路段上面的路灯划分成同一个聚类，初始聚类的个数即为网络边的个数。

2）聚类分裂阶段。主要是依次遍历各个路段，依次分裂大的聚类块为较小的聚类块。具体来说，对于每个初始的聚类，使它的网络边的长度不大于μ。另外，为了优化接下来的聚类合并，还需要为每个聚类块指定其满足μ和θ有效结点。

3）聚类合并阶段。根据聚类块之间的距离相似度，同时，需要结合聚类合并之后路灯节点总数，使它的和不大于集中控制器的最大负荷。具体来说，就是需要反复合并每个结点周围的聚类，直到合并到最大的聚类结果。

3.3 算法步骤

4 实验结果分析与讨论

4.1 实验配置和数据集

实验的硬件环境配置为Intel（R）Core（TM）i5-4200M CPU 和8G 内存的PC，软件环境为win10平台，所有代码使用C#实现。本文使用A 市中心城区的路网结构及其路灯终端节点安装位置作为实验数据，根据所在环境特征，其终端及其对应的综合环境影响因子γ分布如图2所示。

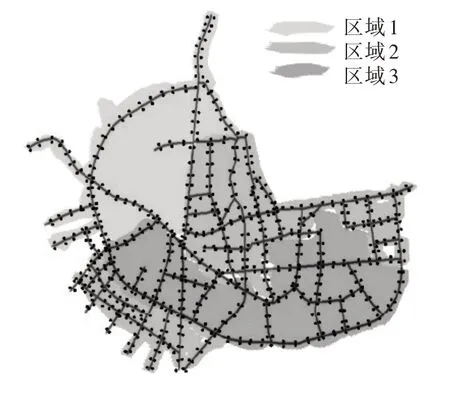
图1 路网结构及其综合影响因子示意图

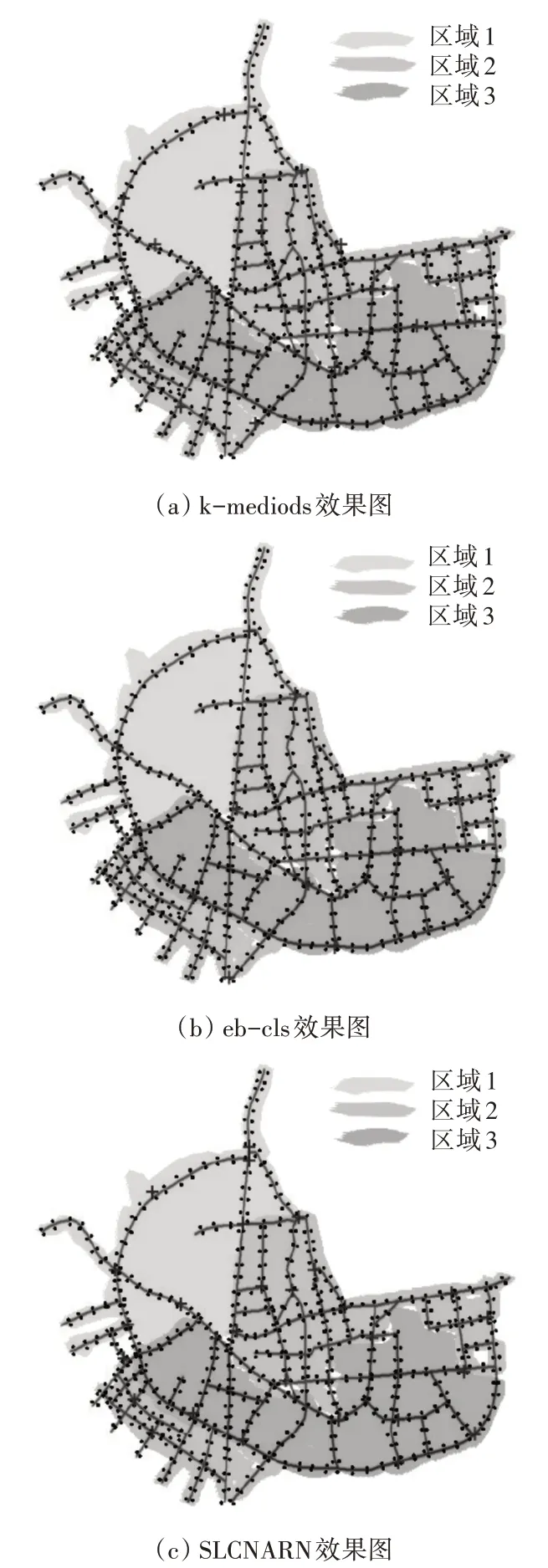
图2 k-mediods、eb-cls和SLCNARN效果图

根据地理环境特征，将该市路网结构图大致分成3个区域，其中，区域1，以高速公路为主，地带较为空旷，树木遮挡较少，故综合影响因子取值为γ=0.9；区域2，以市区街道为主，树木建筑较多，路灯有较多藏在树中，故综合影响因子取值为γ=0.6；区域3，有一定程度低矮建筑和树木遮挡，故综合影响因子取值为γ=0.8。

根据我国《城市道路照明设计标准》［12］以及对集中控制器的内存容量等因素的考虑，将实验参数设置如下：集中控制器的最大容量设置为300，路灯间距设置为25m，相邻节点最大通信距离设置为200m。

4.2 实验结果与分析

为了评估该算法的性能，我们通过将此算法分别与eb-cls算法和k-mediods算法的分类方法进行比较。本小节主要从算法的实现效果和算法效率进行对比验证。

SLCNARN 算法效果验证：路灯对象的聚类效果主要从路灯对象的整体性和聚类的精度两方面综合考虑。

一方面是路灯对象的整体性。道路路灯是基于道路分布的，因此，需要考虑路灯控制时候按道路开关的一致性和连贯性，即一条道路（边）被聚类到的对象个数越少越好。在本实验中，通过对比不同算法数据集中每条边上的聚类总数与道路边总数的比值来衡量路灯对象的整体性。

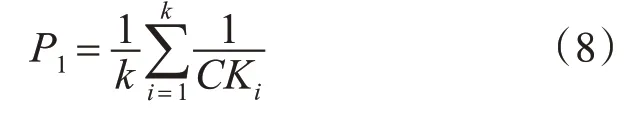
其中，k表示道路边的数目，CKi表示每条边上面聚类的个数，表示每条边的“整体性”。

另一方面是聚类的精度。聚类精度是检测聚类质量的重要指标。路灯对象在聚类的过程中，需要将每个对象都“分配”到聚类中去，同时，需要满足聚类中心容量（集中控制器的容量）的要求。在本实验中，我们通过计算对象数与集中控制器容量的百分比作为衡量聚类精度的指标［14］，其公式如下：

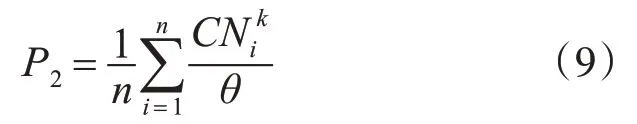
其中，n 表示聚类的数目，CNi表示第i 个聚类中的对象个数，θ是集中控制器最大容量，是第i个聚类的精度值，P2的取值是所有聚类的平均精度值。

通过对路灯对象整体性和聚类精度两方面的考虑，分别应用式（8）和式（9）对P1和P2值进行比较，实验结果如表2、表3 所示，由表2 可知，eb-cls算法与SLCNARN算法，路灯对象的整体性相似，这是由于两个算法在聚类初始化阶段都是以路灯对象所在边作为初始化聚类，在分裂阶段中eb-cls算法由于相邻路灯对象之间距离等距，分裂出的聚类有限，SLCNARN 算法由于根据集中控制器容量进行聚类分裂，分裂出的聚类也比较有效，因而两个算法最终的整体性相似；SLCNARN 算法与k-mediods 算法相比，聚类路灯对象的整体性较好，整体性数值也较为稳定，由表3 可知，SLCNARN 算法的聚类精度高于eb-cls 算法，这是由于eb-cls 算法在聚类的过程中会删除孤立的点，而在k-mediods 算法中，聚类簇数和中心点的选择对结果影响很大。

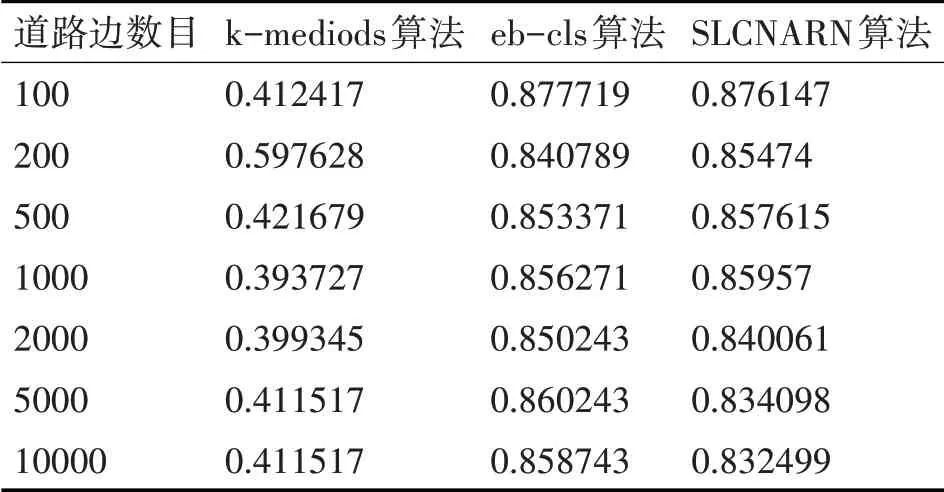
表2 路灯对象整体性比较

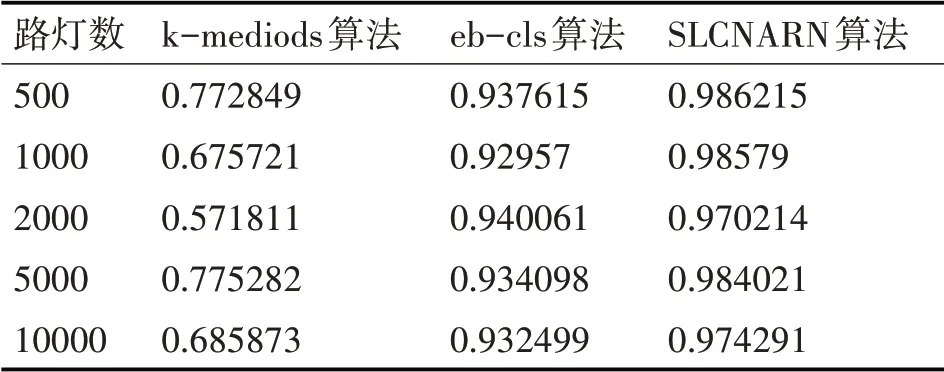
表3 聚类的准确率比较

如图2 所示，（a）是k-mediods 算法聚类结果，生成了23 个聚类中心点即集中控制器摆放位置；（b）是eb-cls 算法聚类结果，生成了13 个聚类中心点，聚类中心数量与（a）和（c）相比较少，每个聚类中心点所聚合的终端节点数量大于集中控制器容量阈值；（c）是SLCNARN 算法聚类结果图，生成了28 个聚类中心点，中心点位置主要集中在路口交叉处，便于管理。

SLCNARN 算法效率验证：基于上述的实验配置和数据集，通过改变路灯节点的数量值，对SLCNARN 算法、eb-cls 算法以及k-mediods 算法执行时间进行比较，结果如图3 所示，SLCNARN 算法执行时间要比eb-cls 算法要低，远小于k-mediods算法，这是由于SLCNARN 算法是基于道路边进行算法的分裂过程，同时考虑了路灯对象的空间特性和传播特性，减少了聚类算法的操作过程，而k-mediods 算法运行的时间由它的复杂度O(k(n-k)2)决定的。

图3 执行时间比较

通过上述实验的分析验证可以看出，SLCNARN算法可以有效地找出路灯对象聚类的结果，计算出集中控制器的摆放位置；而且算法的效率较高，在路灯集中控制器的选址上具有较高的应用价值。

5 结语

本文提出的路灯组网算法在综合考虑道路、环境等因素的前提下，将路灯节点进行聚类分簇，计算路灯集中控制器的摆放位置，同时通过实验，与K-mediods 算法、eb-cls 算法进行对比，实验结果表明，该算法能够有效降低劳动强度，为集中控制器的安装提供理论依据。