基于非等量采样的伪码同步技术研究

华 博, 毛忠阳, 康家方,*, 刘锡国, 魏靖怡

(1. 海军航空大学航空通信教研室, 山东 烟台 264001; 2. 中国人民解放军91980部队, 山东 烟台 264001; 3. 中国人民解放军91876部队, 河北 秦皇岛 066206)

0 引 言

由于伪随机序列具有良好的相关特性,因此基于伪随机噪声(pseudo-random noise, PN)序列的同步方法在数字通信系统中有广泛的应用。常用的同步算法包括最大似然(maximum likelihood, ML)、匹配滤波、延迟锁相环、离散傅里叶变换(discrete Fourier transform, DFT)/快速傅里叶变换(fast Fourier transform, FFT)等方法。最大似然法也称全并行捕获法,工作原理是将接收信号与个不同相位的本地PN码同时相关,同时检测得到个相关值,选择相关值最大的一路作为本地同步PN码,从而实现接收信号的解调解扩。这种方法的缺点也很明显,为同时获得个相关值,接收端需要使用个相关器,增大了接收端设备的体积,而且同步精度也只能达到1/2码片宽度。匹配滤波法是将本地PN码作为滤波器的抽头系数,当接收信号经过滤波时,若接收信号与滤波器的PN码相位一致,则会产生一个尖峰脉冲,利用门限检测出尖峰脉冲,即可作为同步指示信号。匹配滤波的优点是建立同步时间短,但由于实际硬件资源的限制,抽头系数不能太长。虽然这些方法都能实现同步,但是忽略了数字通信系统的采样过程会恶化PN码同步精度。

1995年Cheng等在分析全数字数据转换跟踪环时指出,当采样速率与码片速率之比(简称采样比)为整数时,同步精度受限于采样时间间隔,并首次提出非等量采样(non-commensurate sampling, NCS)的概念,即采样比为非整数。随后Quirk等指出,虽然NCS后每个码片包含的采样点数不再相同,但是采样点相对于码片的位置具有周期性,并在研究NCS技术对PN码跟踪环路影响的基础上,给出了系统稳态误差方差的表达式,但没有进一步说明如何选取最优采样比。柯颋等针对NCS采样率的选取策略,给出了定量性能评估指标及计算方法,利用评估指标完成数字接收机的设计,但未给出PN码跟踪环路的时间鉴别力与采样频率之间的解析表达式,因此,在设计数字接收机时,仍需要花费大量时间利用评估指标对其相关参数进行调试。Xu等定性分析了采样比与同步精度之间的关系,并提出了基于单位增量的NCS采样率选取方法,不过该方法仅对采样比有宽松的要求,对相关长度的要求较严格,这增加了系统设计的难度。Jin等分析了影响数字接收机同步精度的主要因素——S曲线零偏置,提出了通过补偿零偏置以消除相关曲线不对称带来的时延估计误差;并提出了通过获取特殊采样比实现零偏置自抵消,从而实现无补偿的信道时延估计。然而,零偏置补偿算法不仅会增加计算量,还会引入新的误差,导致同步精度的下降;同时特定的采样比并不容易在硬件上实现。随后Jin等研究了热噪声对弱信号跟踪性能的影响,将NCS技术与亚奈奎斯特采样技术相结合,在不降低系统性能的情况下,实现对时延的高精度估计。

Yang等推导出NCS技术下的PN码离散自相关函数,研究了采样比、积分周期以及相关间隔对离散自相关函数的影响,分析了不同采样比与自相关函数之间的关系,提出了与典型载噪比(carrier to noise ratio, CNR)相适应的采样率,但是整个分析过程中仅考虑了少数几个采样率,结论不具有普适性。Ma等将S曲线零偏置的最大值和标准偏差作为NCS同步性能评估指标,利用评估指标寻找零偏置最大值和标准差同时达到最小的采样比,即为满足多种约束条件的最优采样比。

现有研究报道主要是对NCS与同步精度关系的表述,旨在利用各种评价指标或约束条件寻找最佳采样率,而实际上满足多种约束条件的采样率并不多。同时,大多评估准则仅考虑了在理想情况下的NCS采样比的同步性能,但实际中各种因素如信道噪声、PN码周期、接收机前端滤波器带宽等都会影响PN码同步精度,从而增加数字接收机的设计难度。因此,关于如何快速判断NCS采样率所具备的同步精度,摆脱各种评估准则或约束条件的限制,降低数字接收机设计的难度,是一个重要的研究方向。本文通过推导NCS条件下PN序列相关函数解析表达式,探索影响NCS采样比同步精度的根本因素,提出NCS采样比选取的简易方法。同时,引入最大绝对误差和均方误差(mean square error, MSE)作为衡量NCS条件下PN码同步性能的指标,并分析PN码周期、接收机前端滤波器等因素对同步精度的影响。

1 等量采样技术同步性能分析

为了从接收信号中提取数据或定时信息,必须知道接收信号与本地模板信号之间的相对相位,并通过调整本地模板信号,使得两者相位一致,这个过程称为同步。在数字通信系统中常以PN序列作为同步头,利用其良好的相关特性实现同步,而在进行同步之前必须先对接收信号“数字化”处理。一般情况下接收机采用的采样率都是码片速率的整数倍,将这种采样方式称之为等量采样。对于任意初始同步偏差,其采样点位置与码片之间的关系,如图1所示。

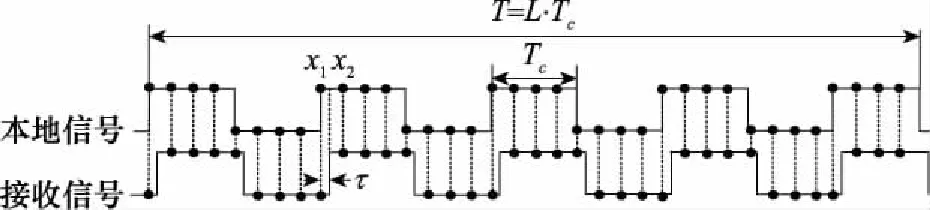
图1 等量采样过程示意图Fig.1 Schematic diagram of equal sampling process

在图1中,实线为模拟信号,为同步偏差。从图1中可知,当0<<,接收信号与本地信号的所有采样点幅值均不发生变化,导致相关函数始终保持不变。因此,等量采样技术会限制数字接收机的同步精度。即便采样间隔非常小,仍然存在无法辨别的同步偏差。在数学上,这种同步偏差可以用相关形状的“阶梯”现象来解释。为便于分析,且不失一般性,假设接收信号是未经采样的周期为的PN序列,不考虑载波偏差的影响,可将接收信号表示为

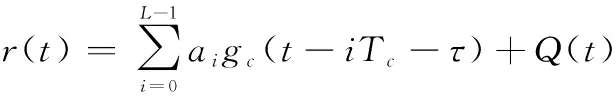
(1)

式中:为PN序列的码片周期;表示第个幅值为±1的码片;()为持续时间为的单位脉冲;()为高斯白噪声,其功率谱密度为2。

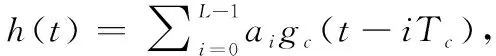
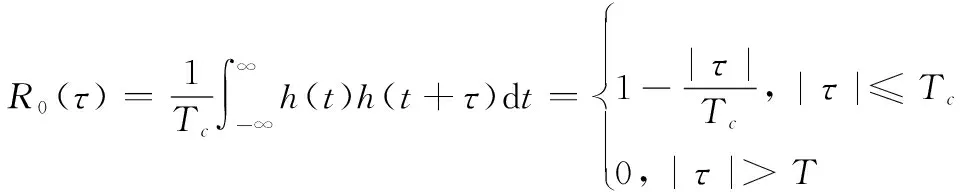
(2)

当0<<时,接收端相关器输出的归一化相关函数可以表示为

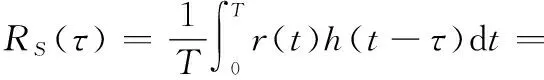
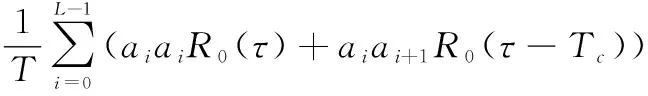
(3)

其中,相关积分时间=·。结合式(2)和式(3)可知,接收端相关器输出的归一化相关函数是同步偏差的单值线性函数。因此,值的变化可以准确反映在相关函数()的变化中。但在数字通信系统中,接收机将以固定的时钟对()进行采样,采样后的信号可以表示为

(4)

其中,=为采样间隔;为经采样后的同步偏差,即=+ϑ,而ϑ为剩余同步偏差。因此,采样后的相关器输出的相关函数为

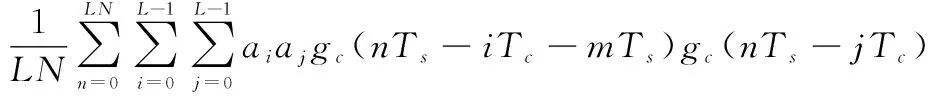
(5)

其中,矩形脉冲()的归一化自相关函数为

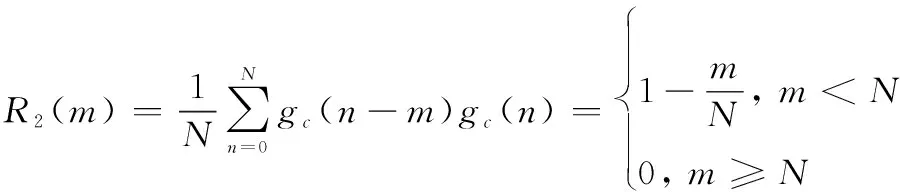
(6)

联立式(3)、式(5)、式(6)可得接收端相关器输出的归一化相关函数为

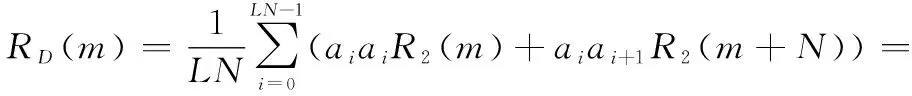
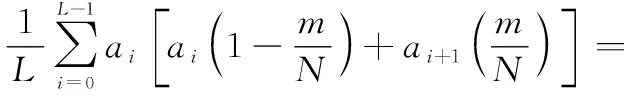
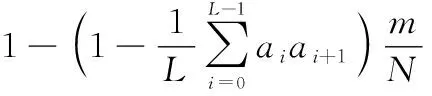
(7)

由式(7)可知,数字接收机的同步精度与采样总点数和同步偏差的采样点数有关。当采样率越高时,采样点数、越大,剩余同步偏差ϑ越小,通过相关函数对同步偏差的估计越准确,从而利于提高信号同步精度。假设在相同的采样率下,存在同步偏差<,经过采样=+ϑ,=+ϑ,根据式(7)可得1=2,显然由于采样过程的影响,导致不同的同步偏差出现相同的相关输出。当同步偏差=100时,不同等量采样比条件下的相关函数,如图2所示。

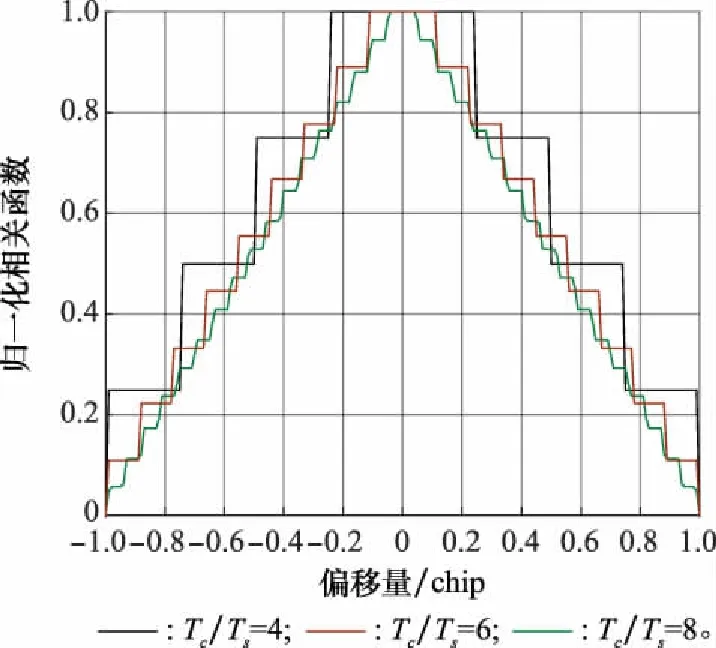
图2 等量采样下的相关函数Fig.2 Correlation function under equal sampling

从图2中可知,对于远小于采样间隔的同步偏差,PN序列的相关函数呈现阶梯状变化,即不同的同步偏差可能有相同的相关函数值,这会严重影响系统完成同步,造成接收机无法正确解调解扩。虽然通过提高采样率,可以提高系统同步精度,但当需要达到1%甚至0.1%码片宽度的同步精度时,采样率要达到码片速率的100倍、1 000倍甚至更高,这会消耗大量的硬件资源。因此,如何以较低的采样率实现较高的PN码同步精度是降低硬件资源消耗的关键,NCS技术为解决这一问题提供了新的思路。

2 NCS技术同步性能分析及选取准则

当采样率与码片速率的比值不是整数时,PN码同步精度将不再受采样间隔的限制,这种采样方式被称为NCS。经NCS技术处理的信号,其单个码片内的采样点位置分布不再固定,为量化这种情况,假设每个码元符号内的单个采样点距符号边沿的距离(称为采样点相位偏移量)为,如图3所示。

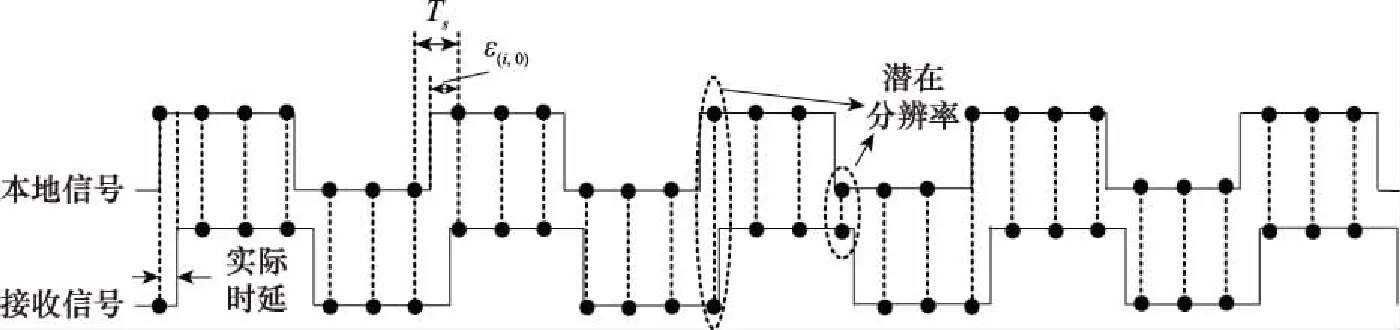
图3 NCS示意图Fig.3 Schematic diagram of NCS

(,0)=-(-((,0)-1))=(,0)-

(8)

其中,(,0)表示第个码片第1个采样点的位置索引。从式(8)可知,任意(,0)都满足不等式0≤(,0)<,而采样点位置索引满足关系式:

(9)

若将式(9)中采样比表示成最简分式,即=,且与为互质整数,则当=时,联立式(8)、式(9)可得

(10)

由式(10)可知,偏移量具有周期性,其循环周期为,这意味着在个码片后(,0)将重复出现。将第个码片中采样点分布表示为

(,)=(-(,0))+(,0)

(11)

因此,在NCS条件下,接收信号为

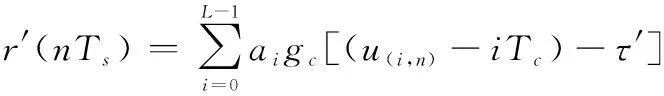
(12)

由式(3)可知,对于采样后PN序列的自相关函数本质是采样点幅值的乘加运算。因此,对于采样后的矩形脉冲信号,可以认为其自相关值就是采样点总数减去极性互异的采样点数。若时延′=+ϑ′,其中∈。当>0时,矩形脉冲的自相关函数为

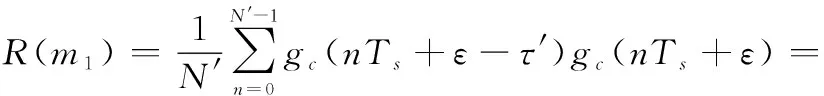
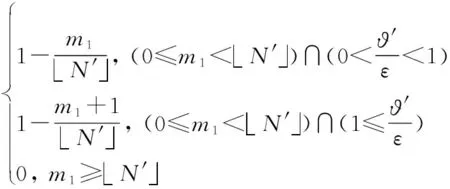
(13)

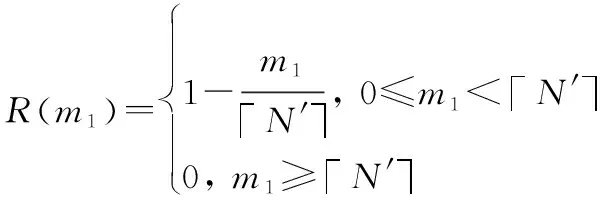
(14)

由式(13)可知,经NCS后的矩形脉冲,其自相关函数与偏移量有关。因此,对于接收信号而言,NCS条件下的同步偏差可以表示为=++Δ,其中0≤Δ<,为使整数≥1的最大偏移量。在不考虑循环周期内首个码片的偏移量时,循环周期内其余偏移量呈单调递减分布。因此,当0<≤时,结合式(3)、式(13)可得,NCS时PN序列的相关函数可以表示为

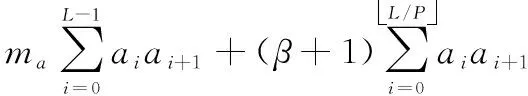
(15)

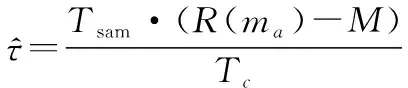
(16)

除了偏移量会对相关函数产生影响,PN序列周期、偏移量循环周期也会对相关函数产生影响。由式(15)中可知,当PN序列周期远小于偏移量循环周期时,意味着经采样后的序列中不存在偏移量循环周期。因此,其相关函数可以表示为

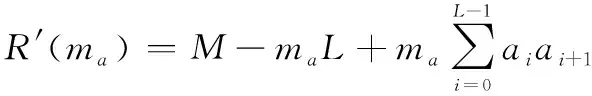
(17)

通过对比发现,经归一化后的′()与式(7)相同,这表明当PN序列周期远小于循环周期时,NCS技术将不具备高精度同步能力。

当采样比固定时,偏移量代表了该采样比所能达到的最高同步精度,但由于的随机性,无法通过理论计算来获得该采样比的同步精度,只能通过实验的方法检测其同步精度,而这一过程往往需要消耗大量的时间。但从式(10)、式(15)中可知,偏移量的大小与偏移量循环周期有关,结合图3可知,NCS技术的实质是利用循环周期将原整数倍采样间隔进一步细分成等份,使同步精度再提高倍,即

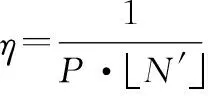
(18)

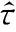
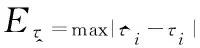
(19)

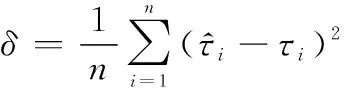
(20)

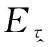
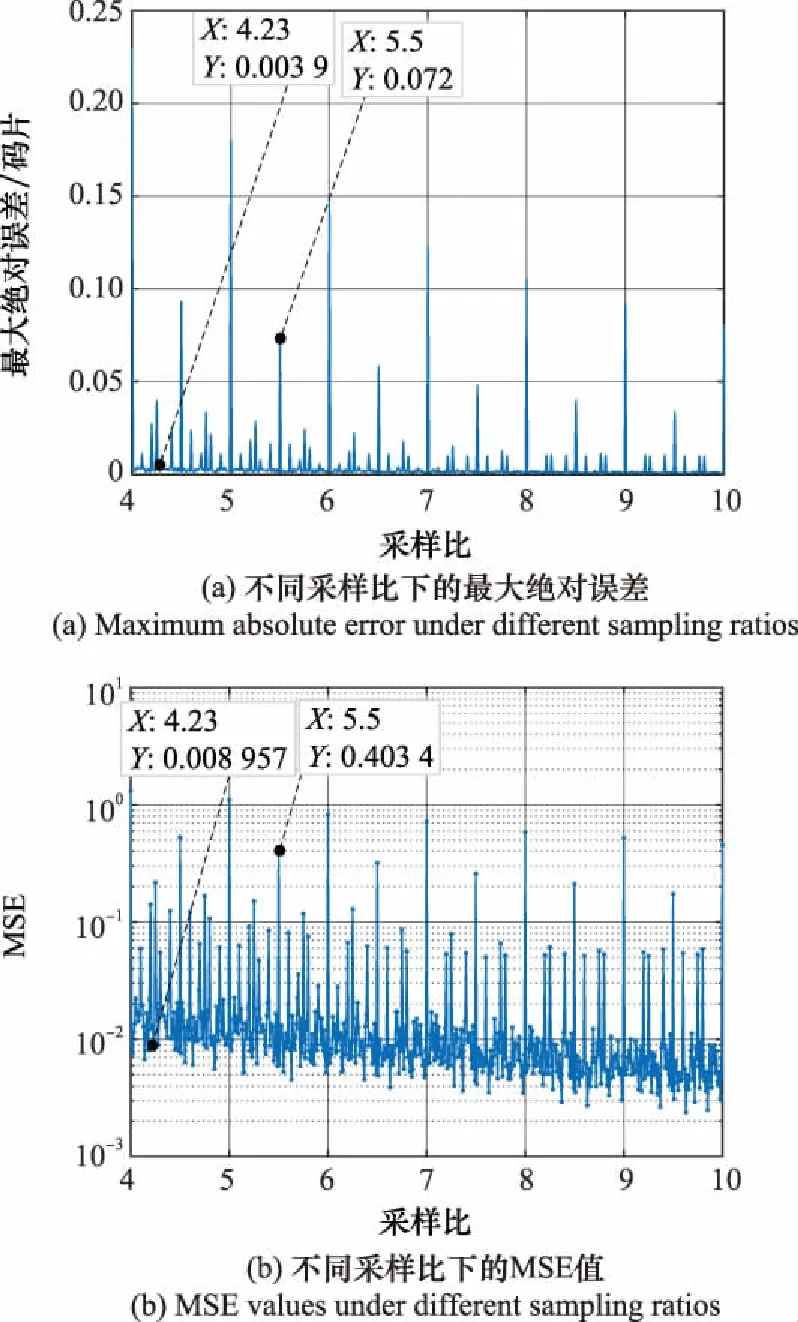
图4 定量评估指标Fig.4 Quantitative evaluation indicators

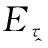
综上所述,随着采样比的增加,PN码同步误差逐渐降低,但是当采样比恰好等于码片速率的整数倍时,接收机同步误差会陡然增大。从局部变化看,同步误差的起伏变化毫无规律,这种变化是由NCS采样比的精度因子决定的。

3 NCS同步性能仿真分析

为进一步分析NCS采样比的同步精度,验证理论分析的正确性,结合数值分析,对NCS技术的同步性能进行仿真分析。仿真条件及参数设置如下:

调制方式:BPSK调制;

同步方式:匹配滤波同步;

码片周期:=1;

同步偏差:=100;

伪随机序列:1 023位序列。

3.1 NCS同步精度

合适的NCS采样比对系统同步性能有着重要的影响,根据第2节分析,NCS采样比可分为两种情况:① 精度因子小于预设时延;② 精度因子大于预设时延。因此,分别取不同类型的采样比:4、4.23、4.5、5.5,对其相关函数进行仿真。仿真结果如图5所示。

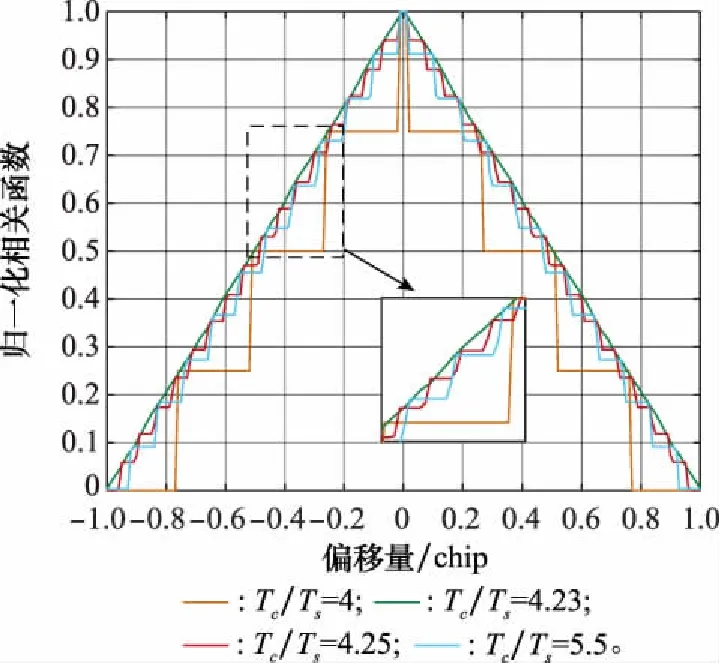
图5 不同采样比下的相关函数Fig.5 Correlation function under different sampling ratios

从图5中可知,采样比之间的差值并不大,但是相关函数存在明显的区别。当采样比=4时,相关函数呈现明显的“阶梯”状;当采样比=423时,相关函数呈现理想三角形;而采样比=425的相关函数再次呈现“阶梯”状；当采样比继续增加到5.5时相关函数的“阶梯”状愈加明显,说明单纯增加NCS采样率并不一定能提高同步精度,而盲目地选取NCS采样率会增加系统的设计难度。根据式(18)可得,采样比4.23、4.25、5.5的精度因子分别为0.002 5、0.062 5、0.1,通过对比发现,只有采样比4.23的精度因子小于1/100的同步偏差,结合图5的相关函数可知,只有当精度因子小于预定的同步偏差,NCS采样比才能达到预期同步精度。因此,精度因子可以作为选取NCS采样比的重要依据。

对于通信系统而言,信道噪声是必须考虑的因素。一般情况下,信道噪声被认为是服从零均值的正态分布,在没有信道噪声影响下,PN码的同步精度完全取决于循环周期。信道噪声会改变PN码的相关函数,从而对同步过程产生一定影响。因此,在同步偏差分别为100和/1 000的情况下,对不同类型采样比的同步精度进行仿真,为便于观察,仅标注具有分辨力的采样比,仿真结果如图6所示。

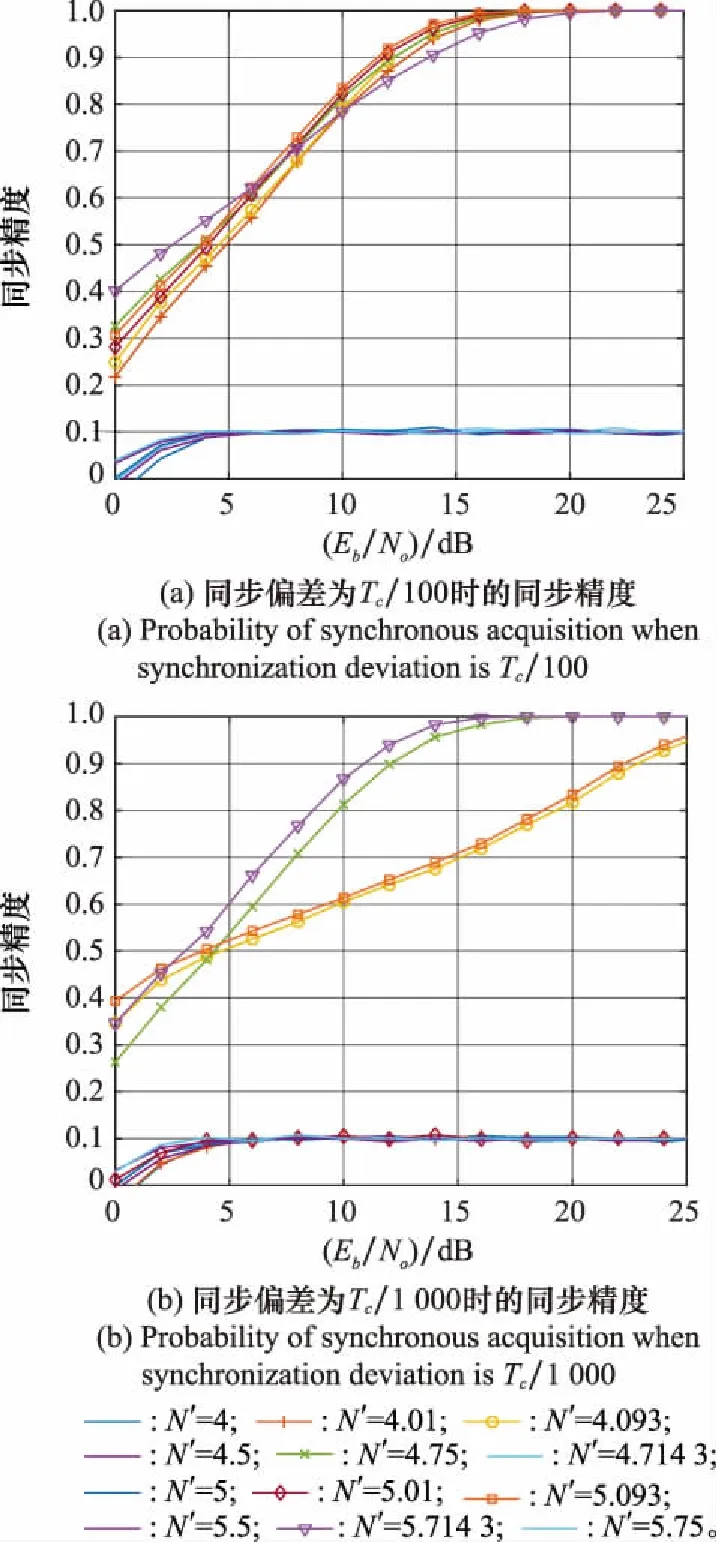
图6 不同采样比下的同步精度Fig.6 Probability of synchronous acquisition under different sampling ratios

从仿真结果可知,当同步偏差为/100,采样比分别为4.01、4.093、4.714 3、5.01、5.093、5.714 3时,同步精度随着信噪比的增加而增加;当同步偏差为/1 000,除采样比4.01和5.01的同步精度降低到0.1,其他采样比的同步精度均未发生变化。这是因为采样比4.01和5.01的精度因子分别为0.002 5、0.002,两者的精度因子均小于1%,而大于0.1%,因此,这两种采样比能分辨/100同步偏差,但不能分辨/1 000同步偏差。仿真结果进一步说明,NCS采样比的同步偏差分辨能力与精度因子有直接关系,精度因子可以作为NCS采样比选取的可靠依据。

3.2 PN码周期及接收机前端滤波器对同步精度的影响

根据NCS条件下的PN序列相关函数表达式可知,当PN序列周期小于码相位偏移量循环周期时,PN序列的相关函数会发生变化,当PN序列周期过小时,将会影响NCS采样下的PN序列同步精度。因此,对周期为15、63、255、1 023的序列的最大绝对误差进行仿真,仿真结果如图7所示。

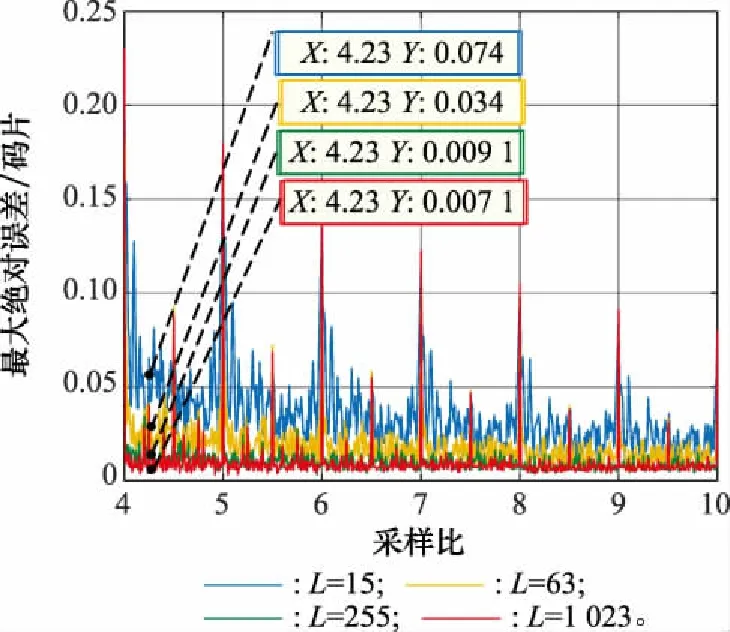
图7 不同码长下的最大绝对误差Fig.7 Maximum absolute error under different code lengths

从仿真结果可知,在整体变化上,不同码长下的最大绝对误差的变化趋势相同;在相同NCS采样比的条件下,最大绝对误差随着序列长度的增加而降低,当采样比为4.23,长度为15、63、255、1 023的序列对应的最大绝对误差分别为0.041、0.034、0.009 1、0.007 1,通过比较可知,只有在码长为255和1 023时,同步最大绝对误差值才小于1%。而根据第2节的理论分析,采样比4.23的偏移量循环周期为100。因此,只有当PN码序列的长度超过循环周期时,NCS采样比才实现高精度同步。

综上所述,PN码序列周期影响了偏移量循环周期,当PN序列的周期过短时,偏移量循环周期将不存在,从而降低NCS技术对微小同步偏差的分辨能力。因此,采用周期较长的PN码序列有助于降低同步误差,提高同步性能。

当PN序列具有无限长的周期和理想的自/互相关特性时,其相关函数是一个等腰三角形,但实际信号的发射与接收都需要进行带限滤波处理,在经过接收机前端滤波器处理后,接收信号变成带限信号,本地解扩信号未经过滤波器处理,是一个无限带宽的信号,对两个信号做互相关处理时,其相关函数将会发生改变,从而对同步精度产生影响。因此,对不同带宽下的PN码同步最大绝对误差进行仿真,结果如图8所示。

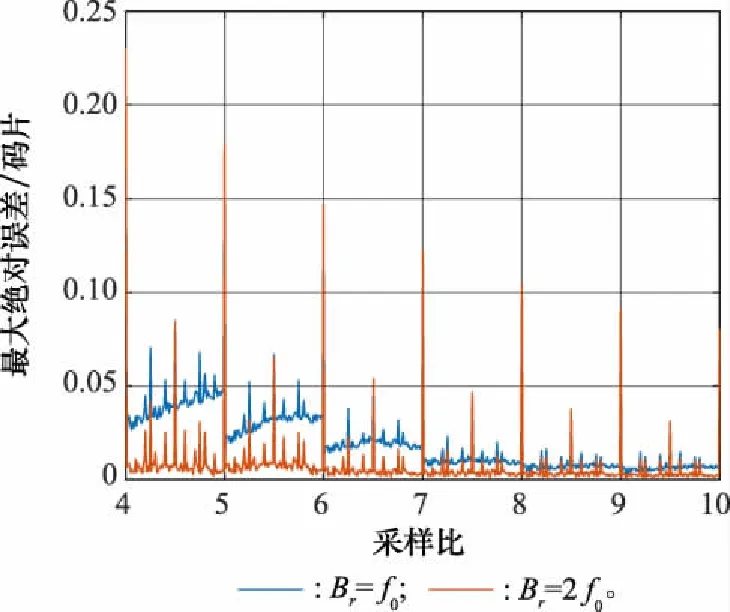
图8 不同带宽下最大绝对误差Fig.8 Maximum absolute error under different bandwidths

从仿真结果可知,不同带宽下的最大绝对误差存在一定差异,滤波器带宽=的最大绝对误差明显大于=2的最大绝对误差,但随着采样比的增加,这种差距逐渐缩小。这主要是带限滤波器降低了接收信号功率,改变了PN序列相关函数,与理想相关函数相比,经滤波的相关函数趋于平滑,而且滤波器带宽越窄相关函数越平滑,从而造成最大绝对误差值增大。不过,带限滤波器并没有改变NCS采样序列的精度因子,当采样比>7时,不同带宽下的最大绝对误差值相差仅0.004,说明当采样比提高到一定程度,PN序列的同步精度将会得到改善,因此可以通过提高NCS采样比来降低接收机前端滤波器的影响。

4 结束语

本文推导出了NCS技术下的PN序列相关函数的解析表达式,研究发现不是所有的NCS采样比都具备高精度同步性能,提出了基于精度因子的NCS采样比快速选取方法。理论分析和仿真结果表明：① 码相位偏移量循环周期是决定NCS采样比同步精度的关键因素,循环周期是NCS采样比最简分式中的分母,循环周期越大,所能实现的同步精度越高,当采样比是无理数时,理论上能实现无限精度,但实际受PN序列长度的限制,并不能实现无限精度;② 码相位偏移量循环周期并不能直接作为选取NCS采样比的依据,因为NCS技术的实质是在原整数倍采样间隔的基础上,更进一步将采样间隔细分成等份,从而使同步精度再提高倍,因此,将这两个参数相结合得到新的参量——精度因子,利用精度因子作为NCS采样比选取的依据,当精度因子小于预设的同步偏差时,PN序列的同步精度才能达到预期效果;③ 接收机前端滤波器通过改变PN序列的相关函数,从而对同步精度产生影响,但可以提高采样率来抵消前端滤波器的影响。本文提出的精度因子,可以快速判断不同采样比的同步精度,省去了繁琐的评估准则和约束条件,缩短了通信系统的设计周期。NCS技术的应用将以较低的硬件资源消耗获得较高的同步精度,为数字通信系统的设计提供理论指导。