高超声速飞行器新型攻角约束反演控制

韦俊宝, 李海燕, 李 静

(海军工程大学兵器工程学院, 湖北 武汉 430033)

0 引 言

由于高超声速飞行器在军事和民事方面具有巨大的应用前景,引起了世界广泛的关注。而飞行控制技术作为发展高超声速飞行器的关键技术,是实现飞行器跟踪轨迹和稳定飞行的基本保障,因此研究高超声速飞行器的控制系统设计对于其发展具有十分重要的意义。

目前,关于高超声速飞行器控制技术的研究已经取得了一定的成果。反演法、动态逆控制、滑模控制以及轨迹线性化等先进控制方法在高超声速飞行器控制器设计中均得到了应用。其中,反演控制作为一种解决非线性和不确定控制问题的有效控制技术,通过将高超声速飞行器动力学分解为速度子系统和高度子系统,可实现其控制器设计。

尽管高超声速飞行器的反演控制器设计已经取得了较大的进展,但对于攻角约束问题没有足够的重视。高超声速飞行器在实际飞行中,为了保证超燃冲压发动机的正常工作,需要攻角幅值满足一定的约束条件,否则会造成进气道不启动以及热力壅塞等问题,严重降低飞行性能。目前,大多文献利用Barrier函数来处理攻角约束问题。文献[7-9]基于Barrier函数将跟踪误差约束在一定范围内,却忽略了对攻击指令的限制,从而容易出现攻角能实现指令跟踪却超出约束范围的问题。文献[10-13] 提出一种基于Barrier函数的自适应反演控制方案,首先利用Barrier函数约束攻角跟踪误差,然后通过构造饱和函数对攻角指令限幅,从而实现攻角约束。其中,文献[10]利用微分跟踪器估计限幅后攻角指令的一阶导数,却忽略了该指令在饱和值处不可导的问题。文献[11]通过分别约束俯仰角和航迹倾角来处理攻击约束问题,设计流程较复杂。上述关于攻角约束的文献中,所提出的控制方案需要假设攻角初始误差满足约束条件。在实际中,攻角初始误差难以精确得到,并且该值可能过大;而通过扩大约束范围使得初始误差满足约束条件,则会降低攻角的跟踪性能。另外,大多研究注重于攻角误差的稳态性能,忽略了其动态性能。而当跟踪误差具有良好的动态性能时,能够使得攻角快速跟踪上满足约束条件的指令,不仅攻角约束问题得到较好处理,而且能进一步提高飞行器的机动性能。

基于上述分析,本文针对考虑攻角约束的高超声速飞行器控制问题,提出一种受限指令滤波器与预设性能方法相结合的反演控制方案。与已有的研究工作不同,本文通过构造受限指令滤波器对攻角指令限幅,保证攻角指令的有界性;并通过设定指令初始值,无需假设初始误差满足约束条件。在此基础上,本文进一步考虑攻角的跟踪性能,采用预设性能方法对攻角跟踪误差进行约束。所提出的方案在解决攻角约束问题的同时,能够提高攻角跟踪误差的瞬态和稳态性能。最后对该方案的有效性进行了理论证明和仿真验证。

1 系统描述与预备知识

1.1 系统描述

高超声速飞行器纵向运动刚体模型为

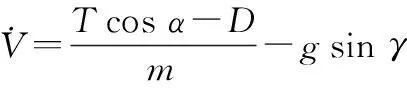
(1)

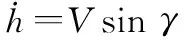
(2)

(3)

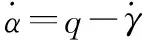
(4)

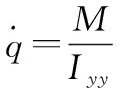
(5)

式中:速度、高度、航迹倾角、攻角以及俯仰角速度为刚体状态变量;为质量;为重力加速度;为转动惯量;、、、分别为推力、阻力、升力以及俯仰力矩,可描述为

(6)

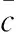
式(3)中的sin项数值远小于升力值,因此该项可以忽略。

系统模型的输出为速度、高度;控制输入为燃油当量比、升降舵偏角。结合模型式(1)～式(5)与假设1可知,速度的变化主要受燃油当量比控制;升降舵偏角通过直接控制俯仰角速率变化,进而控制攻角、航迹倾角的变化,因此飞行器高度变化主要受控制。为了便于控制律设计,通常情况下,模型式(1)～式(5)可分解为速度子系统和高度子系统:

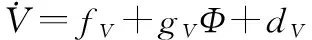
(7)

(8)

式中:

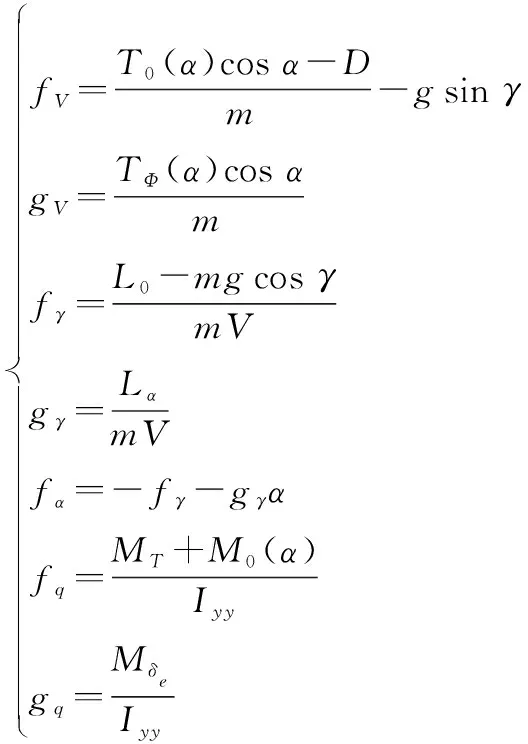
(=,,)为扰动项,包含外界干扰以及参数摄动,且有如下假设。

扰动项(=,,)连续且一阶导数有界。

1.2 预设性能

预设性能方法包括性能函数以及误差变换,是指跟踪误差收敛在一个预先设定的任意小区域内的同时,跟踪误差的收敛速度和超调量均满足预设条件,保证系统的瞬态和稳态性能满足预设要求。

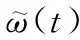
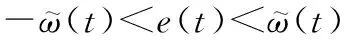
(9)

为将不等式约束转化为等式约束,建立等式

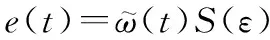
(10)

式中:为转换误差。定义转换函数为

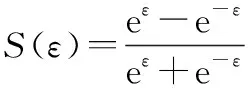
易知,()为光滑、严增可逆函数,满足:

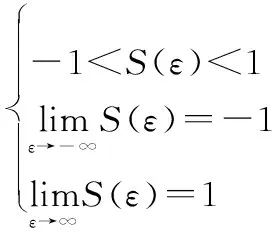
(11)

进一步,()的逆变换为

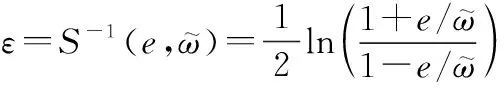
(12)

根据式(12),若始终有界,则不等式(9)成立,即系统跟踪误差不仅有界而且被限制在设定的范围内,从而保证跟踪误差满足预设的瞬态和稳态性能要求。

1.3 线性扩张状态观测器

考虑如下的一阶不确定系统:

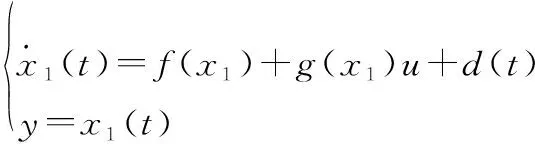
(13)

式中:()为不确定项,假设()连续且一阶导数有界。针对该系统,可以建立如下所示的线性扩张状态观测器(linear extended state observer,LESO):

(14)

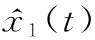
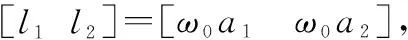
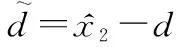
2 控制器设计

由于本文主要研究控制系统中的攻角约束问题。考虑到速度子系统结构较为简单、阶数较少,通过设计动态逆控制器可使其稳定跟踪指令,因此省略该子系统的控制器设计与仿真,而将研究重心放在含有攻角状态的高度子系统中。

针对高度子系统式(8),进行控制器设计。

首先定义高度跟踪误差=-,其中为高度指令。依据文献[10],航迹倾角指令取为

(15)

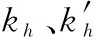
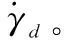
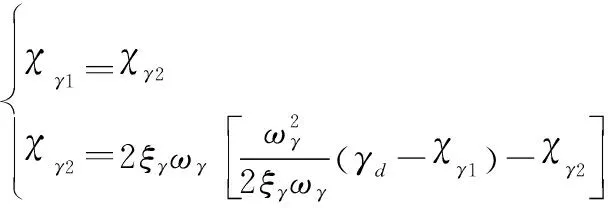
(16)

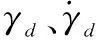
下面进行反演控制器设计。

定义航迹角误差=-以及补偿误差:

=-

(17)

式中:为待设计的辅助变量。结合式(8),对式(17)求导,得

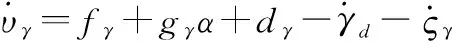
(18)

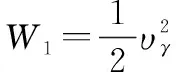
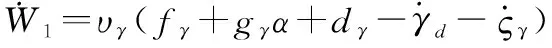
(19)

设计虚拟控制律为

(20)

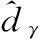
考虑攻角约束问题,首先对虚拟控制律进行限幅，并且为了保证限幅后指令的可导性,以便后续反演设计的顺利进行,构造如下受限指令滤波器:

(21)

式中:、均为正参数。饱和函数sat(·)如下:

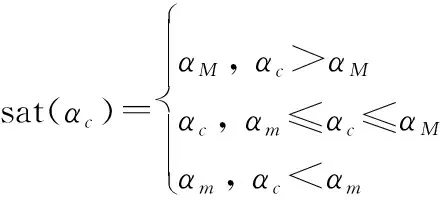
(22)

式中:常数>0、<0分别为攻角指令的上下限。取虚拟控制律=1。

式(21)中,取滤波器初值1(0)=(0),2(0)=-(+1)1(0)。目的是一方面使得攻角初始误差为零,满足特定的约束条件,无需假设初始误差满足约束条件。另一方面,通过赋予初始值,能够保证虚拟指令满足限幅条件,相关证明将在下文给出。

为了抵消攻角指令限幅造成的影响,设计如下辅助补偿系统:

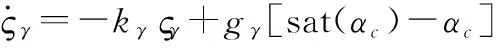
(23)

将式(20)、式(23)代入式(19),得

(24)

定义攻角误差=-并设定性能函数

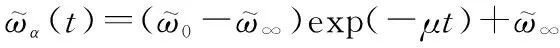
(25)

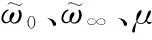
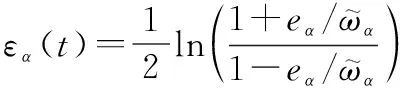
(26)

本文通过采用预设性能方法,将攻角跟踪误差约束在预设范围内。与文献[7-13]利用Barrier函数的方法相比,该方法在保证跟踪误差稳态性能的同时,能够进一步提高其动态性能。

结合式(8),对式(26)求导,得

(27)

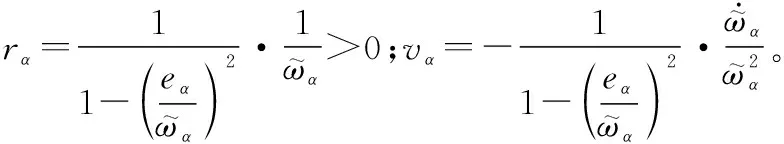
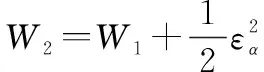
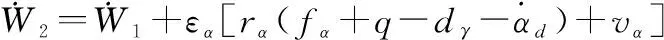
(28)

设计虚拟控制律为

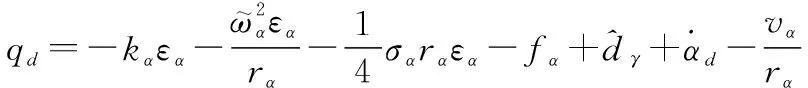
(29)

式中:、均为正参数。

将式(29)代入式(28),得

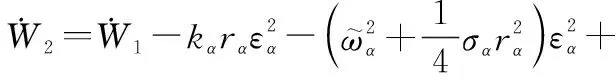
(30)

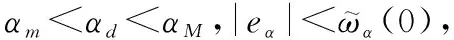
定义俯仰角误差=-,结合式(8)对其求导,得

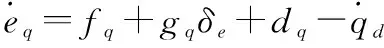
(31)

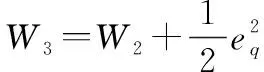
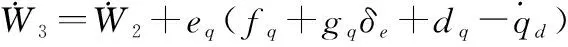
(32)

设计系统控制律为

(33)

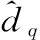
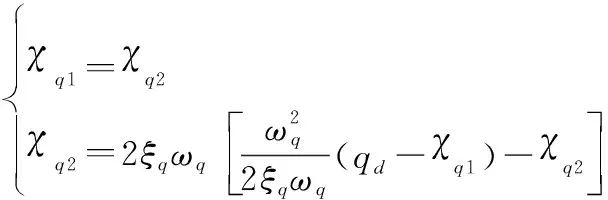
(34)

式中:、均为正参数。

结合式(33),式(32)变为

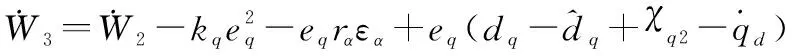
(35)

3 稳定性分析

针对所设计的控制器,可得到如下定理。

系统模型式(8)在参数摄动、外界干扰的情形下,基于假设1～假设3,采用式(33)所示的系统控制律,可得到如下结论:

(1) 高度子系统式(8)内所有跟踪误差最终一致有界;

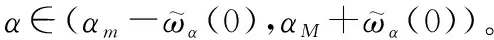
(1) 结论(1)证明

结合式(24)、式(28)以及式(35),将Lyapunov函数展开,得

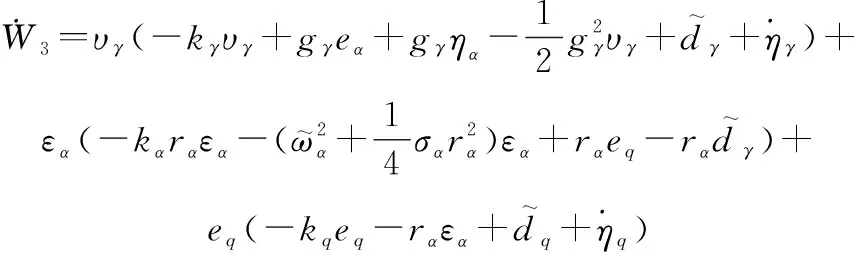
(36)

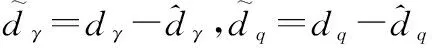
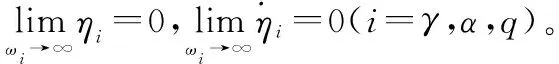
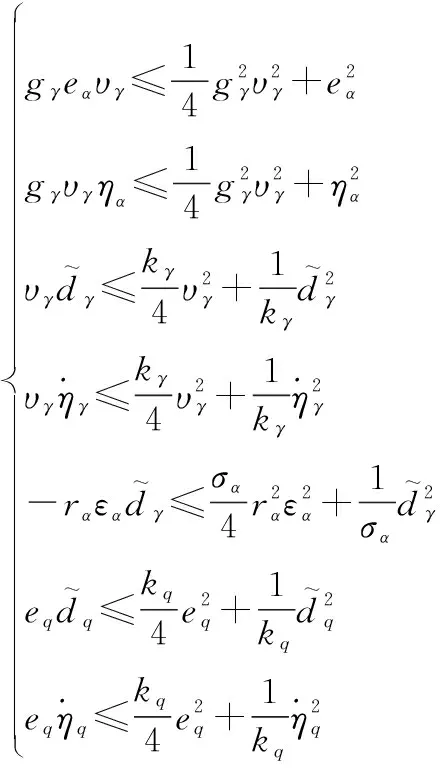
(37)

另外,对于式(10),利用中值定理可得

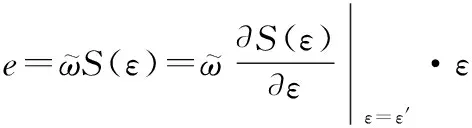
(38)

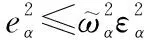
(39)

结合式(37)和式(39),式(36)可以化简为

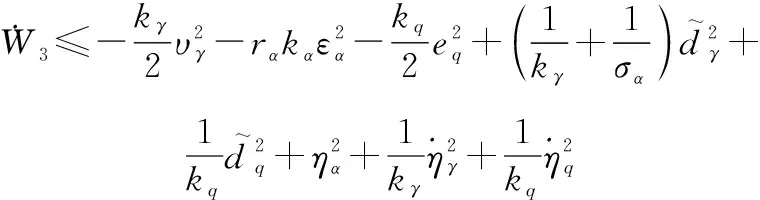
(40)

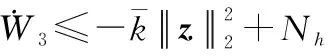
(41)

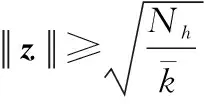
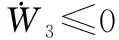
(42)

因此可以说明有界,根据的定义可得到,,有界。根据第12节,由有界可以得到有界且满足约束条件;当攻角指令退出饱和后,根据式(22),此时sat()=,则式(23)中→0,因此误差有界。

(2) 结论(2)证明

将式(21)进行变换,得到

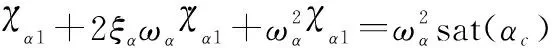
(43)

由于≤sat()≤,则式(43)可改写为

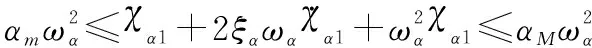
(44)

取=1,不等式(44)同时乘exp(),得

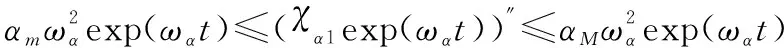
(45)

对不等式(45)积分,得

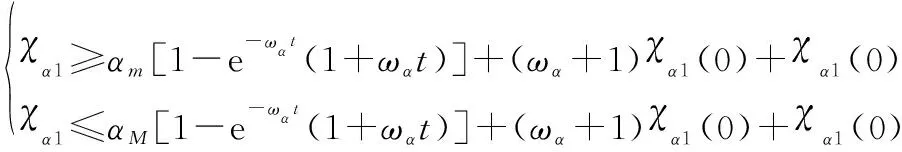
(46)

≤≤

(47)

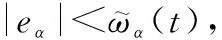
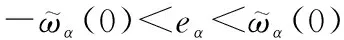
(48)

结合式(47)、式(48),并且=+,显然:

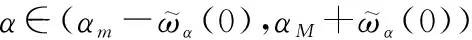
(49)

证毕

4 仿真分析

为验证本文提出的控制方案的有效性,以高超声速飞行器纵向运动模型式(1)～式(5)为对象,利用第2节的控制方法进行Matlab仿真。飞行器参数、气动参数取自文献[14],如表1所示,仿真控制器参数如表2所示。

表1 高超声速飞行器参数Table 1 Parameters of hypersonic vehicle

表2 控制器参数Table 2 Controller parameters

考虑系统参数摄动为+30%;扰动和包含的外界干扰分别设置为0002sin(02)和05sin(02);系统状态初始值设置为=7 702 ft/s,=85 000 ft,=0°,=1515 3°,=0°/s;攻角约束区间设置为∈[-6°,8°],则饱和函数边界值(单位为rad)分别设置为

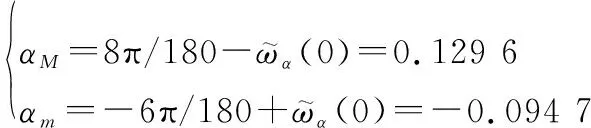
高度阶跃指令(单位为ft)设置为

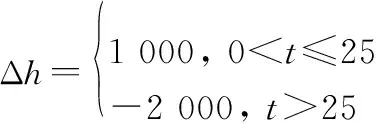
并通过如下滤波器产生指令信号:

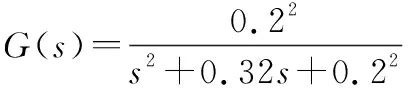
(50)

针对本文提出的控制方案(记为Case1),选取文献[10]所提出的控制方案(记为Case2)进行对比仿真。其中Case2仿真相关参数如下。

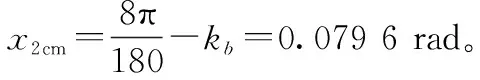
仿真结果如图1～图7所示。由图1～图4可见,Case1和Case2系统均能实现对指令信号的跟踪。显然,Case1的跟踪精度更高,控制效果更佳。为了保证初始误差满足约束条件,Case2系统需要扩大约束范围,而这一方面导致了跟踪误差值较大,造成攻角跟踪指令的效果不佳(见图3和图4);另一方面,使得攻角指令约束区间缩小,限幅后的攻角指令与理想指令之间误差增大(见图5),从而影响了整个高度子系统的跟踪性能。虽然Case2系统能够保证攻角始终满足约束条件,但攻角指令区间十分受限,系统跟踪性能较差,不利于实际应用。而对于Case1系统,显然攻角能够快速稳定跟踪上限幅后的指令的同时,始终处于攻角约束区间内(见图3)。攻角约束问题的解决,主要得益于以下两点:Case1无需考虑初始误差对约束条件的影响,并且跟踪误差快速收敛到零并保持稳定,显然跟踪误差的瞬态和稳态性能比Case2的更好(见图4);另外,Case1的攻角指令始终处于攻角约束区间内(见图5),这也验证了所构造的受限指令滤波器限幅指令的有效性。由图7可见,LESO对系统扰动能实现快速有效的观测,说明系统具有一定的抗干扰能力。综上,本文设计的控制方案在考虑参数摄动和外界干扰的情形下,使得系统实现了较好的指令跟踪效果;并且保证攻角满足约束条件的同时,提高了攻角的跟踪性能,较好地解决了攻角约束问题。这一仿真结果验证了该控制方案的有效性。

图1 高度、航迹倾角及俯仰角速率跟踪曲线Fig.1 Tracking curves of altitude、flight path angle and pitch rate

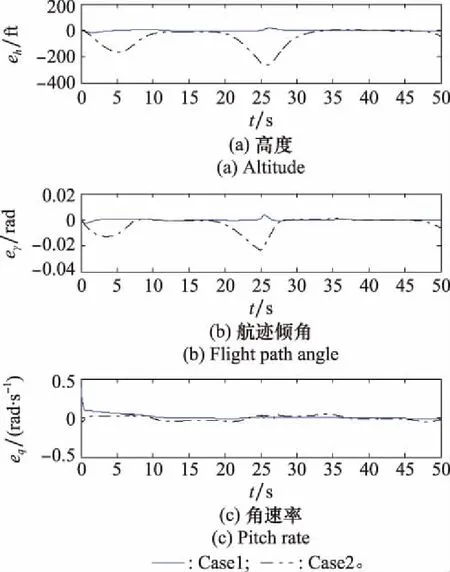
图2 高度、航迹倾角及俯仰角速率跟踪误差曲线Fig.2 Tracking error curves of altitude, flight path angle and pitch rate

图3 攻角跟踪曲线Fig.3 Tracking curves of angle of attack

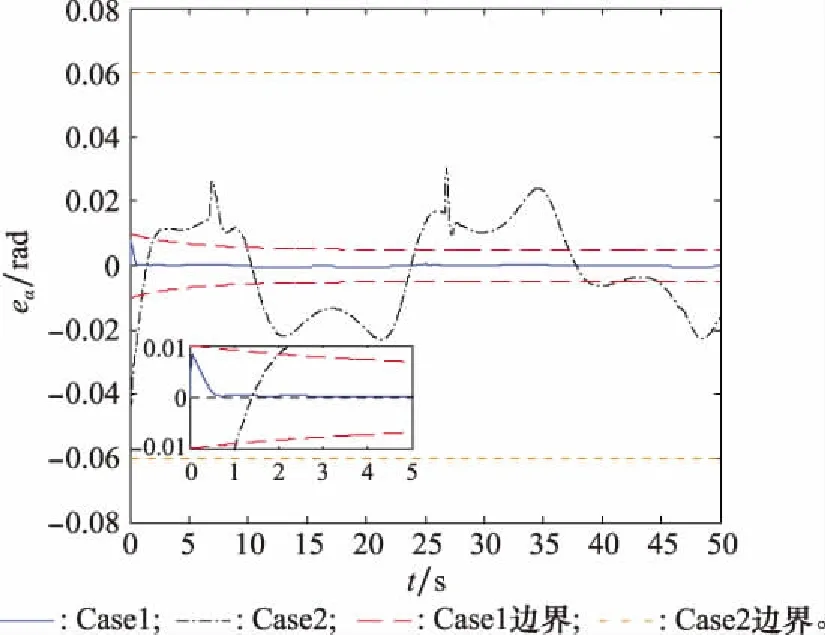
图4 攻角跟踪误差曲线Fig.4 Tracking error curves of angle of attack

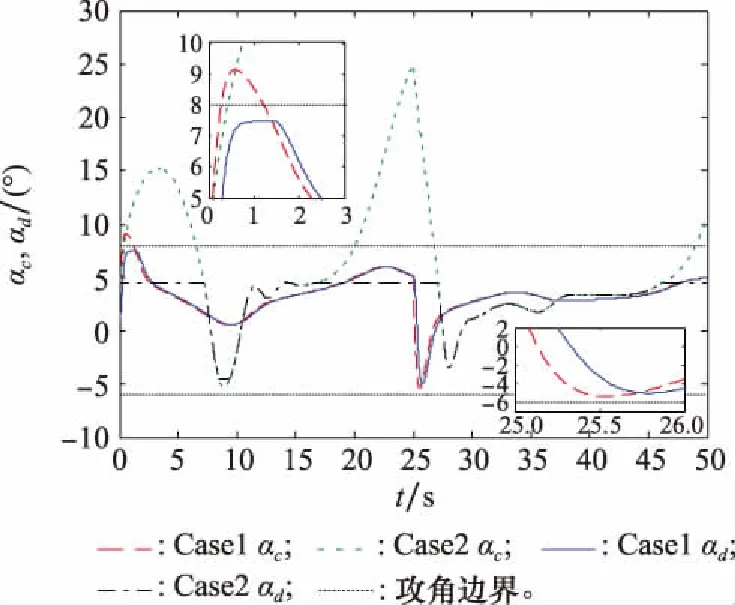
图5 攻角指令限幅曲线Fig.5 Limited curves of angle of attack command

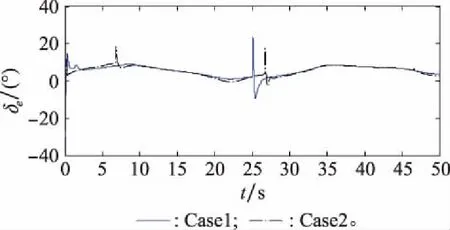
图6 控制输入曲线Fig.6 Curves of system input

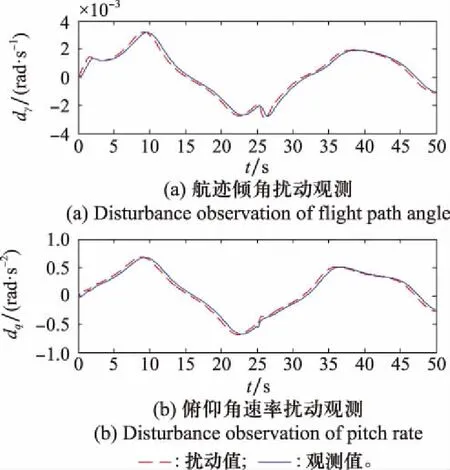
图7 LESO观测曲线Fig.7 Curves of LESO observation

5 结 论

针对考虑攻角约束的高超声速飞行器控制问题,本文提出一种受限指令滤波器与预设性能相结合的反演控制方案。该方案基于反演控制器设计,通过构造受限指令滤波器和采用预设性能方法,来分别约束攻角指令和跟踪误差,从而解决攻角约束问题,并从理论上完成了证明。最后通过仿真验证,该方案能够提供良好的跟踪性能,攻角始终满足约束条件,攻角跟踪误差满足预设的瞬态和稳态性能要求。