风险对冲策略复原传感数据的可行性分析

张 阔

（中国电子信息产业发展研究院，北京 100048）

技术风险是科研项目活动中普遍存在的[1]，因前期论证不充分、决策程序不科学、验收管理不规范等引起的一种高度不确定性，贯穿于技术设计、研发、应用全过程。特别是在技术研发阶段，若不重视全面风险管理工作，极可能导致技术创新不足、成果转化不力，使科研单位整体利益受损。

传感装置运动轨迹偏离预期路径，可能导致传感数据特征发生混乱，影响检测效果，这是传感系统应当关注的一种技术研发风险。当传感系统最大偏离程度远小于模型尺度时，传感数据对这种风险尤为敏感。本文以某声波—弹性波耦合模型为例，首先进行风险分析，研讨传感装置连同模型空间相对位置发生偏离对传感数据特征的影响，然后提出风险对冲策略，评估其对传感数据的最大复原程度，旨在对类似传感系统研发项目决策咨询工作提供理论指导。

1.模型概况

图1所示为声波—弹性波耦合模型在三维坐标系O－xyz下的设计图纸。在理想状况下，一无限长刚性柱体（一种非均质等效介质，本文忽视其内部结构的影响）位于无限长流体柱体正中心，轴心均为坐标轴Oz。流体柱体外包围一种无限大松软固体介质，传感装置的发射器（T）和接收器（R）均紧贴刚性柱体外壁。

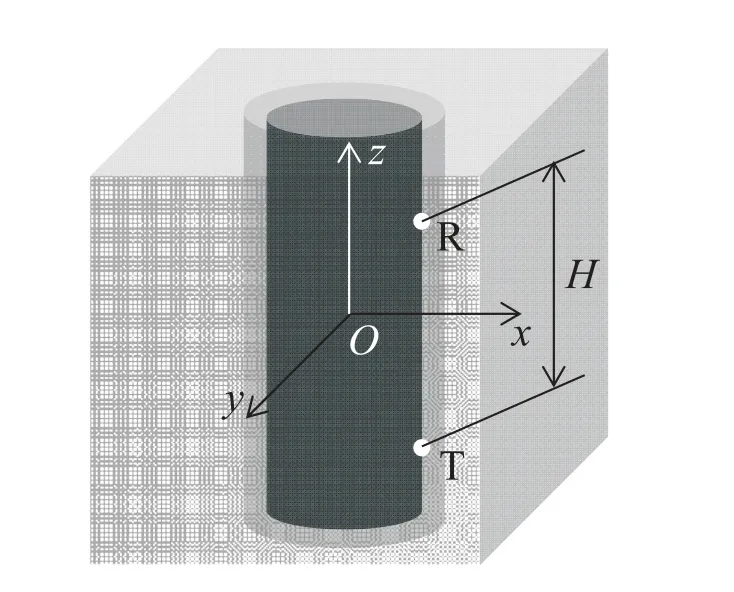
图1 三维设计图纸

1.1 相对尺度配置

为增强研究过程的普适性，不拘泥于模型实际尺寸，仅考虑相对尺度。假定同一方位下发射器与接收器之间的距离（H）为2个单位，同时，假定流体柱体主波波长(以下“主波波长”亦简称“波长”) 恰为1个单位。表1给出了模型其他规格、参数的相对尺度。一般地，模式波（若能被有效激发）更倾向于以波长小于2的介质所对应的波速占据传播主导地位。

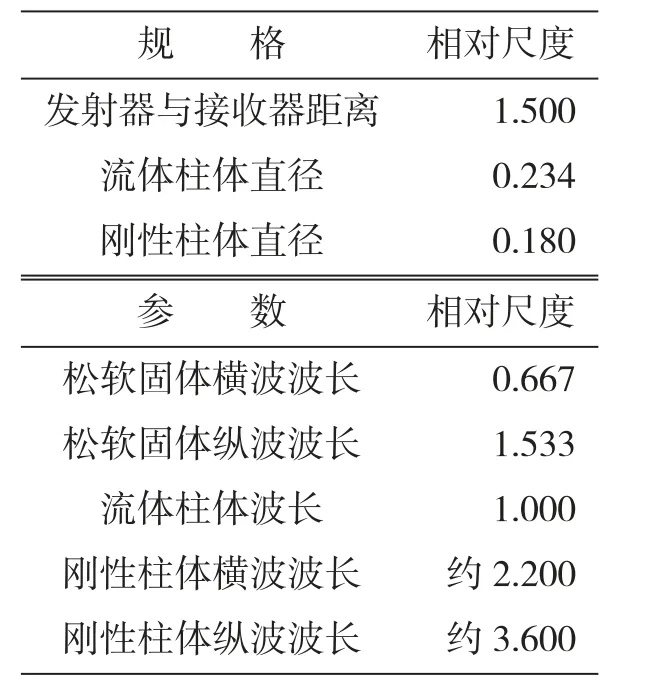
表1 模型其他规格、参数的相对尺度

1.2 传感装置设计

设计两种不同形式的发射器阵列，分别称作偶极阵列(下记“Di”)、四极阵列(下记“Quad”)，波源的周向布置方案分别如图2a、图2b所示。这两种阵列与经典的偶极子(n=1)、四极子(n=2)波源不同，其发射幅度在方位上并不严格满足与cosn的匹配关系，这将分别导致2m+1阶、4m+2阶(m>1且为整数)多极子模式被激发出来。当然，在本文设计的相对尺度下，上述风险能够得以规避，故出于成本效益考虑，这种阵列结构可以作为多极子波源的简化。文献[2]对这些问题进行了讨论，本文不再赘述。

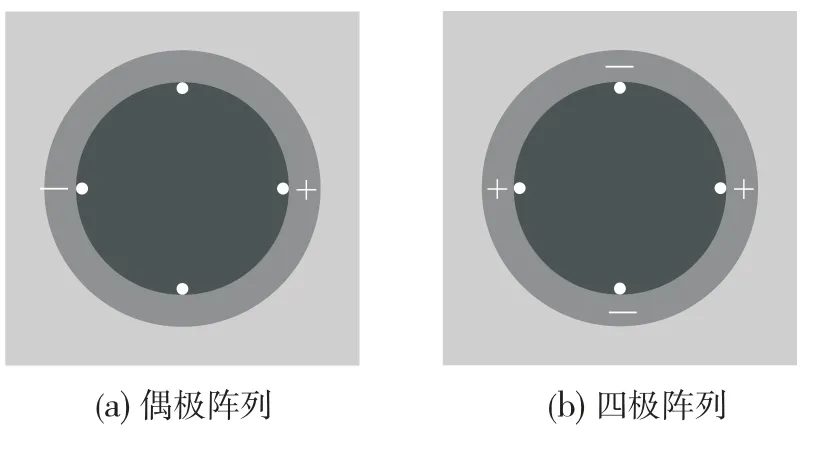
图2 发射器阵列波源的周向布置方案

接收器阵列的周向布置方案原则上与发射器阵列一致，但为了便于后续讨论，与偶极阵列相对应的接收器阵列也呈90°方位间隔布置。

1.3 传感系统偏离程度定义

图3所示为传感装置连同刚性柱体发生偏离的示意图。当刚性柱体轴心点由O偏离至O'时,根据表1,偏离矩|OO'|不会超过0.027，故定义偏离量Δx/X=|OO'|/0.027。同时,定义OO'与坐标轴Ox的夹角θ为偏离角。

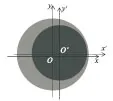
图3 传感系统偏离示意图

2.风险对冲方法与成效

将特定阵列结构、偏离角、偏离量下某方位接收器接收到的波形表示为Ssup(Ri,θ,Δx/X)。其中，上标sup可取di(代表偶极阵列)或Quad(代表四极阵列)；Ri代表序号为i的接收器，i可取1～4，分别代表0°、90°、180°、270°方位；θ和Δx/X的物理意义已在前文阐明。根据模型的几何对称性,对于Sdi，θ取0°～ 90°即可涵盖所有传感系统偏离情形;对于Squad，θ取0°～45°即可涵盖所有传感系统偏离情形。特别地，

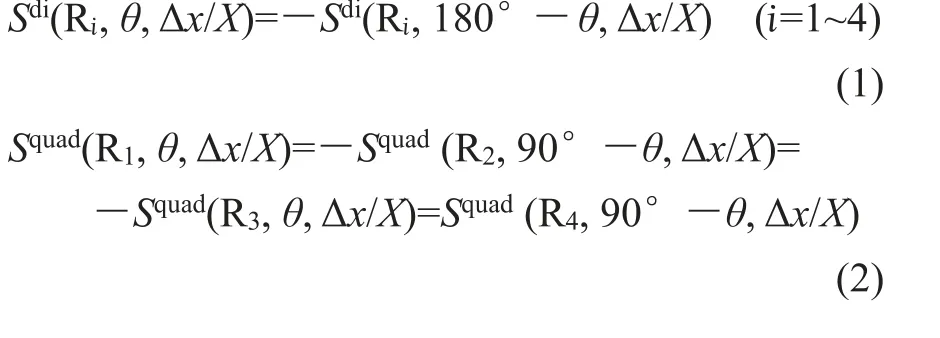
引入半整数维频域波动方程的有限元求解思想，将参数不变的z轴离散到波数kz域,构建2.5维声波—弹性波耦合方程的等效积分弱形式[3]，以期在较小求解成本、较高求解效率下揭示不同偏离角、偏离量对传感数据的影响。该求解方法已通过角频率—波数域[4]半解析测试。

2.1 偶极阵列

考察偏离角为0°、45°、90°,偏离量为1/3、2/3时的6种组合下，接收器R1～R4的波形曲线，如图4中第1～4道所示。其中，时间刻度与相对尺度的配置有关，本文不考虑其具体意义。为便于参照对比，图4中第0道一律列出偏离量为0时接收器R1的波形曲线，即偶极子模式（此时R3为R1的反向，R2和R4理论上为0）。

当偏离角为0°时，即使是微弱的偏离量，也使得R1与R3的反对称性大幅削弱，随着偏离量的继续增大，反对称性归于湮没；R2和R4的“零接收”特性受到了破坏，但二者保持对称性。当偏离角为90°时，无论偏离量如何，R1与R3的反对称性、R2和R4的“零接收”特性均可得以保持，且似乎看不出波形性态有什么异常变化。偏离角为45°的情形则比较复杂，因为以上提到的反对称性、对称性、“零接收”特性，轻者受到破坏，重者归于湮没，仿佛已没有数据复原的希望。

鉴于传感系统偏离对各方位的传感数据具有一定的对等补偿作用，根据各发射器/接收器的潜在贡献，提出以下适用于偶极阵列的数据对冲算式：

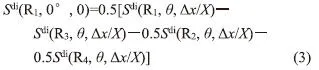
将式(3)应用于上述6种组合，并将计算结果覆盖于偏离量为0时的波形曲线进行对比，如图4中第0道标记的米字离散点。观察得知，当偏离量为1/3时，数据对冲算式在所有组合下均完美地复原了偶极子模式，就连偏离角为45°的极端情形也不例外。另一方面，当偏离量为2/3时，数据对冲算式不再适用，毕竟相位发生了严重畸变，已非简单的线性对冲所能胜任，即使在偏离角为90°的似乎较理想情形下也爱莫能助。总之，应被认作偶极阵列布置下主要技术风险源的是偏离量，而非偏离角。

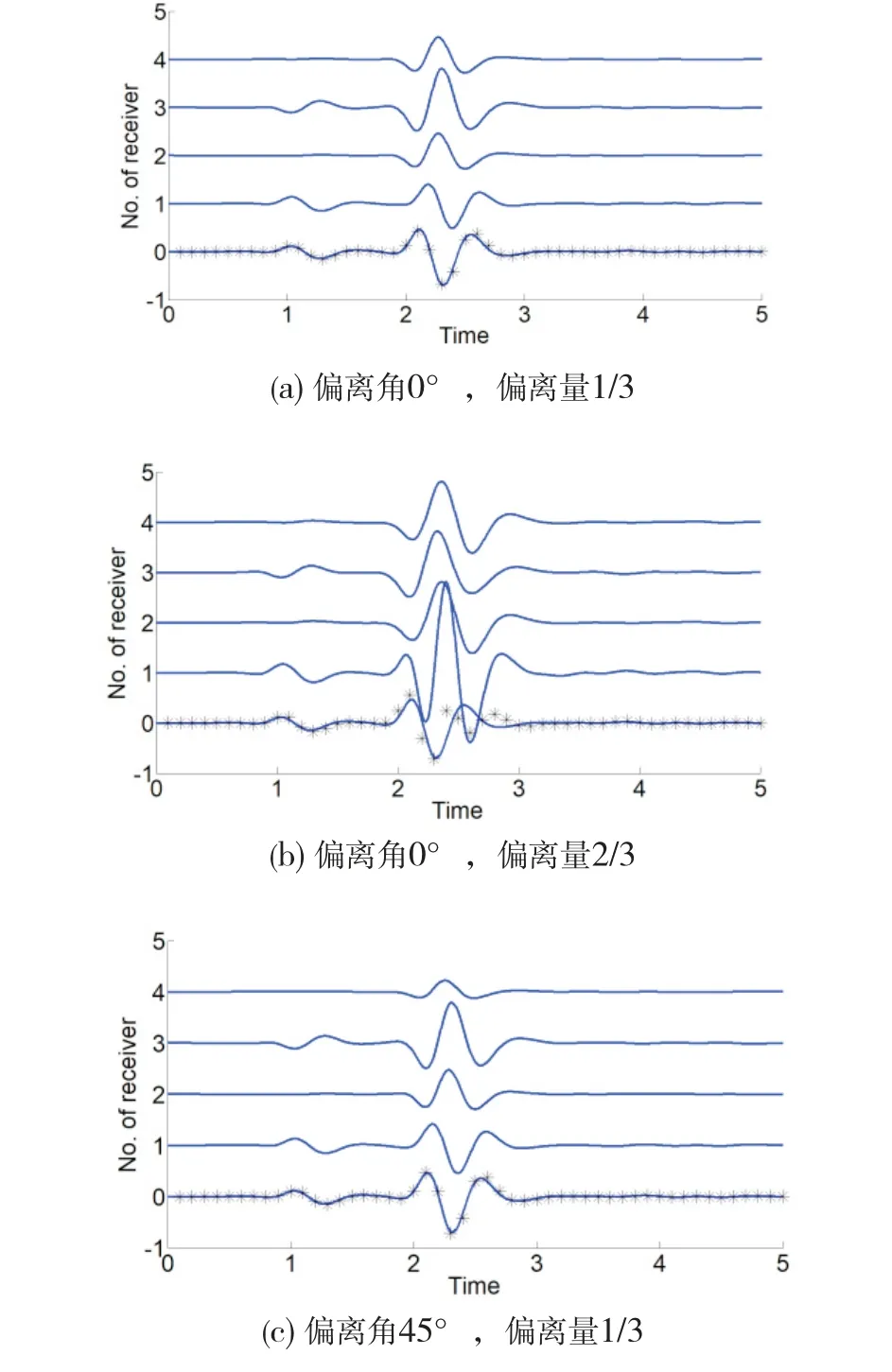
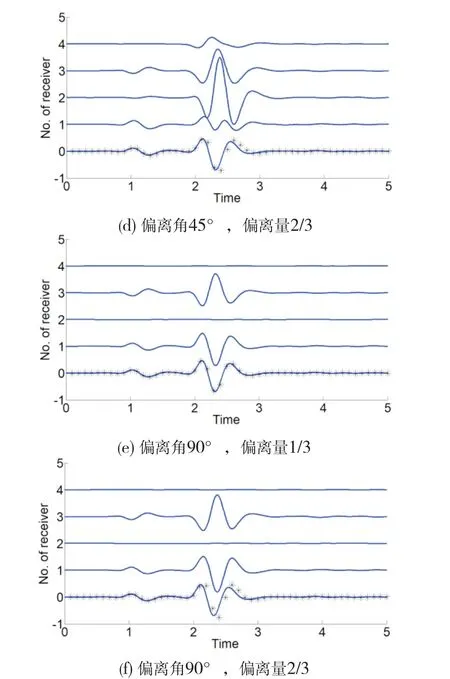
图4 偶极阵列波形

2.2 四极阵列

考察偏离角为0°、45°,偏离量为 1/3、2/3时的4种组合下，接收器R1～R4的波形曲线，如图 5中第1～4道所示。为便于参照对比，图 5中第 0道一律列出偏离量为 0时接收器 R1的波形曲线，即四极子模式（此时 R3与R1接收波形一致，R2与R4接收波形一致且为R1和R3的反向）。

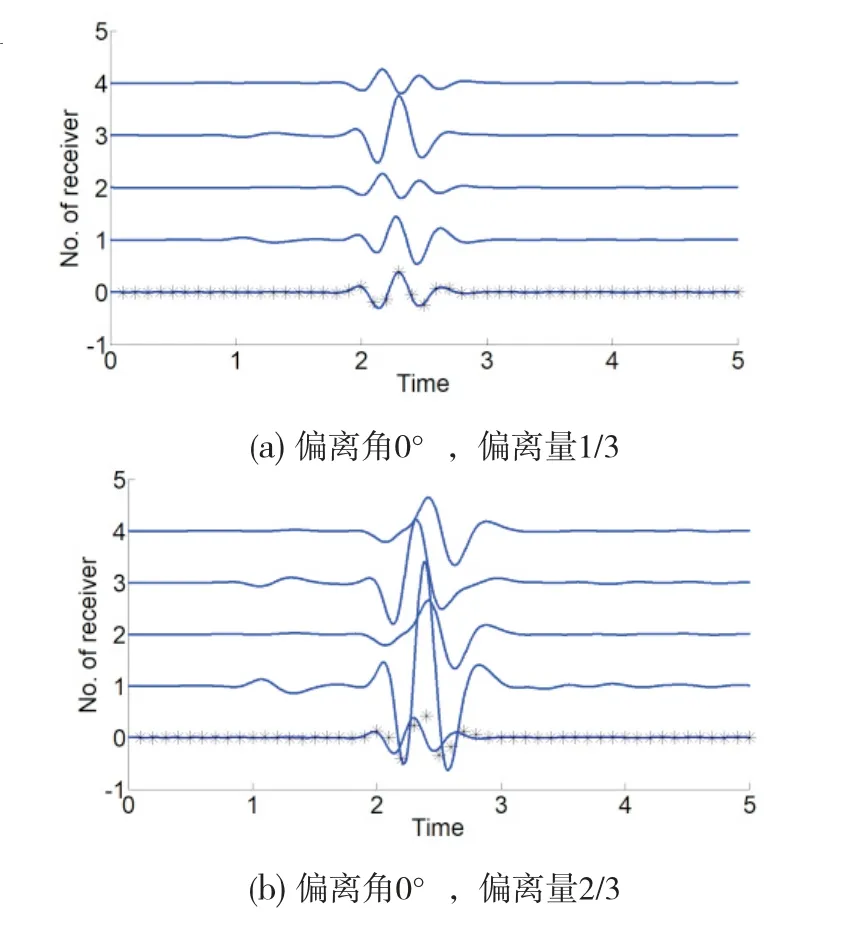
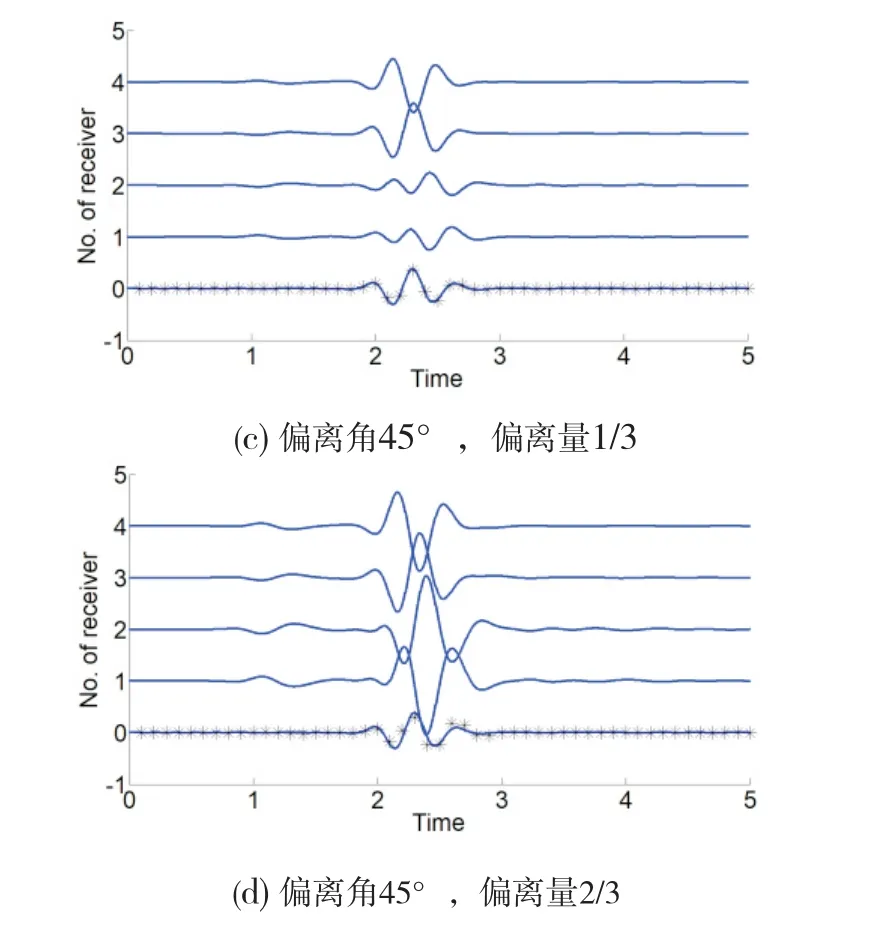
图5 四极阵列波形

如图5所示，当偏离角为0°时，即使是微弱的偏离量，也使得R1与R3的一致性明显削弱(能够肉眼观察到相位畸变)，随着偏离量的继续增大，R1与R3的一致性归于湮没，其中，R1或是由于受到了严重的空间挤压，竟迸发出超高的能量；根据模型的几何对称性，无论偏离量如何，R2与R4的一致性均可得以保持。当偏离角为45°时，无论偏离量如何，R1与R2的反对称性、R3与R4的反对称性均可得以保持，这也归功于四级阵列特殊的几何对称性结构。参照偶极阵列波形的分析思路，亦根据各发射器/接收器的潜在贡献，提出以下适用于四极阵列的数据对冲算式：

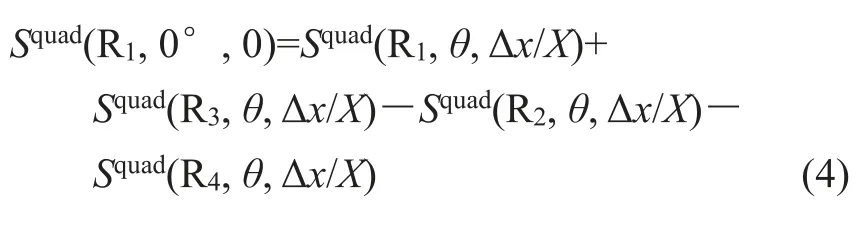
将式(4)应用于上述4种组合，并将计算结果覆盖于偏离量为0时的波形曲线进行对比，如图5中第0道标记的米字离散点。观察得知，当偏离量为1/3时，数据对冲算式在所有组合下均完美地复原了四极子模式。另一方面，当偏离量为2/3时，数据对冲算式不再适用，毕竟幅度、相位在不同情形下发生了不同程度的畸变，已非简单的线性对冲所能胜任。总之，与偶极阵列情形类似，应被认作四极阵列布置下主要技术风险源的也是偏离量，亦非偏离角。

3.分析

从第2部分的论述可知，无论发射器阵列是偶极阵列还是四极阵列，传感系统的主要技术风险源均是偏离量，即传感装置连同刚性柱体偏离初始轴心点的相对尺度。从这一视角来看，风险对冲策略在较大偏离量下似乎已成为不可行的解决方案。然而，第2部分的主旨仅在于从普适性的角度提出一种可能的数据复原算法，其仅是密切关注了传感数据形态的复原程度，却忽视了传感数据中蕴含的模式波在实际应用场景下的可用性。相比传感数据形态，部分行业对模式波的起跳时刻更加感兴趣，因为它才是判断模型中各介质实际波速的根本依据。况且，传感数据形态与波源函数、模型相对尺度等都是密切相关的，其不确定性是与生俱来的，属于不可控的系统风险。在本文设计的一系列规格、参数安排下，当偏离量为0时，偶极阵列激发的模式基本上仅包括偶极子模式，其又细分为1时刻前后起跳的刚性波和2时刻前后起跳的软性波（回顾图4中第0道）：刚性波的等效波速与模型中各介质的实际波速均难以匹配，它在业界是一种不受欢迎的模式波；软性波的等效波速与松软固体横波速度相匹配，往往成为关注焦点，但起跳更早的刚性波往往成为识别软性波的严重障碍。进一步回顾图4中第1～4道所示接收器R1～R4的波形曲线，发现当偏离角不为90°时，接收器R2和R4几乎接收不到刚性波，波形中仅存在幅度不一的软性波，这反倒成为提取软性波的等效波速，进而推测松软固体横波速度的有力证据，此时，风险对冲策略也似乎显得不那么重要了。

同理，在本文设计的一系列规格、参数安排下，当偏离量为0时，四极阵列激发的模式基本上仅包括四极子模式，其仅涉及2时刻前后起跳的软性波（回顾图5中第0道），即与松软固体横波速度相匹配的、往往成为关注焦点的模式波。进一步回顾图5中第1～4道所示接收器R1～R4的波形曲线，发现随着偏离角、偏离量的增大，这些接收器竟然接收到了近乎于偶极阵列激发的刚性波（其比文献[2]的“波源偏离”机理更为复杂），这反倒成为识别软性波的严重障碍，此时风险对冲策略成为必需。尽管偏离量较大时，数据对冲算式使得波形幅度、相位发生了失真，但刚性波的影响毕竟得以抵消。况且，万幸的是软性波的起跳时刻并未受到影响。

4.结语

技术风险是全面风险管理体系的重要组成部分，与其他风险一样，具有战略性、系统性。风险对冲策略是一种常见的风险管理工具，具有专业性、二重性。在使用风险对冲策略应对传感系统偏离这一技术风险进行传感数据复原时，既要充分发挥专业优势，善于运用职业判断，研判各发射器/接收器的潜在贡献，尽最大可能重现传感数据形态，也要综合考虑行业关注重点，在差异化的规格、参数安排下，充分评估传感数据的适用性、策略实施的必要性，更好地发挥技术研发项目决策咨询工作的创新引领、先行示范作用。