权期望填充准则作用下的Kriging自适应建模及全局优化算法

彭行坤，林成龙，马义中

(南京理工大学 经济管理学院，江苏 南京 210094)

0 引言

随着定制化产品等营销策略的出现，消费者个性化需求使产品设计和生产具备小批量、定制化的特点，传统实物试验设计已不能满足产品复杂程度高,更新速度快的系统设计要求[1]。基于计算机学科建模，数值计算和计算机软硬件技术发展而来的高精度仿真模型被广泛应用于产品和系统优化设计，有效提升了传统实物试验设计的质量和可靠度[2-3]。高精度仿真建模过程中的计算流体力学(Computational Fluid Dynamics, CFD)和计算固体力学(Computational Solid Mechanics, CSM)技术极大地减少了研发成本，但建模需耗费大量时间且因实际优化问题中往往无明确的函数关系，给工程建模和优化带来了极大困难[4-5]。近些年来，仅依靠初始样本就可近似模拟输入变量及响应变量二者之间函数关系的代理模型受到关注，先后产生了诸如响应面建模、KRIGING模型、径向基函数、支持向量回归及组合建模等代理模型[2,5]。上述模型因有效减少优化过程的计算量且具备较好的精度及稳健性在工程领域中得广泛应用[5-6]。其中，基于统计技术的Kriging代理模型因其能提供对未知试验点预测不确定性的度量且在小样本数据条件下具有高的预测精度受到众多科研工作者的青睐。

Kriging代理模型自1951年Krige博士提出以来，衍生出了梯度增强Kriging模型、Co Kriging模型、Blind Kriging模型等众多改进版本[7-8]，尤其在Jones等[9-10]基于统计假设提出最大化期望改进(Expected Improvement, EI)填充策略，对Kriging模型进行更新并寻找最优解的高效全局优化(Efficient Global Optimization，EGO)算法后，大大提升了Kriging模型在工程优化问题中的使用频率及求解效率[3,6-7]。其中，SCHONLAU等[10]引入参数来调整EI准则的区域探索能力，提出了适用于包含黑箱约束问题的处理方法；ZHAN等[11]提出了通过设定阈值来调整和改进EI探索能力的并行EGO算法；SUPRAYITNO等[12]提出的可靠域Kriging代理进化优化(Evolutionary Optimization using Reliable regional Kriging Surrogate, EORKS)算法，通过混合填充策略防止过早局部收敛。此外，基于代理模型化产生了诸多有代表性的优化算法，例如基于置信下线准则(Lower Confidence Boundary, LCB)、可行性概率(Probability of Feasibility, PoF)准则的众多算法[7,13-14]。随着工程研究对象的复杂化，在计算机试验建模技术的快速发展推动下，基于Kriging模型的代理优化算法已成为解决高度非线性，且具备昂贵仿真黑盒模型特点问题的重要解决方案之一[6,13]。

计算机试验建模过程中发现，EI填充准则新增试验样本点具有较好的全局探索能力，有效地改善了Kriging模型预测精度及建模效率[2,11]。在EI准则及PoF准则的基础上产生了诸多填充准则，如张建侠等[15]提出了多目标策略和聚类分析的代理优化算法，并将其应用于压力容器的优化设计中;JIAO等[16]在约束条件辅助下提出的约束完备EI准则，在探索当前可行区域的同时，还可开发不可行但有发展前途的区域；SUN等[17]通过Pareto前沿点集实现多点选取，改善新样本点探索可能性的同时提出了并行多目标优化算法；CINQUEGRANA等[18]通过给定逐步下降的权值来调整EI的探索能力，并将其应用于翼型优化设计中。张鹏等[19]依据复相关系数R2实现Kriging模型的自适应设计，并将其应用于注塑机模板应力、变形测试及优化。研究发现，上述准则多集中于PoF准则，改变可靠性程度或者提升可行性区间的变化，鲜少有文献以EI新增试验点作为参考点，从而减少EI准则贪婪特性导致的陷入局部优化问题[20]。因此，研究具有距离特点的权函数来建立新的期望填充准则显然是一种大胆尝试，但就目前研究来看尚有欠缺及不足[21-22]。

本文对EI准则进行修改，提出两种基于参考点的权期望调整准则，并将其与代理优化算法相结合，综合运用Kriging建模技术及进化算法实现对包含约束条件的优化问题进行求解，提出了基于权期望填充准则的全局优化算法。该算法通过具有距离特性的权函数实现对EI填充准则新增试验点进行调整，使其在具备平衡全局探索和局部探索能力的同时，可以使新增样本点具备距离特性，以提升建模效率及模型预测精度。最后，通过数值试验算例及工程实例进行比较分析，验证了所提权期望填充准则作用下的全局优化算法的有效性。

1 权期望加点准则作用下的全局优化算法

受制于工况、机械性能等因素，工程中的全局优化问题一般均具有约束条件，其可用一般意义上的数学公式进行表示，具体形式如下：

minf(x);

s.t.

gi(x)≤0,i=1,2,…,r,

x∈D。

(1)

其中：f(x)是目标函数；r为整数，指共具有r个约束；gi(x)表示第i个约束条件；x∈D⊆Rd表示d维设计变量；D=[xl,xr]表示变量的矢量矩阵，xl,xr分别表示变量的左、右边界。

1.1 Kriging代理模型

假定样本集Ω中包含m个试验点，定义样本观测变量矩阵为X=[x1,x2,…,xm]T,其对应的响应值矩阵为Y=[y1,y2,…,ym]T,Kriging代理模型可表示为：

y(x)=μ+z(x)。

(2)

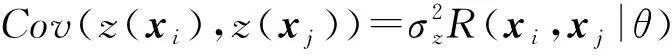
(3)

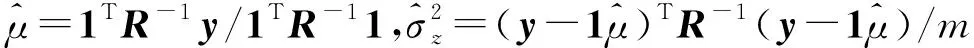
Kriging模型中的相关函数通常选择常用的核函数,如高斯函数、样条函数、Matérn函数等。具体可参考文献[2-3]。

1.2 权期望填充准则

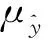
(4)

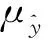
EI(x)=EI1+EI2,

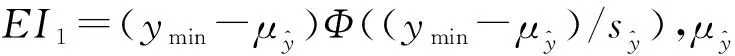
为了平衡全局和局部探索能力，一般会对EI1和EI2分别赋予不同的权重，对两者进行简单的加权或采用熵权准则来依据EI1和EI2的重要程度确定权重[18]，将EI函数修改为如下格式：

EI(x)=w1EI1+w2EI2。

式中w1,w2∈R，且w1+w2=1。

xR=argmaxEI(x)。

ZHAN等[21-22]在研究多点填充准则时提出了影响力函数(Influence Function，IF)，来调整和近似EI改进函数，称为伪期望改进(Pseudo Expected Improvement, PEI)准则，其本质思想是构造权函数(Weighted Function, WF)。以经典的高斯相关核函数为例，权函数表达形式如下：

权函数满足权的一般性质且具备距离特性，同时这也是具有空间距离特性相关函数对于Kriging模型特有的校正和平滑功能，但上述PEI准则仅被用于并行填充设计，未进行单个加点尝试。为了避免EI准则过于贪婪而陷入局部最优，通过权函数对其进行调整的同时设定变量维度d的倒数作为幂指数来减缓其收敛速度。基于上述考虑，将权函数分别应用于EI函数的不同位置，获得两种新的权期望填充准则，其表现形式如下：

和

其中d为设计变量维数。

1.3 可行性概率准则及约束处理方法

EI填充准则是为解决无约束优化问题设计的，对于具有复杂非线性黑箱约束的工程优化问题，考虑新增试验点在约束范围内的可行性概率准则非常适用[10]。

现有文献大多将PoF作为EI准则权重的约束应对方法应用在实际问题中，即以PoF为权重的约束期望改进(Constrained Expected Improvement, CEI)[2,10]，可表示为：

CEI(x)=E(1gi(x)≤0·I(x))=EI(x)·PoF(x)。

同理，依据新的填充准则可获得约束条件下的权期望改进准则：

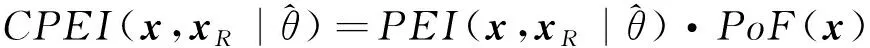
约束权期望准则伪实现代码如下：

步骤1计算满足最大期望约束条件的参考点xR：

步骤2计算新增试验样本点x：

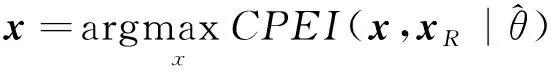
1.4 EGO算法及其实现流程

EGO算法一般是指利用少量初始样本构建初始Kriging模型，采用最大化期望改进填充准则选取增加新试验点进行样本填充设计，通过更新迭代过程不断自适应修正模型，直至满足终止条件获取最优解的算法实现过程。其算法流程图1所示。

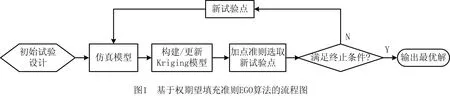
上述流程实现具体伪代码如下：

步骤1最大最小拉丁抽取5d+1个观测点，获取样本集(X,y)和约束矩阵G=[g1,g2,…,gr]T,设定终止条件,获得初始最优可行解ymin(x)。

步骤2While终止条件不满足do

依据(X,y)建立目标函数初始Kriging模型

fori=1 tor

依据(X,G)构建约束初始Kriging模型

end for

步骤3判断gi(x)≤0,样本集是否有可行解。

if无可行解,then采用可行性概率准则增加可行试验点，

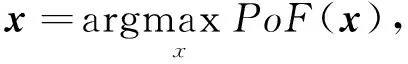
else

end

步骤4更新样本点x,y(x),gi(x)，更新样本集

X=X∪x,y=y∪y(x),

G=G∪[g1,g2,…,gr]T。

步骤5更新当前最优可行解ymin(x)

end while

2 测试算例与分析

2.1 数值算例

为了更好地说明新提加点准则的有效性，选取分别包含5个和10个变量的G4、G7数学测试函数[23]，以及包含7个变量的减速器设计(Speed reduce design, SRD)案例[24]、11个变量的汽车侧面碰撞(Car Side Impact, CSI)案例[25]、进行试验验证，并将结果与经典EI准则进行对比，验证所提算法的有效性、高效性和稳健性,算例具体信息如表1所示。

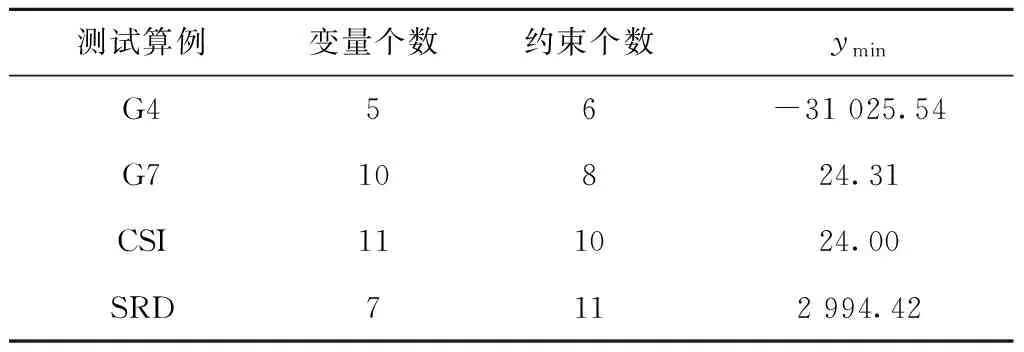
表1 算例相关信息

2.2 优化结果与分析

所有测试均在MATLAB 2017a，Think Pad环境下运行；为保证结构稳定性，采用最大最小拉丁设计抽取5d+1个样本作为输入样本矩阵X，仿真获取相应的响应矩阵Y及约束矩阵G。为方便分析，本文以仿真试验的总次数T作为优化算法的终止条件，当T=100时，算法停止，并返回最优解。

(1)算法收敛图

首先比较各加点准则下算法的收敛效果，为消除初始试验设计随机性对优化结果的影响，用30组初始试验设计下优化结果的平均值随迭代次数变化的曲线来评估各算法的寻优能力和收敛性。3种加点方法的收敛效果如图2所示。

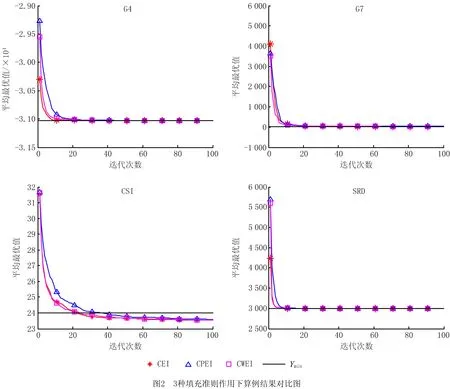
如图2所示，迭代次数越少，结果越接近已知最优值，则表明该准则下的算法收敛速度更快；最终解接近或小于已知最优值则表明该准则下的算法精度更好。从图2可以看出，4个算例在3种加点准则的作用下随着迭代次数的增加均可收敛至近似最优解，说明了两种新权期望填充准则作用下的代理优化算法的有效性。对于G7、CSI和SRD算例，在到达相同精度的情况下，CWEI准则相较于EI准则的迭代次数更少，说明CWEI准则作用下的优化算法是加快收敛速度的有效方法，而对于CPEI准则，其收敛速度虽然相较于经典EI准则和CWEI准则更慢，但其近似最优解具有更好的精度。对于G4算例，虽然CPEI和CWEI准则收敛速度相较于EI准则更慢，但整体差距并不是很大，且能够很好地收敛到近似最优解。

(2)算法性能表

表2 不同优化算法结果比较

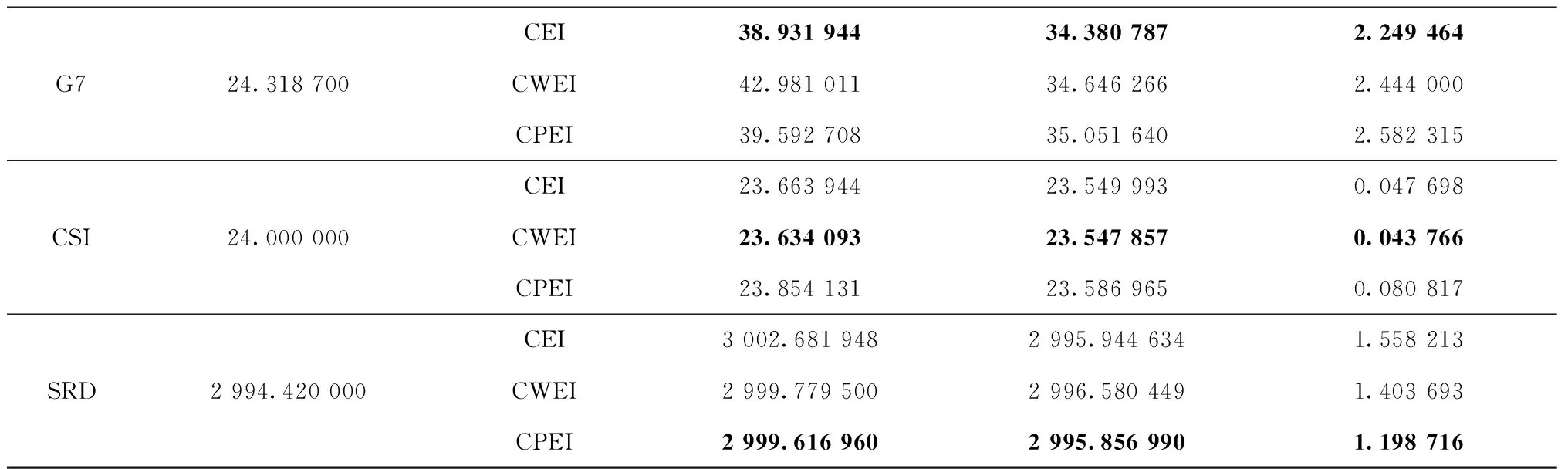
续表2

对于G4和SRD算例，CPEI准则的最大值、平均值和标准差都优于EI准则，说明CPEI准则作用下的优化算法能够更好地对最优解区域进行探索，且该准则受初始试验设计随机性的影响最小；而CWEI准则在标准差方面优于EI准则，虽然最大值和平均值没有比EI准则更优，但是其结果接近已知最优值，说明该准则是有效的。对于CSI算例，CWEI准则的结果更好，CPEI准则也具有较好的表现。对于G7算例，虽然EI准则的结果更优，但CWEI和CPEI准则的平均值相较于EI准则差距并不大，说明两种准则作用下的优化算法也具有较好的精度。总体来说，新提两种加点准则具有较好的有效性和寻优稳健性。

(3)算法箱线图

对于每个算例中每种算法的30次结果，绘制结果的箱线图，纵坐标是30次结果的近似最优值，结果如图3所示。

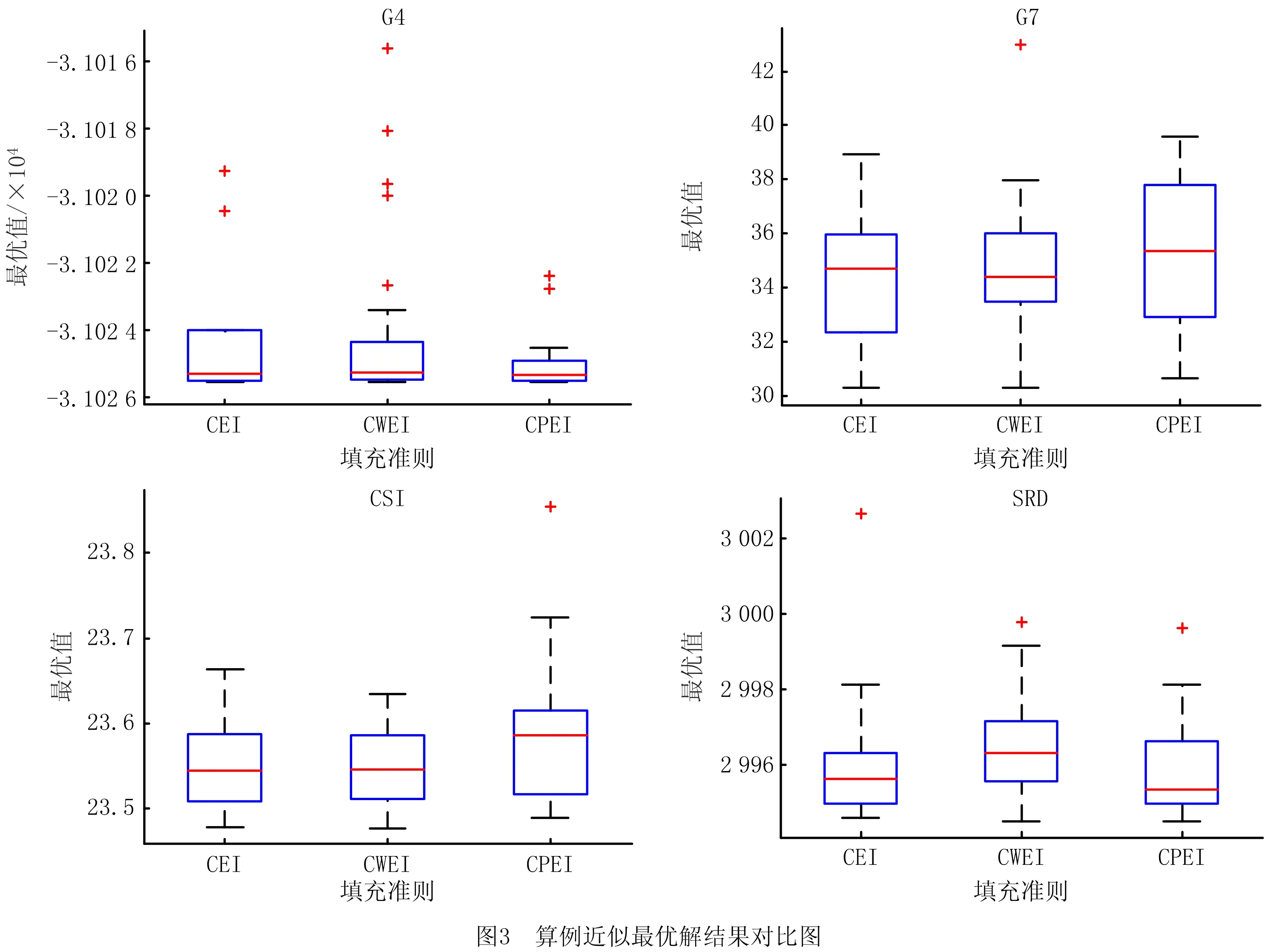
对于G4算例，CWEI和CPEI准则的结果均比EI准则的结果更加集中，说明两种准则受实验随机性影响较小，对于G7、CSI和SRD算例，CWEI和CPEI准则的结果均和EI准则的结果相近，且波动范围不大。总体来说，CWEI准则及CPEI准则均可获得较好的近似最优解，且稳健性较好。

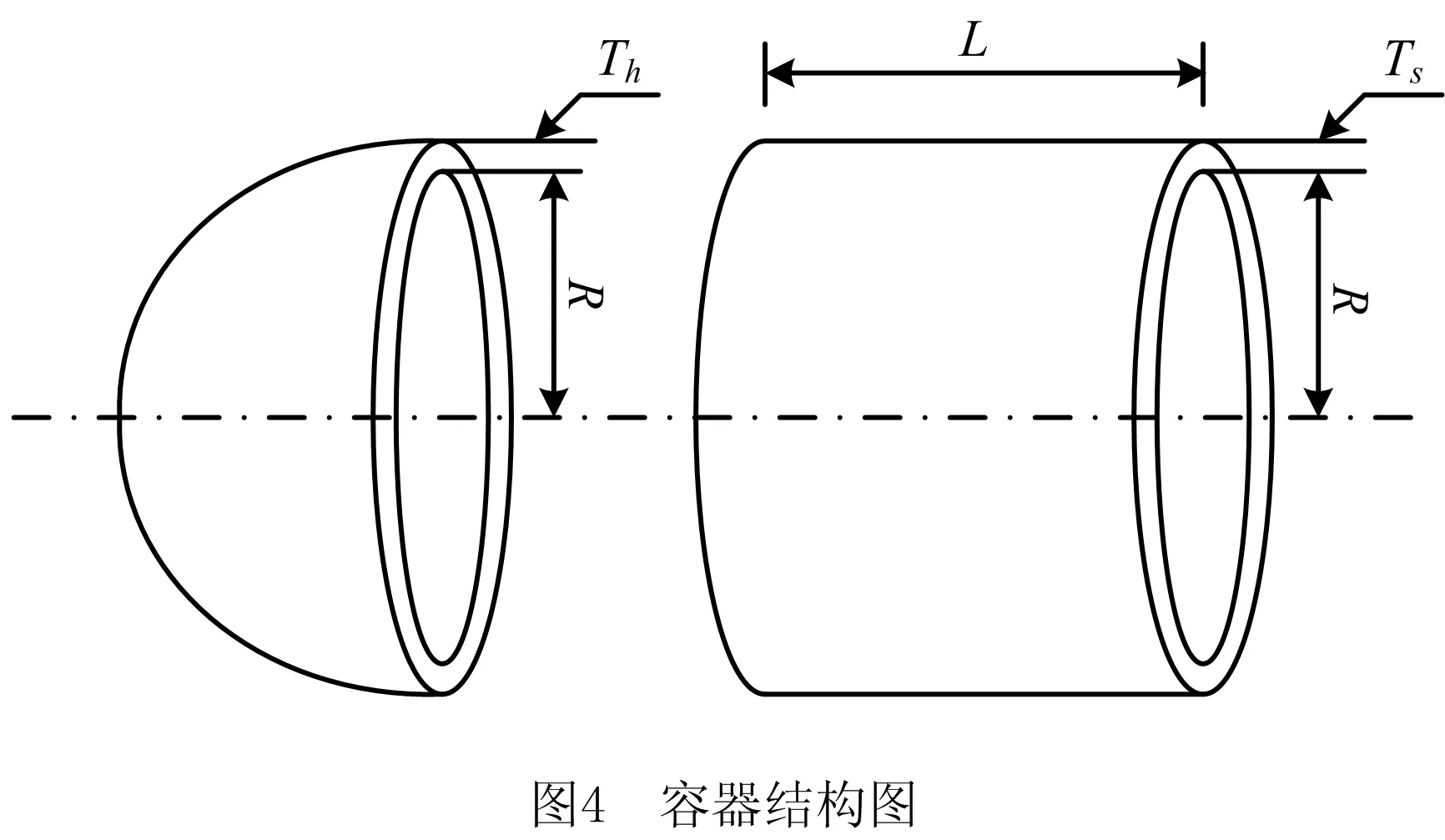
2.3 工程实例

该实例是一个圆柱形容器设计，由圆柱体和半球体组成，结构如图4所示。该实例有4个设计变量：Ts(圆柱体壳厚度)、Th(半球体厚度)、R(内半径)和L(容器的圆柱形部分的长度)；优化目的是使总成本降到最低；包括材料，成型和焊接的成本。工程实例的数学模型如下：

minf(x)=0.622 4TsRL+1.778 1ThR2+

s.t.

g1(x)=-TS+0.019 3R≤0;g2(x)=-Th+0.009 54R≤0;

g4(x)=L-240≤0,

0.062 5≤Ts,Th≤0.062 5×99,10≤R,L≤200。

运用本文提出的CWEI和CPEI准则，对此工程案例进行求解，并与EI准则以及其他文献中的结果进行对比，如表3所示。对比结果发现，近似解接近最优值，说明了新提两种加点准则的有效性，且两种准则作用下的算法能够很好地解决文献中的实际工程问题。

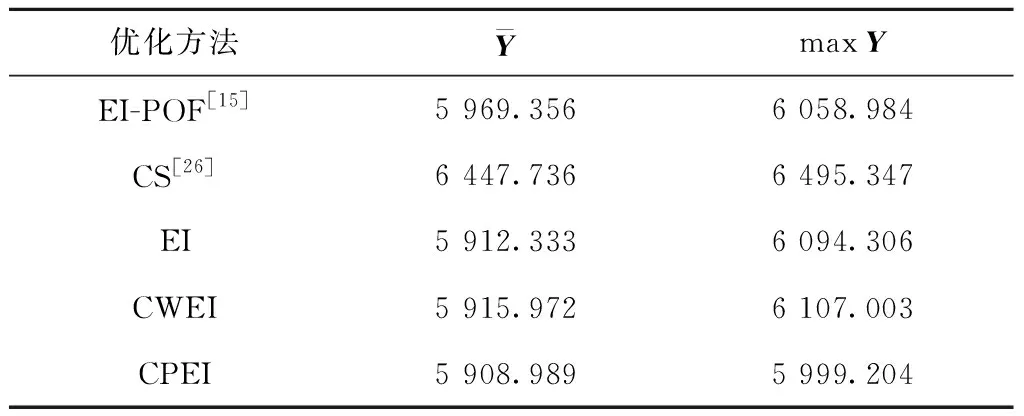
表3 结果对比表

3 结束语

算例试验以及工程实例结果表明，基于Kriging代理优化模型和两种权期望填充准则的EGO算法可有效地处理和优化复杂的黑箱过程。本文基于经典EI准则和Kriging模型预测不确定性提出的两种权期望填充准则具有良好的空间探索能力，所提两种新EGO算法在解决单目标约束优化问题时有效，且在算法的可行性、建模效率和解的稳健性方面具有一定优势。具体结论如下：①3种填充准则作用下的EGO算法均可快速地收敛到近似最优解，但从收敛速度来看,CWEI和CPEI准则略优于EI准则；②3种填充准则作用下，CWEI准则受试验随机性影响最小，稳健性最好，可有效减少试验次数；③相同条件下，CPEI和CWEI准则相比EI准则近似最优解的标准差更小，解的质量更高；④两种新的加点准则，只需要较少的试验就能求得优化问题的最优解，是提高工程优化设计效率和质量的有效途径。

试验结果表明,通过权函数可有效调整EI准则的全局和局部探索能力，注意到3种不同的填充准则可实现不同位置的加点，故3种填充方法也可实现多点同时加点。未来，实现现有准则基础上的一次多点加点是可以研究的领域；将该方法应用到解决多目标优化问题也是未来研究的方向之一。