基于累积成本限制的k-out-of-n:F系统维护决策
2022-04-04周宏明罗晓璇黄华浙綦法群黄沈权
周宏明,罗晓璇,黄华浙,张 宁,綦法群,2+,黄沈权
(1.温州大学 机电工程学院,浙江 温州 325035;2.同济大学 机械与能源工程学院,上海 201804)
0 引言
在实际生产中,对系统采用冗余设计是提高系统可靠性的有效方法。常见的系统冗余方式一般有k-out-of-n:F系统、并联、贮备等形式,其中k-out-of-n:F系统在工业界和学术界都得到了广泛关注。
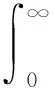
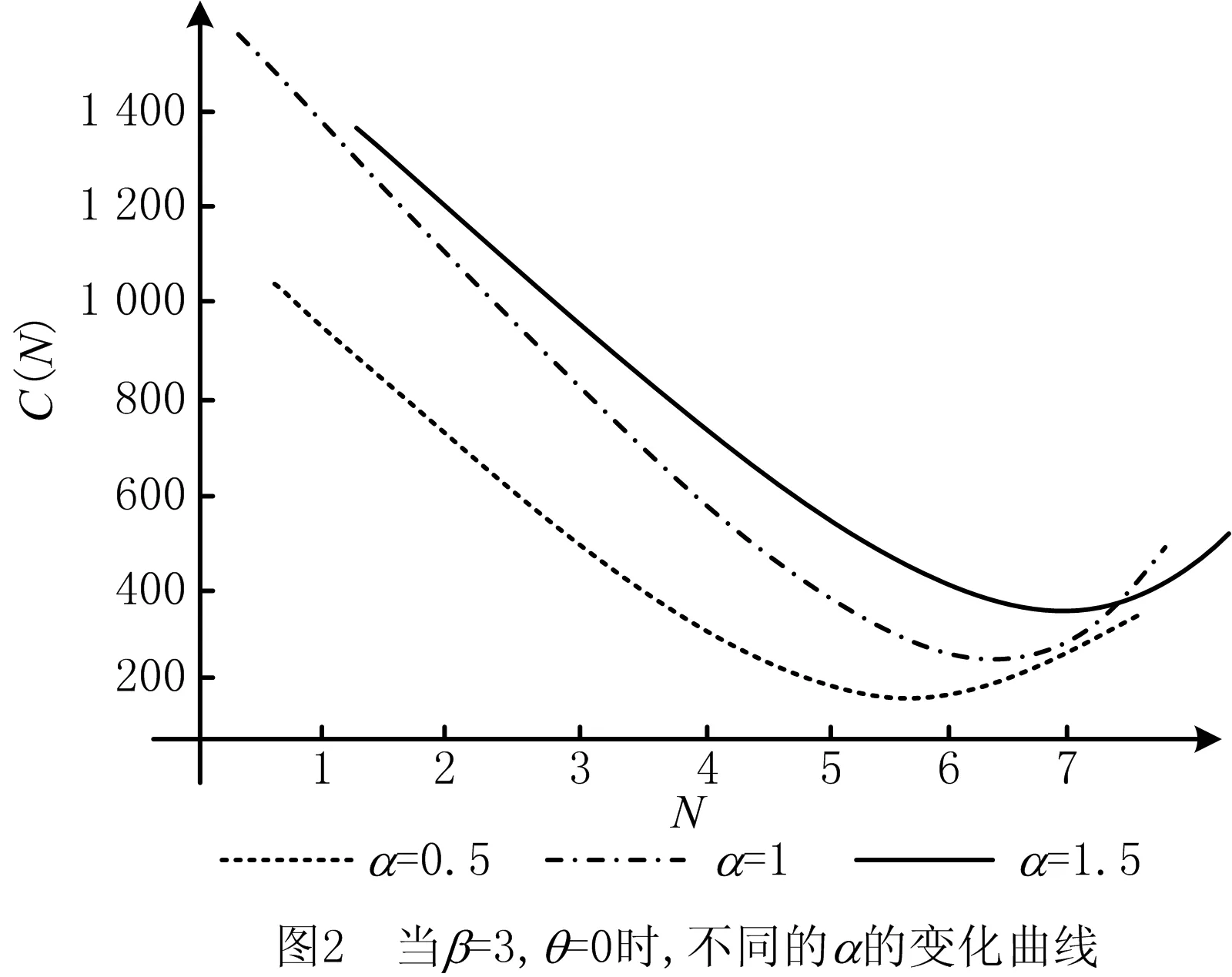
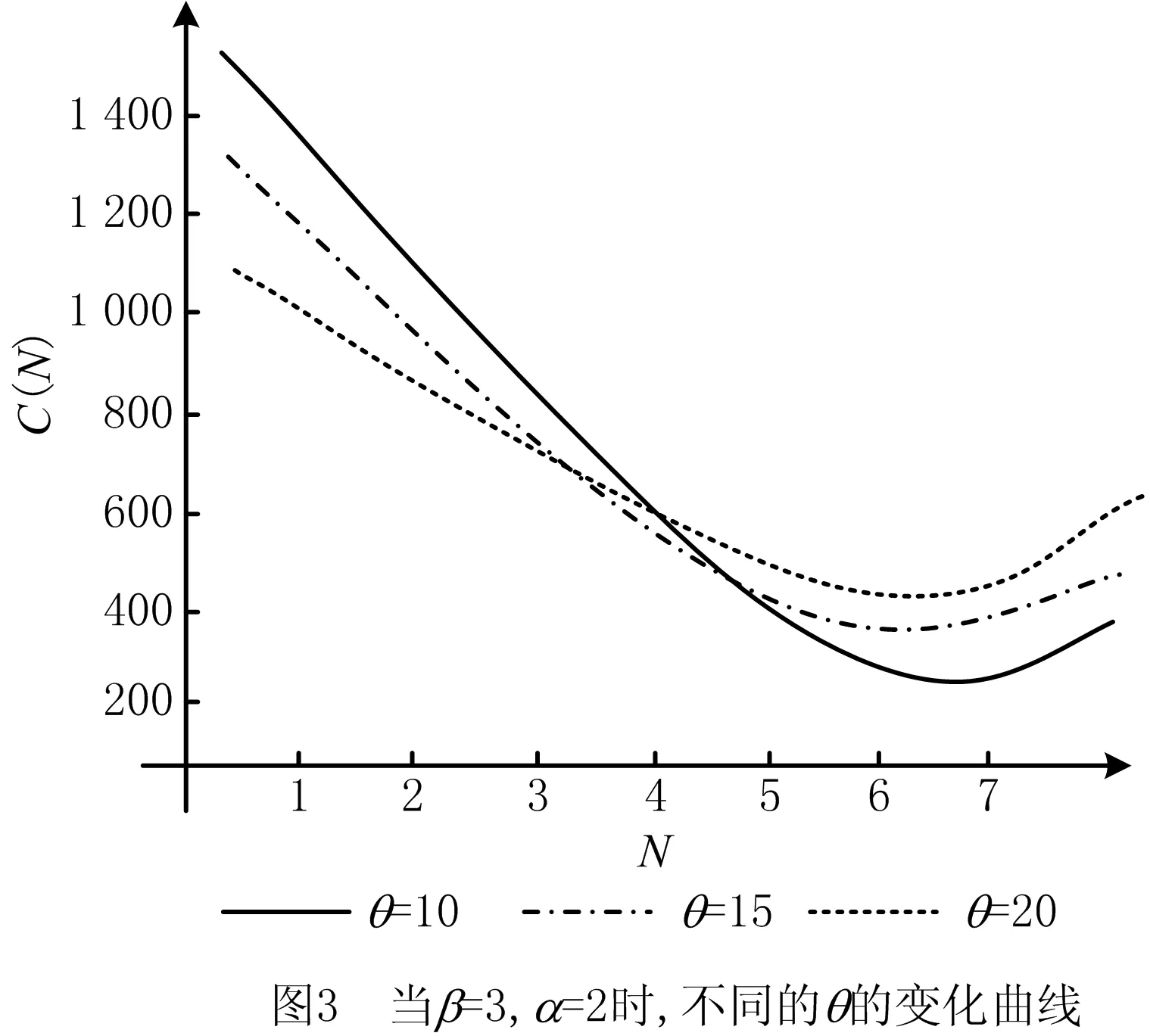
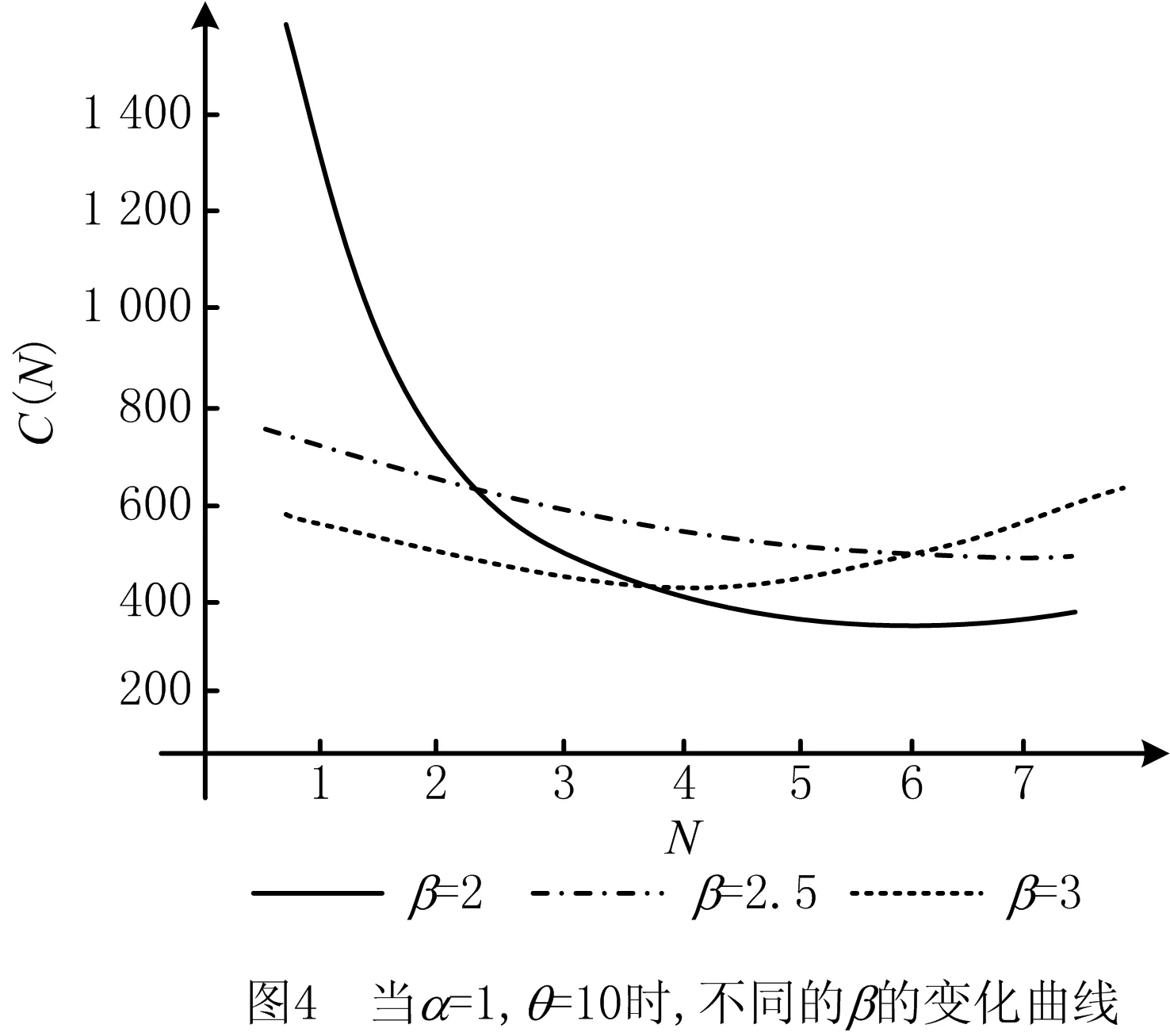
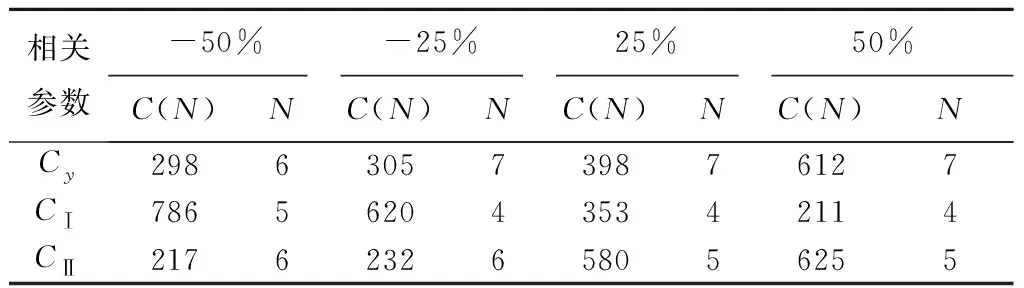
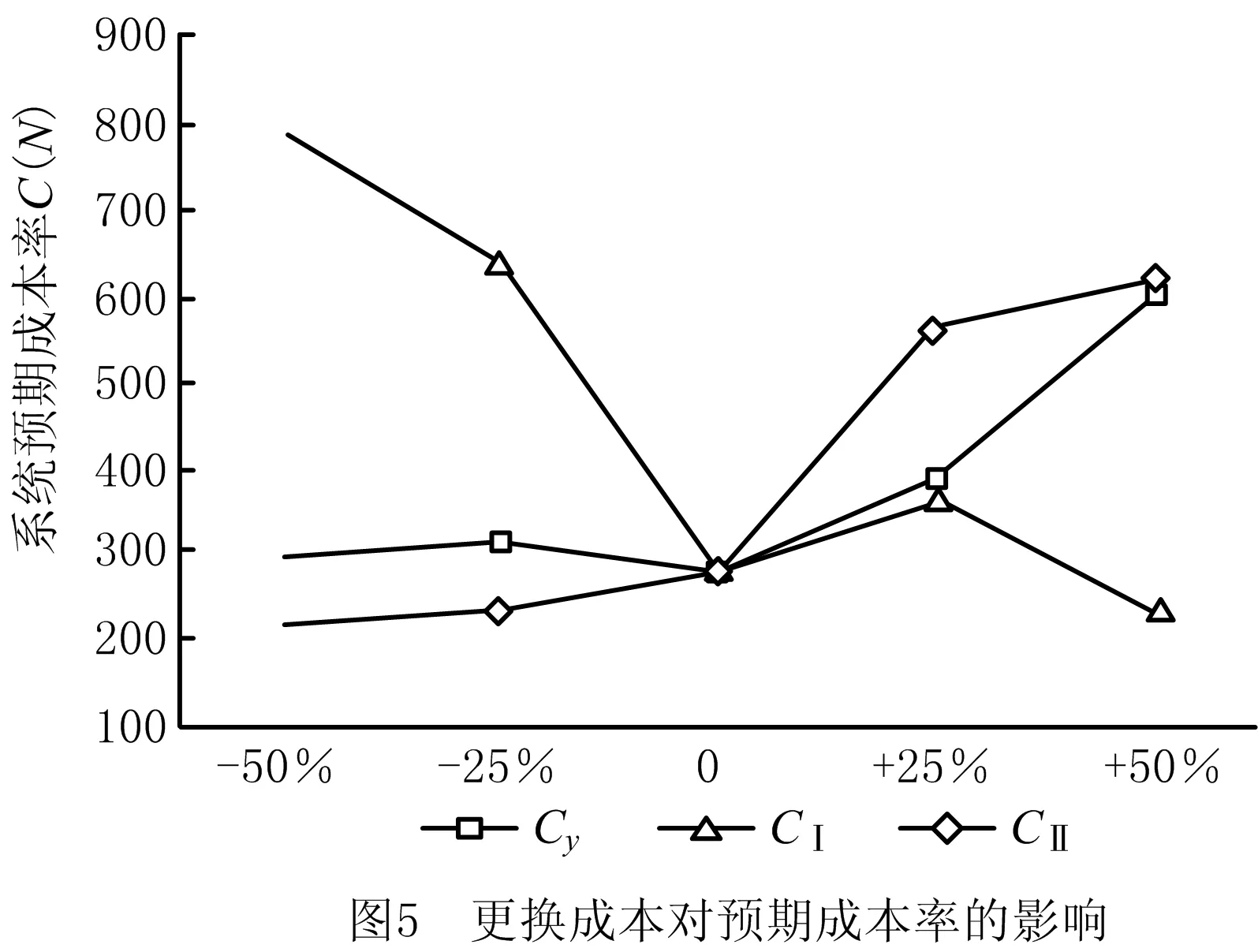
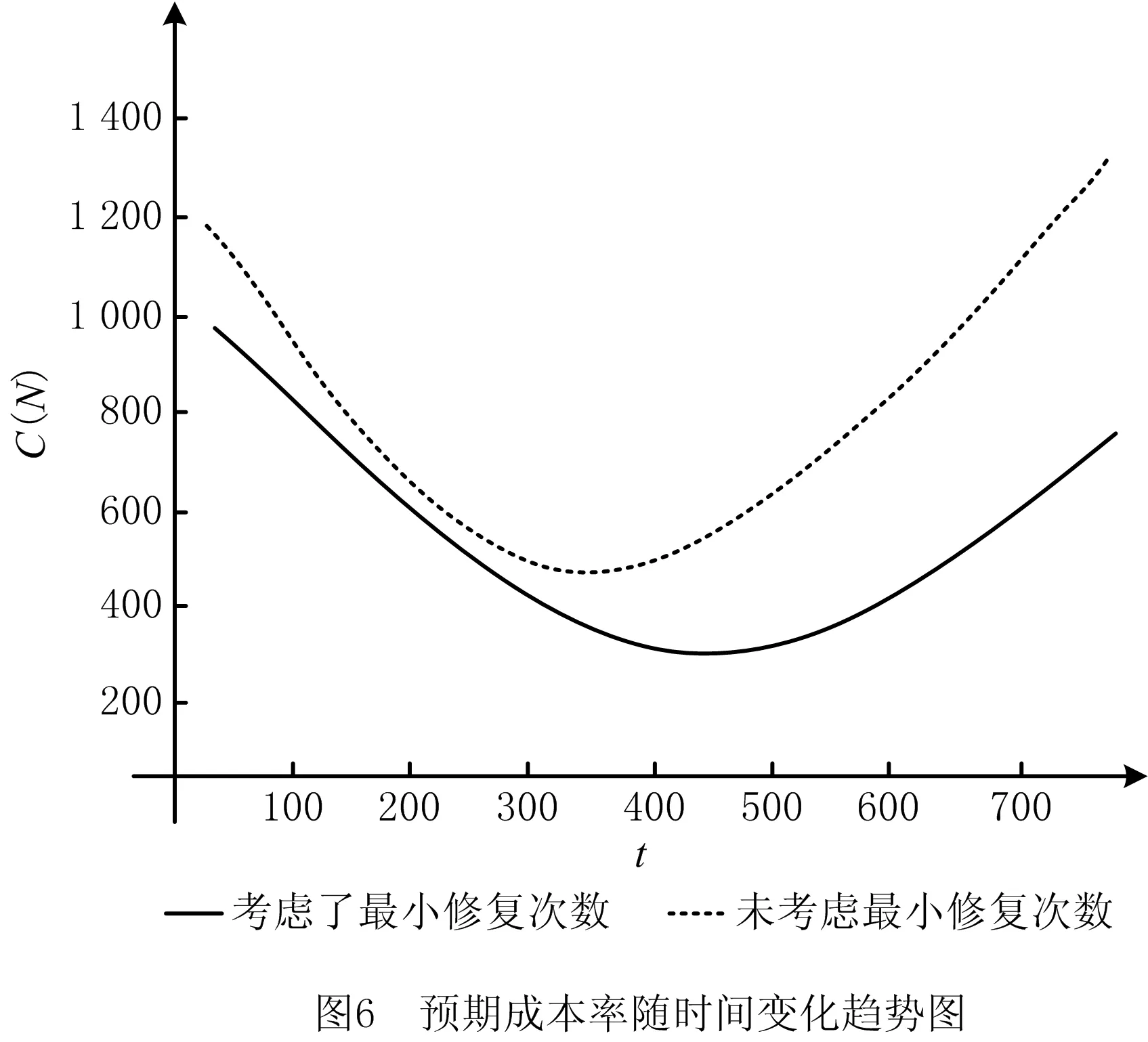
SHEU等[1]研究了k-out-of-n:F系统,该系统在运行过程中会受到外在冲击。当系统的役龄达到T(T>0)时,对它进行预期更换;若在预期更换时间点之前,由于外部冲击导致系统失效的部件数量j 上述针对k-out-of-n:F系统的维护决策大多只关注单次维护成本,且往往只对维护周期进行优化研究。在这种维护策略下,系统在其生命周期内的累积修复成本往往极高。为此,国内外许多学者提出了基于资源约束的维护策略。潘尔顺等[11]将成本与设备利用率进行有机结合,建立了动态维护时间模型,对系统进行了动态维护策略研究。张博文等[12]以系统的生产和维护总成本最小化为目标构建了生产计划和预防性维护联合决策的模型。方珍玲等[13]基于设备的维护效率对系统进行了预防性维护优化研究。邵建一等[14]提出一种基于产能约束资源的设备预防性机会维护建模方法,在分析设备可用性和维护成本的基础上,对系统不同种类设备进行了预防性维护建模。张友鹏等[15]提出了一个针对单设备的动态预防性维护模型,该模型是在有限时间内基于可靠度的约束,建立考虑役龄回退因子以及故障率递增因子的故障率函数来描述设备的退化过程。以设备的最低工作可靠度为限制,使得更换周期内系统的总维修费用率最小,并确定系统的最优预防性维护次数和维护周期。BEICHELT[16]提出了基于维修成本率限制的替换策略,即一旦维修成本率超过阈值水平,系统就会被替换。CHANG等[17]研究了单部件系统基于累积成本限制的更换策略。但是上述基于累积成本限制维护模型的研究对象大都为单机系统。对k-out-of-n:F系统来说,部件间往往存在失效相关性,系统中失效部件的数量又与系统性能密切相关,系统呈现多种失效形式。基于此,本文以k-out-of-n:F系统为研究对象,考虑系统部件之间的失效相关性,根据系统中失效部件的数量将系统故障分为两类,建立以累积修复成本率最小为目标的维护决策模型,并采用迭代算法求解最佳维护决策。 k-out-of-n:F系统由n个独立部件构成,当且仅当至少有k(1≤k≤n)个部件故障时,系统失效。m为系统已失效部件个数。系统故障分为两类:Ⅰ类故障:系统失效部件0 假设系统发生故障时的部件失效有两种情况:①退化失效,服从威布尔分布;②随机失效,故障率随时间变化,故障发生过程是一个非齐次泊松过程。 系统更换有以下3种情况:①在N次Ⅰ类故障后预期更换;②h次Ⅰ类故障后(h X为单部件的故障时间; f(X)为随机失效变量X的概率密度函数; F(X)为随机失效变量X的累积分布函数; λ(X)为随机失效变量X的故障率函数; Y为第一次Ⅱ类故障的时间; Fα(Y)为退化失效变量Y的累积分布函数; Tj为第j次Ⅰ类故障的时间; Ci为第i次Ⅰ类故障的最小修复成本,i=1,2,3,…; CM为Ci的平均成本,CM=E[Ci]; N为系统更换前的最小修复次数,N>i; L为系统总修复成本限制; C(N)为预期成本率; Cy为预期更换产生的成本; CⅠ为由于Ⅰ类故障更换产生的成本; CⅡ为由于Ⅱ类故障更换产生的成本; Ui为更换周期的长度,i=1,2,3,…; Vi为周期Ui的运行成本; D(t)为区间[0,t]的操作系统的预期成本。 为便于维护建模,对系统作出如下基本假设: (1)系统各部件之间具有失效相关性; (2)系统的n个部件随机服从两类分布中的任意一种; (3)各个部件随役龄的增加而老化; (4)任何故障可以立刻被检测并进行处理; (5)本维护策略是基于无限时间域的。 假设系统在时间t发生Ⅰ类故障的概率为q=(1-p),发生Ⅱ类故障的概率为p(0 Y为Ⅱ类故障发生的时间,令N1(t)为(0,min(Y,t))中最小修复发生的次数,则在[0,t]中发生i次Ⅰ类故障的概率为: (1) 令Tj(j=1,2,3,…)表示第j次Ⅰ类故障发生的时间,其中T0=0,则随机变量Tj的分布函数如下: FTj|Y(t)=P(Tj≤t|Y>t) =P(N1(t)≥j|Y>t) (2) 在时间t发生j次Ⅰ类故障的概率为: =Pj-1(t)qλ(t)dt。 (3) 假设第i次Ⅰ类故障的最小修复成本Ci具有非负独立同等的分布函数: (4) (5) 系统更换有以下3种情况:①在第N次Ⅰ类故障时进行预期更换,更换成本为Cy;②若Ⅰ类故障次数未超过N,但累积维修成本已经超过预期成本L,此时对系统进行更换,Ⅰ类故障更换成本为CⅠ;③若在N次Ⅰ类故障前发生Ⅱ类故障,此时对系统进行更换,Ⅱ类故障更换成本为CⅡ。这3种情况以先发生者为准。这3种情况的相应概率如下: (1)发生关键Ⅰ类故障导致的更换概率为: P(Tj∈(t,t+dt)|Y>t)dt (6) (2)发生Ⅱ类故障导致的更换概率为: (7) (3)预期的N次Ⅰ类故障导致的更换概率为: P(TN∈(t,t+dt)|Y>t)dt (8) 在该模型中,考虑t=∞的条件下,根据上述表格的定义,系统长期的预期成本率为: (9) 根据上述3种更换方案,第一个更换周期U1的长度为: U1= (10) 第一个更换周期U1的期望长度为: t)P(Mj-1 (11) 同样的,第一个替换周期的成本V1为: (12) 则第一个替换周期的期望成本为: (t,t+dt)|Y>t)P(Mj-1 P(TN∈(t,t+dt)|Y>t)P(MN-1 (13) 式中CM=E[∑Ci]。 由于在工程实际中,影响表决系统可靠性的因素很多,系统部件之间往往具有一定的相关性,因此本文考虑了部件之间的失效相关性。 Copula函数中最常用的是阿基米德Copula,其中Gumbel Copula、Clayton Copula与Frank Copula最常见,又Gumbel Copula与k-out-of-n:F系统的相关性符合,且模拟的结果与实际更贴合,因此选用Gumbel Copula模型[18]。 则相关结构为: (14) 在t时刻系统的可靠度为: F(r+1)(t),…,F(n)(t))。 (15) 因此,系统每单位时间的长期期望成本为: (16) 威布尔故障率函数为: (17) 随机失效之间的间隔时间T是互相独立的并且服从指数分布特征: P{T>t}=e-αt,α>0。 (18) 在t时刻,随机失效导致的系统不可靠度为: F(t)={P (19) 为了验证模型的有效性,相关参数设置如下: Cy=800,CⅠ=1 000,CⅡ=1 200,L=700, θ=5,β=3,α=2,k=3,n=5。 因此,得出预期成本率C(N),最小修复次数N与时间t的图像如图1所示。 由图1可知,系统预期成本率C(N)随着最小修复次数N与时间t的增大而逐渐减小,但在达到一定数值时成本率又逐渐增大。当修复次数N=7时,预期成本率达到最低C(N)=287。由此可知,并不是维修次数越少,系统的累积修复成本就越低。 由式(16)~式(18)可知,影响C(N)与N的参数有很多,其中包括参数α、β、θ、以及各类维护成本与更换成本,通过改变这几个参数来了解它们对最优解的影响。得到的图像分别如图2~图5所示。 图2所示为根据不同的参数α,系统预期成本率C(N)随维护次数N的不同而变化的趋势。由图2可知,当α=0.5时,系统的预期成本率最低值为C(N)=186,此时的最小修复次数N=5;当α=1时,系统的最小预期成本率C(N)=243,此时的最小修复次数N=6;当α=1.5时,系统的最小预期成本率为C(N)=411,最小修复次数为N=7。 如图3所示为根据不同的参数θ,系统预期成本率C(N)随维护次数N的不同而变化的趋势。由图3可看出,当θ=10时,系统的预期成本率最低值为C(N)=186,此时的最小修复次数为N=7;当θ=15,系统的最小预期成本率C(N)=402,此时的最小修复次数N=6;当θ=20时,系统的最小预期成本率为C(N)=495,最小修复次数为N=7。 如图4所示为根据不同的参数β,系统长期预期成本率C(N)随维护次数N的不同而变化的趋势。由图4可知,当β=2时,系统的预期成本率最低值为C(N)=311,此时的最小修复次数为N=6;当β=2.5,系统的最小预期成本率C(N)=486,此时的最小修复次数为N=7;当β=3时,系统的最小预期成本率为C(N)=407,最小修复次数为N=4。 表1与图5所示为更换成本的敏感性分析。由图5可知,由Ⅰ类故障导致的更换成本CⅠ对系统的预期成本率影响较大,最小的预期成本率随着CⅠ的增大而减小。当CⅠ=1 500,Cy=800,CⅡ=1 200时,系统的最低预期成本率C(N)=211,最小维护次数N=4。而系统的最小预期成本率随着CⅡ与Cy的增大而增大。当预期更换成本Cy=600,CⅠ=1 000,CⅡ=1 200时,系统的最低预期成本率C(N)=305,最小维护次数N=7。当Ⅱ类故障导致的更换成本CⅡ=900,CⅠ=1 000,Cy=800时,系统的最低预期成本率C(N)=232,最小维护次数N=6。 表1 参数敏感性分析 由表1与图2~图5可以看出,每个参数都会对预期成本率和维护次数产生不一样的影响。其中,故障率参数β对最小修复次数N产生的影响最大,由Ⅰ类故障导致的更换成本CⅠ对系统预期成本率C(N)产生的影响最大。 为了进一步验证本文建模方法的有效性,将本文数学模型与只考虑两种失效模式,但不考虑最小修复次数的维护模型进行比较,各参数设置与上例相同,预期成本率随时间变化曲线如图6所示。 由图6可知,在考虑了最小修复次数N的情况下,系统整体的预期成本率比未考虑最小修复次数的系统低,因此采用本文的建模方法更符合工程实际。 在考虑系统故障与失效模式对系统可靠性的影响下,针对k-out-of-n:F系统,通过分析系统运行过程中产生故障的概率,本文建立了包括维护成本、故障更换成本和预期更换成本的系统总维护成本模型,基于系统可靠性的约束,求出使得预期成本率最低的维护次数。数值实验结果表明,故障率参数β与θ,以及故障导致的更换成本都对预期成本率以及维护次数有一定的影响,其中Ⅰ类故障导致的更换成本CⅠ对预期成本率的影响最大,故障率参数β对最小修复次数的影响最大,并且对于不同的维护成本限制以及故障率参数组合,该模型都能有效地找到最优的维护策略。 在实际工程应用中,由于受工作环境、工人操作方式和系统结构等多因素影响,复杂系统各部件间往往存在失效相关性、结构相关性、经济相关性等情况,针对这些复杂系统进行可靠性及维护建模是下一步的研究重点。1 维护建模
1.1 问题描述与基本假设
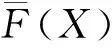
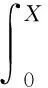
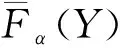
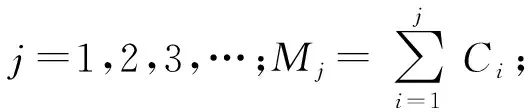
1.2 成本函数建模
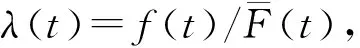
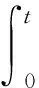
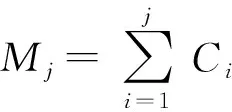












2 数值算例

3 结束语
