大型龙门式自动铺丝机空间误差建模及参数辨识

郑成淦，于杰保，张 立，吴剑波，程 亮

(浙江大学 浙江省先进制造技术重点研究实验室，浙江 杭州 310027)

0 引言

碳纤维复合材料具有比强度高、硬度大、耐腐蚀等众多优点，由该材料制成的构件具有重量低、材料性能和结构性能提升、可一体化制造等优势[1]。在世界主流航空制造企业中，复合材料在飞机零部件制造中的使用占比逐步增加，如在F22上为23%，空客A380为25%，波音787则高达50%[1]。自动铺丝机是复合材料构件制造领域中常用的高精度加工机床之一，其静态误差是影响复合材料铺丝精度的主要因素。自动铺丝机静态误差的主要来源是由机床各轴的几何误差引起的空间误差，受机床自身零件精度及装配精度影响，机床各轴的几何误差难以消除，最终影响自动铺丝机的铺丝精度。在本文的研究中，自动铺丝机处于恒温恒湿的工作环境中，热变形引起的误差可忽略；龙门式的机械结构刚度高、负载能力强，由重力和工作载荷引起的变形误差较小，因此将其视为绝对刚体进行研究。本文将针对龙门式自动铺丝机各运动轴的几何误差，重点开展关于自动铺丝机空间误差的研究。

为了研究数控机床几何误差建模方法，多年来国内外大量研究人员做了许多尝试。SCHULTSCHIK[2]基于矢量法对机床误差进行建模，并根据此误差模型研究了工作条件下的机床误差。谢春等[3]分析了车铣复合加工中心结构，并基于神经网络强大的学习能力对几何误差进行预测和补偿并建立误差模型，通过实验验证模型和补偿算法的有效性。杨枝[4]分析了数控机床的拓扑结构和低序阵列,并基于多体系统理论对其几何误差进行分析和建模。DING等[5]基于多体系统理论建立数控车床几何误差模型，并基于该模型对几何误差进行预测与补偿，通过仿真和车削实验验证其方法的有效性。在以上建模方法中，三角函数法、矢量法建模对几何误差的适用性较差，不能考虑误差耦合；基于多项式方程建模方法复杂，建模难度较大。而基于多体系统理论建模则能避免上述方法的不足，提高建模精度，更适合大型龙门式自动铺丝机几何误差的建模。

综合误差测量参数辨识法主要通过精度较高的测量仪器(如激光干涉仪、激光跟踪仪等)测量机床实际位置，通过建立运动学模型与参数识别，从而得到各误差项的具体数值。张恩忠[6]利用激光干涉仪等仪器测量机床误差并对其数据进行分析，同时基于多体系统理论建立运动学模型与几何误差模型，通过实验对模型准确性加以验证。FABIEN等[7]利用激光跟踪仪采用智能顺序多边测量策略对小型机床的体积误差和平移轴各项误差进行测量并补偿，通过实验来检测最具影响力的实验参数。陈强[8]利用激光跟踪仪测量机床所有不同位置测量点的实际位置得到其空间误差，进而对误差进行建模和参数识别，并基于仿真验证识别参数的有效性。激光跟踪仪具有可测量行程范围大、测量速度快、精度较高等优点，且测量精度高于复合材料铺放精度要求，适合自动铺丝机空间误差测量。

本文以六轴大型龙门式自动铺丝机为研究对象，基于多体系统理论建立空间误差模型，采用激光跟踪仪对自动铺丝机空间误差进行测量，采用Levenberg-Marquardt算法(LM算法)研究其辨识参数，并对空间误差模型以及辨识参数进行实验验证。

1 基于多体系统理论的自动铺丝机空间误差建模

1.1 大型龙门式自动铺丝机结构与坐标系

本文的研究对象是六轴大型龙门式工作台固定横梁移动式自动铺丝机，是六轴联动高速重载特种机床的典型代表之一，其运动结构如图1所示。

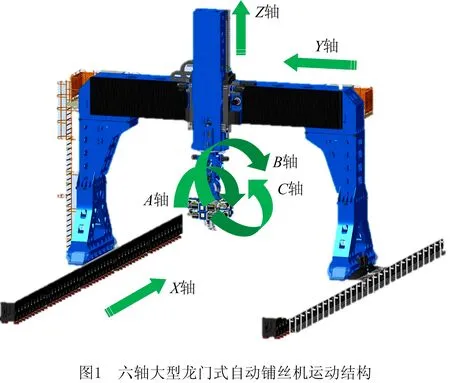
大型龙门式自动铺丝机有6个运动轴，其中X、Y、Z为平动轴，A、B、C为旋转轴，各轴行程范围如表1所示。其中，A轴、B轴旋转轴线相交于一点，C轴末端与末端执行机构(铺丝头)相连接，Z轴末端与A、B轴相连接。与传统五轴加工机床相比，六轴龙门式自动铺丝机在工作过程中不仅能保证铺丝头末端压辊的位置和法矢，还能确保压辊的切矢方向始终与路径方向一致，即压辊的前进方向始终与压辊的轴线相垂直，从而避免铺放过程中复合材料预浸料丝束出现褶皱，提高铺放精度和质量。

表1 自动铺丝机各运动轴行程范围

1.2 自动铺丝机拓扑结构

六轴大型龙门式自动铺丝机可以整体抽象为一个多体串联系统，建立自动铺丝机装配坐标系和各轴(刚体)的坐标系，所有坐标系均采用右手笛卡尔坐标系。根据多体系统理论相关公式和串联运动链理论[9]，分析可得到自动铺丝机的拓扑结构如图2所示。

1.3 自动铺丝机空间误差组成因素分析

龙门式自动铺丝机有6个运动轴，根据刚体运动特点，刚体在运动时有3个分别沿X、Y、Z轴平移的自由度以及3个绕X、Y、Z轴旋转的自由度。受零部件制造和装配精度影响，自动铺丝机各轴运动副自身存在一定的几何误差，其中运动副在空间6个自由度方向上存在几何误差，该误差与运动副在该轴行程中的位置有关，称为与位置有关的几何误差(Position Dependent Geometric Error, PDGE)[10]。同时，各轴运动副还存在与该轴行程位置无关的几何误差，在平动轴上体现为轴垂直度误差(Axis Verticality Error, AVE)，在旋转轴上体现为轴偏移误差(Axis Shift Error, ASE)。

平动轴以X轴为例进行说明，如图3所示，当移动副沿着X轴方向平动时，自动铺丝机导轨会产生6项与X轴导轨运动位置有关的几何误差(PDGE)和1项与位置无关的X轴相对于YZ平面的垂直度误差(AVE)。同理，可得到Y、Z轴的PDGE和AVE。其中：ηXY是X、Y轴之间的垂直度误差，ηXZ、ηYZ分别是Z轴与X、Y轴之间的垂直度误差，均与移动副的运动位置无关。

旋转轴以C轴为例进行说明，如图4所示，当旋转副沿着C轴方向旋转时，自动铺丝机导轨会产生6项与C轴导轨位置有关的几何误差(PDGE)和5项与位置无关的旋转轴偏移误差(ASE)。同理，可得到A、B轴的PDGE和ASE。

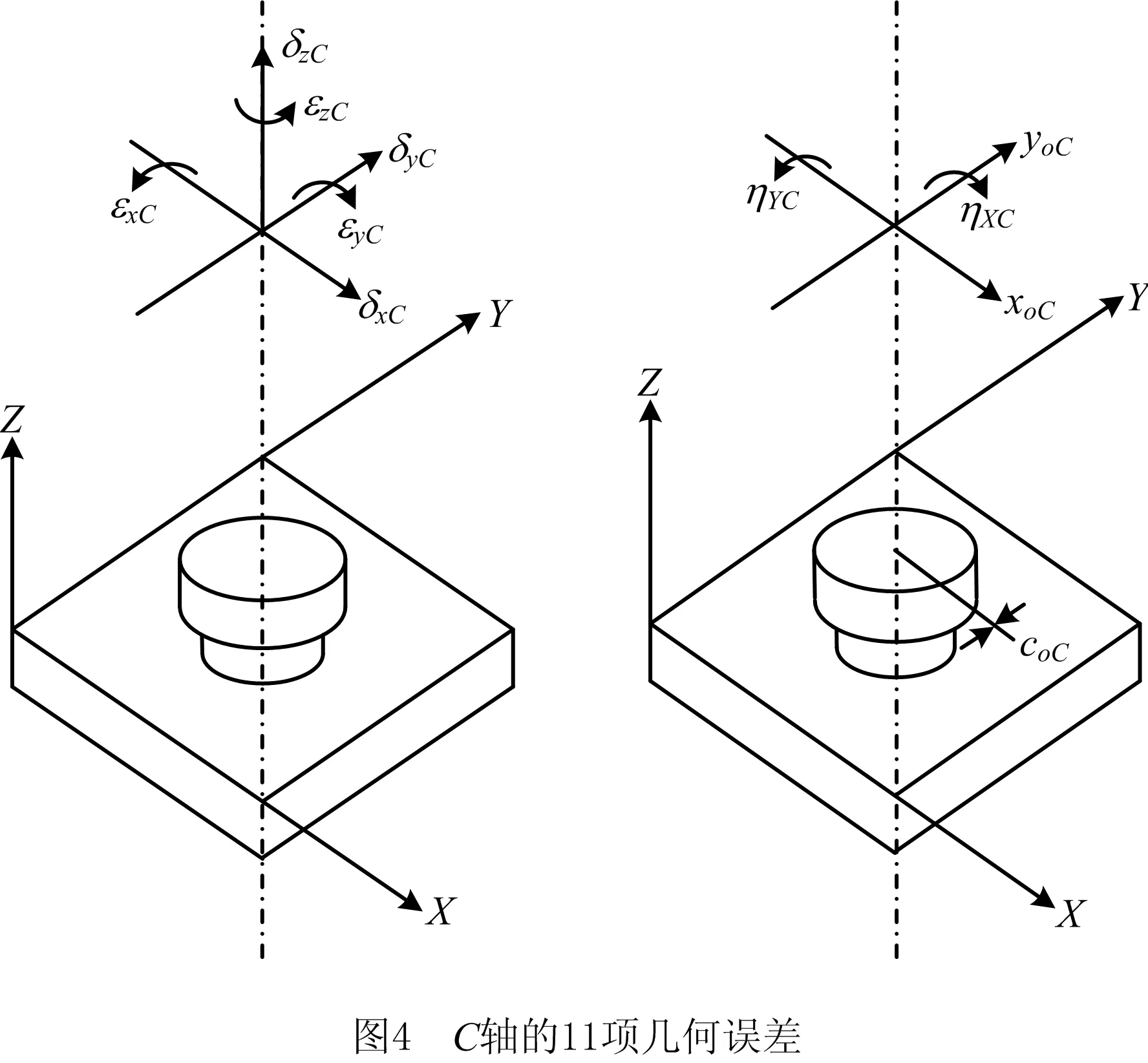
由此可见，六轴大型龙门式工作台固定横梁移动式自动铺丝机的空间误差共包含54项几何误差，并且其中36项与位置有关，18项与位置无关[11]，所有几何误差如表2所示。

表2 六轴龙门自动铺丝机54项几何误差[6,8]

1.4 自动铺丝机空间误差建模

本文中OM表示自动铺丝机装配坐标系，OH表示铺丝头末端压辊中心的位姿坐标系，OX表示X轴坐标系，其他各轴以此类推。根据多体系统理论与齐次矩阵变换，可得到各轴带有所有几何误差的位置变换矩阵[12-13]，推导过程如下：

(1)沿X轴方向移动x，OX相对于OM的带有误差的位置变换矩阵为：

(1)

(2)沿Y轴方向移动y，OY相对于OX的带有误差的位置变换矩阵为：

(2)

(3)沿Z轴方向移动z，OZ相对于OY的带有误差的位置变换矩阵为

(3)

(4)绕B轴转动θy，OB相对于OZ的带有误差的位置变换矩阵为：

(4)

(5)绕A轴转动θx，OA相对于OB的带有误差的位置变换矩阵为：

(5)

(6)绕C轴转动θz，OC相对于OA的带有误差的位置变换矩阵为：

(6)

(7)在实际情况下，利用激光跟踪仪可测量到铺丝头的压辊中心(刀尖点)相对C轴中心有偏离，则压辊中心坐标系OH相对于OC的带有误差的位置变换矩阵(相对位姿)为：

(7)

其中tx、ty、tz为激光跟踪仪测量到的偏置距离。

自动铺丝机理论运动学模型为：

(8)

自动铺丝机实际运动学模型为：

(9)

则自动铺丝机的空间误差模型为：

(10)

根据小误差假设，即sinθ≈θ、cosεab≈1，且不考虑两阶及其以上的分量，则可计算出化简之后的自动铺丝机空间误差模型空间分量为：

Δx=δxX+δxY+δxZ+xoB-coC×

(tx×(cosθysinθz-cosθzsinθxsinθy)+

ty×(cosθycosθz+sinθxsinθysinθz))…;

(11)

Δy=δyB+δyX+δyY+δyZ+yoA+ηxC×

(tx×cosθzsinθx-ty×sinθxsinθz)…;

(12)

Δz=δzX+δzY+δzZ+zoB-εyA×

(tz×sinθy+tx×cosθxcosθycosθz-

ty×cosθxcosθysinθz)…。

(13)

2 基于LM算法的自动铺丝机空间误差模型参数辨识

2.1 参数辨识目标函数及LM算法

为了自动铺丝机的加工精度和空间定位精度达到最高，需要找到一组最优的自动铺丝机空间误差模型参数，使得压辊中心(刀尖点)空间坐标的实际测量值与理想计算值之间的差距最小，即误差最小。利用激光跟踪仪测量随机空间测量点的坐标为Tm=[xiyizi]T，压辊中心(刀尖点)的理论空间坐标为Tp=[pxpypz]T，则根据实际测量值与理论计算值之间的转换关系可以得到空间误差模型参数辨识优化函数为：

(14)

f(x)是实际测量值与理论计算值之间的残差，求解残差的问题可以看作无约束非线性最小二乘问题。因此，自动铺丝机空间误差模型参数识别优化问题就是典型的无约束非线性最小二乘优化问题，即寻找到一组最优的空间误差分量模型参数值，使综合空间误差最小。则最小二乘优化目标函数为：

(15)

其中N为随机空间测量点的数目，本文中采取的测量点数目为200。

LM算法是一种常用的无约束非线性优化算法，具有牛顿法和梯度法的优点。另外，由于LM算法不需要计算海森矩阵，一般情况下通过一定次数的计算之后可以达到全局收敛，获得全局最优解，从而可以快速计算出所求模型参数的最优值，稳定性强。LM算法表达式如下[14]：

(16)

(17)

2.2 基于切比雪夫多项式的空间误差分量建模

由于部分空间误差分量与工作副位置相关，为了避免计算每个点的空间误差分量从而减少参数计算量，在采用LM算法对空间误差模型参数进行辨识优化之前，需要根据残差最小、数学逼近的原则对各相应的空间误差分量建模。本文采用切比雪夫多项式拟合法对与位置相关的空间误差分量进行建模，该方法的拟合误差随着次数增加而迅速减小，相比于最小二乘多项式拟合法精度更高。切比雪夫多项式本质是正交多项式，各个多项式之间以递归方式定义。研究表明第1类切比雪夫多项式在降低龙格现象和函数逼近方面效果极好[15]，其多项式递推关系如下列表达式所示：

T0(x)=1;

(18)

T1(x)=x;

(19)

Tn+1(x)=2xTn(x)-Tn-1(x)。

(20)

其中，自变量x的取值范围为[-1,1]，因此需要对X轴行程进行线性归一化处理，处理方法和相应的定义域转换关系为：

(21)

使用切比雪夫多项式进行拟合时，拟合精度随着多项式次数的增多而提高，但拟合效率会随着多项式次数的增多而降低。但当切比雪夫多项式用于表征几何误差时，其阶数通常会受到一定的限制。高阶切比雪夫多项式很容易将几何误差中的不可重复误差(如噪声)的影响也合并到近似函数中[16]。由于在利用激光跟踪仪测量机床点位的过程中，不可避免会产生一定的不可重复误差，过高的拟合阶数易受到噪声的影响。因此，在保证拟合精度满足自动铺丝机加工精度和空间定位精度需求的前提下，本文采用三阶切比雪夫多项式来构建空间误差分量模型。

以X轴为例，采用三阶切比雪夫多项式来构建X轴空间误差分量模型，则以切比雪夫多项式为基函数的X轴6项PDGE表达式为：

(22)

(23)

(24)

(25)

(26)

(27)

其中a、b、c、d、f、h为切比雪夫多项式基函数系数，共24项。

同理，可得到自动铺丝机其他各个运动轴的以切比雪夫多项式为基函数的PDGE表达式，共144项系数。此外，AVE与ASE共有18项，则包含18项系数，这些系数无需单独列出拟合。最终共有162项空间误差分量模型参数需要利用LM算法进行辨识优化。

2.3 空间误差模型参数辨识

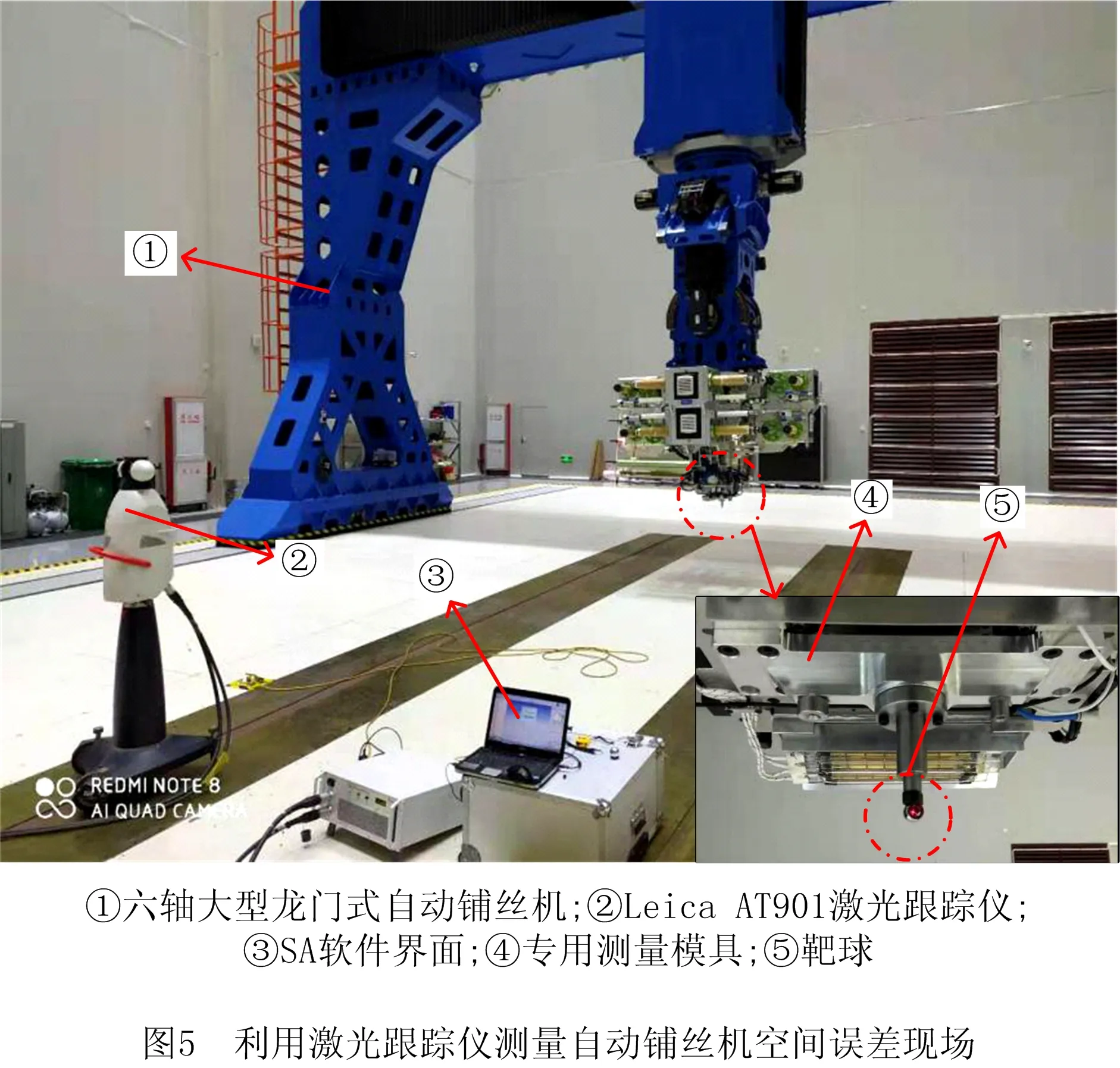
本文利用Leica AT901激光跟踪仪使用综合误差间接测量法对自动铺丝机的综合空间误差进行测量分析，通过测量铺丝机周围地面上提前布置好的ERS(enhance reference system)点的实际位置来建立自动铺丝机装配坐标系，并由此建立自动铺丝机装配坐标系与测量坐标系之间的映射关系，从而可以将各个位置的测量数据转换成统一坐标系下的位置。为了使测量数据能够真实反映铺丝机实际工作时的末端位置，将铺丝头末端的压辊机构替换为测量专用机构，将靶标座的位置设计为压辊中心位置(即刀尖点(Tool Center Point, TCP))，从而保证测量数据能够代表铺丝机实际工作时的状态。Leica AT901激光跟踪仪的几个重要测量参数如表3所示，现场测量情形如图5所示。

表3 Leica AT901激光跟踪仪测量参数

在自动铺丝机的行程范围内，随机生成180个空间位姿，其在三维空间的分布如图6所示。测量时，操控机床逐一运动到每个位姿处并测量每个位姿下铺丝头末端压辊中心的实际空间位置。在实际测量过程中，存在部分点位位置过高人员无法操作、部分点位位姿恰好挡住激光跟踪仪的测量光路等难以预测的问题，有20个点位最终没有被采用，因此剩余180个测量点作为有效测量点。

将180个随机测量点的实际位置代入自动铺丝机运动学模型，并运用MATLAB软件编写LM算法程序识别各空间误差分量模型参数，得到162个模型系数。其中各PDGE分量的切比雪夫多项式模型的144个系数如表4所示，AVE与ASE的18项误差值如表5所示。

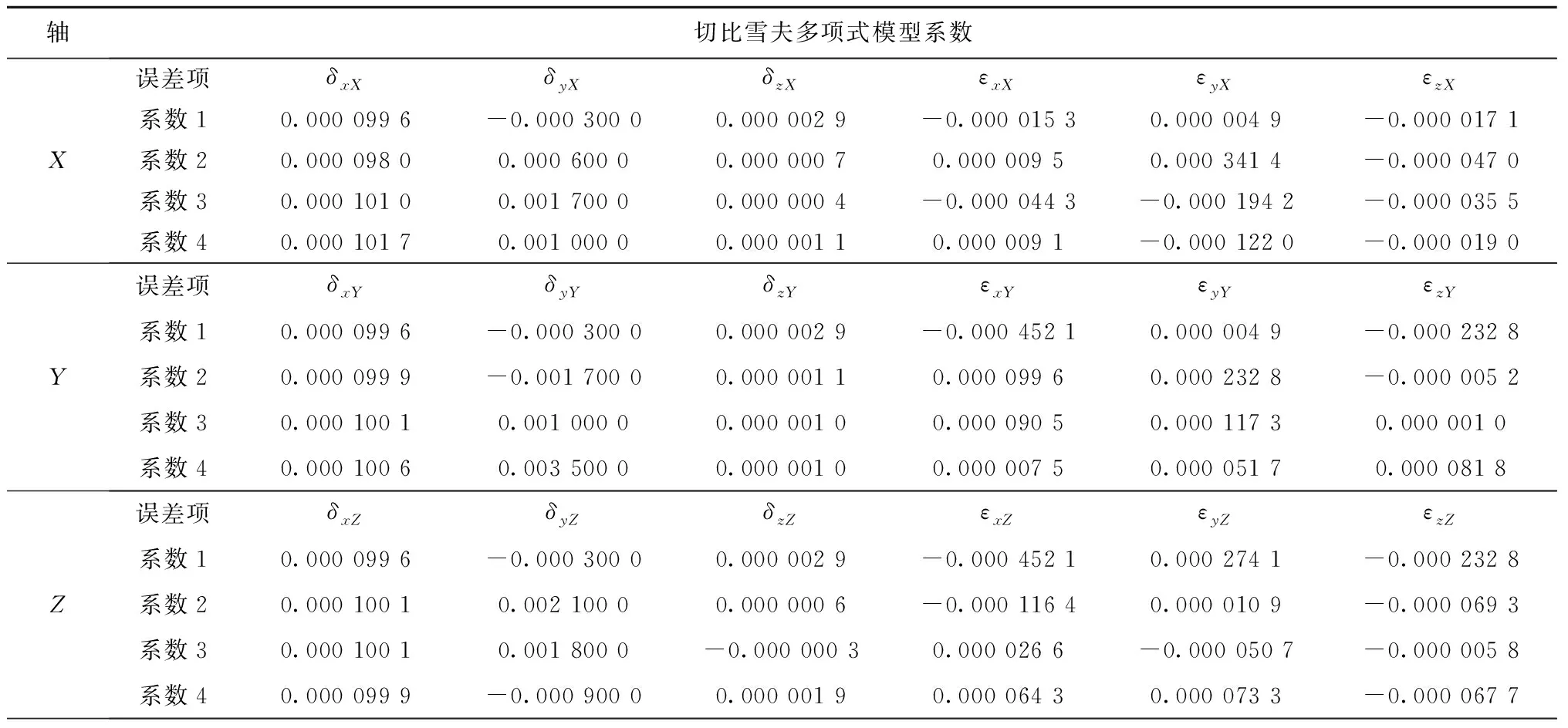
表4 各PDGE分量的切比雪夫多项式模型系数

续表4

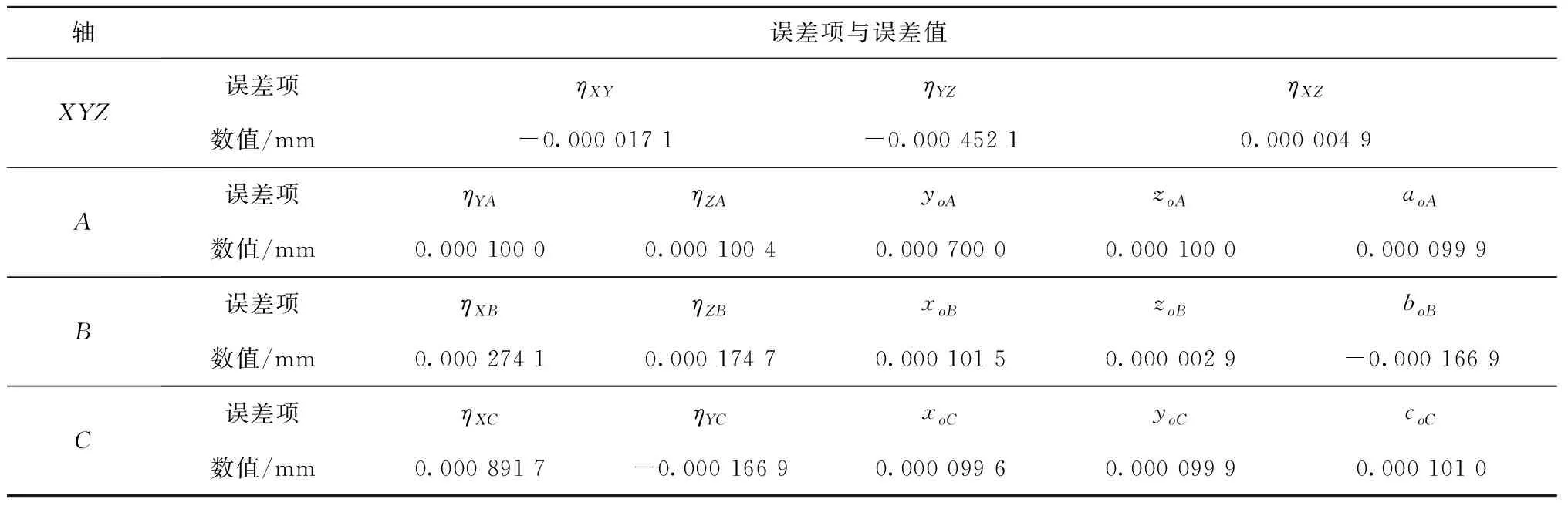
表5 AVE与ASE的误差值

根据LM算法参数辨识的结果，可得到对自动铺丝机空间误差的预测模型，将测量点各关节位置值代入模型即可得到参数辨识后各位置的空间误差。在进行参数辨识之前，自动铺丝机的运动模型为不含误差系数项的理论模型，将测量点各关节位置代入理论模型并与实际测量点位作差即可得到参数辨识前的空间误差。参数识别前后的误差最大值、均值及标准差对比如表6所示，各向空间误差对比如图7～图9所示。

表6 误差模型参数识别前后各向综合空间误差情况

可以发现：在对自动铺丝机空间误差进行建模和参数识别之后，各向空间误差的最大值减小8%以上、平均值减小14%以上、标准差减小19%以上，变化幅度明显减小，参数辨识前后的误差曲线明显分离。X向误差中有85%的点位误差小于0.8 mm，数量较辨识前增加了26%，误差分布范围收缩效果显著；Y向误差中有96%的点位误差小于0.8 mm，数量较辨识前增加了50%，误差分布范围收缩效果非常显著；Z向误差在参数识别前后误差分布变化不明显，这是因为：影响自动铺丝机末端空间位置的运动轴为Z轴、A轴与B轴，这3个运动轴受机床自身结构的影响，重力变形较大，本文的误差模型忽略了重力变形的影响，参数辨识后难以消除重力变形引起的空间误差。

3 参数辨识结果实验验证

3.1 工作空间体对角线

由于自动铺丝机的特点(刚体)以及其特殊的工作环境(恒温恒湿恒压)，利用空间体对角线测量方法测量时，得到的是忽略了热误差、力误差后只有几何误差的自动铺丝机空间误差的综合作用效果，可以在很大程度上反映出自动铺丝机的几何精度。若体对角线上的空间误差较小，则说明自动铺丝机几何精度较高，无需重新标定，体对角线测量如图10所示。

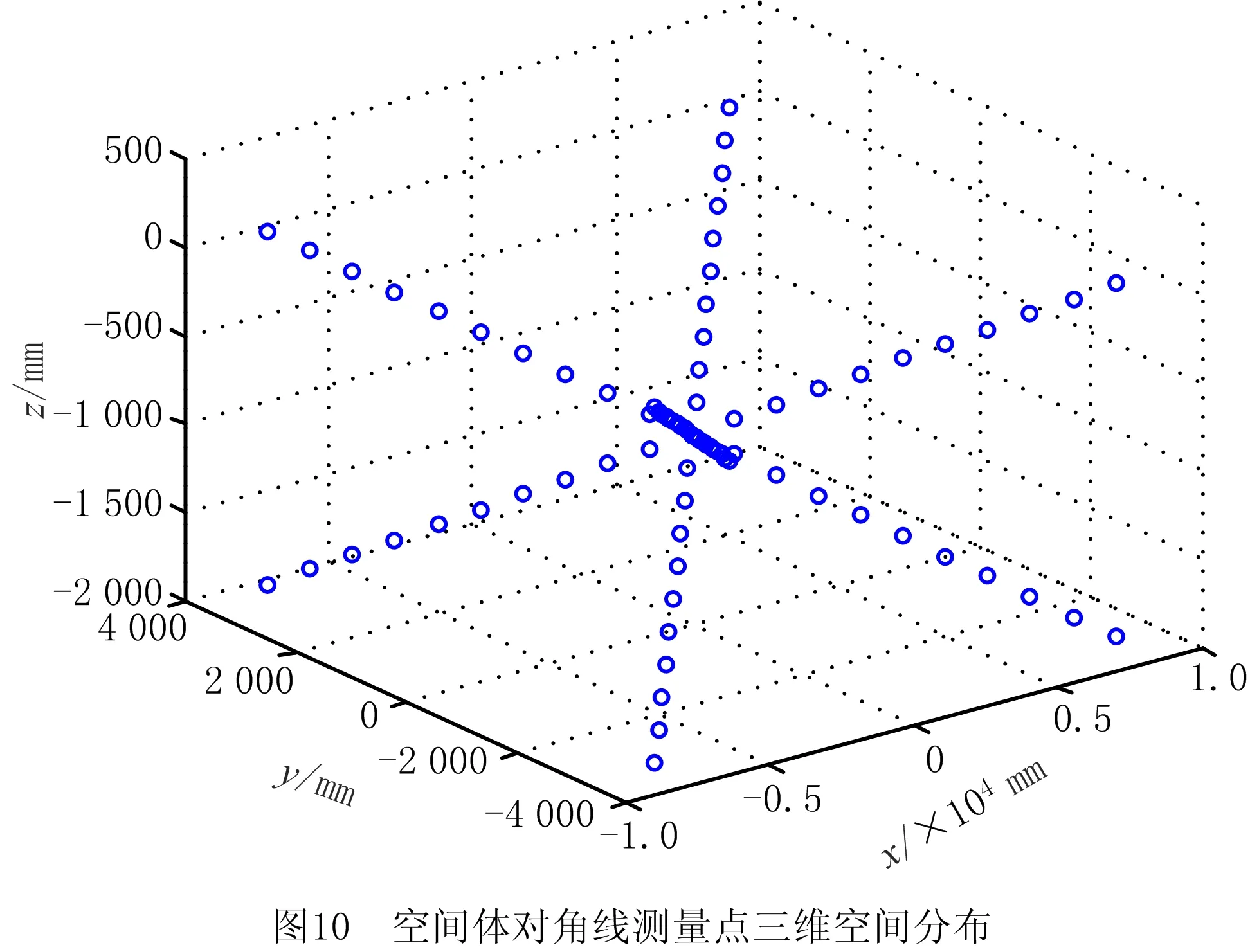
根据前文所建立的运动学模型、空间误差模型以及辨识参数，将所有的空间体对角线测量数据与关节角代入，并通过MATLAB软件计算，可以得到对自动铺丝机进行空间误差建模以及空间误差分量模型参数识别前后各向综合空间误差最大值等数值对比如表7所示，各向空间误差对比如图11～图13所示。

表7 空间体对角线上误差模型参数识别前后各向综合空间误差情况

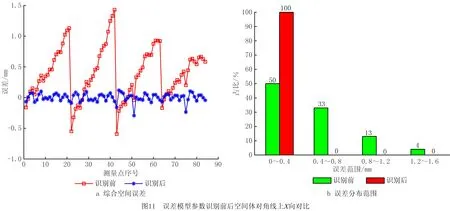
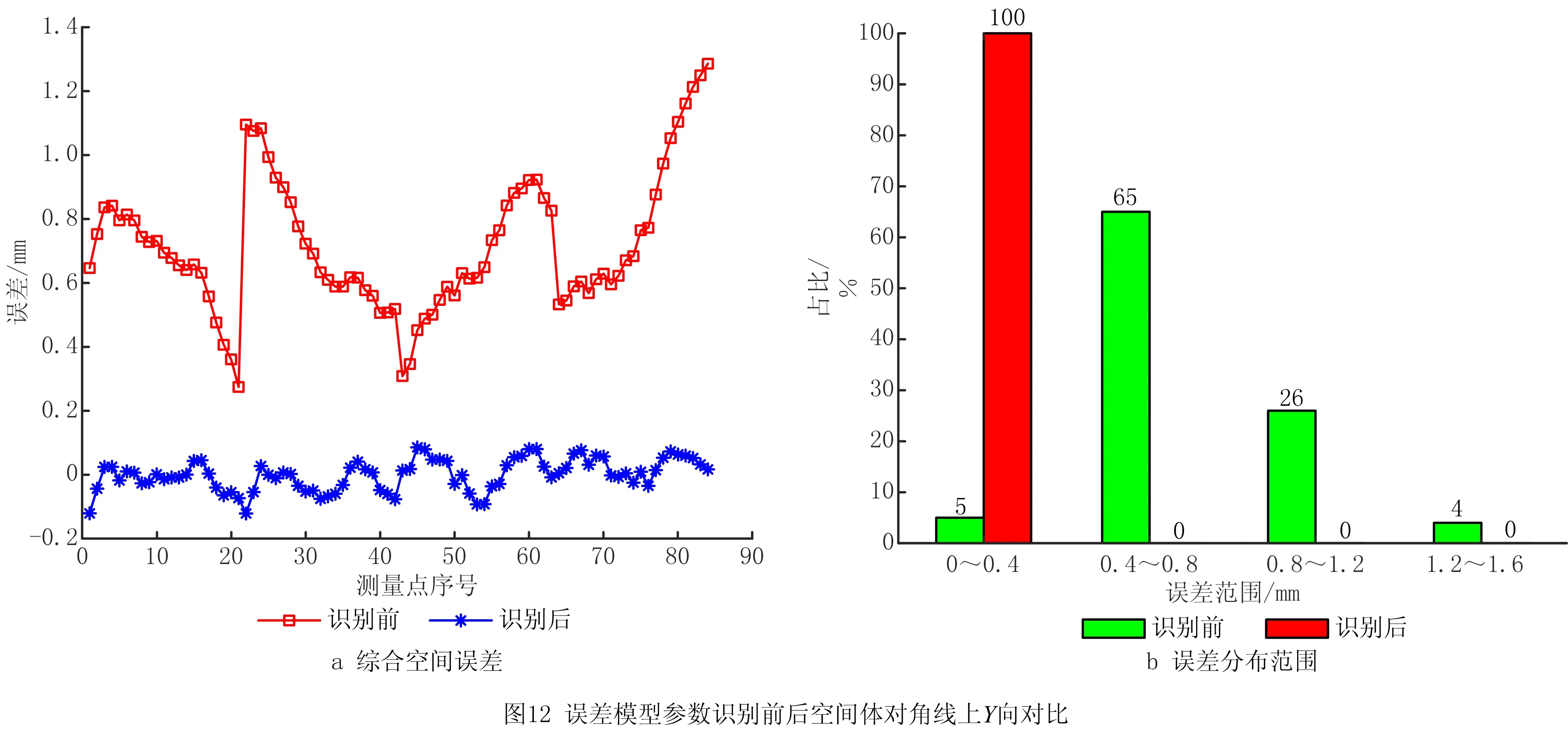
由以上图表可以发现：在对自动铺丝机空间误差进行建模和参数识别之后，各向空间误差的最大值减小70%以上、平均值减小81%以上、标准差减小81%以上，变化幅度减小效果较明显，误差曲线与建模和参数识别之前的误差曲线分离明显。X向所有点位误差均小于0.4 mm，数量较辨识前增加了50%，误差分布范围减小比较显著；Y向所有点位误差均小于0.4 mm，数量较辨识前增加了95%，误差分布范围减小非常显著；Z向误差平均值降低了81%，标准差降低了81%，误差分布范围减小非常显著。

3.2 翼梢小翼铺放路径

为了验证空间误差模型及辨识后参数的准确性，选取某国产型号飞机翼梢小翼复材构件的实际铺丝路径进行自动铺丝机压辊末端空间误差测量。选择铺层ply1的第19条路径进行测量，铺层角度为0°，如图14所示。

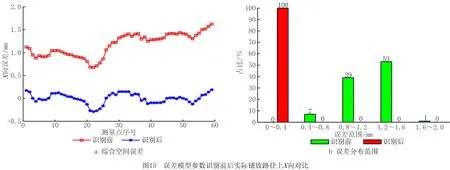
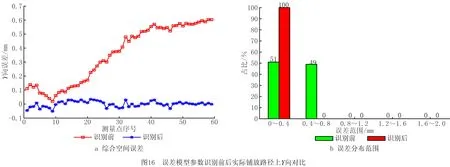
根据前文所建立的运动学模型、空间误差模型以及辨识参数，将实际铺放路径上所有测量点的实际位置与关节角代入，并通过MATLAB计算，得到对自动铺丝机进行空间误差建模以及参数识别前后的实际铺放路径上各向综合空间误差最大值等数值对比如表8所示，各向综合空间误差对比如图15～图17所示。

可以发现：在对自动铺丝机空间误差进行建模和参数识别之后，各向空间误差的最大值减小82%以上、平均值减小92%以上、标准差减小71%以上，变化幅度减小效果较明显，误差曲线与建模和参数识别之前的误差曲线分离明显。另外，X向所有点位误差均小于0.4 mm，数量较辨识前增加了100%，误差分布范围减小非常显著；Y向所有点位误差均小于0.4 mm，数量较辨识前增加了49%，误差分布范围减小比较显著；Z向所有点位误差均小于0.4 mm，数量较辨识前增加了44%，误差分布范围减小比较显著。

表8 实际铺放路径上误差模型参数识别前后各向综合空间误差情况

3.3 空间随机位姿的补偿

为了达到补偿效果，先采用本文建立的误差预测模型预测目标位姿点的误差，再根据该点误差在空间中的3个分量分别以补偿的形式代入机床G代码的空间位置中去，最终形成一套全新的空间随机位姿G代码并再次进行测量试验，补偿前后的空间随机位姿点各向综合空间误差最大值等数值对比如表9所示，各向综合空间误差对比如图18～图20所示。

从上面的图表可以看出：与补偿前的空间误差相比，补偿后各向空间误差的最大值减小33%以上、平均值减小33%以上、标准差减小39%以上，变化幅度减小效果非常明显。补偿后X向所有点位补偿误差中有84%分布在0.4 mm以内，数量较补偿前增加了41%；Y向所有点位补偿误差中有99%分布在0.4 mm以内，数量较补偿前增加了32%；Z向所有点位补偿误差中81%分布在0.4 mm以内，数量较补偿前增加了22%，分布范围大幅度减小。

表9 空间随机点位置补偿前后各向综合空间误差情况

4 结束语

本文以浙江大学自主研制的大型六轴龙门式自动铺丝机为研究对象，以减小自动铺丝机的空间误差为目标，采用基于激光跟踪仪的综合误差间接测量方法，对自动铺丝机的空间误差进行了建模、测量、模型参数辨识以及误差预测等工作。

在考虑几何误差的基础上，首先分析了自动铺丝机的空间误差影响因素，建立了基于多体串联系统理论的自动铺丝机空间误差模型并分析得出该模型包含54项模型参数，其中36项与位置有关，18项与位置无关，又以三阶切比雪夫多项式为基函数拟合36项与位置有关的几何误差，建立空间误差分量模型。利用激光跟踪仪对自动铺丝机工作空间内的随机点进行误差测量，作为模型参数辨识的数据来源，通过LM算法程序辨识优化空间误差模型参数。最后通过自动铺丝机的工作空间体对角线和ARJ21翼梢小翼壁板实际铺放路径来验证参数辨识的准确性。

本文主要基于几何误差分析与建模，获得了自动铺丝机在工作空间内误差分布规律，后续研究还应考虑大跨度横梁结构重力变形对设备末端精度的影响，进一步提高自动铺丝机的铺放精度。