双向地震荷载下崩塌堆积体盲数稳定可靠性分析

仝霄金, 丁 刚, 魏汝明, 陈训龙

(1. 济南市勘察测绘研究院, 山东 济南 250000;2. 山东省路桥集团有限公司, 山东 济南 250100;3. 华中科技大学 岩土与地下工程研究所, 湖北 武汉 430074)

0 引言

我国是一个山多且地震高发的国家,在发生地震的同时,往往还会伴随有边坡滑坡或坍塌等灾害,给人民的生命财产安全造成了巨大影响和损失[1]。因此,对于边坡抗震及支护研究一直是岩土工程界的一个热点和难点课题。

当前,地震荷载下边坡稳定性分析已取得了大量的研究成果。Latha等[2]运用了拟静力法,对喜马拉雅山脉某一顺层岩质边坡进行了地震稳定性研究。刘汉龙等[3]采用时程分析法研究了地震荷载下的边坡稳定性,并提出了新的稳定性评价指标。肖克强等[4]运用离散元软件UDEC揭露了地震荷载下边坡的位移变形特征,并进一步对坡高和坡角等进行了敏感性分析。但是,在实际中,边坡的稳定性往往受多种不确定性因素影响,如随机性、模糊性和灰色性等[5-6]。因此,在研究边坡稳定性时,应结合可靠度理论。目前,现有的边坡地震可靠性研究已得到了一些成果:龚文惠等[7]针对地震荷载和边坡岩土体参数模糊性,运用拟静力法、模糊理论和最大熵理论对地震荷载下顺层岩质边坡模糊可靠性进行了研究;陈训龙等[8]针对地震动力特性和参数随机性,采用Newmark-β法提出了地震荷载下顺层岩质边坡可靠度时程分析新方法。然而,以上研究往往仅针对岩土体参数多种不确定性中的一种或两种,并未全面地考虑其多种不确定性。盲数理论可以同时考虑参数多种不确定性[9-10],但目前运用盲数理论进行边坡地震稳定可靠性的研究还少有报道[11]。陈训龙等[12]采用盲数理论建立了一种边坡可靠性分析方法,并首次提出了采用两个新评价指标来综合评判边坡稳定可靠性,但并未考虑地震荷载的影响。可见,基于盲数理论深度分析地震荷载下边坡稳定可靠性是非常有必要的。另外,以上边坡地震稳定可靠性研究往往仅考虑了单向水平地震荷载的影响,而忽略了竖向地震荷载[13]。现有结果得出,竖向地震对边坡的稳定性状态同样影响较大[14-15]。因此,作者认为,有必要考虑竖向地震荷载的影响。拟静力法由于力学概念明确,原理简单和计算方便,在边坡抗震研究和实际工程中得到学者们的广泛应用,并写入了相关规范,成为了现有最常用的边坡抗震方法之一[16-17]。

基于此,本文采用拟静力法考虑双向地震荷载,在陈训龙建立的边坡稳定可靠性盲数模型[12]基础上,以崩塌堆积体作为分析对象,推导一种双向地震下崩塌堆积体稳定可靠性分析新方法,并进一步研究水平和竖向地震对其稳定可靠性的影响。

1 相关基本原理

1.1 拟静力法

拟静力法的核心思想[18]:在静力分析基础上考虑地震荷载对边坡的作用效应,即将地震荷载简化成一个静荷载施加在边坡体上,然后,采用极限平衡理论来计算边坡整体安全系数,其中,地震荷载值由不同的地震设防烈度进行选取。按照《水工建筑物抗震设计标准(GB 51247-2018)》[19]中的内容,水平和竖向地震作用力Qh与Qv的表达式分别如式(1)与式(2):

Qh=Wαhξαi/g

(1)

Qv=Wαvξαi/g

(2)

式中:W为岩土体重量;αh和αv分别为水平和竖直向上的地震加速度设计值,αv=2/3αh;ξ为地震荷载折减系数,一般直接取0.25;αi为岩土体质心位置的地震动态分布系数,可参照图1并运用内插计算得到,其中,h为质心的高度;αm为分布系数最大值,当地震设计烈度为Ⅶ、Ⅷ、Ⅸ时,对应αm分别取3.0、2.5和2.0;g为重力加速度,一般取9.8 m/s2。

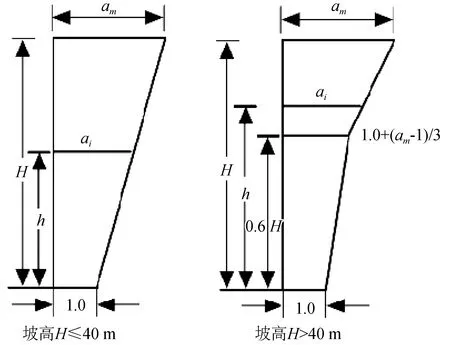
图1 地震加速度的分布系数取值参考Fig.1 Reference value of distribution coefficient of seismic acceleration

1.2 盲数概念及运算原理

(1) 盲数基本概念[12]

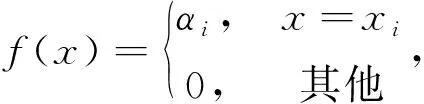
(2) 盲数的运算法则与盲数可靠度的概念

设*为运算符号+、-、×、÷中的一种,A与B为2个盲数,其表达式分别如下:

(3)

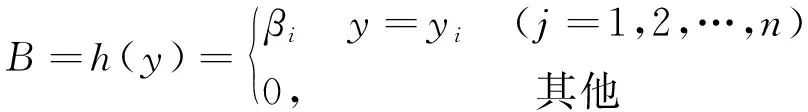
(4)

在本文中,可信度可理解为可靠度,则A和B间的运算A*B可通过可能值和可靠度两个矩阵来实现。需要注意的是,在盲数运算中,A*B中的相同元素须进行合并,当作一个元素重新进行排列,同时,在可靠度矩阵中须将相同元素对应的可靠度值进行相加,相加的结果就是该元素的最终可靠度值[12]。

在实际应用中,A*B在r处的盲数可靠度可记为P(A*B≥r),其具体计算表达式为:

(5)

其中:r为具体问题中要求值或标准值。

2 双向地震下崩塌堆积体盲数稳定可靠性分析方法

2.1 地震下崩塌堆积体极限状态方程的建立

以一单层崩塌堆积体为研究对象,根据式(1)和(2)施加双向地震荷载,选取重度γ、黏聚力c和内摩擦角φ作为基本变量,则通过响应面法[12],建立双向地震荷载下崩塌堆积体极限状态方程的响应面函数如下:

g(γ,c,φ)=Fs-1=α+ϖ1γ+ϖ2c+ϖ3φ+

χ1γ2+χ2c2+χ3φ2

(6)

式中:Fs为崩塌堆积体的安全系数,采用极限平衡法计算可得;α,ϖ1,ϖ2,ϖ3,χ1,χ2,χ3为待定系数,可由7个方程求解算得,其求解步骤可参考文献[12],其中,上述响应面函数的可靠度以及指标选用JC法[20]进行计算。

2.2 参数的盲数化处理与安全系数的盲数模型建立

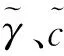
(7)

式中:γmin和γmax分别为γ的下限和上限,f1(γ)为γ的盲数;cmin和cmax分别为c的下限和上限,f2(c)为c的盲数;φmin和φmax分别为φ的下限和上限,f3(φ)为φ的盲数。

由此,根据式(6),建立崩塌堆积体地震安全系数的盲数模型如下:

Fs=α+1+ϖ1{[γmin,γmax],f1(γ)}+

ϖ2{[cmin,cmax],f2(c)}+ϖ3{[φmin,φmax],

f3(φ)}+χ1({[γmin,γmax],f1(γ)} )2+

χ2({[cmin,cmax],f2(c)})2+

χ3({[φmin,φmax],f3(φ)} )2

(8)

2.3 盲数模型解的快速输出

根据已知参数值及上述建立的模型式(8),采用MATLAB软件编写相应的计算程序,实现崩塌堆积体地震安全系数盲数解的快速输出和分析,程序的具体计算步骤如下:

(1) 根据式(8),计算出地震安全系数盲数解,并以盲数的三段式标准形式输出计算结果[如式(9),具体可根据实际需要进行区间段数划分],然后,输出双向地震荷载下崩塌堆积体稳定安全系数的累积可靠度分布曲线,并进一步通过MATLAB软件数据拟合出曲线函数(Fs-P),由此,可方便快速输出地震安全系数对应的可靠度值。

(9)

式中:Fmin,F1,F2,Fmax为安全系数;P1,P2,P3为可靠度。

(2) 根据步骤(1)算得的盲数解以及由响应面法算得的地震可靠度Pk,计算出盲数安全系数Fps,同时,由式(9)可求出最小安全要求可靠度Ps,最后,采用算得的两个指标,即盲数安全系数Fps和最小安全要求可靠度Ps,对地震下崩塌堆积体整体可靠性进行综合评判[12]。

3 算例验证与分析

3.1 工程概况及模型建立

以文献[12]中的工程算例来进行验证和分析,相关物理力学参数列于表1,该崩塌堆积体的场区抗震设防烈度设为Ⅶ度,地震相关参数如下:αh=0.10g,αm=3.0,崩塌堆积体的计算分析模型如图2所示。

表1 岩土体的基本物理力学参数Table 1 Basic physical and mechanical parameters of rock and soil

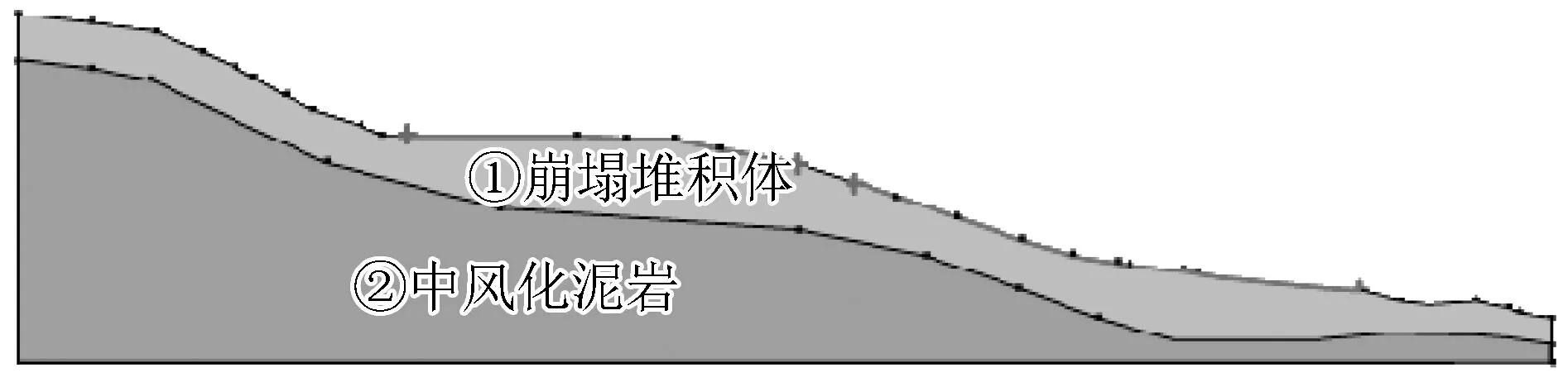
图2 崩塌堆积体的数值计算模型Fig.2 Numerical calculation model of collapse body

3.2 盲数可靠度的计算与分析

运用本文新方法,最终计算出双向地震下崩塌堆积体的可靠度Pk为56.71%,计算出其地震安全系数的盲数解列于表2。由表2可进一步输出双向地震荷载下崩塌堆积体安全系数的累积可靠度分布曲线,然后,通过MATLAB软件数据拟合出曲线函数,得到的曲线与拟合函数结果均如图3所示(其中R为相关系数)。

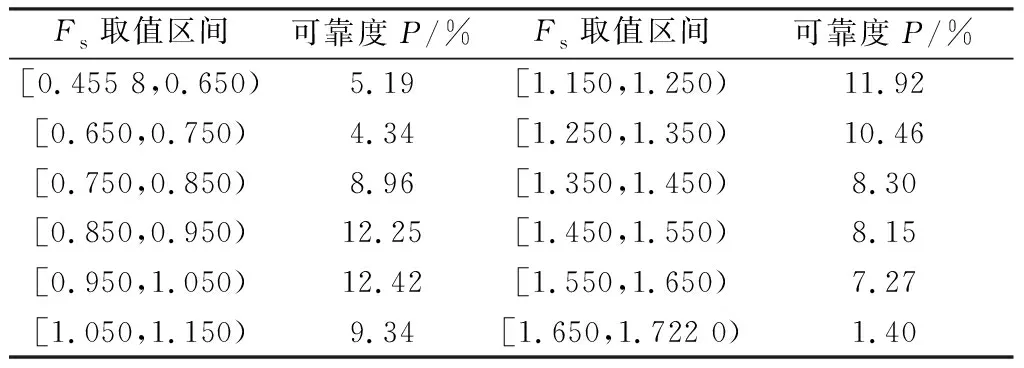
表2 双向地震荷载下崩塌堆积体安全系数盲数解

从图3可以看出,拟合函数曲线较好地重合了分布曲线,由此,可以利用此拟合函数方便快捷地输出任一地震安全系数对应的可靠度值。同时,还可以看出,随着崩塌堆积体地震安全系数取值的增大,其对应的累积可靠度呈减小趋势,表明地震安全系数取值的可靠性越来越小,其中,当地震安全系数取值为0.455 8的可靠性最大,为100%,表明取此值对崩塌堆积体的评价最安全,但易造成低估,而当取值为1.722 0时的可靠性最小,为0%,表明取此值对崩塌堆积体的评价最危险,易造成高估。

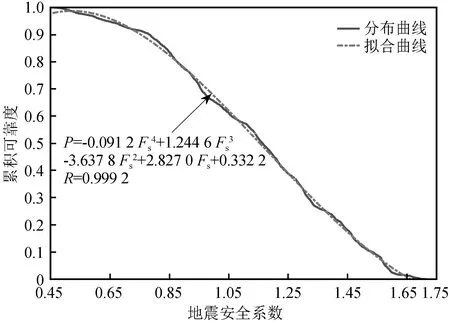
图3 地震安全系数的累积可靠度分布曲线与拟合函数曲线Fig.3 Cumulative reliability distribution curve and fitting function curve of seismic safety factor

由表2,进一步求出盲数安全系数Fps=1.051,并由该崩塌堆积体对应的稳定安全系数要求值1.30,进一步计算出最小安全要求可靠度Ps=30.35%。由Fps=1.051可知,该崩塌堆积体是偏不安全的,而由Ps=30.35%可知,该崩塌堆积体在双向地震荷载下具有较高的失稳风险。因此,综合评价该崩塌堆积体在双向地震下的稳定可靠性为偏不安全且具较高失稳风险。

3.3 对比验证分析

将本文方法与现有一般方法进行对比,结果列于表3,其中双向地震荷载均采用拟静力法考虑,方法①为采用M-P法和蒙特卡洛法算得的均值安全系数和可靠度[21];方法②是运用有限元强度折减法及响应面法得到的均值安全系数和可靠度[12]。

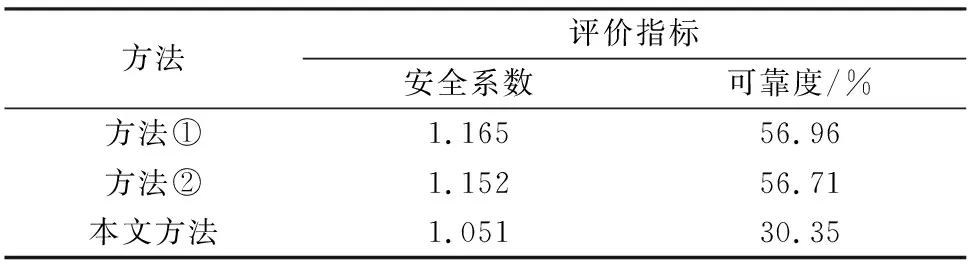
表3 各方法计算结果与比较Table 3 Calculation results and comarison of each method

由表3可以看出,本文方法的计算结果较方法①和②更低,由于本文方法考虑了岩土体参数的多种不确定性,分析的因素更全面,从而使得计算结果更可靠且更具参考价值,对工程而言也更安全,因此,本文方法是有效可行的,而且,也为边坡工程的地震稳定性研究提供一个新思路。

4 讨论与分析

基于上述研究,深度分析水平和竖向地震对崩塌堆积体整体可靠性影响,分别对以下3种工况进行分析:(1)仅考虑水平地震荷载;(2)仅考虑竖向地震荷载;(3)不考虑地震荷载[12]。需要说明的是,以上3种情况均采用本文方法计算和分析,当仅考虑水平地震荷载时,本文新方法将简化成水平地震下的稳定可靠性分析方法。通过计算和分析,各种情况的计算结果列于表4,其中(4)为考虑双向地震荷载,降低率为地震后崩塌堆积体稳定可靠性评价指标的减少量与地震前初始值之比的百分率。

从表4可以看出,在Ⅶ度地震荷载下,崩塌堆积体的安全系数降低了11.16%,而可靠度降低的幅度较大,为62.77%,表面了双向地震对崩塌堆积体整体可靠性影响很大。另外,从图中还可以看出,仅Ⅶ度水平地震荷载使得崩塌堆积体的安全系数降低了8.96%,可靠度降低了59.33%,而仅竖向地震荷载情况下的降低率分别为1.78%和2.78%,得到竖向地震对崩塌堆积体的稳定可靠性影响较小,因此,在此种工况下,采用拟静力法进行该崩塌堆积体的抗震分析时,可忽略竖向地震荷载的影响。

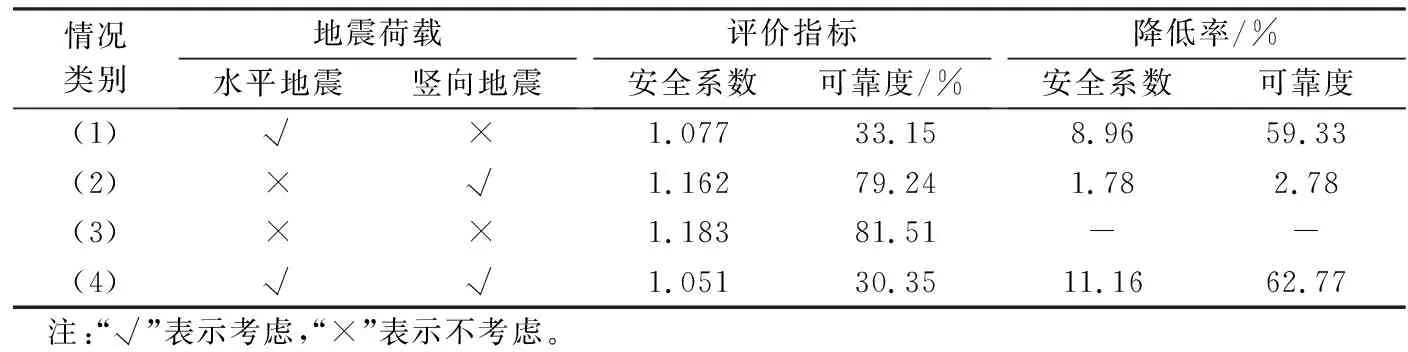
表4 地震作用效果的计算结果与比较Table 4 Calculation results and comparison of earthquake effect

5 结论

本文采用拟静力法、极限平衡法、响应面法、JC法和盲数理论建立了一种双向地震荷载下崩塌堆积体稳定可靠性分析方法。通过工程算例的验证和分析,得到的结论如以下几点:

(1) 本文方法有效可行,同时考虑了双向地震荷载和岩土体参数的多种不确定性,计算结果更可靠且更具参考价值,对工程而言也更安全。

(2) 通过拟合曲线可以快速输出任一地震安全系数对应的可靠度值,可以更全面地分析崩塌堆积体的地震安全稳定状态,并以此为根据来进行边坡抗震与加固方案设计。

(3) Ⅶ度竖向地震荷载对崩塌堆积体的稳定可靠性影响较小,在此种工况下,可仅考虑水平地震荷载。