隧道与临近地面结构动力相互作用规律数值模拟

景立平, 何 斌, 董 瑞, 李嘉瑞, 汪 刚

(1. 中国地震局工程力学研究所, 黑龙江 哈尔滨 150080;2. 防灾科技学院 地质工程学院, 河北 三河 065201)

0 引言

当今地下空间资源正在变得愈发紧张,相邻地下结构、地下结构与上部既有建筑的间距都在逐渐缩小,此时在考虑二者的地震响应时,再采用传统的将自由场地震反应分析给出的地表设计地震动参数作为上部结构输入地震动参数明显是不合适的,将地下结构-土-地上结构作为一个体系进行整体分析更符合实际情况[1]。

目前研究地下结构抗震性能的方法主要为:原型观测、模型试验和数值分析。1985年MS8.1 Michoacal地震的震后调查结果显示地铁车站的存在是导致地表临近建筑物破坏的原因之一[2]。2008年汶川地震中,发现区间盾构隧道发生明显的衬砌裂缝、剥落、错台和渗水等震害现象[3];模型试验主要包括土工离心机和振动台试验,邹炎[4]通过隧道穿过土层分界面振动台试验发现砂土和黏土动力特性以及对隧道约束作用的差异,会导致隧道穿过土层分界面时两侧的隧道地震反应不同,产生相对位移,可能会引起环向裂缝甚至整体剪断。孙海峰等[5]利用自行研制的三维叠层剪切模型箱,完成黏土层中典型三层三跨地铁车站模型的地震响应大型振动台试验,发现埋深和结构周围土层对地下结构地震响应有很大影响,揭示了地下结构地震破坏机制。Cilingir[6]对浅埋圆形隧道和方形隧道进行了动力离心机试验,结果显示圆形隧道的最大动弯矩近似位于拱肩与拱顶之间的中部,模型隧道的地震反应主要取决于输入地震动的峰值加速度,而输入地震动频谱特性的影响较小。数值分析方法随着计算机性能提升逐渐成为地震工程领域的重要研究方法,常用的数值分析方法主要包括两类:一是基于Winkler地基梁模型的反应位移法;二是基于有限单元法、有限差分法进行数值模拟。数值分析可以对模型试验结果进行预测,原型观测和模型试验结果又能对数值分析模型和方法加以改进,三者缺一不可。庄海洋等[7]在ABAQUS软件上开发的Davidenkov土体非线性本构模型在分析水平成层场地的地震反应和土-结构动力相互作用研究方面效果较好,左熹等[8]利用该土体本构模型进行了地下隧道地震反应数值模拟分析,得到边墙和拱连接处是最不利位置的模拟结论。

考虑到地上-地下结构在地震时相互影响问题,何伟等[9]、王国波等[10]进行了地下结构-土-地上结构相互作用的研究,但很多都是基于某个实际工程分析地上、地下结构的相互作用,场地的土体参数一般选择实际工程勘探结果,具有很大单一性和局限性。对于下穿隧道而言,由于其纵向尺度很大,势必会穿过各种土层,单一的场地参数难以反映实际情况。因此本文在进行隧道-土-上部结构相互作用分析时,根据《建筑抗震设计规范》设计了三类场地条件,以研究在不同场地条件下隧道-土-上部结构相互作用体系的地震响应规律。

1 计算模型

1.1 计算工况

大量的地下结构震害资料均表明,结构、地震动、场地条件是地下结构震害最主要的影响因素。结构方面,考虑有、无地下结构-土-地上结构相互作用对二者地震反应的影响;场地方面,城市中地铁隧道一般较为平整,起伏较小,但纵向尺度很大,必然会穿过很多复杂及不利土层,因此主要考虑土体性质的影响,按规范分为3类场地类别;地震动方面,已有研究表明幅值和持时与结构地震反应基本呈正相关,因此主要考虑地震波频谱特性的影响,选择El Centro波、Kobe波和迁安波进行输入。

1.2 模型参数

根据《建筑抗震设计规范》,采用等效剪切波速和覆盖层厚度两个指标将场地分为Ⅰ、Ⅱ、Ⅲ三类,这是因为在剪切波速的现场测试过程中,场地条件、土层复杂性、不均匀性、测试方法、测试条件、测试仪器等因素会造成剪切波速具有很大不确定性[11]。国内外已有相关科研成果均已证实剪切波速的不确定性对地震动参数的影响突出[12],同时考虑到第四类场地为软弱土,地质条件较差,修建隧道和临近高层的可能性较小,因此200～600 m/s的等效剪切波速变化范围能避免剪切波速不确定性的同时使研究结论更具有普适性。

根据波动理论[13],当不同土层波阻抗ρc不相等时,地震波会在分界处发生反射和折射。为避免分层过多对关注点造成干扰,将0～20 m定义为土层1,20～80 m定义为土层2,具体列于表1和表2。由于目前通用有限元软件中现有的土体非线性本构模型对于动力问题模拟结果均不太理想,要想得到较为合理的结果,通常需要进行二次开发,所需要参数较多,且大多都是针对特定类型的土体。笔者也正在进行该方面研究,考虑到本文主要进行定性分析,故文中土体仍采用弹性模型。

表1 设计场地类别

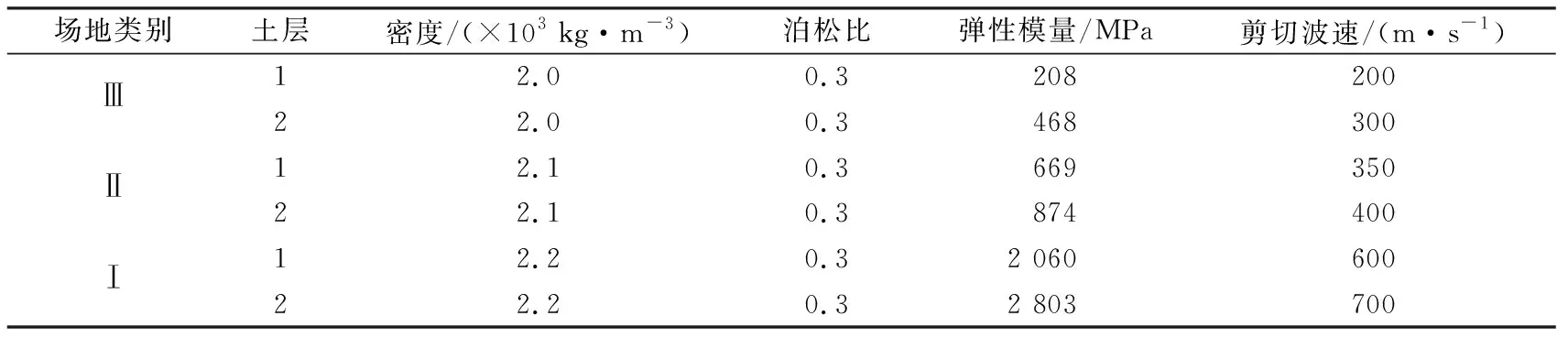
表2 材料参数

圆形隧道尺寸为直径6 m,衬砌厚度0.5 m,埋深5.5 m。一般衡量隧道地震反应的重点为内力和变形,考虑到提取内力的方便,采用平面应变梁单元进行模拟,单元尺寸1.57 m,共划分24个单元。框架结构总高45 m,水平宽度13 m,地上层高4 m,共 10 层,地下室层高 5 m,与隧道间距12.5 m。其中柱截面为 600 mm×600 mm,地基梁截面为 300 mm×800 mm,框架梁截面为 250 mm×600 mm,楼板厚度150 mm,基础楼板厚度300 mm;中柱间距3 m,与边柱间距5 m。上部结构采用平面应变梁单元进行模拟,单元尺寸1 m。混凝土杨氏模量3×104MPa,密度2.5×103kg/m3,泊松比0.2。同时由于框架结构地上部分未受到土体约束,反射波会在土体表面不断反射回上部结构,造成框架结构位移值异常,因此对高层框架结构施加一定阻尼是十分有必要的。本文通过前三阶频率的最大值和最小值作为频率范围,计算瑞利阻尼系数,给上部框架结构施加5%的瑞利阻尼。有限元模型(图1)采用动力显式积分方法进行求解,稳定时间增量步长2×10-4s。

图1 有限元模型Fig.1 Finite element model

1.3 人工边界

对于平面波垂直入射,底边界采用黏性边界吸收能量以模拟无限地基的实际情况。已有研究[14-16]及笔者对自由场两种边界条件下的地震响应进行对比,均表明当采用固定边界时,波会在底边界发生反射回到模型内部,对位移有非常明显的影响。本文侧边界采用自由度绑定边界(TDOF),通过ABAQUS中的MPC-Tie约束绑定土体模型两端同一水平高度的两个节点,巧妙地利用侧边界对应节点间的力学关系以精确模拟半无限成层场地的近场波动问题。根据Li Yang等[17]和Zienkiewicz等[18]的研究表明,TDOF边界在地震动作用下的土结相互作用分析中表现很好,优于黏弹性边界;底边界采用ABAQUS中提供的无限元进行模拟,其借鉴了黏性边界的理论,通过在单元本身引入阻尼系数来确保任何入射情况都不会产生反射波,与实际地基无限域情况相符。

图2为对TDOF边界的一个简单验证。对不同侧边距自由场模型输入脉冲荷载,监测土体表面中点的速度响应,并与远置边界结果进行对比,结果显示TDOF边界在侧边距为3R(R为结构尺寸)时就能达到较高精度,节省了大量计算时间,所以在地震反应分析中将TDOF边界用于有限元模型侧边界的模拟效果很好,能同时兼顾计算效率和精度。

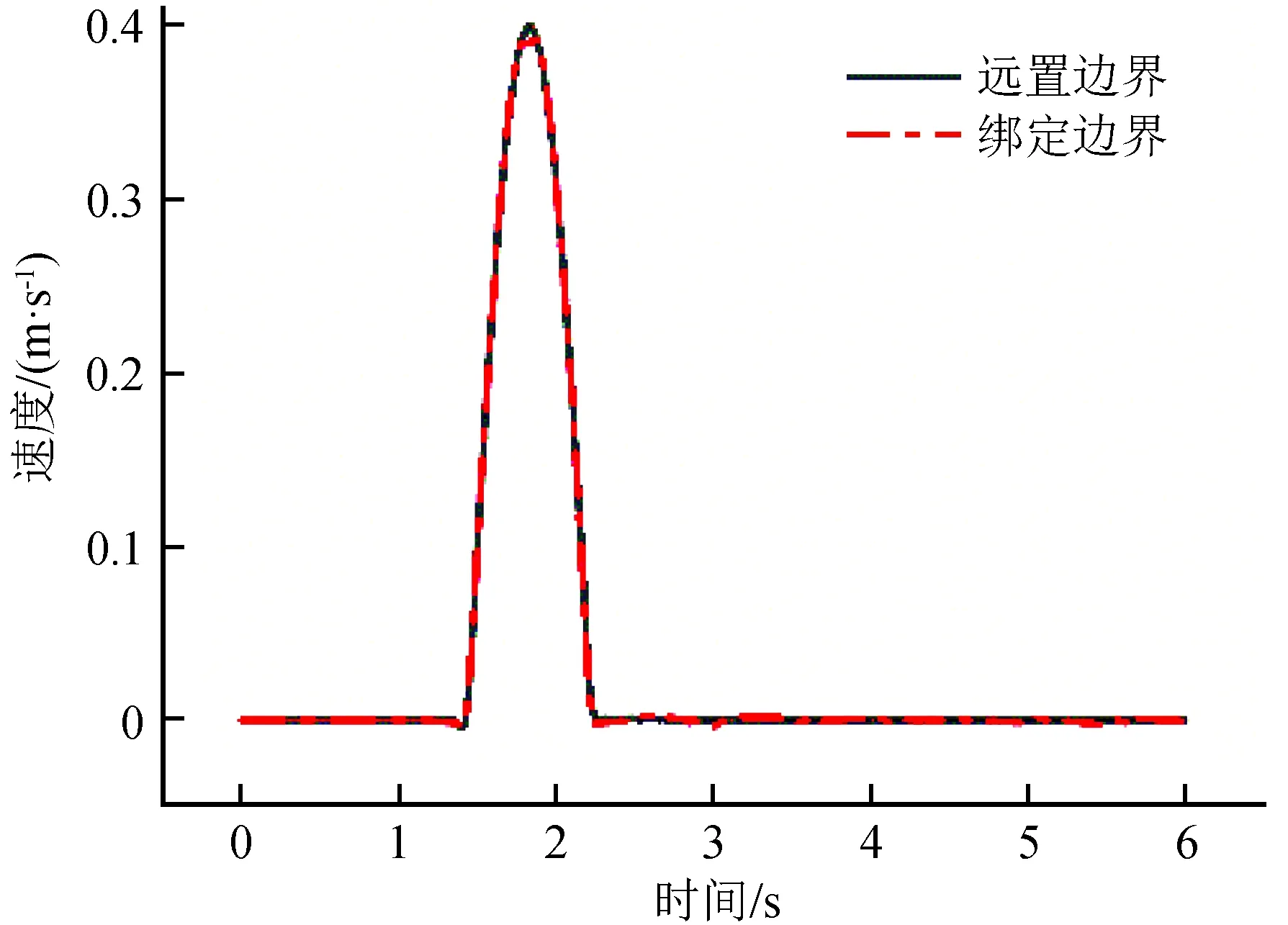
图2 自由场监测点速度时程Fig.2 Velocity time history of free field monitoring point

1.4 地震波输入

本次地震波数据选择El Centro波、Kobe波和迁安波,统一将加速度幅值调为0.2g,以研究频谱成分对结构-土-结构动力相互作用的影响。在无限单元和有限单元分界节点处施加-2ρcsv(t)的节点力模拟地震波输入,其中v(t)为地震动加速度积分得到的速度时程。加速度时程及其傅里叶谱如图3所示。

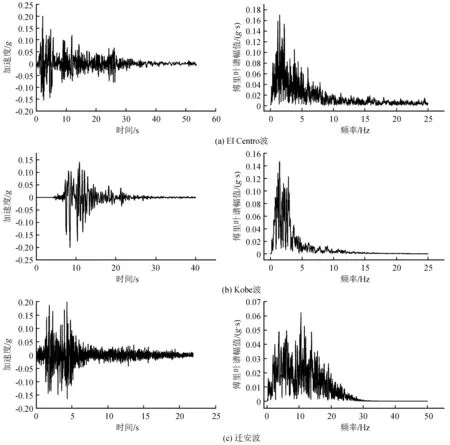
图3 输入的地震波加速度时程和傅里叶谱Fig.3 Acceleration time history of input seismic wave and the Fourier spectrum

2 动力响应分析

2.1 模态分析

表3和图4为三类场地下隧道及上部结构相互作用模型体系的前二阶频率和第一振型。可以看出:对于自由场地,场地条件越软,自振频率越低。隧道-土-结构相互作用模型的第一振型和频率主要体现的是上部框架结构的振动特性,第二频率才反映的是土体的横向剪切变形。

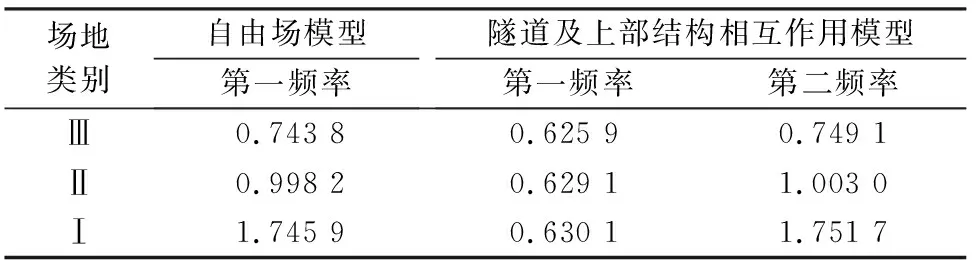
表3 不同场地下两种模型的自振频率

图4 不同场地条件下体系第一振型Fig.4 First-order vibration modes of different sites

2.2 结果分析

2.2.1 场地条件及有、无上部结构存在对隧道地震反应的影响

图5、图6分别为三类场地条件下输入El Centro波时隧道的位移响应和动内力响应。

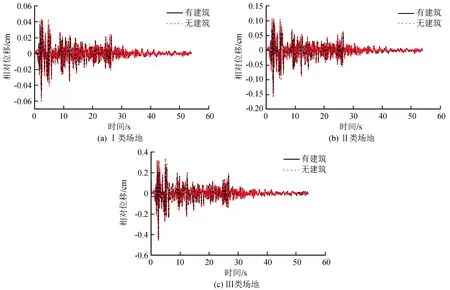
图5 隧道顶部相对于底部水平位移时程曲线Fig.5 Time history curve of horizontal displacement at the tunnel top relative to the bottom

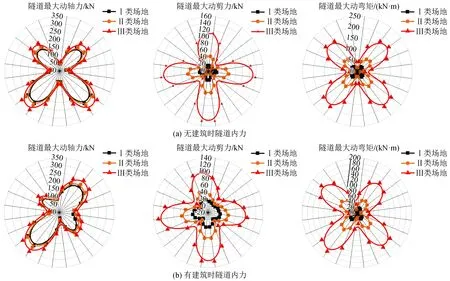
图6 隧道动内力包络图Fig.6 Envelope diagram of dynamic internal force of tunnel

对于位移响应,从图5隧道顶水平相对位移时程曲线可以看出,场地条件的影响十分明显,Ⅰ～Ⅲ类场地隧道顶水平相对位移最大值分别为:0.06(0.06) cm、0.15 (0.16) cm、0.44(0.46) cm,其中括号内为无上部框架结构时的位移值。随着场地变软,隧道位移值显著增大,Ⅲ类场地相对位移值能达到Ⅰ类场地时的7倍,这主要是因为地下结构变形受周围土体控制,周围土体越软地震时永久位移引起的附加作用越大,造成隧道内力和变形也更大;而有、无上部结构对隧道的位移反应在三类场地下影响都很小,可忽略不计。

对于动内力响应,图6为有、无上部结构时三类场地条件下的隧道动内力峰值分布图,从图中可以看到:

(1) 场地条件越软,隧道动内力越大。不同场地动轴力变化幅度较小,但动剪力和动弯矩的变化则非常明显。无建筑(上部框架结构)时,Ⅲ类和Ⅰ类场地最大动轴力相差约1.2倍;最大动剪力Ⅲ类场地为145 kN,Ⅰ类场地为25 kN,相差5.8倍;最大动弯矩Ⅲ类场地为202 kN·m,Ⅰ类场地为34 kN·m,相差5.9倍;有建筑时结果近似。

(2) S波垂直入射时,对于无上部结构体系,隧道动内力响应呈对称性,最大轴力和弯矩出现在与水平面成45°角、135°处,最大剪力出现在隧道顶部、底部和左右侧壁中央。从图6还可以发现上部结构的存在会打破动内力响应的对称性,使隧道与邻近上部结构相邻侧45°角处动轴力增大,另一侧135°角处显著减小。

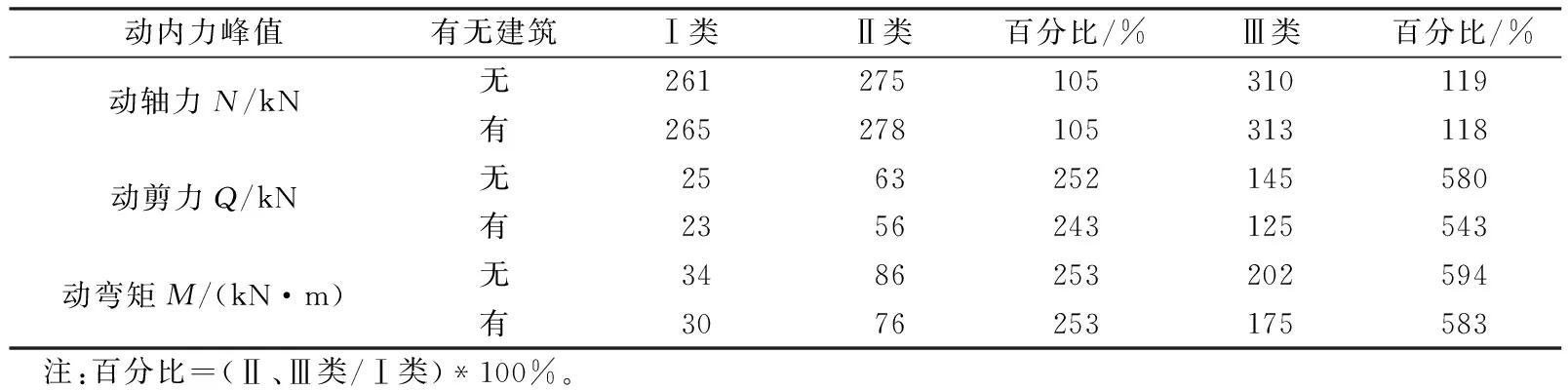
表4 隧道动内力峰值(单位:kN)

(3) 有、无上部建筑存在对隧道的动内力值会产生一定影响,但与场地条件造成的影响相比则非常小,场地条件仍是决定隧道(地下结构)地震响应的最主要因素。

2.2.2 频谱特性的影响

为研究波的频谱特性对地上、地下结构的地震反应的影响,分别输入El Centro波、Kobe波,和迁安波进行时程分析。

从图7可以看出,El Centro波、Kobe波的隧道动内力峰值在三类场地下都很接近,且明显大于迁安波的结果。对比图2发现,这是由于3条波频谱成分不同导致,El Centro波和Kobe波频率主要集中在0～5 Hz,而迁安波高频成分较多,存在很多10～20 Hz的频率,假设加速度幅值为A,两次积分后的位移幅值则为-A/ω2,频率越高,位移幅值则越小,而地下结构的地震反应主要受周围土体变形控制,土体变形位移越大,隧道的地震反应也更强烈。对于隧道动轴力还可以看出,三类场地下结构对于地震动频谱的响应也是不相同的,El Centro波和Kobe波等低频成分较多的波,中软土(Ⅲ类场地)条件下动轴力较大,对于迁安波等高频成分较多的波,硬土(Ⅰ类场地)条件下动轴力较大。

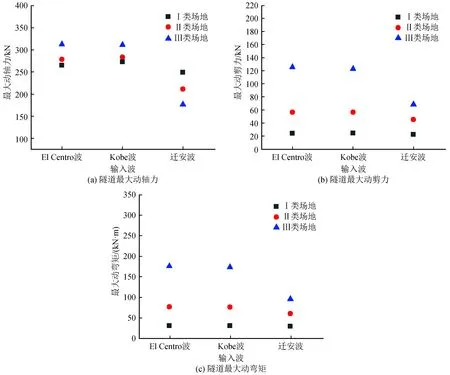
图7 不同波输入下隧道动内力峰值Fig.7 Peak value of dynamic internal force of tunnel under the input of different waves

图8为不同地震波输入下楼顶最大水平相对位移在不同场地下的对比。对比上文可以发现,地上结构与地下结构在不同波输入时的地震反应存在很大差别。对于地下结构,其内力和变形主要还是受周围土体的变形控制,而对于地上结构,地基土起着地震波的传播介质和结构基础支承的双重作用,因此上部结构地震响应受土体和地震波特性影响均较大,对于Kobe波和迁安波,三类场地下的最大位移值较接近,El Centro波时三类场地的结果则有一定差别。

图8 不同波输入下楼顶相对于楼底最大水平相对位移Fig.8 Maximum horizontal relative displacement of roof relative to floor under different wave input

3 结论

本文通过建立不同场地条件下的隧道-土-上部结构相互作用模型,研究了有、无上部结构存在、场地条件和地震波频谱特性对隧道-土-上部结构体系地震响应的影响。计算结果表明:

(1) 隧道在地震荷载作用下的位移和内力响应主要受场地条件的影响,不同场地条件隧道动轴力相差不大,但是动剪力和动弯矩值相差巨大,应引起足够重视。有、无邻近上部结构影响则较小,因此进行下穿隧道设计时,在考虑隧道与上部结构相互作用的同时,更应该重点关注隧道穿过的场地条件及其引起的弯矩、剪力变化。

(2) S波垂直入射时,对于无上部结构体系,隧道动内力响应呈对称性,最大轴力和弯矩出现在与水平面成45°角、135°处,最大剪力出现在隧道顶部、底部和左右侧壁中央;上部结构的存在会打破该对称性,使隧道与邻近上部结构相邻侧45°角处动轴力增大,另一侧135°角处显著减小,因此在进行地铁隧道设计时应考虑到临近结构的存在对隧道内力分布形式变化的影响。

(3) 波的频谱特性对地上、地下结构的地震反应的影响差异明显,地上结构受地震波输入和场地条件的影响较地下结构更大;对于地下结构,频谱特性和场地条件共同影响其地震响应,但主要由土体变形控制。