基于L1正则化逻辑回归模型的速度大脉冲预测及影响因素分析

牛志辉, 陈 波,卜春尧

(中国地震局地球物理研究所, 北京 100081)

0 引言

Berrero等[1]指出近断层地震动中含有大幅值、长周期的速度大脉冲,这种速度大脉冲对结构具有严重的破坏作用。在1957年的Port Hueneme地震中,记录到一种速度时程中含有大脉冲的地震动[2]。尽管该次地震矩震级仅为4.7,但是其所造成的灾难是同等震级地震中前所未有的。研究表明,该次地震产生的地震动时程中所含有的速度大脉冲是造成严重损失的主要原因。1994年美国Northridge地震和1995年日本Kobe地震中都发现了这种速度大脉冲强地震动记录[3-4]。由于受这两次地震影响的城市群普遍采用了现代抗震措施,地震造成的人员伤亡大大减少,但最终统计发现结构加固维修费用大大超过了人们的预期[5]。因此,预测一个地点的地震动是否含有速度大脉冲对于概率地震危险性分析和减轻地震灾害有重要的作用。

目前,国内外相关专家在预测速度大脉冲以及速度大脉冲的影响因素方面做了大量研究工作。Iervolino等[6]考虑场地与震源之间的几何参数,利用逻辑回归的方法进行了速度大脉冲概率分析。Shahi等[7]针对特定地震事件考虑震源与场地之间的几何条件,利用逻辑回归的方法建立了速度大脉冲概率模型。Fayjaloun等[8]探索了脉冲周期与描述破裂过程相关参数(包括距离、断层破裂速度、土层剪切波速)的关系,建立了速度大脉冲周期计算公式。姜兵等[9]从地震动强度参数和频谱特性角度研究了场地条件对脉冲型地震动的影响。地震动是由3个物理过程(地震破裂过程、波在地壳介质中的传播过程、场地反应)组成的一种复杂系统的产物,对于近断层,地震动的空间分布受到发震断层方位(位置、埋深等)、断层破裂面上滑动分布不均匀性和破裂过程的影响[10]。以上预测速度大脉冲的研究没有综合考虑地震动的影响条件(例如震级、距离、场地条件、震源深度等)对速度大脉冲的影响。另外,上述研究在对数据进行拟合分析时采用的多为传统的逻辑回归方法,该方法没有考虑惩罚项的引入,因此经常出现数据过拟合的情况。所以上述研究分析中有关速度大脉冲的预测效果仍具有一定的提升空间。

本文从美国NGA数据库中选取315条强震动记录,其中包含速度大脉冲的地震动153条,不包含速度大脉冲的地震动162条。对所选取的地震动记录进行预处理,剔除地震动信息不完整的记录,剩余289条记录(134条速度大脉冲记录,155条非速度大脉冲记录)。依据相对频度分析方法,分别研究震级(Earthquake Magnitude)、震源深度(Hypocenter Depth)、场地条件(vS30)、震源与场地之间的几何条件[包括震中距(EpiD)、震源距(HypD)、坎布尔距离(Campbell R Dist)、乔纳布尔距离(Joyner-Boore Dist)、均方根距离(RmsD)、距离破裂区最近距离(ClstD)、场地与断层方向夹角(Source to Site Azimuth)][11]对速度大脉冲发生的影响。并进一步基于L1正则化逻辑回归方法,建立速度大脉冲预测模型,对模型影响因素的敏感性进行分析。最后,选取符合模型数据分布规律的35条汶川地震实测数据对建立的预测模型进行验证。

1 L1正则化逻辑回归模型及评价指标

1.1 逻辑回归模型

逻辑回归是一种分类模型,由条件概率分布P(Y|X)表示,形式为参数化的逻辑分布。其中,随机变量X取值为实数,在本文中为不同因素的取值(如震级7、震中距43);随机变量Y取值为1或0,在本文中用1代表发生速度大脉冲,0代表不发生速度大脉冲。逻辑回归是如式(1)、(2)所示的条件概率分布[12]:

(1)

(2)

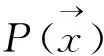
(3)

式(3)由式(1)、(2)变换可得式(4):

(4)

(5)

式中:yi(0,1)代表是否发生速度大脉冲。

1.2 L1正则化

无正则项的传统方法[7,13]往往选取比所需模型复杂度更高的模型,以提高训练数据的预测能力,进而实现更好的回归分析效果。但在实际测试中,由于不具备良好的泛化能力,容易造成“过拟合”,不利于建立速度大脉冲预测逻辑回归模型。针对该问题,本文采用L1正则化方法,在对数似然函数[式(5)]中引入正则化项,如式(6)所示:

(6)

式中:∂参数主要控制正则化强弱;wi表示不同的权重系数。

1.3 模型评价指标

本文利用接受者操作特征曲线(receiver operating characteristic curve,ROC)下方面积(area under curve,AUC)作为评价指标。AUC综合考虑了灵敏度、特异度,是目前模型评价的标准方法[15-16]。在评价过程中,AUC值越大则代表该模型的效果越理想。

2 数据集收集及预处理

2.1 数据集收集

本文回归分析所用的的315条地震数据来源于美国NGA(next generation attenuation relationships,NGA)数据库[11]。为保证数据的准确性,从Zhai等[17]的研究中获取相应的315条地震动记录编号,然后从NGA数据库下载。在Zhai等[17]的研究中,给出了195条包含速度大脉冲的记录,其中153条记录与Baker[18]识别结果一致。因此选取这153条记录作为速度大脉冲数据集,包含速度大脉冲地震动信息(表1);Zhai与Baker同时认为不含速度大脉冲的162条记录作为不含速度大脉冲数据集,不包含速度大脉冲地震动信息(表1)。

2.2 相关因素收集

地震动是由3个物理过程(地震破裂过程、波在地壳介质中的传播过程、场地反应)组成的一种复杂系统的产物。根据文献[7-8,13,19]给出的相关研究,选择出10个相关因素,包括震源因素、传播路径以及场地因素,分别为震级、震源深度、场地条件、震中距、震源距、坎布尔距离、乔纳布尔距离、均方根距离、距离破裂区最近距离、场地与断层方向夹角。详细信息列于表1和表2。

2.3 数据预处理

从表1和表2可以看出,有的数据出现缺失。为保证数据的原始性、准确性,采用空值删除的处理方法。删除有空值的记录后剩余289条记录,包括134速度大脉冲记录和155条非速度大脉冲记录。在建立逻辑模型的过程中,选取75%作为回归分析样本,25%作为测试样本,用来计算AUC值。

3 基于相对频度分析

利用本文选取的289条记录,基于相对频度分析不同因素对速度大脉冲的影响。在图1～10中,红色阴影部分表示速度大脉冲频度高于非速度大脉冲频度,蓝色阴影部分表示非速度大脉冲频度高于速度大脉冲频度。

从图1可以看出,在一定震级范围内速度大脉冲发生的频度总体上随着震级的增大呈增加趋势。震级越大释放能量越高,符合速度大脉冲具有高能量的特点。对比速度大脉冲与非速度大脉冲的频度曲线,可以发现在小于6.6级时,速度大脉冲的频度高于非速度脉冲;而在大于6.6级时,并没有此种明显的特征。这表明仅仅考虑震级对速度大脉冲的影响是不够的。

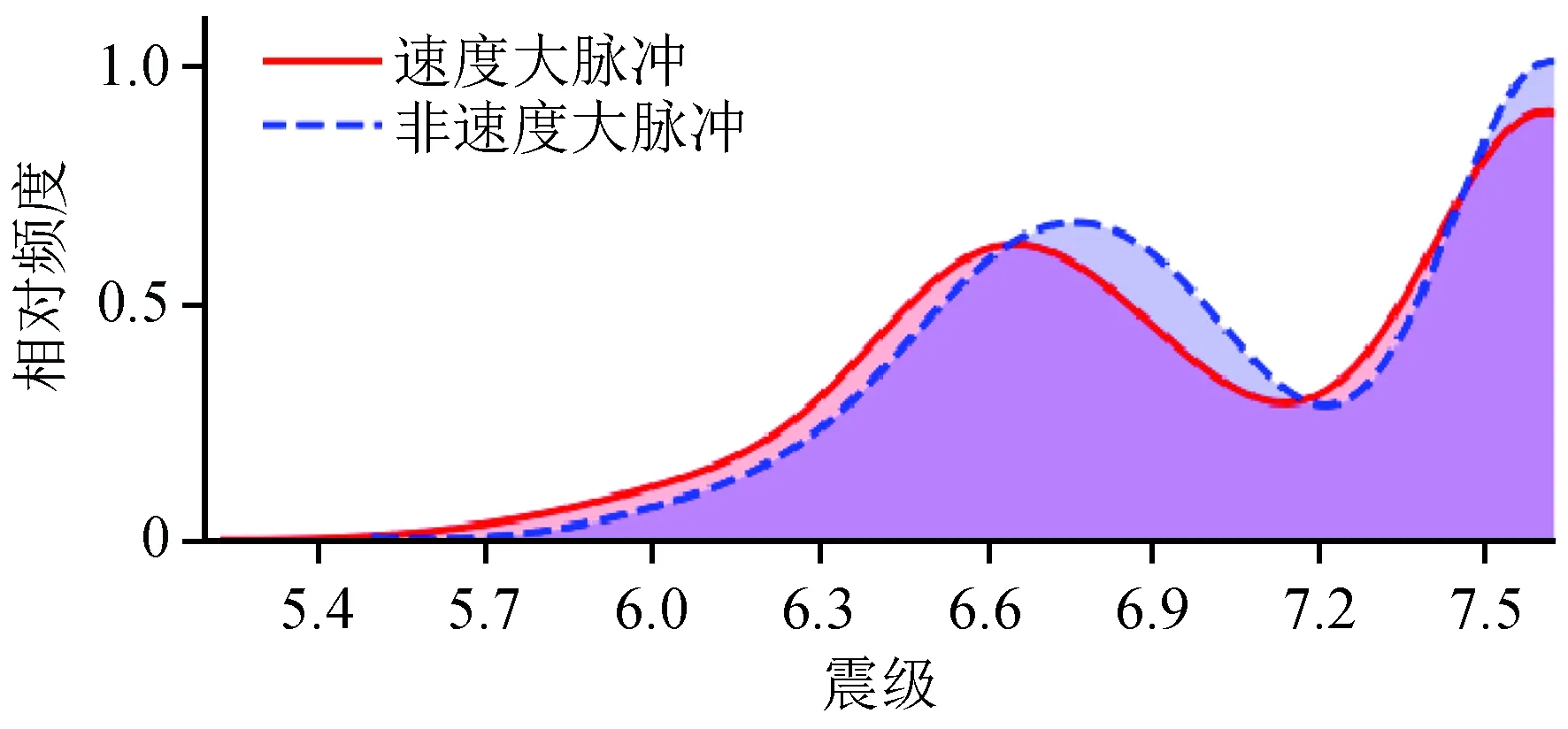
图1 震级与速度大脉冲的关系Fig.1 The relationship between magnitude and big velocity pulse

自20世纪90年代以来,vS30是评价场地条件的重要参数[20],本文用vS30表示场地条件。图2展示了场地条件与速度大脉冲的关系。可以看出,当剪切波速小于276 m/s时,随着剪切波速增大,速度大脉冲频度增大;当剪切波速等于276 m/s时,速度大脉冲频度达到峰值;当剪切波速大于276 m/s时,速度大脉冲发生频度逐渐减小。两类频度曲线仅在200～320 m/s范围内出现较明显的差异,速度大脉冲在较小剪切波速场地的发生频度较大,因此在重大工程选址时应该选择基岩等场地条件较好的位置。

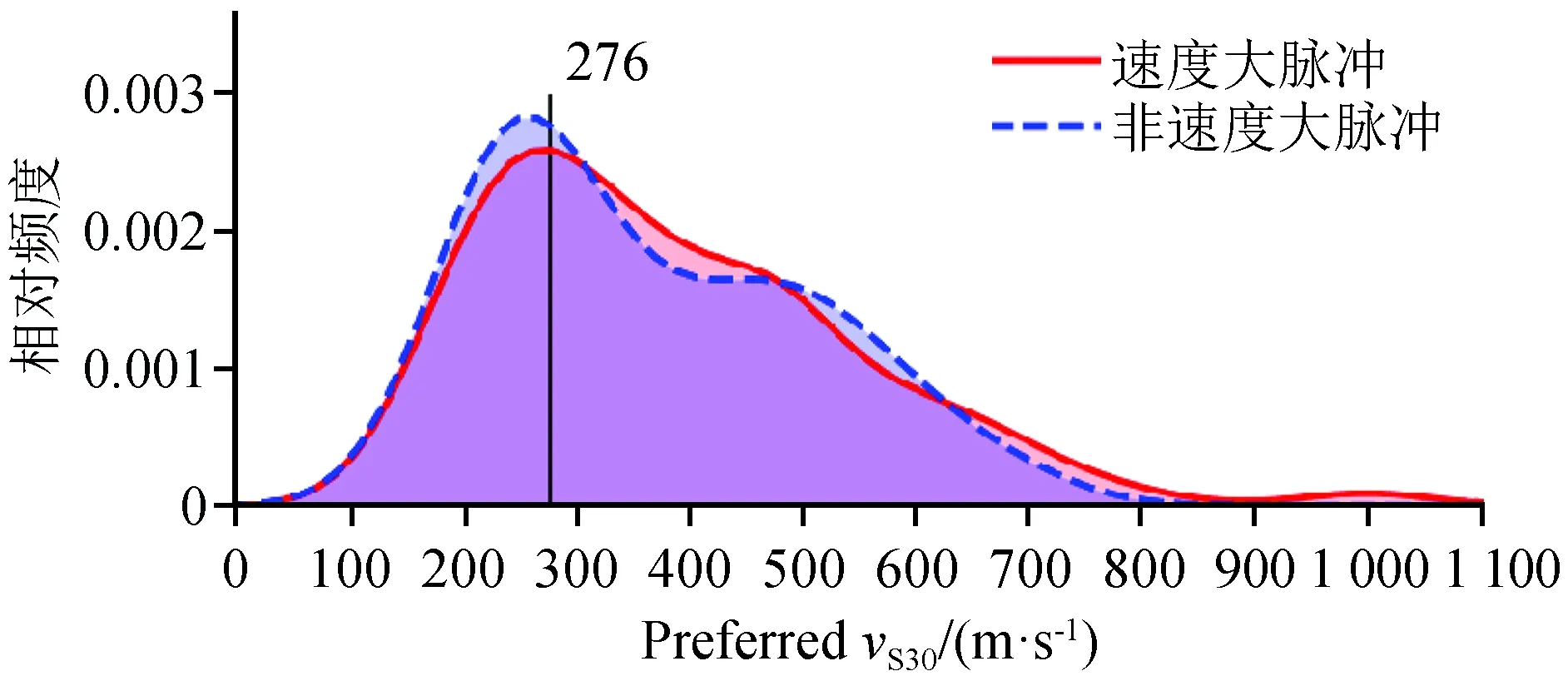
图2 场地条件与速度大脉冲关系Fig.2 The relationship between site conditions and big velocity pulse

震源深度是描述震源的最基本参数之一。震源深度越浅,地震传播到地面的能量越高[21]。图3展示了震源深度与速度大脉冲的关系。从图3可以看出,当震源深度较浅时(6～12 km),速度大脉冲的频度高于非速度大脉冲;在7 km处,速度大脉冲频度达到峰值,符合速度大脉冲具有高能量的特点。

已有研究用场地与断层走向的夹角来代表方向性效应,而方向性效应是引起速度大脉冲的主要原因之一[7]。图4展示了夹角与速度大脉冲之间的关系。从图 4可以看出在-78°和85°两个角度处,速度大脉冲频度出现峰值。在小角度范围内(-78°～30°,即断层破裂前方),速度大脉冲发生的频度大于非速度大脉冲;而在此范围外(即较大角度),没有显示出此种规律。

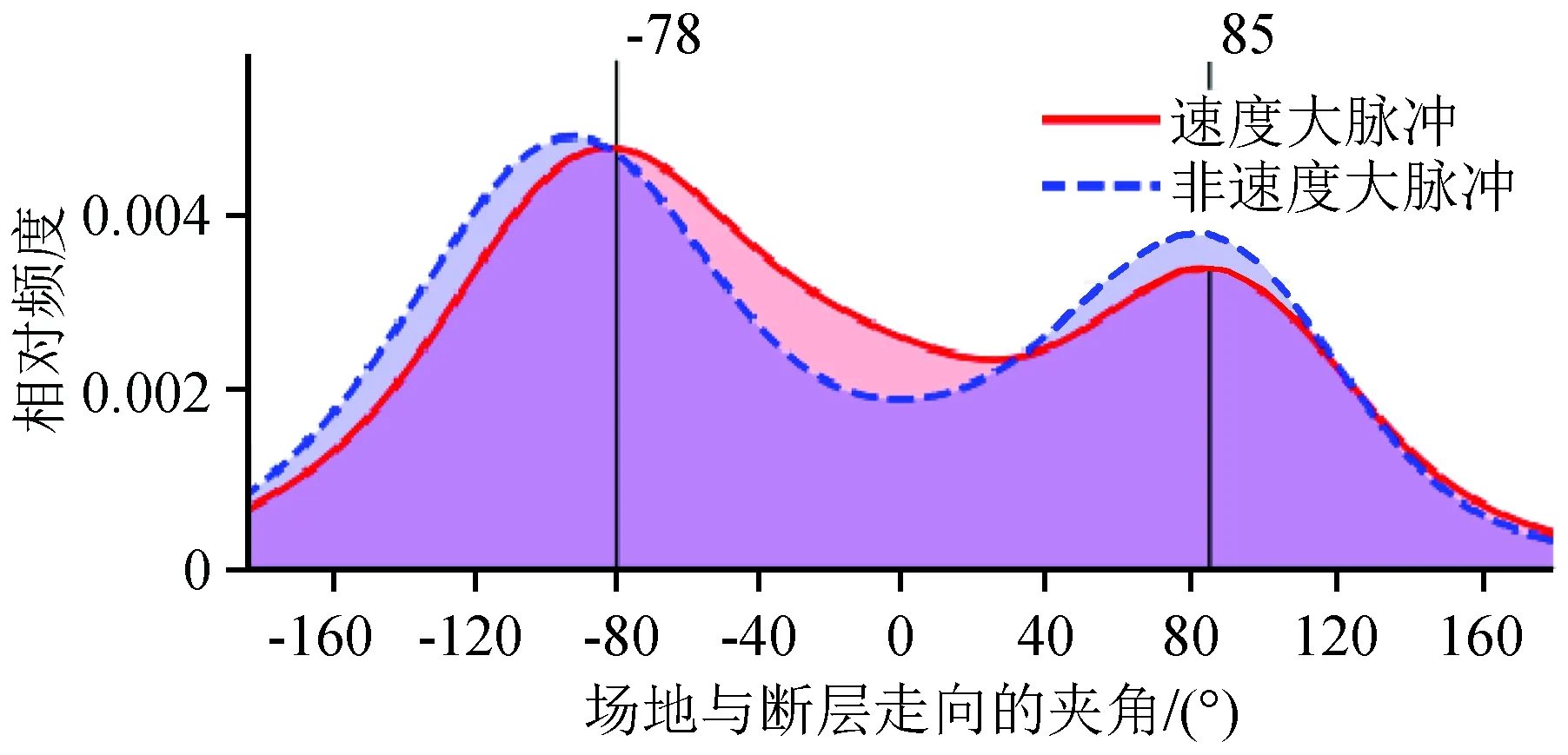
图4 场地与断层走向的夹角和速度大脉冲关系Fig.4 The relationship between Source to Site Azimuth and big velocity pulse

图5展示了震源距与速度大脉冲之间的关系。从图5可以看出,在震源距29 km处速度大脉冲频度出现峰值。虽然在小于50 km的范围内出现峰值,但是非速度脉冲的频度高于速度大脉冲;在50～130 km处速度大脉冲的频度大于非速度大脉冲,这一点在进行抗震设计时值得关注。

图5 震源距与速度大脉冲关系Fig.5 The relationship between HypD and big velocity pulse

图6展示了震中距与速度大脉冲之间的关系。从图6可以看出,在震中距25 km处,速度大脉冲频度出现峰值;在50～130 km处速度大脉冲的频度大于非速度大脉冲。因此,基于图5、6的分析,在距离潜在震中、潜在震源30 km内尽量不要建设重大工程,否则需要考虑速度大脉冲对结构的地震作用。

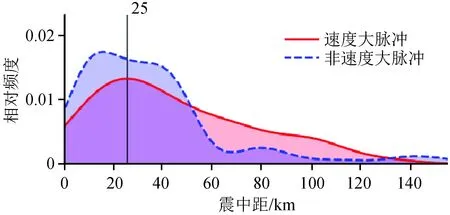
图6 震中距与速度大脉冲关系Fig.6 The relationship between EpiD and big velocity pulse

图7展示了乔纳布尔距离(即场地到破裂垂直投影的最短水平距离)与速度大脉冲之间的关系。从图7可以看出,在5 km处速度大脉冲频度出现峰值;在小于10 km和40～80 km的区域,速度大脉冲频度高于非速度大脉冲。

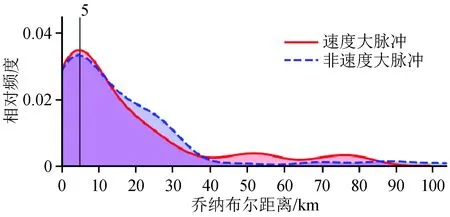
图7 乔纳布尔距离与速度大脉冲关系Fig.7 The relationship between Joyner-Boore Dist and big velocity pulse

图8展示了坎布尔距离(即场地距离破裂区发震部分最短距离)与速度大脉冲之间的关系。从图8可以看出,在8 km处速度大脉冲频度出现峰值;在小于6 km的区域,速度大脉冲频度高于非速度大脉冲;6～40 km范围内非速度大脉冲频度高于速度大脉冲;40～80 km速度大脉冲出现频度又高于非速度大脉冲。

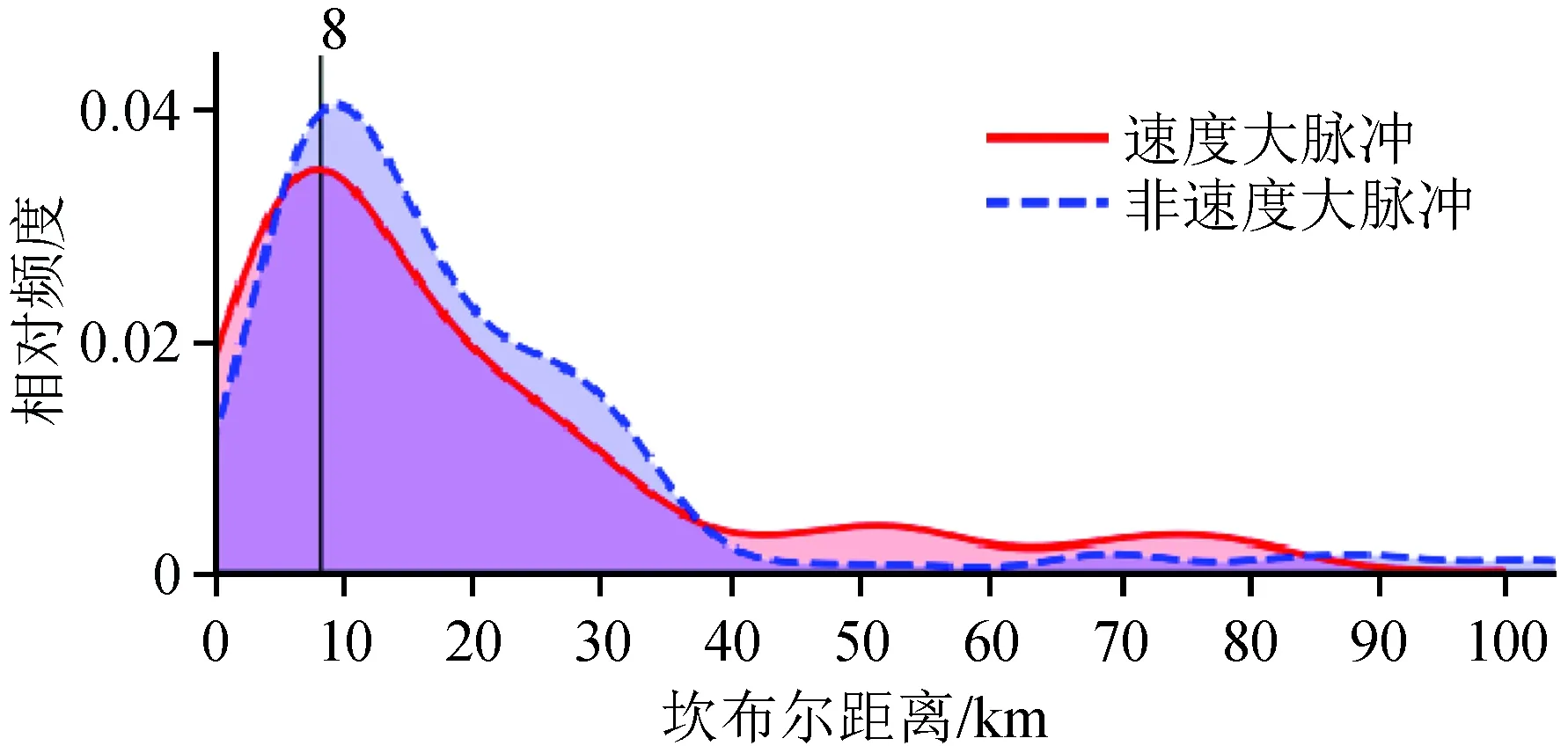
图8 坎布尔距离与速度大脉冲关系Fig.8 The relationship between Campbell R Dist and big velocity pulse

图9展示了均方根距离与速度大脉冲之间的关系。从图 9可以看出,在17 km处速度大脉冲频度出现峰值;小于15 km范围内速度脉冲频度高于非速度脉冲;15～63 km范围内非速度脉冲频度高于速度脉冲;63～110 km处速度大脉冲频度高于非速度大脉冲。

图9 均方根距离与速度大脉冲关系Fig.9 The relationship between RmsD and big velocity pulse

图10展示了场地距破裂区最近距离与速度大脉冲之间的关系。图 10表明,在7 km处速度大脉冲频度出现峰值;小于7 km范围内速度脉冲频度高于非速度脉冲;7～38km范围内非速度脉冲频度高于速度脉冲;38～85 km速度范围内大脉冲出现频度高于非速度大脉冲。

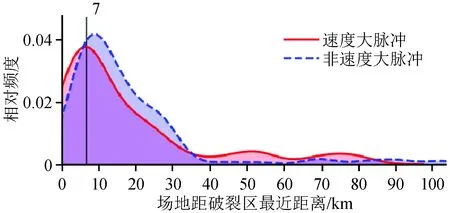
图10 场地距破裂区最近距离与速度大脉冲关系Fig.10 The relationship between ClstD and big velocity pulse

根据以上分析,本文认为距离潜在震中、潜在震源30 km范围内为速度大脉冲发生频度较高区域;在距离破裂区20 km范围内,速度大脉冲频度较高;另外在场地与断层走向的夹角较小范围内(即破裂前方),速度大脉冲频度较高。在以上区域内不要建设重大工程,否则需要考虑速度大脉冲对结构的特殊作用。重要工程选址要选基岩等场地条件较好的位置。不同因素与速度大脉冲之间均有关系,仅仅考虑单个因素对速度脉冲的影响是不全面的,因此在下一节中综合各个因素建立模型,并分析不同因素的敏感性。

4 建立模型

考虑到地震动的复杂性,影响速度大脉冲发生的因素较多。故本文对震源、传播路径、场地条件因素进行综合考虑,引入L1正则化方法,建立预测速度大脉冲地震动的逻辑回归模型。

4.1 基于L1正则化逻辑回归的速度大脉冲预测模型

利用Python语言进行数据处理,基于Scikit-Learn库建立逻辑回归模型[22]。为简化公式表达形式,用符号代表各个因素,各个符号含义如表3所列。利用289条记录进行回归分析、验证,得出速度大脉冲预测公式:

(7)

表3 回归公式中符号含义Table 3 Meaning of symbols in regression formula

式(7)是经过L1正则化逻辑回归建立的,AUC值为0.76,未经过L1正则化的AUC值为0.72,可见L1正则化后,模型性能有了较大提升。AUC值为0.76表明该模型具有较好的性能。P为速度大脉冲发生的可能性,本文规定,若P≥0.5,则记为1(发生速度大脉冲),否则记为0(非速度大脉冲)。

式(7)由实测资料分析建立,考虑了地震的不确定性和各影响因素的耦合作用,通过相应的参数预测速度大脉冲的发生。因为该模型是基于一定的数据建立的,故本文给出的速度大脉冲预测公式适用条件是:10个变量的分布范围必须符合本文分析数据的分布规律。

4.2 不同正则化系数对模型的影响

式(6)中,∂参数主要控制正则化强弱,参数值越大越容易过拟合,参数值越小越容易欠拟合,因此选择合适的正则化参数对模型性能有较大影响。本文探究了不同正则化参数对模型的影响,主要考虑对AUC值的影响,结果见图 11。由图11可知,当∂为0.5时,AUC值为0.76,性能最优。因此本文中选用正则化系数0.5建立如式(7)所示的速度大脉冲预测模型。

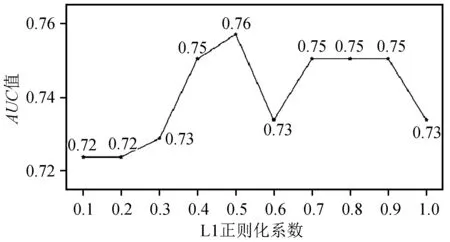
图11 不同正则化系数对模型结果的影响 Fig.11 The influence of different regularization coefficients on model results

4.3 敏感性分析

为进一步评估每一个因素对模型[式(7)]的影响,迭代10次,每次迭代删除一个因素并给出每个模型的AUC值,进而判断模型对不同因素的敏感性。从图12中可以看出,模型对不同因素的敏感性由大到小依次为:x1、x6、x2&x4、x0&x9、x7&x8、x3&x5。由敏感性分析可知,该模型最敏感因素为破裂区的距离，这符合发震断层带状破裂过程对地震动的影响规律。

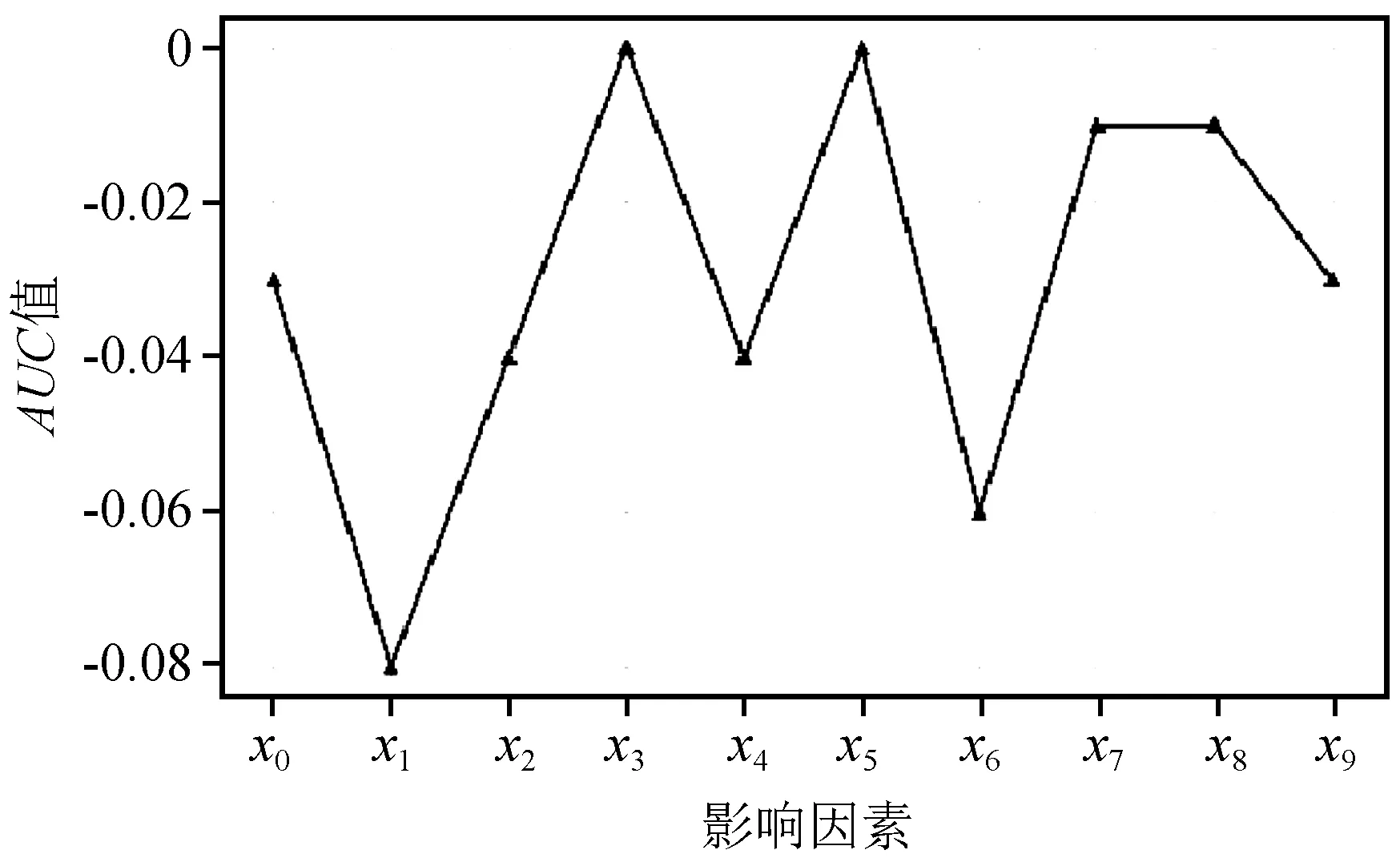
图12 敏感性分析Fig.12 Sensitivity analysis

删除最敏感的影响因素后,预测模型的AUC值仍旧在0.68,能满足速度大脉冲的预测。这也进一步证明了当出现数据信息缺少的情况时,预测模型仍然有较好的预测准确性,表明该模型具有灵活的适用性。

5 案例分析

2008年四川盆地西缘发生了汶川MS8.0地震,中国数据强震动观测台网获取到大量近断层加速度记录,其中许多近场记录具有明显的速度大脉冲特征[23-24]。这些强震记录为本文案例分析提供了非常宝贵的资料。选取符合本文回归分析数据分布的35条地震数据信息对本文模型进行验证,地震信息列于表4。由表4可知坎布尔距离大量缺失,本文训练的最优模型无法适用,故使用如式(8)所示的删除坎布尔距离信息后的速度大脉冲预测模型(AUC值为0.72)。

(8)

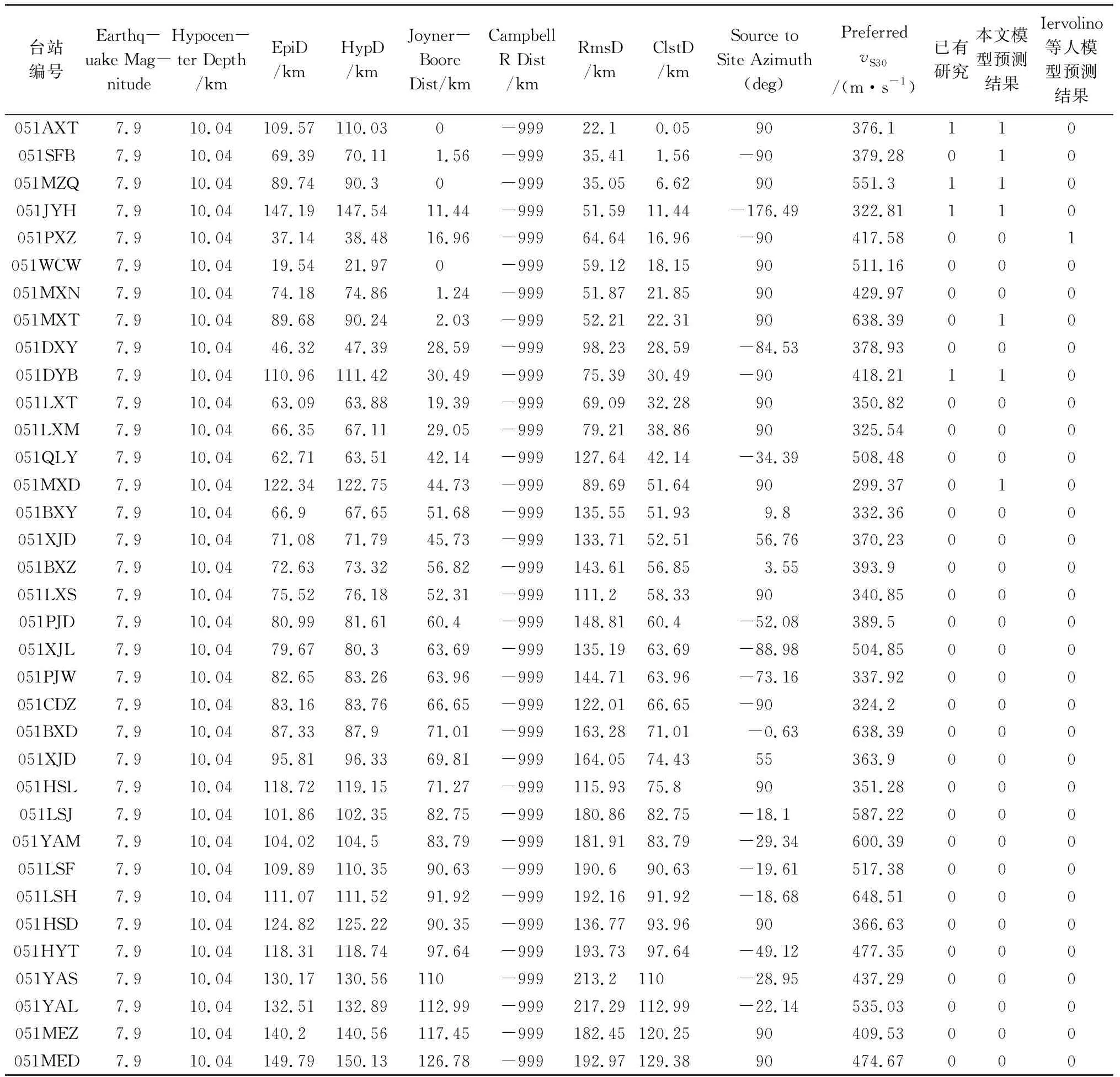
表4 汶川强地震动信息及预测结果Table 4 Strong ground motion information of Wenchuan earthquake and prediction results

模型预测结果列于表4。由表4可知,35条记录中3条记录(051SFB、051MXT、051MXD)预测错误,32条记录预测正确,但其中速度大脉冲全部预测正确,准确率较高。安县塔水台(051AXT)记录的地震动因为晚到脉冲被部分学者排除，但是该地震动中也包含速度大脉冲[25]。为进一步验证本文速度大脉冲预测模型的准确性,与Iervolino等[13]的预测模型进行对比。由于汶川地震属于逆冲-走滑型地震[26],故选取如式(9)所示的最优走滑型速度大脉冲预测模型:

(9)

式中:R,S,θ分别为场地到断层的距离，场地在断层投影与震中的距离，以及站点与震中连线和断层的夹角。

式(9)的预测结果同样列于表4。由表4可知，35条记录中30条预测正确。通过对比可知,本文模型相较于已有模型,预测的准确率有了一定的提高,表明本文提出的模型具有较高的有效性以及较好的泛化能力。

6 结论

科学预测速度大脉冲是否发生以及不同因素对速度大脉冲发生的影响,对于概率危险性分析和减轻地震灾害有重要的作用。本文从美国NGA数据库中选取了315条地震记录,并通过后期数据处理得到289条记录用于研究。通过地震记录的相对频度分析给出了不同因素对速度脉冲的影响,总结了不同因素影响的规律和重点。然后,利用正则化逻辑回归方法建立了速度大脉冲预测模型,并对正则化系数对模型的影响以及模型对不同因素的敏感性进行了对比分析。最后,利用35条汶川地震实测数据对本研究模型进行了验证，得到如下结论：

(1) 距离潜在震中、潜在震源30 km范围内为速度大脉冲发生较多区域。在距离破裂区20 km范围内及在场地与断层走向的夹角较小范围内(即破裂前方),速度大脉冲频度较高。在以上区域内不要建设重大工程,否则需要考虑速度大脉冲对结构的特殊作用。场地条件对于包含速度大脉动的地震动产生有很显著的影响,因此重大工程选址时要选择基岩等地质条件较好的场地位置。

(2) 基于L1正则化逻辑回归方法建立了速度大脉冲预测模型。模型的AUC值为0.76,表明模型有较好的预测能力。分析了正则化系数对于预测模型的影响,得到了适用于该预测模型的正则化系数取值为0.5。分析了预测模型中不同因素对于模型的敏感程度,对比发现删除破裂区距离后,模型的AUC值会产生很大的影响,模型预测的准确程度大幅度降低。故在预测模型中,破裂区距离是建立模型的关键性因素。

(3) 选用汶川地震实测数据进行模型验证,并与现有预测模型的预测效果进行对比,结果表明本文所提预测模型的有效性更好。