球柱壳耐压舱体极限承载力研究

张洪彬，徐会希

(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 110016; 2.中国科学院 机器人与智能制造创新研究院，辽宁 沈阳 110169; 3.辽宁省水下机器人重点实验室，辽宁 沈阳 110169)

耐压作为深潜技术的重要环节，是决定水下机器人[1-2]下潜深度的关键。而大压力条件下的耐压舱体结构设计，一直是直接关乎水下机器人安全性与总体指标的重要研究内容。但是单纯依赖线性静强度失效计算，即假设耐压舱体结构不会发生失稳破坏，远远不能满足设计安全性要求。经验表明，大深度钛合金薄壳及中厚壳类耐压舱体结构，其破坏形式往往是先发生失稳失效，即极限承载力是决定水下机器人大深度下潜的核心指标。

有限元的特征值屈曲分析只能计算出理想结构的临界失稳载荷，结果非保守。针对球壳结构，传统经验公式的计算误差一般可以比试验值大3倍左右，参考价值更小。围绕极限承载力的计算，国内外已有一些科研成果产出[3-9]，但目前的研究成果主要集中在针对载人潜水器的球壳体结构，针对无人潜水器常用的球壳封盖加圆柱形耐压壳体结构的极限承载力研究少之又少。

文中研究基于有限元理论的非线性屈曲分析方法，为了提升计算的准确性，首先采用装配体整体建模策略，搭建复合屈曲失稳的初始受力模型。然后在同时考虑材料非线性、几何非线性、接触非线性等方面因素的条件下，评估承压结构的最大极限承载力。最后针对初始缺陷导入尺度这一关键参数展开深入研究，结合试验结果验证，确定柱形耐压壳体结构的初始缺陷导入尺度参数，为未来的耐压舱体结构设计、计算分析及压力试验提供试验指导与技术支撑。

1 传统经验公式计算方法

1.1 耐压球壳的经典失稳公式

早在1915年，R.Zoelly就基于小变形假设，导出受外压的耐压球壳经典失稳公式[10]，这是最早的稳定性校核公式。

(1)

其中，pE为临界失稳压力，E为弹性模量，μ为泊松比，t为球壳厚度，R为球壳中面半径。此经典公式包含4个基本假设：1)对材料各向均匀同性；2)有完善的几何球形；3)无初始内部应力；4)满足线弹性本构方程。

该经验公式的局限性和误差来源有：几何形状的完善只能是理想化球壳结构，无法考虑结构初始缺陷和结合非线性的影响；基于线弹性的基本假设，忽略了材料和几何非线性及内部残余应力等因素，使得分析过程过于简化。

当球形壳体承受均匀外压时，球壳的计算应力有：

(2)

其中，p为外压力。

将式(2)代入式(1)，临界失稳应力有：

(3)

1.2 BERCH公式

在经典公式的基础上，结合许多学者的后续实践，又有新的经验公式产生。代表性的有BERCH公式：

(4)

其中，σs为屈服强度，pcr为壳体的临界压力。

1.3 德川公式

基于20面体近似球壳推导的德川公式为:

(5)

其中，D为球壳直径。

将理论模型与试验模型进一步结合后，根据厚度直径比的不同具体有：

(6)

(7)

上述经验公式都在经典理论的基础上，结合模型的试验结果进行一定程度的优化，式(4)引入并适当考虑了材料的特性，式(6)和(7)针对厚径比进一步将公式详细区分，但是都没有考虑初始结构缺陷对于非线性稳定性的影响。

1.4 卡门—钱学森公式

考虑球壳微小变形的能量法求解得到卡门—钱学森公式，公式考虑了结构初始缺陷对于结构稳定性的影响。

(8)

1.5 美国海军泰勒水池耐压壳设计公式

美国海军泰勒水池耐压壳设计公式为:

(9)

1.6 俄罗斯深海潜水器耐压壳体的临界压力公式

俄罗斯深海潜水器耐压壳体的临界压力公式为:

(10)

1.7 经验公式总结

已有相关学者对于上述经验公式进行研究，对上述部分经验公式的计算结果进行对比评价，这里不做深入分析。只给出基本结论：经典计算公式和部分经验公式，由于没有考虑材料非线性、几何非线性、接触非线性和初始几何缺陷诸多因素中的一种或者多种，使得计算结果误差较大，工程指导意义有限。

美国海军泰勒水池耐压壳设计公式和俄罗斯深海潜水器耐压壳体的临界压力公式，充分考虑结构局部缺陷和材料特性对于最大极限承载力的影响，计算公式经过大量试验数据修正，有较强的参考价值。但是由于试验和公式都是基于球壳或者类球壳结构完成的，同时试验所用材料在漫长的发展过程中其力学性能参数也有较大差异，所以针对钛合金材料广泛采用的圆柱筒体加球壳封盖式承压结构，经验公式计算方法的指导价值有很大的局限性。

2 非线性屈曲分析流程

2.1 不同类型缺陷结构分析流程

非线性屈曲分析，可以细分为确定性缺陷模型分析方法和非确定性缺陷模型分析方法两种。针对两种模型建立分析流程如图1所示。其中确定性缺陷模型分析方法针对已知可测量的缺陷模型，进行三维缺陷建模后开展极限承载力分析；非确定性缺陷模型分析方法针对缺陷无法精确测定的几何结构，借助特征值屈曲的模态阵型进行缺陷导入后分析。

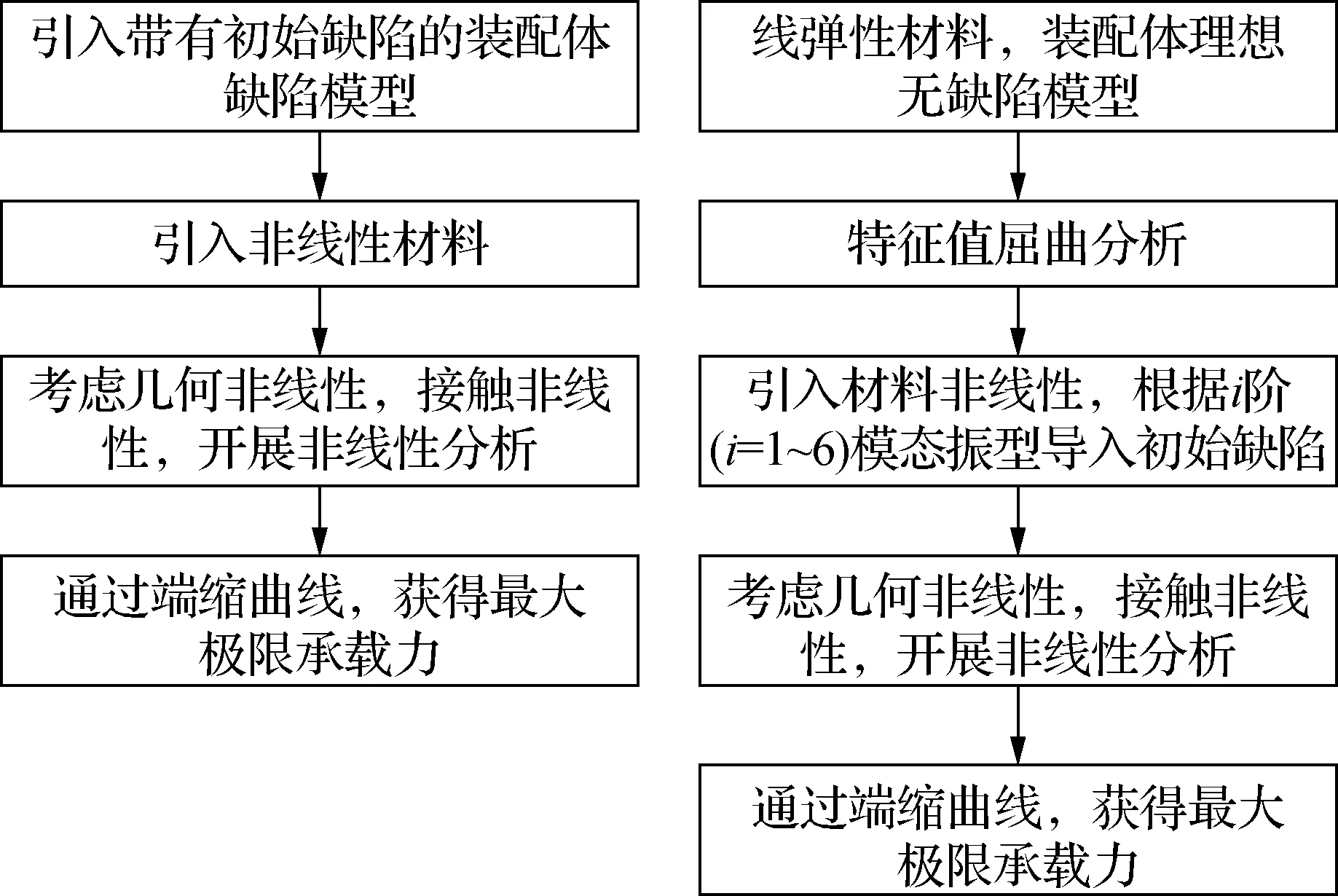
图1 非线性屈曲分析流程

2.2 材料非线性特性

极限承载力分析技术需要充分考虑材料的塑性应力应变特性，通过力学试验测定钛合金TC4棒料的材料应力应变曲线和塑性应力应变曲线分别如图2和3所示。铝合金7075棒料的塑性应力应变曲线如图4所示。

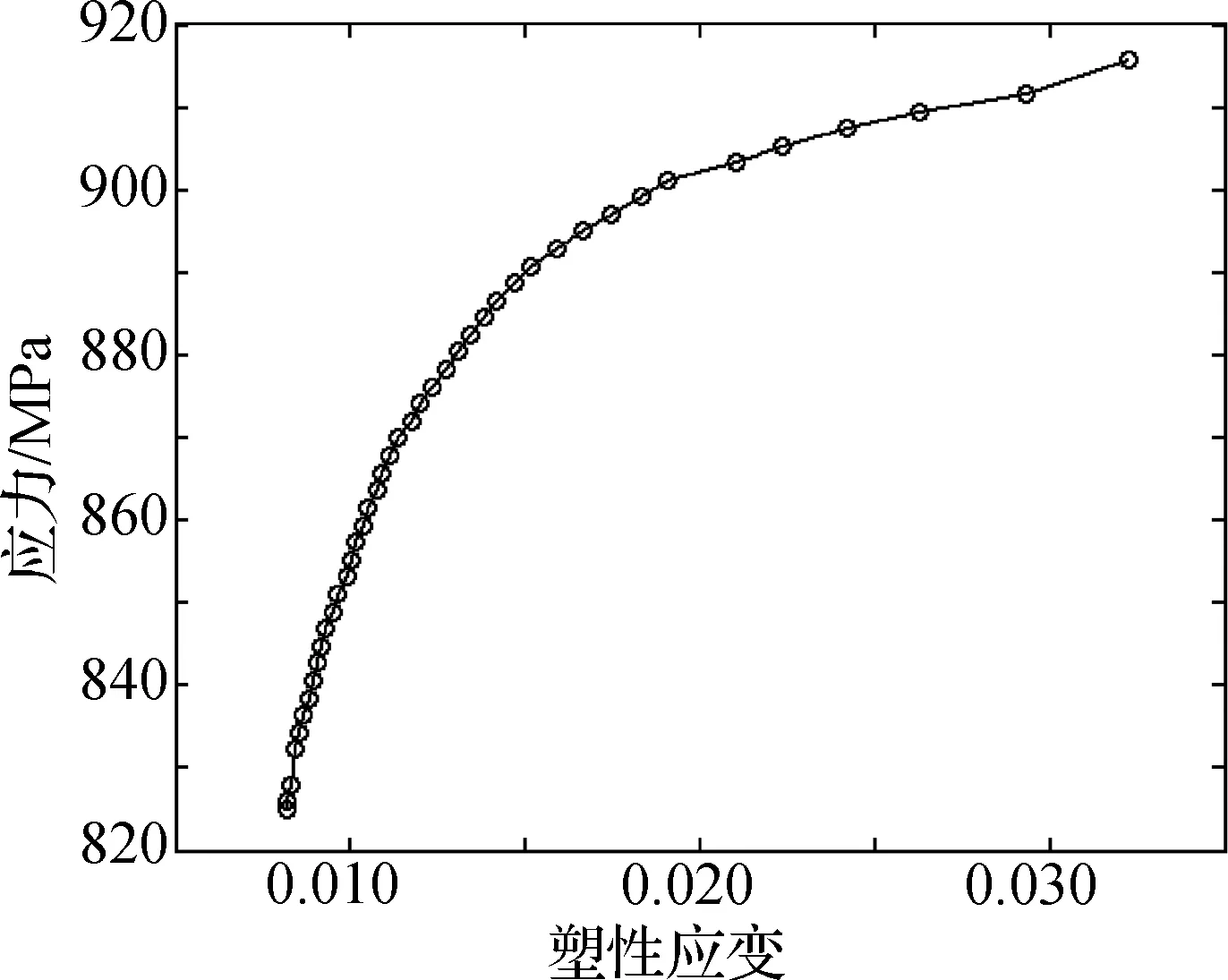
图3 钛合金TC4单轴拉伸试验塑性应力—应变曲线

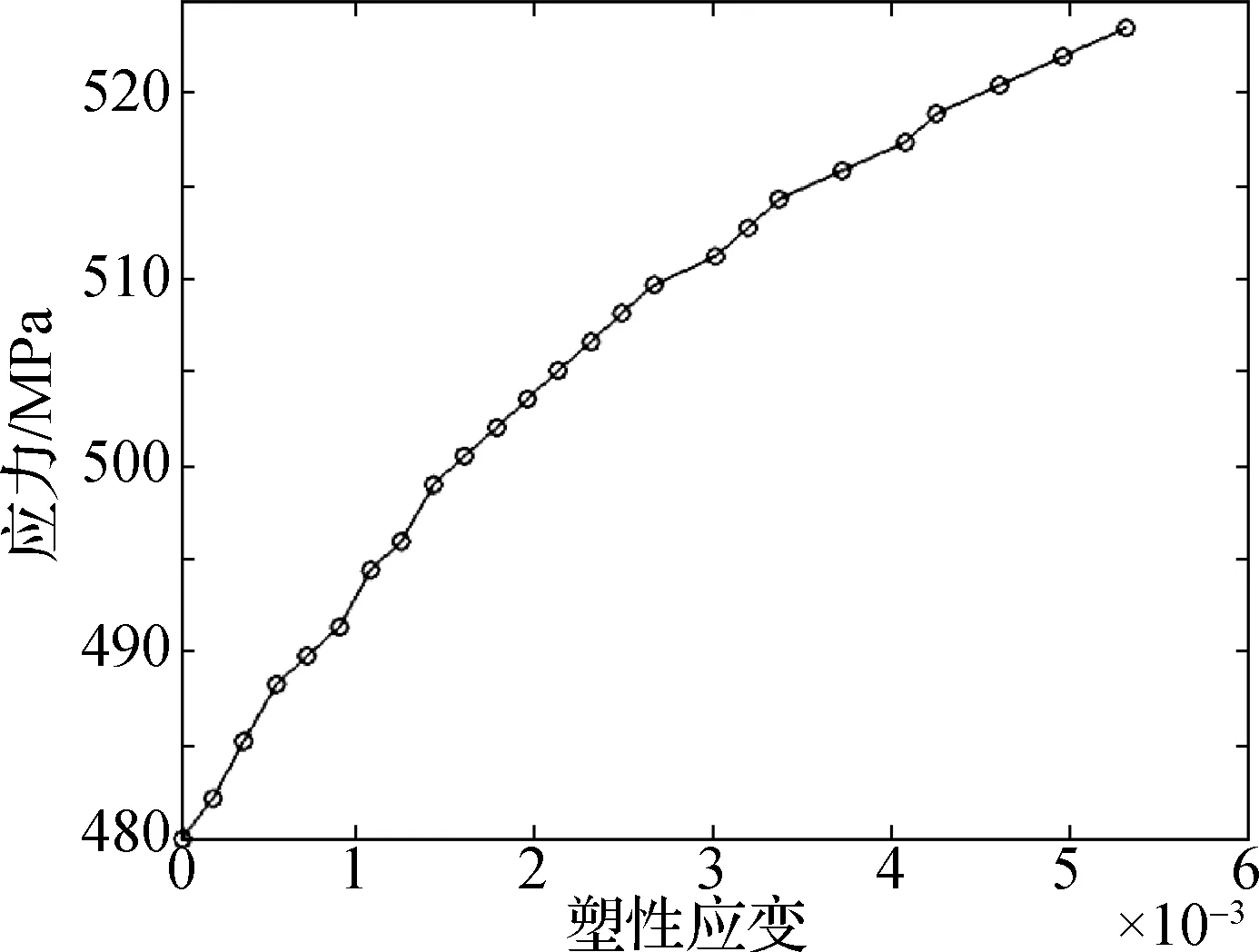
图4 铝合金7075单轴拉伸试验塑性应力—应变曲线

2.3 几何非线性特性

当结构的变形使体系的受力发生显著变化，以至不能采用线性体系的分析方法时就称为几何非线性，即力与位移不再是直线关系。常见分类有大位移小应变问题、大位移大应变问题、大转角问题。直观理解为当结构的位移相对于结构本体的尺度不再是高阶小量时，需要充分考虑几何非线性问题。

2.4 接触非线性特性

接触是状态改变的非线性，系统刚度随接触状态的变化而实时更新，是一个高度非线性的过程。对于研究的球壳封盖加圆柱形耐压壳体的耐压舱体结构，半球壳与圆柱筒体在接触面之间力的精确传递也是影响全局结构极限承载力的关键环节。同时由于球壳与圆柱壳体耐压能力的差别，等壁厚条件下交界面上的圆柱筒体边缘刚度远远小于球壳体边缘刚度。所以如果采用零件一体化建模或者共用节点的方式处理，会使得球壳边界将圆柱壳体边界进一步强化，边界传力不精确，计算结果误差偏大。

所以充分考虑耐压舱体密封形式及其深海环境下的实际工作受力状态，采用装配体整体建模策略，结合面采用非线性摩擦接触建模，将力精确传递，同时充分考虑结合面上不同零件结构刚度的差异。但接触的引入往往会使得极限承载力的求解收敛变得异常困难，所以文中引入稳定能这一求解技术解决这个问题，使得这一超强非线性的极限承载力分析能够排除数值不稳定的失稳点，获得物理不稳定的数值解。

3 初始缺陷的确定

3.1 非确定性缺陷模型

针对非确定性缺陷模型，此类缺陷主要针对设计阶段的结构，以及无法测定缺陷大小和尺寸的结构。此类缺陷的引入需要通过线性屈曲分析求解出屈曲模态，计算中的阵型需要选择对于结构最为不利的一阶阵型，该阶阵型的形态即为在此结构振动方向上刚度最弱，最容易发生失效的形态。对于球壳类结构，因其结构形式具有先天的高抗压能力，经验的屈曲模态常取第一阶阵型。对于圆柱筒体类结构，需要通过输出前6阶模态阵型后进行人工选择，挑选最不利的一阶阵型进行导入。

由于屈曲模态阵型的数学含义只是一个无量纲的归一化特征向量，即没有表征缺陷大小的含义，所以需要将阵型向量的最大振幅值放大一定的倍数。这个倍数叫做屈曲形状导入因子，其具有长度上的量纲，大小为屈曲形状缺陷(长度量纲)与屈曲模态阵型最大振幅(无量纲)的比值。

针对屈曲形状缺陷的取值，不同的文献资料有所不同。这里只列举相关的参考标准及具体的屈曲形状缺陷取值。以某型无人潜水器的耐压舱耐压筒体为例进行详细研究，针对不同的屈曲形状缺陷0.115 mm、0.274 2 mm、0.6 mm分别计算，并给出最大极限承载力。

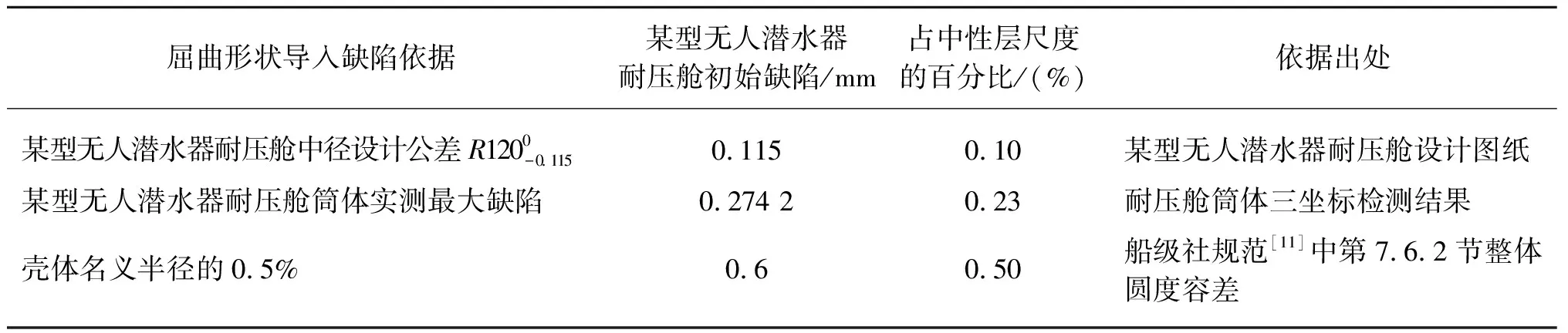
表1 屈曲形状缺陷导入值

3.2 非线性屈曲有限元模型网格要求

非线性屈曲分析，是一项要考虑材料非线性、几何非线性和边界(接触)非线性要素，同时加入几何初始缺陷的高度非线性、复杂有限元分析，这样的高级分析计算需要高质量的网格划分技术支撑。具体的单元选择与网格质量要求为：

1)采用多节点高精度单元对结构进行计算；

2)单元类型壳体单元尽量选择四边形壳体单元离散，实体单元尽量选择六面体单元离散；

3)网格质量尽量划分到0.7以上，最好不要低于0.5，如果存在局部不规则特征，可以尝试局部细化手段处理。

4 非线性屈曲具体算例校核

首先针对带有确定性缺陷的厚壳耐压舱体结构进行极限承载力分析，针对某型潜水器的铝合金7075材质厚壳耐压舱体，对其进行表面缺陷尺寸的测绘，将此测绘的缺陷建模埋入到几何模型中，进行极限承载力分析；将缺陷去除，即使用理想无缺陷厚壳模型进行极限承载力分析；再将计算结果与基于船级社标准[11]缺陷容差模型的最大极限承载力对比分析。针对某型潜水器的薄壳钛合金材质耐压舱体模型，不同缺陷尺度的导入标准，分别进行非确定性缺陷最大极限承载力分析。计算得出相应的稳定性安全系数，对相应的耐压舱安全性进行评估。

4.1 确定性缺陷算例

4.1.1 某型潜水器点蚀缺陷厚壳耐压舱极限承载力校核

建立某型潜水器耐压筒体模型，此耐压舱圆柱筒体20 mm等壁厚，球盖顶部最薄厚度10.2 mm。预埋缺陷尺寸为R=5.7 mm，深度2.83 mm，两个位于中心位置，另外一个沿母线方向80 mm对称布置，具体如图5所示，图中为二分之一对称建模，只显示两个缺陷凹坑。

图5 确定性缺陷三维建模

所加边界约束条件如图6所示，约束对称面上的x(法向)位移和球盖顶部的切平面内自由度，即释放轴向移动自由度。耐压舱体接触面施加摩擦系数0.1的摩擦约束。后续章节边界条件与本章节相同，不做赘述。极限承载载荷为89 MPa。

图6 边界条件

4.1.2 某型潜水器无蚀缺陷厚壳耐压舱极限承载力校核

使用4.1.1节中去除缺陷后的模型，即建立无缺陷理想化耐压舱有限元模型，按照确定性缺陷的极限承载力流程计算，获得最大极限承载力为88.8 MPa，与带有小尺度点蚀凹坑缺陷的耐压舱体结构最大极限承载力相差不大。

4.1.3 非确定性缺陷厚壳耐压舱体结构极限承载力分析

使用非确定性缺陷模型屈曲计算方法，执行船级社规范[11]要求，缺陷尺度为中性层半径的0.5%，中性层半径为125 mm，导入缺陷为0.625 mm。进一步对比评估0.5%的整体模态屈曲阵型缺陷对于某型耐压舱体最大极限承载力的影响情况。经过计算获得临界失稳压力为79 MPa。

4.1.4 小结

1)带有2.83 mm深度的确定性缺陷厚壳耐压舱体极限承载力为89 MPa，理想无缺陷某型厚壳耐压舱体临界失稳压力为88.8 MPa，由此可得该尺度点蚀类缺陷对于厚壳结构的极限承载力影响微乎其微，工程上可以忽略处理。

2)真球度和圆柱度等形状缺陷和耐压壳体厚度对于极限承载的影响权重较高。

4.2 非确定性缺陷算例

针对某型薄壳耐压舱体，分别进行屈曲形状导入缺陷为0.115 mm、0.274 2 mm、0.6 mm 时的最大极限承载力计算。线性屈曲最危险阵型云图如图7所示。

图7 耐压舱体最危险线性屈曲阵型云图

由图7可知屈曲模态阵型最大振幅为1.000 3，所以屈曲缺陷导入因子为0.115 mm/1.000 3=0.115 0 mm、0.274 2 mm/1.000 3=0.274 1 mm、0.6 mm/1.000 3=0.599 8 mm。将会以此导入因子借助软件命令流将模态缺陷输入到计算模型中。不同模态缺陷导入尺度与极限承载力的关系如表2所示。

表2 模态缺陷导入尺度与极限承载力关系

为充分验证极限承载力计算的准确性，在中国科学院沈阳自动化研究所水下试验室开展水压爆破试验，将上述经三坐标检测的耐压舱体放入压力罐内开展爆破试验，在缓慢升压至54 MPa后保压约5 min时，发生耐压舱舱体的压溃碎裂、球壳的变形、法兰的断裂，如图8所示。

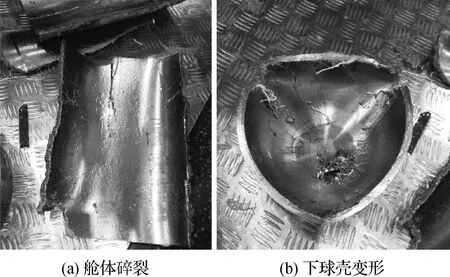
图8 某型耐压舱压力试验后照片

舱体的三坐标检测缺陷最大值检测结果详见表1第二组数据，实测的缺陷参数宏观表现为整体的不圆度，最大值为舱体结构的0.23%，这与有限元中的模态缺陷定义契合。因此，通过水压爆破试验，验证了极限承载力计算结果准确可靠。

5 结 语

在装配体整体建模策略的基础上，同时考虑材料非线性、几何非线性、接触非线性等方面因素，评估承压结构的最大极限承载力。并针对初始缺陷导入尺度这一关键参数展开深入研究，研究得出不同类型的缺陷对承压结构的削弱有所不同。最后给出缺陷导入参数建议值，并对球柱壳体耐压舱的结构分析提出要求。

1)带有2.83 mm深度的确定性缺陷厚壳耐压舱体极限承载力为89 MPa，理想无缺陷某型厚壳耐压舱体临界失稳压力为88.8 MPa，二者相差0.225%，因含有确定性缺陷的舱体结构无法全局采用结构化网格，由此引入一定的数值计算误差，但计算结果差异较小。由此可得该尺度点蚀缺陷对于厚壳结构的极限承载力影响较小，工程上可以忽略处理。

2)真球度和圆柱度等形状缺陷和耐压壳体厚度对于极限承载的影响权重较高。

3)针对无人潜水器的球壳封盖加圆柱形耐压壳体结构，0.5%的缺陷尺度对于结构的稳定性削弱过大，存在过安全的问题，对于耐压舱体数量众多的无人潜水器而言，过大的质量总体指标也无法接受。

4)基于研究成果，球壳封盖加圆柱形耐压壳体结构，缺陷导入尺度为0.23%，该缺陷导入尺度即为现有结构临界失稳极限缺陷值。

5)钛合金类薄壳耐压舱体结构分析的非线性屈曲分析重要性远远大于静强度失效校核分析。所以一个严谨的强度校核分析必须是静强度失效校核与非线性屈曲分析两相结合。