含约束和通信时滞的多智能体系统包含控制
2022-04-02侯海良
张 旺,侯海良
(湖南人文科技学院 信息学院,湖南 娄底 417000)
0 引 言
近几年来,随着人工智能的普及,多智能体系统协同控制受到了广泛关注。包含控制作为其中一个重要的分支,在实际中有着广泛的应用前景,如无人机护航编队、多机器人协同避障等。文献[1]提出了一种走走停停的控制策略,解决了固定无向通信拓扑下的包含问题,并首次明确了包含控制的目标是将一组跟随者智能体驱动到由领导者构成的凸区域内。文献[2-4]研究了固定网络下的包含控制问题。文献[5-6]研究了无向切换网络的包含控制问题。文献[7]分别研究了领导者运动和静止两种情况下有向切换网络的包含控制问题。以上研究均未考虑时滞问题,实际上由于信息采集、传输、处理等需要时间,时滞问题不可避免,必定会对控制产生影响。文献[8-11]研究了固定网络下考虑通信时滞的包含控制问题。文献[12]提出了一种基于投影的非线性包含控制算法,解决了有向切换网络中存在通信时滞的包含控制问题。文献[13]分别针对一阶和二阶系统提出了两种不同的包含控制算法,解决了有向切换网络中存在通信时滞的包含控制问题。文献[14]将文献[13]的研究内容拓展到离散系统中,并改进了包含控制算法。
上述研究[1-14]假定智能体的控制输入和状态可以任意变化。但在实际应用中,受物理条件的限制,智能体运动不可避免地要受到一些约束,如受能耗影响,机器人的速度只可能在一定范围内变化。文献[15-16]研究了受约束的多智能体系统控制问题,其所受约束为凸性,这往往与实际不符。例如舰艇在水中可以朝各个方向运动,速度最快的方向为舰艇的前进方向,各个方向的运动速度形成了一个非凸区域。在文献[15-16]研究的基础上,文献[17-19]进一步研究了受非凸速度约束以及非凸输入约束的控制问题。需要强调的是文献[15-19]都是研究多智能体系统一致性问题。文献[20]提出了一种基于投影的非线性包含控制算法,解决了连续系统输入受约束的包含控制问题。
文献[1-20]中提到的系统均是离散的或者连续的。在实际应用中通常智能体使用的控制器为计算机或微处理器,智能体的状态信息需要经过采样后传输给邻居智能体,且在某些特定的环境中只能获得采样数据。与连续系统相比,采样系统只需要对采样数据进行传输,减少了通信能耗。与离散系统相比,采样系统不需要将控制系统做离散化处理,且进行周期采样得到的数据便于处理。文献[21-22]研究了固定网络下采样系统的包含控制问题。文献[23]研究了切换网络和通信时滞的采样系统包含控制问题,但都没有考虑采样系统的约束问题。
该研究受输入约束和通信时滞影响的采样多智能体系统包含控制问题,提出了一种基于投影的分布式协调控制算法。首先针对跟随者智能体设计了一种基于投影的非线性包含控制算法,将所有跟随者智能体到凸包的最大距离定义为李雅普诺夫函数,根据李雅普诺夫稳定性理论证明只要每个跟随者智能体能直接或间接至少收到一个领导者的信息,受限包含控制问题就能解决。最后通过数字案例证明了该包含控制方法的有效性。
1 图论与预备知识
G(ν,ε,A)表示含n个节点的有向图,ε⊆{(i,j):i,j∈ν}表示边集,ν={1,2,…,n}表示节点集,A=[aij]∈n×n表示邻接矩阵的权值。aij≥0表示边的权值,(j,i)∈ε表示节点i能接收到节点j接收的消息,当(j,i)∈ε且i≠j时有aij>0,否则aij=0。在有向图G(ν,ε,A)中,有向路径由有序边序列(i1,i2),(i2,i3),…构成,其中(ij,ij+1)∈ν。多个有向图G1,G2,…,GN的并集为GM,GM仍是一个有向图,且GM的边集等于全部有向图Gj,j=1,2,…,M边集的并集。+表示所有正整数的集合,g表示g维实列向量的集合。‖x‖表示向量x的标准欧几里得范数。PY(x)表示x在封闭区域Y上的投影,定义为:
引理1:设凸集Q∈r为非空封闭凸集,γi∈r表示任意向量,如果ai≥0,i=(1,2,…,n)满足那么有
定义1:设Ui⊆r是一个有界的非空封闭集合,当x=0时,SUi(0)=0,当x≠0时,则将SUi(x)称为约束算子。此外其中均是正常数。
约束算子SUi(x)的物理意义是找到与矢量x方向相同的矢量SUi(x)使其满足‖SUi(x)‖≤‖x‖,并且对于任意θ∈[0,1],都满足θSUi(x)∈Ui。值得指出的是,该约束算子不要求Ui为凸性(如图1所示)。
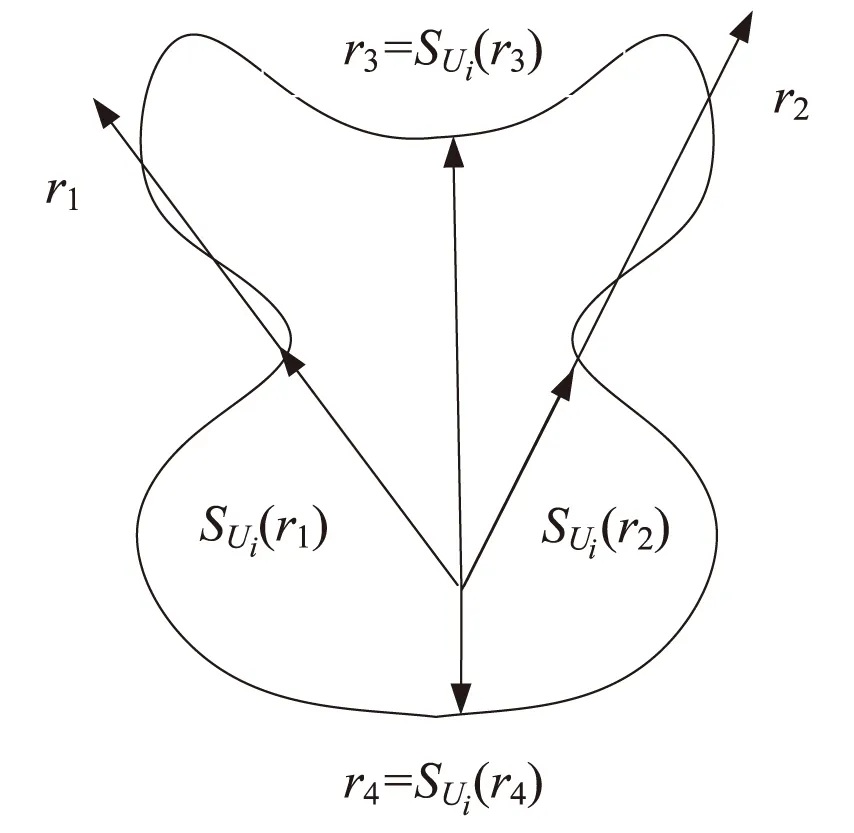
图1 约束算子示意图
2 问题提出及系统设计
设多智能体系统由l+n个智能体组成,包括l个领导者智能体(下文简称领导者)和n个跟随者智能体(下文简称跟随者),F={1,2,…,n}表示跟随者集合,L={n+1,n+2,…,n+l}表示领导者集合。xi(k)∈r表示跟随者在kT时刻的位置,ui(k)∈r表示跟随者在kT时刻的控制输入。T>0表示采样周期,为了简便起见,后面统一用k表示kT。所有领导者和跟随者构成了通信拓扑图G(ν,ε,A)的节点集。

xi(k+1)=xi(k)+SUi(ui(k))T
(1)
考虑通信时滞影响,设计包含控制算法为:
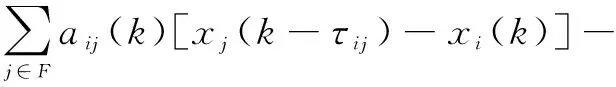
ci(k)[xi(k)-PYi(k)(xi(k))]
(2)
式中,τij(i≠j)为跟随者i与j之间的通信时滞,τij<τmax,τmax为最大通信时滞。如果aij>0,假设aij>λ,λ为一个正常数。跟随者i如果能至少接收到一个领导者的信息,则有ci(k)>0,否则ci(k)=0。同样假设如果ci(k)>0,则ci(k)≥λ。
3 稳定性分析
为了便于后续分析,定义一个新的变量hi(k),当k≥0时有:


xi(k))-ci(k)(xi(k)-PYi(k)(xi(k)))]T=
τij)-xi(k))-hi(k)Tci(k)(xi(k)-
PYi(k)(xi(k)))=
hi(k)Tci(k)xi(k)+hi(k)Tci(k)PYi(k)(xi(k))=
hi(k)Tci(k)PYi(k)(xi(k))
(3)
假设1:在kT时刻,通信拓扑图的并集中任意跟随者与领导者之间至少存在一条有向的路径。
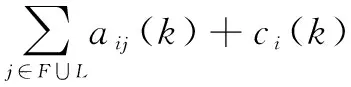
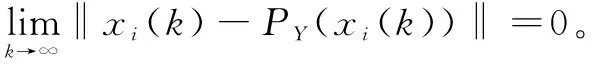
(4)
根据式(3)和引理1可得:
(5)
因为Yi(k)⊆Y,所以PYi(k)(xi(k))=PY(PYi(k)(xi(k)))。
‖xi(k+1)-PY(xi(k+1))‖≤
hi(k)Tci(k)V(k)+hi(k)Tci(k)≤
(1-hi(k)ci(k)T)V(k)
(6)
由假设2可得0≤(1-hi(k)ci(k)T)≤1,即V(k)≤V(k+1)=‖xi(k+1)-PY(xi(k+1))‖,可得出V(k)为单调非增,即跟随者到凸区域Y的最大距离不会增大。为了最终能实现包含控制,必须证明V(k)会随时间减小,下面分两步来证明。
第一步:对于任意跟随者i∈F,当k≤κ且0≤ζ1<1时,如果有‖xi(κ)-PY(xi(κ))‖≤ζ1V(k),那么对于0≤ζ2<1,有‖xi(κ+1)-PY(xi(κ+1))‖≤ζ2V(k)。
根据公式(6)有:
‖xi(κ+1)-PY(xi(κ+1))‖≤
ci(κ)))](1-ζ1)V(k)≤[1-(1-
ΨmaxT)](1-ζ1)V(k)
(7)
根据假设2和式(7)可推导出‖xi(κ+1)-PY(xi(κ+1))‖≤ζ2V(k),此时ζ2=1-(1-ΨmaxT)(1-ζ1)。
第二步:对于任意跟随者iz∈F,设iz能接收到iw∈F∪L的信息,即aiziw(κ)>0,有aiziw(κ)≥λ;ciz(κ)>0,有ciz(κ)≥λ。当k≤κ时,如果有‖xiw(κ-τiziw)-PY(xiw(κ-τiziw))‖≤ζ1V(k),那么有‖xiz(κ+1)-PY(xiz(κ+1))‖≤ζ2V(k),此时0≤ζ1<1,0≤ζ2<1。
证明过程如下:
‖xiz(κ+1)-PY(xiz(κ+1))‖≤
aiziw(κ)TV(k)-aiziw(κ)T(1-ζ1)V(k)≤
[1-hiz(κ)Tciz(κ)]V(k)-aiziw(κ)T(1-
ζ1)V(k)≤(1-aiziw(κ)T(1-ζ1))V(k)≤
(1-λT(1-ζ1))V(k)
(8)
由式(8)可得‖xiz(κ+1)-PY(xiz(κ+1))‖≤ζ2V(k),此时ζ2=1-λT(1-ζ1),很显然0<ζ2<1。
根据假设1至少存在一个跟随者if1∈F在kT时刻能接收到领导者的消息,即ci(k)≥λ。由第二步可得‖xif1(k+1)-PY(xif1(k+1))‖<ζif1V(k),通过第一步运用递归法则可得,对于任意S≥1有ζif1,SV(k)>‖xif1(k+S+1)-PY(xif1(k+S+1))‖,此时0<ζif1,S<1。
同理,存在一个跟随者if2,f2≠f1在(k+1+τif1if2)T时刻能接收到if1或者部分领导者的消息。根据第二步可得‖xif2(k+τif1if2+1)-PY(xif2(k+τif1if2+1))‖<ζif2,1V(k),此时0<ζf2,1<1。通过使用递归法则可得,‖xif2(k+τif1if2+1+S)-PY(xif2(k+τif1if2+1+S))‖<ζif2,S+1V(k),此时0<ζif2,S+1<1、S≥1。

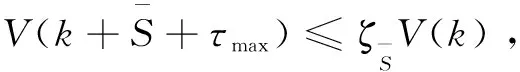
4 数值仿真
为了证明控制算法的有效性,本节通过两次仿真案例对设计的算法进行验证。在第一次仿真中考虑由6个智能体n1,n2,…,n6和4个领导者m1,m2,m3,m4构成的多智能体系统,其通信拓扑如图2所示(多智能体系统通信拓扑1),由三个拓扑结构G1,G2,G3组成,在系统运行过程中每隔1秒切换一次拓扑,显然G1∪G2∪G3满足假设1的条件。令aij(k)=1.5,ci(k)=0.23,采样周期T=0.2,显然满足假设2的条件。

图2 多智能体系统通信拓扑1
将所有跟随者的输入约束范围设置为由半圆x2+(y-0.75)2=0.75(y≥0.75)、x2+(y+0.75)2=0.75(y≤-0.75)与四条线段y=-x+1.5(0.75
第二次仿真采用的通信拓扑如图5所示(多智能体系统通信拓扑2),三个拓扑结构对应的通信时滞为0.1 s,0.2 s,0.3 s。仿真结果如图6、7所示,假设多智能体系统包括n1,n2,…,n6等6个跟随者和L1,L2,L3,L4等4个领导者。通信拓扑按照Ga,Gb,Gc顺序依次切换,每个拓扑的持续时间为1 s,显然Ga∪Gb∪Gc满足假设1的条件。假设三个拓扑结构中智能体间的通信时滞分别为0.1 s,0.2 s,0.3 s。

图3 跟随者输入约束1 图4 跟随者运动轨迹1

图5 多智能体系统通信拓扑2
令aij(k)=0.12,ci(k)=0.1,采样周期T=0.2,显然能使假设2满足。4个领导者的初始位置为:L1:(-1,1),L2:(1,1),L3:(-1,-1),L4:(1,-1)。6个跟随者的初始位置分别为:n1:(-3,3),n2:(0,3),n3:(3,3)n4:(-3,-3),n5:(0,-3),n6:(3,-3)。将所有跟随者的输入约束范围设置为:半圆(x-0.5)2+y2=0.5(x≥0.5)、(x+0.5)2+y2=0.5(x≤-0.5)与四条线段y=-x+1(0

图6 跟随者输入约束2 图7 跟随者运动轨迹2
5 结束语
该文研究了受输入约束的多智能体系统包含控制问题,考虑了跟随者受通信时滞影响,同时该系统通信拓扑为有向切换的。针对该问题设计了一种基于邻居位置信息以及投影的包含控制算法,将跟随者与凸区域的距离构建为李雅普诺夫函数,运用凸分析、模型转换等方法首先证明了领导者与凸区域的距离不会随时间变化增大,接着证明了所有能与领导者直接或间接通信的跟随者与凸区域间的距离随时间变化减小,最终所有跟随者与凸区域间的距离收敛到0,即所有控制输入受约束的跟随者均能进入到由领导者构成的凸区域中。最后通过数值仿真证明了理论结果的正确性。文中考虑的系统为一阶采样系统,下一步工作将探究受输入约束和时延影响的二阶采样多智能体系统包含控制问题以及动态领导者的情况。
