一道竞赛试题的多角度探索
2022-04-01彭光焰
彭光焰
(湖北省广水市一中 432700)
1 一道赛题
题目(2012年上海市高中数学竞赛试题第9题)如图1,ABCD中,AB=x,BC=1, 对角线AC与BD的夹角∠BOC=45°,记直线AB与CD的距离为h(x).求h(x)的表达式,并写出x的取值范围.

图1
此题短小精悍,内涵十分丰富,解法多样,命题者真是匠心独运,是值得研究的一道好题,下面给出本题的多种解法,其中解法7是命题者给出的参考答案,解法11是文[1]所给的,剩余10种解法是笔者给出的.
2 解法探析
2.1 利用解直角三角形
解法1作DF⊥AB于点F,CE⊥AB于点E,如图2,设DF=CE=t.

图2

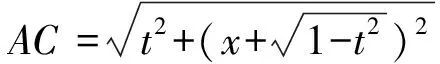

而S=tx=4S△BOC,
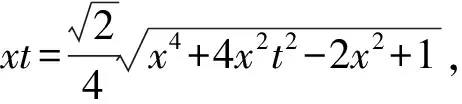
4x2t2=(x2-1)2,
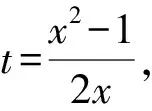
解法2 如图3,过点B作BE⊥AC于点E,过点D作DF⊥AB于点F,则ΔBEO为直角三角形.

图3
设OE=BE=m,EC=n
因为BC=1,所以m2+n2=1.
在Rt△ABE中,
AE=AO+OE=2m+n,
x2=AB2
=AE2+BE2
=(2m+n)2+m2
=4m2+4mn+(m2+n2)
=4m2+4mn+1,

又S=2S△ABC,

DF·x=m(2m+2n),

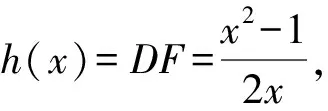
解法3 如图3,设AC=2a,BD=2b,


在Rt△ABE和RtΔBCE中,由勾股定理,得
①
②
③
又S=xh(x),
S=2S△ABC
=AC×BE

④
2.2 利用两角和的三角函数
解法4如图2,设∠CAB=β,∠ABD=α,则α+β=45°.
设BE=y,CE=n,
则AF=BE=y,DF=CE=n.



⑤
在Rt△BCE中,n2+y2=1,
即y2=1-n2.
⑥

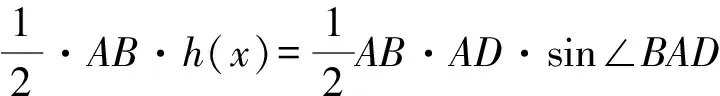
即x2-2x-1≤0,
而h(x)>0,
即x2-1>0,x>1,x<-1.

2.3 利用余弦定理
解法5 如图2,设AC=2a,BD=2b,则OC=a,OB=b,并设h(x)=t.
在△BOC中,由余弦定理,得

⑦
在Rt△ACE和Rt△BDF中,由勾股定理得,
⑧

⑨
⑩
因为S=xt,

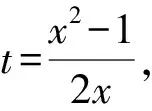

而0 解法6 由解法5所设,在△BOC和△AOB中,分别由余弦定理可得, 又S=4S△BOC, 解法7 由平行四边形对角线平方和等于四条边的平方和得 在△OBC中,由余弦定理,得 BC2=OB2+OC2-2OB·OCcos∠BOC, S=4S△OBC 解法8 如图4,设AO=OC=a,BO=OD=b,h(x)=t. 图4 在Rt△BEO中,∠BOC=45°, 在△BOC和△AOB中由余弦定理,得 又因为 S=h(x)·x, 解法10 如图5,以点A为原点,AB所在直线为x轴建立平面直角坐标系.于是B(x,0). 图5 又AD=BC=1,故m2+n2=1. 解法11 如图4所示的平面直角坐标系,于是B(x,0),然后利用直线的到角公式来求解. 设∠DAB=θ(0<θ<π), 于是D(cosθ,sinθ),C(cosθ+x,sinθ),h(x)=sinθ. 再设AC,BD所在直线的斜率分别为k1,k2,且k1,k2均存在. 根据到角公式, 将k1,k2代入上式, 解法12 建立如图6所示平面直角坐标系. 由已知条件可知,可设(a,a),B(b,0),则A(-a,-a). 图6 由两点式可得直线AB的方程为 ax-(a+b)y-ab=0. 则h(x)就是点C到直线AB的距离,即 又|AB|2=x2, 即x2=(a+b)2+a2, |BC|2=12, 即1=(a-b)+a2, x2-1=4ab.


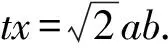
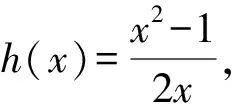

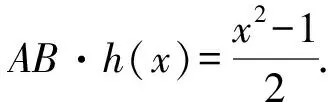


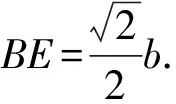


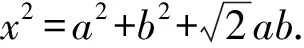

2.4 利用平面向量
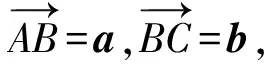
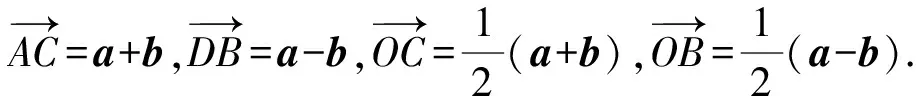



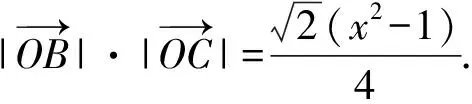

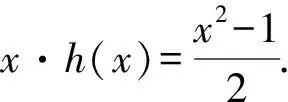
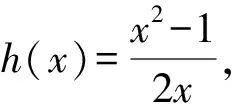






2.5 利用平面解几何




