高中化学中晶体相关计算的归纳

张 冉

(四川省成都市锦江区嘉祥外国语高级中学 610011)

晶体中的相关计算是近年来高考热点之一，该部分注重考查学生的空间想象能力和计算能力，此类题目难度较大，综合性较强，有较好的区别度.但是在高中化学《选修3》教材中并没有涉及与之相关的过多介绍，故不少学生觉得学起来抽象，难突破，甚至一些一线教师也难找到切实可行的教学方法让学生轻松解决此类题型.结合教学实践以及对近几年的高考题的研究发现，这类题型主要是根据晶胞确定晶体的组成并进行粒子数、配位数、密度、质点距离、质量、阿伏加德罗常数、空间利用率等相关计算.现将有关内容概括如下，供参考.

1 利用均摊法推求晶胞中原子个数、晶体的化学式

图1

晶胞为平行六面体且具有无隙并置的结构特点，故顶点原子对晶胞的贡献为1/8，面上1/2，棱上1/4，体内1.如图1所示，A原子的个数为6×1/2=3，B原子的个数为1，C原子的个数为8×1/8=1，所以该晶体的化学式为A3BC.

2 根据晶胞结构判断配位数

图2

3 晶胞密度的计算

若题干上已知晶胞密度，也可根据此公式计算出晶胞边长.

4 晶体中原子的空间利用率的计算

原子的空间利用率是按一个晶胞来定义的：

教材在金属晶体这部分有所涉及，所以显得尤为重要.金属晶体的堆积模型有四种基本形式—简单立方堆积、体心立方堆积、六方最密堆积、面心立方最密堆积.计算空间利用率的关键是要先确定金属原子在堆积时，在立方体的哪个部位金属原子(小球)是相互接触，可借助模型直观感受，也可通过立体几何论证.

4.1 简单立方堆积

此类晶胞在结构上的特点是边上的两个小球相切，若设晶胞边长为a，小球半径为r，则a=2r.简单立方晶胞中金属原子数为1，立方体体积为a3，由此可得出简单立方堆积空间利用率为：

4.2 体心立方堆积

4.3 六方最密堆积

图4

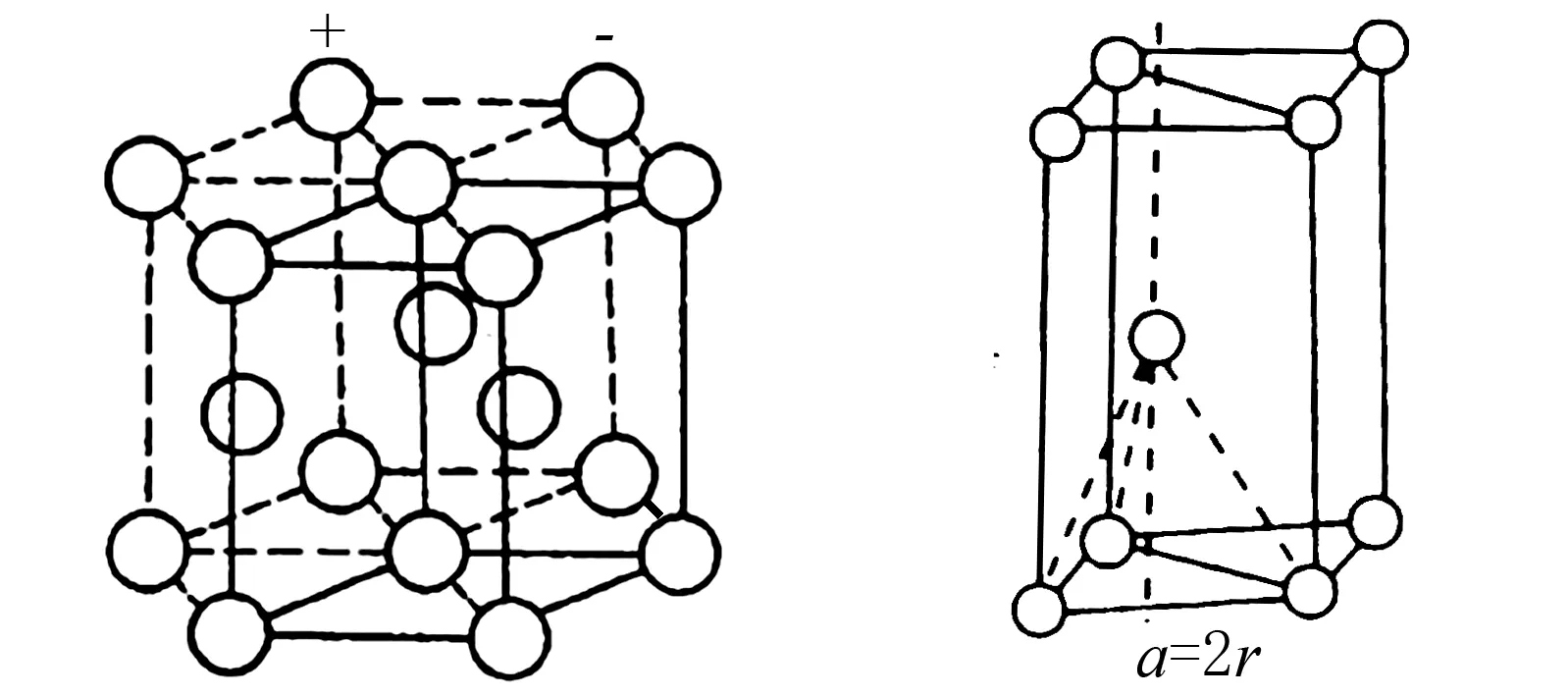
图5

4.4 面心立方最密堆积

图6

5 计算晶胞中两原子之间的距离

晶胞中若两原子间已形成化学键，则此距离为化学键键长，以金刚石晶胞为例.

图7

又如干冰晶胞，CO2分子采取密堆积，占据8个顶点和6个面心，故最近且相邻的CO2间的距离为面对角线的1/2.

6 分子晶体中键的数目、多面体的计算

已知C60是由60个碳原子形成的分子，形似足球，又叫足球烯.一类题型是问1mol C60与足量的F2反应的产物，要解决该问题就得清楚C60中碳碳单键和双键的数目.C60的球形是由多个五边形和六边形组成，每个碳原子连3条边，结合碳原子4个价电子形成四根键即每个碳原子形成1个双键和2个单键，而每根键又被2个碳原子共用，故60个碳共形成60×1.5根键，双键与单键个数比为1∶2，得到C60中有30根双键和60根单键，所以产物应该为C60F60.还可以继续求算五边形和六边形的个数.根据欧拉定律面+顶点-棱=2，设五边形、六边形个数分别为x、y，列式(x+y)+(5x+6y)/3+(5x+6y)/2=2可计算出五边形、六边形各有12、20个.同样的方法可以计算C70、B12.

除上述总结之外，还可根据晶胞中原子的位置(原子坐标)来解决原子之间距离.通常用xa+yb+zc中的x,y,z组成的三数组来表达晶胞中原子的位置，称为原子坐标.例如，位于晶胞原点(顶角)的原子的坐标为0,0,0；位于晶胞体心的原子坐标为1/2，1/2，1/2；位于面心的原子坐标为1/2，1/2，0；1/2，0，1/2；0,1/2,1/2等等.原子坐标绝对值的取值区间为1>|x(y，z)|≥0.若取值为1，相当于平移到了另一个晶胞，与取值为零毫无差别，简言之1即是0.例如，金刚石晶胞中有8个原子，它们的原子坐标分别是0,0,0(顶角原子)；1/2，1/2，0；1/2，0，1/2；0，1/2，1/2(三个面心原子)；3/4，1/4，1/4；1/4，3/4，1/4；1/4，1/4，3/4和3/4，3/4，3/4(4个分处晶胞体对角的1/4处)，也可分析出最近的2个碳原子间距离.